Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы
Подождите немного. Документ загружается.


меренным величинам. Так как в триангуляции измеряются на-
правления, то триангуляционные сети следует уравнивать по на-
правлениям, Однако на практике нередко вместо направлений
уравнивают углы, которые находятся как разности направлений
и поэтому являются величинами зависимыми. В процессе уравни-
тельных вычислений эта зависимость не учитывается, вследствие
чего возникают некоторые искажения уравненных элементов сети
и особенно результатов оценки точности.
При уравнивании геодезических сетей коррелатным способом
существенное значение имеет правильное определение числа и ви-
да независимых условных уравнений. Не должно быть ни пропу-
щенных независимых условных уравнений, ни избыточных сверх
необходимого числа их. При включении избыточного, т. е. зависи-
мого условного, уравнения, являющегося линейной комбинацией
независимых условных уравнений, будет -получена неразрушимая
система нормальных уравнений, определитель которой равен нулю.
С другой стороны, если какое-либо условное уравнение будет про-
пущено, то цель уравнивания не будет достигнута, так как соот-
ветствующая данному условию невязка не будет устранена. Поэто-
му правильный выбор независимых условных уравнений в геодези-
ческой сети и безошибочное определение их числа, в том числе но
видам, имеет принципиальное значение.
§ 36. Число и виды независимых условных уравнений
В свободной сети триангуляции с одной исходной стороной и ее
азимутом могут возникать следующие виды условных уравнений:
фигур, горизонта — при уравнивании углов, а не направлений, по-
люсные и проекций. Условия проекций появляются в том случае,
когда длинные диагонали соединяют пункты, разделенные рядом
треугольников, не имеющих общей вершины. Такие построения с
длинными диагоналями в настоящее время не применяются в гео-
дезическом производстве. Поэтому условия проекций рассматри-
ваться в дальнейшем не будут.
Если в свободной сети есть дополнительно измеренные стороны
и азимуты, кроме исходных, то в такой сети появятся еще условия
базисные и дирекционных углов (азимутальные).
Общее число независимых условных уравнений в геодезичес-
кой сети равно числу избыточно измеренных в ней величин: на-
правлений (углов), азимутов (дирекционных углов) и длин сторон.
Число избыточно измеренных величин определяется как разность
числа всех измеренных величин и числа необходимых для ее по-
строения измеренных величин. Имея это в виду, приведем свод-
ку формул для определения числа и вида независимых уравнений,
возникающих в свободной триангуляции для случая измерения и
уравнивания направлений:
S
H
= D*-(2k + t); /
e
D-/-p+ 1; с = р —2п + 3;
г
б — k
6
— 1; г
д
= k
A
—
1,
где D* *=D + k
a
+ ka.
(8.1)
(8.2)
109
При уравнивании сети по углам число независимых условных
уравнений определяется по формулам
S
y
= N*—2k; f = N —р —
<7
+
1;
q=N+t— D;
с = р — 2п + 3;
где N* =N + k
s
+ kа.
re =
^б
—
1
;
г
д =
^д — I >
(8.3)
(8.4)
В формулах (8.1) — (8.4) приняты обозначения: S
H
и S
y
— об-
щее число независимых условных уравнений в сети при уравнива-
нии ее по направлениям и углам соответственно; f — число услов-
ных уравнений фигур; q — число условий горизонта; с — число по-
люсных (боковых) условий;
Гб
— число базисных условий; г
д
—
число условий дирекционных углов; D* — число измеренных в сети
направлений Z), сторон k
s
и азимутов вместе взятых (подчерк-
нем, измеренных, но не вычисленных по координатам исходных
пунктов); N* — число измеренных в сети углов N, сторон k
s
и ази-
мутов k
a
, вместе взятых; kб — общее число исходных и дополни-
тельно измеренных сторон; — общее число исходных и дополни-
тельно измеренных азимутов (дирекционных углов); п — число
всех пунктов в сети (исходных и определяемых); k — число опре-
деляемых пунктов; р — число всех сторон в сети (исходных и оп-
ределяемых); t — число пунктов, на которых исполнены угловые
измерения.
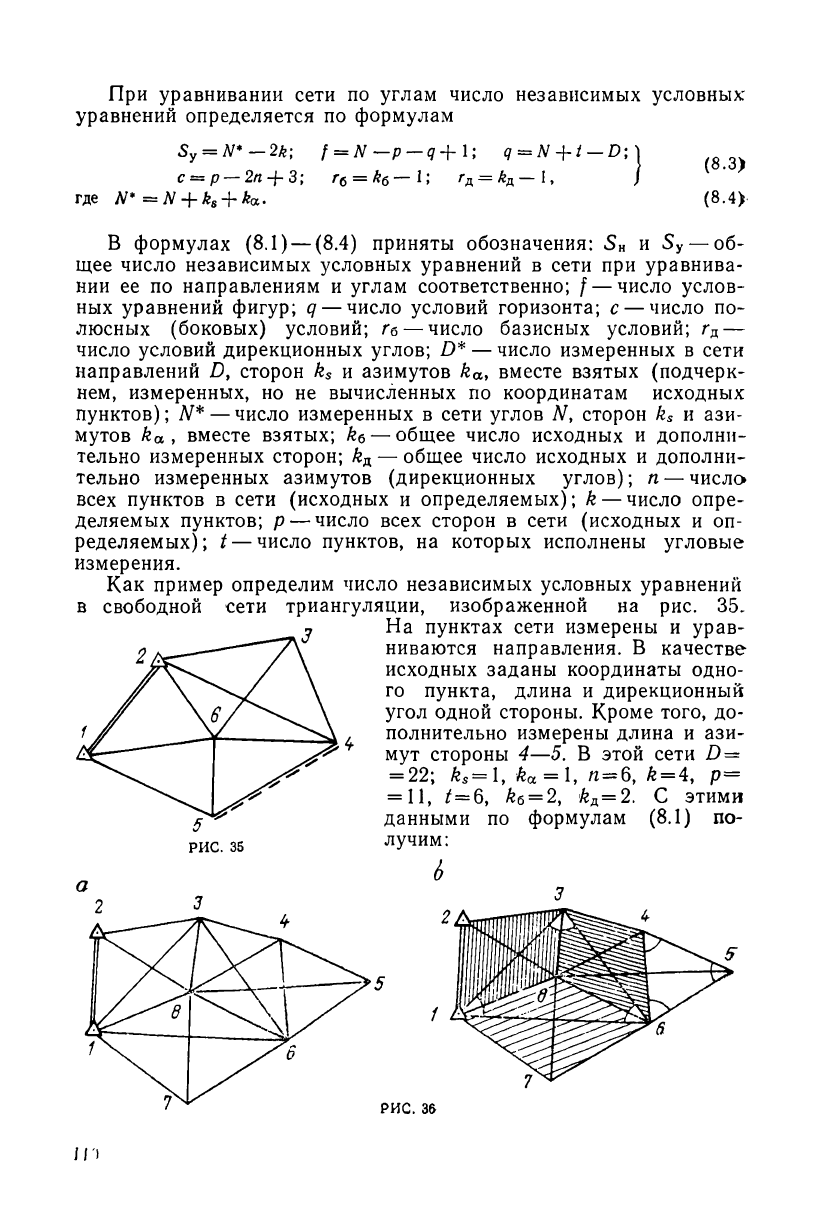
Как пример определим число независимых условных уравнений
в свободной сети триангуляции, изображенной на рис. 35.
На пунктах сети измерены и урав-
ниваются направления. В качестве
исходных заданы координаты одно-
го пункта, длина и дирекционный
угол одной стороны. Кроме того, до-
полнительно измерены длина и ази-
мут стороны 4—5. В этой сети D =
= 22; k
s
= 1, k
a
= 1,
/г
=
6,
6 =
4,
р=
= 11, / = 6, £
б
= 2,
&
д
= 2. С этими
данными по формулам (8.1) по-
лучим:
ь
РИС. 35
111

всего условий S
H
= D*—(2k + t) = 24-(8 + 6) = 10;
фигур f = D—t—p+
1
= 22—6—11 +
1
= 6;
полюсных с—р—2/2 + 3=
11
—12 +
3
= 2;
базисных Гб=Лб—1=2—1 = 1;
дирекционных углов —
1
=
2—1
= 1.
В более сложной сети, изображенной на рис. 36 и уравнивае-
мой по углам, имеем N = 29, k
s
=
0
y
ft
a
=0, n = t = 8,
&
= 6, р=18,
й
6
=1, /5
Д
=1; в этой сети 36 направлений, образующих измерен-
ные углы (D = 36). С этими данными получим по формулам (8.3)
следующее число независимых условных уравнений: всего —17, из
них фигур —11, горизонта —1, полюсных —5.
При выборе фигур для составления независимых условных
уравнений целесообразно иметь в виду следующие соображения.
Условные уравнения горизонта возникают при уравнении сети
только по углам; число их равно числу полюсов центральных сис-
тем, на которых измерены углы или направления. Так, например,
в сети, изображенной на рис. 36, а, возникает одно условное урав-
нение горизонта на пункте 8, что согласуется с расчетами по фор-
мулам (8.3).
Полюсные условия возникают только в геодезических четырех-
угольниках и центральных системах, которые легко опознаются
на схеме сети. Число полюсных условий равно числу геодезических
четырехугольников и числу полюсов центральных систем, вместе
взятых.
Если при каком-либо полюсе окажется ряд центральных систем
с разным числом треугольников в каждой из них, то для составле-
ния независимого полюсного условия берут только одну систему
(по числу полюсов) с наименьшим числом треугольников в ней.
В этом случае число вычислительных операций будет меньше, чем
при выборе центральной системы с наибольшим числом треуголь-
ников, а конечный результат уравнивания будет один и тот же.
В сети на рис. 36,6 независимые полюсные условия возникают
во всех геодезических четырехугольниках: 8123, 8346, 8456, 8671 и
одной центральной системе 8136 с полюсом на пункте 8. Всего
пять полюсных условий, что и должно быть согласно расчетам по
формулам (8.3).
Выбор независимых условий фигур особенно в сложных сетях с
большим числом диагоналей требует применения особых приемов,
не только обеспечивающих, но и контролирующих правильность
решения этой задачи. Один из таких приемов графического реше-
ния задачи приведен в книге Б. Н. Рабиновича*. Рассмотрим спо-
соб графического контроля выбора независимых условий фигур.
1. На схеме сети выделяют штриховкой все неперекрывающие-
ся между собой геодезические четырехугольники.
2. В каждом из этих четырехугольников берут по три любых
треугольника и для них составляют независимые условия фигур.
* Практикум по высшей геодезии. М., Геодезиздат, 1961.
111

3. Со схемы сети выписывают все оставшиеся треугольники, в
которых ни один из углов не входит в какой-либо заштрихован-
ный геодезический четырехугольник, и для этих треугольников
составляют оставшиеся независимые условия фигур.
Данный способ выбора независимых условий фигур рассмот-
рим на примере сети, изображенной на рис. 36, б, в которой воз-
никает 11 независимых условий фигур. Выделим штриховкой все
неперекрывающиеся геодезические четырехугольники, например
8123, 8346, 8671, и в каждом из них возьмем по три треугольни-
ка: 813, 812, 823; 836, 834, 846\ 861, 867, 871 — всего 9 треуголь-
ников. Внимательно просмотрев схему сети, найдем два треуголь-
ника 456 и 136, в которых ни один из углов не входит в какой-
либо заштрихованный геодезический четырехугольник. Итак, мы
выбрали 11 треугольников для составления 11 независимых усло-
вий фигур.
Для составления базисного и азимутального условных уравне-
ний выделяется в сети цепочка треугольников по кратчайшему пу-
ти между соседними базисными сторонами и исходными дирекци-
онными углами соответственно. Число базисных условий на едини-
цу меньше числа базисных сторон; число азимутальных условий
на единицу меньше числа исходных дирекционных углов в сети.
Перейдем к определению числа и вида независимых условных
уравнений в сети триангуляции, изображенной на рис. 31, которую
будем уравнивать коррелатным способом по направлениям. В этой
сети пять пунктов (я=5), из которых два исходных и три опреде-
ляемых
(i&
= 3); число всех сторон девять (р = 9); горизонтальные
направления в количестве восемнадцати (Z)=18) измерены на всех
пунктах (^=5); дополнительно измеренных сторон и азимутов нет
= В данной сети при уравнивании направлений возни-
кают условные уравнения только фигур и полюсные, число кото-
рых определим по формулам (8.1):
всего условий S
n
= D—(2k + t) = 18—6—5 = 7;
фигур /=D—t—р +1 = 18—5—9 +1=5;
полюсных с=р—2п + 3 = 9—10 + 3 = 2.
§ 37. Составление условных уравнений
и функций уравненных элементов
Условия фигур. Составление независимых условных уравнений
начинается с условий фигур. Для уравниваемой сети (см. рис. 31)
приведены в табл. 38 значения измеренных углов в треугольниках,
их невязки. Независимые условные уравнения фигур записаны в
последнем столбце этой таблицы. Неизвестными в условных урав-
нениях фигур являются поправки к направлениям. Номера и зна-
ки этих поправок легко определить по графе «разность направле-
ний». При уравнивании сети по направлениям в каждом условном
уравнении сумма коэффициентов при поправках к направлениям
должна быть равна нулю, что следует использовать как контроль
при составлении условных уравнений.
112
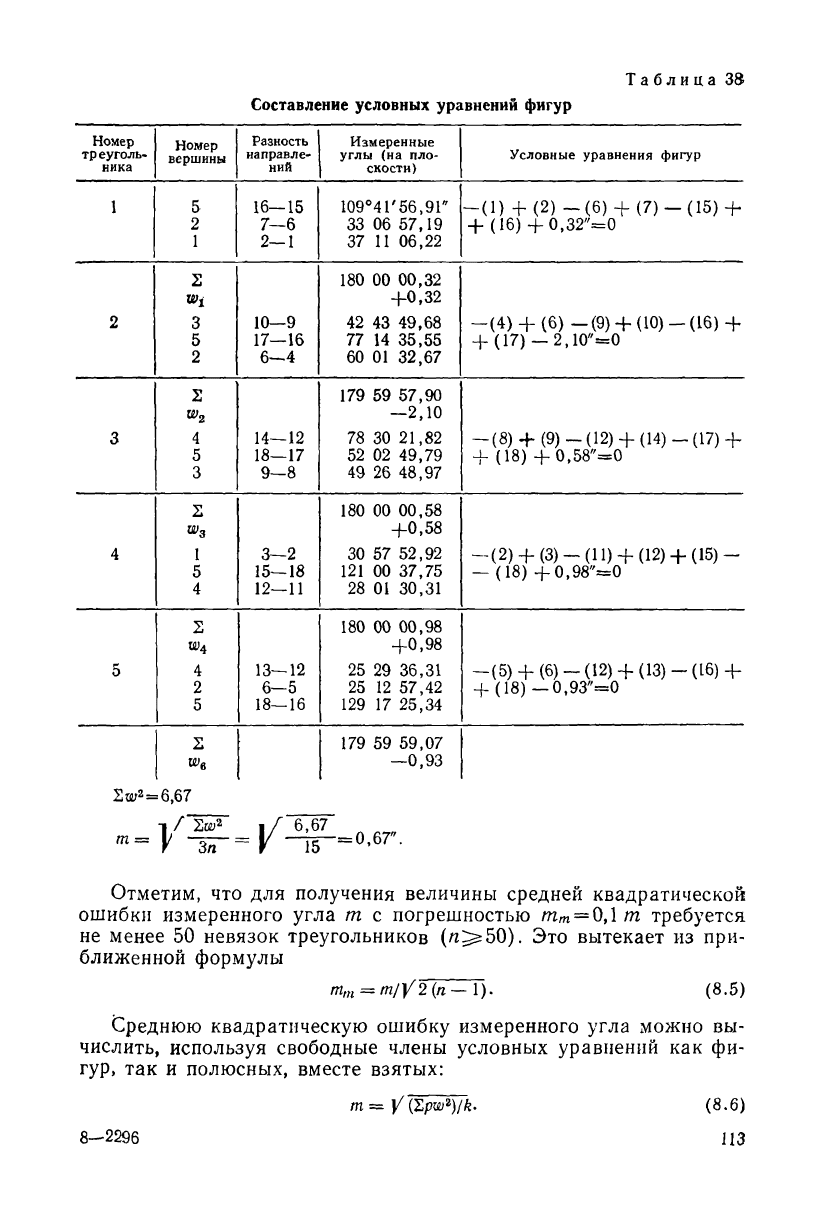
Таблица 38
Составление условных уравнений фигур
Номер
треуголь-
ника
Номер
вершины
Разность
направле-
ний
Измеренные
углы (на пло-
скости)
Условные уравнения фигур
1
5
2
1
16-15
7-6
2-1
109
о
4Г56,9Г
33 06 57,19
37 11 06,22
-(1)+(2)-(6)+ (7)-(15) +
+ (16) +0,32"=0
2
Wi
180 00 00,32
+0,32
2
3
5
2
10—9
17—16
6—4
42 43 49,68
77 14 35,55
60 01 32,67
_
(4
) + (6)-(9) + (10)-(16) +
+ (17) — 2,10"=0
Щ
179 59 57,90
—2,10
3
4
5
3
14—12
18-17
9-8
78 30 21,82
52 02 49,79
49 26 48,97
-(8)+ (9)-(12)+ (14)-(17) +
+ (18) + 0,58"=0
2
Щ
180 00 00,58
+0,58
4
1
5
4
3—2
15—18
12—11
30 57 52,92
121 00 37,75
28 01 30,31
— (2) + (3) — (11) + (12) + (15) —
— (18) + 0,98"=0
2
w
4
180 00 00,98
+0,98
5
4
2
5
13—12
6-5
18—16
25 29 36,31
25 12 57,42
129 17 25,34
—(5) + (6) — (12) + (13)
—
(16) +
+ (18) — 0,93"=0
2
Щ
179 59 59,07
—0,93
2ш
2
= 6,67
Отметим, что для получения величины средней квадратической
ошибки измеренного угла т с погрешностью m
m
=
0,1
т требуется
не менее 50 невязок треугольников Это вытекает из при-
ближенной формулы
т
П1
=
т
/У2(п — 1). (8.5)
Среднюю квадратическую ошибку измеренного угла можно вы-
числить, используя свободные члены условных уравнений как фи-
гур, так и полюсных, вместе взятых:
8—2296
т = У
(Zpw*)/k.
(8.6)
113

В этой формуле квадраты невязок треугольников умножаются
яа. р= 7з, а квадраты свободных членов полюсных условий на р =
= ; k — число свободных членов условных уравнений фигур
и полюсных, вместе взятых; 2ctg
2
p— сумма квадратов коэффи-
циентов соответствующего полюсного условного уравнения.
В рассматриваемой сети
&
= 7 (в ней 5 условий фигур и 2 по-
люсных). С учетом данных, приведенных в табл. 38, 39 и 40, по-
лучим
V
я
и/
"Т
6,67
^ "ГэТзГ
2
>
3Q2
+ "7Y7Y9~
q
>44
2
т= |/
!
=
!
= 0,60".
Полюсные условия. В нашей сети возникает два полюсных ус-
ловия: в геодезическом четырехугольнике с вершинами 2345 и
центральной системе 5124 (см. рис. 37 и 38). В геодезическом че-
тырехугольнике за полюс принимают либо вершину с наиболее
тупым углом, либо точку пересечения диагоналей. В этом случае
коэффициенты полюсного условного уравнения будут иметь наи-
большие по величине значения, благодаря чему неизвестные по-
правки направлений определятся с большей точностью, чем при
выборе полюса в другой точке.
Обозначив через (3/ и (3/ связующие углы соответственно числи-
теля и знаменателя дроби полюсного условия, а через П] и Пг —
соответственно произведения синусов измеренных значений этих
углов, напишем полюсное условное уравнение в линейном виде
2 ctgр, (Р
й
) - 2 ctgр,
(р
;
.)
+ w = 0, (8.7)
где w
•
П1-П
2
п,
В случае уравнивания направлений поправки р в углы надо
выразить через разности поправок соответствующих направлений:
поправка правого направления минус поправка левого направле-
ния.
За порядком составления полюсных условных уравнений, вы-
числением их коэффициентов и свободных членов можно просле-
дить по приведенным ниже схемам и таблицам.
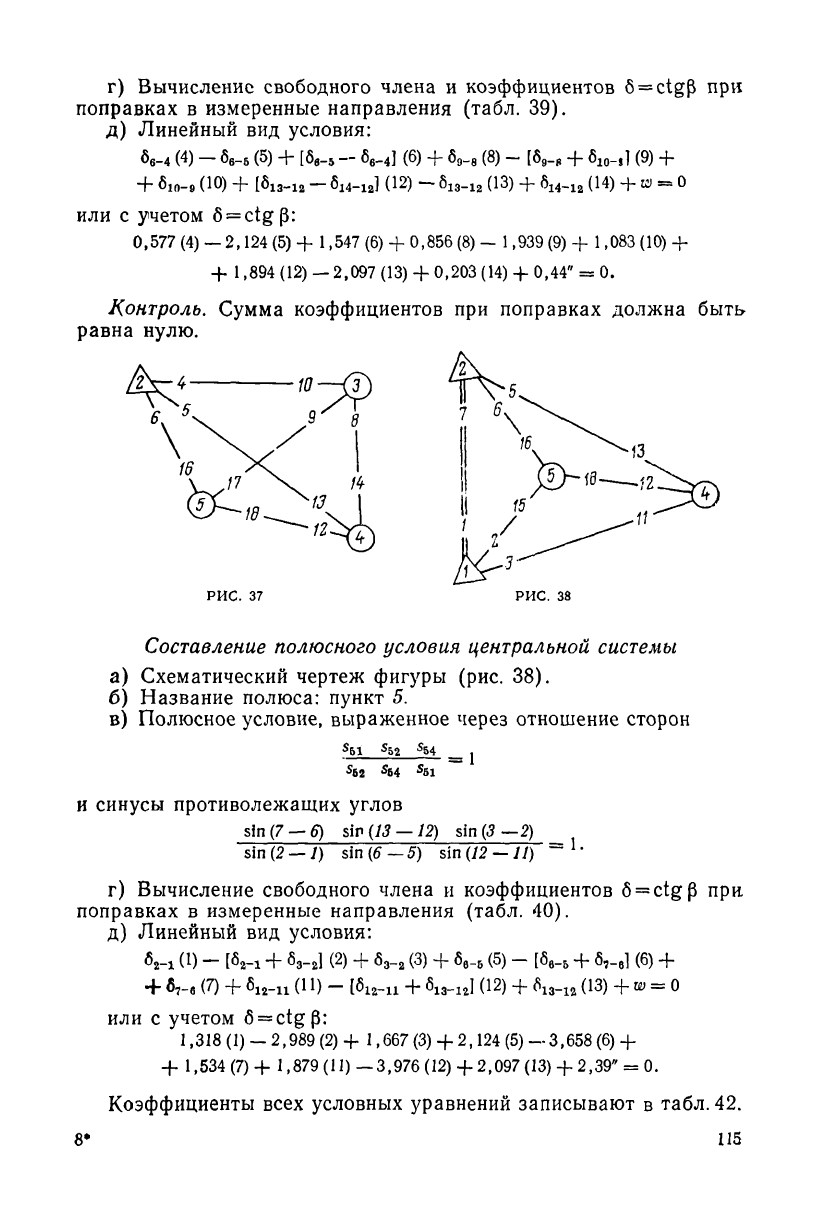
Составление полюсного условия
геодезического четырехугольника
а) Схематический чертеж фигуры (рис. 37).
б) Название полюса: пункт 5.
в) Полюсное условие, выраженное через отношения сторон
^>53
S
54
= 1
s
53
S
54 %2
и синусы противолежащих углов
sin
(10 — 9)
sin
(14
—12) sin
(6 — 5)
_
sin
(6
—
4)
sin
(9
— 8) sin
(13
—
12)
~
1
'
114
г) Вычисление свободного члена и коэффициентов
6
= ctgjJ при
поправках в измеренные направления (табл. 39).
д) Линейный вид условия:
б
б
_
4
(4) - б
6
-
б
(5) + [б
б
_
5
- 6
6
-
4
] (6) + б
9
.
8
(8) - [б
9
.
р
+ 6
10
_,1 (9) +
+ 6
10
_
9
(10) + [6
13
-
12
- б
14
-
12
] (12) - б
13
.
12
(13) + 6
14
_
12
(14) + w - о
или с учетом
6
= ctgp:
0,577 (4) — 2,124 (5) + 1,547 (6) + 0,856 (8) — 1,939 (9) + 1,083 (10) +
Контроль. Сумма коэффициентов при поправках должна быть
равна нулю.
Составление полюсного условия центральной системы
а) Схематический чертеж фигуры (рис. 38).
б) Название полюса: пункт 5.
в) Полюсное условие, выраженное через отношение сторон
г) Вычисление свободного члена и коэффициентов
б
= ctg р при
поправках в измеренные направления (табл. 40).
д) Линейный вид условия:
в
м
(1) - [в
м
+ 6
3
-
2
] (2) + б
3
-
2
(3)
+ б
6
_
6
(5)
- [6
в
_
5
+ 6,.
б
] (6) +
+ Ve (7) + 6
12
_
u
(11) - [6
12
-
и
+ 6
13
_
12
] (12) + (13) +
ш
= 0
или с учетом б = ctg р:
1,318 (1) - 2,989 (2) + 1,667 (3) + 2,124 (5) —3,658 (6) +
+ 1,534 (7) + 1,879 (II)
—
3,976 (12) + 2,097 (13) + 2,39" = 0.
Коэффициенты всех условных уравнений записывают в табл. 42.
8* 115
+ 1,894 (12) — 2,097 (13) + 0,203 (14) + 0,44" = 0.
РИС. 37
РИС. 38
s
bl
s
52
S
54
$62 *64
5
S1
и синусы противолежащих углов
sin
(7
—
6)
siv
{13
—12) sin (3—2)
sin
(2 — 1)
sin (6 —
5)
sin
(12
—
11)
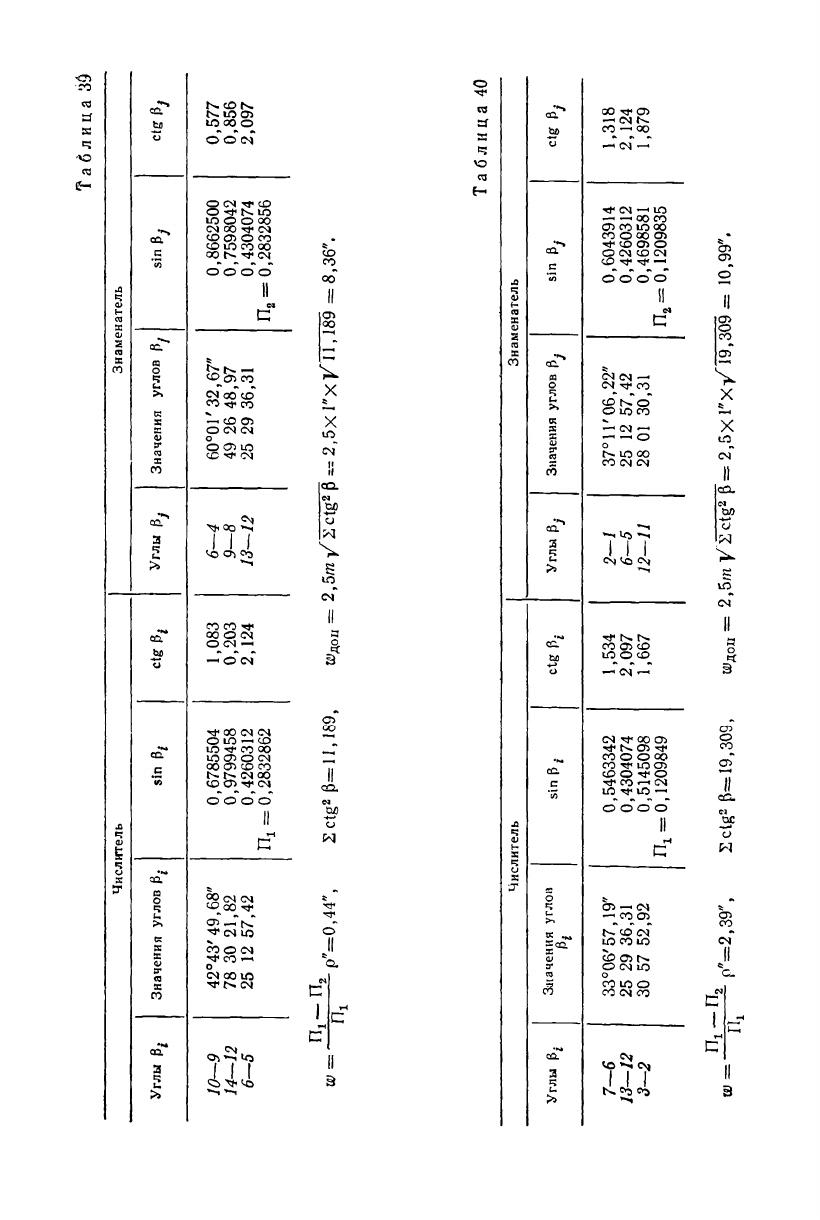
Таблица 3$
Числитель
Знаменатель
Углы
Значения углов 0.
sin f3j
ctg
Углы f5j
Значения углов f^
sin
cter|?
y
10—9
14—12
6—5
42°43'49,68"
78 30 21,82
25 12 57,42
0,6785504
0,9799458
0,4260312
U
x
= 0,2832862
1,083
0,203
2,124
6—4
9—8
13—12
60°01'32,67"
49 26 48,97
25 29 36,31
0,8662500
0,7598042
0,4304074
П
2
= 0,2832856
0,577
0,856
2,097
Пг
р"=0,44», 2 ctg
2
1J, 189, ^
Д
ои= 2,5т /2 ctg
2
0 « 2,5х l"x/i 1,189 = 8,36*.
Таблица 40
Числитель
Знаменатель
Углы
Значения углои
h
sin
ctg 0.
Углы Значения углов 0^
sin Эу
ctg fy
7—6
13—12
3—2
33°06' 57,19"
25 29 36,31
30 57 52,92
0,5463342
0,4304074
0,5145098
П
1 =
0,1209849
1,534
2,097
1,667
2—1
6—5
12—11
37°1Г 06,22"
25 12 57,42
28 01 30,31
0,6043914
0,4260312
0,4698581
П
2
= 0,1209835
1,318
2,124
1,879
П1
п
П2
р"=2,39", 2ctg
2
Р=19,309, ш
до11
= 2,5т/2ctg
2
Р=2,5х1"х/19,309 = 10,99".

Составление весовой функции
Пусть в уравненной сети требуется определить среднюю квад-
ратическую ошибку длины наиболее удаленной стороны s
34
. Для
этого надо вычислить обратный вес этой стороны. С этой целью
длину стороны s
34
представим как функцию уравненных направле-
ний, идя от исходной стороны 5i2 по кратчайшему пути через два
треугольника 124 и 234:
__ sin
(3 — 1)
sin
(5 — 4)
sin
(13
—11) sin
(10
—
8)
*
Для вычисления обратного веса этой функции найдем ее при-
ращение AF=f
s
. Взяв частные производные от F по каждому из-
меренному направлению и перейдя к конечным приращениям, по-
лучим
h = As
34
« 0) + Vi (3) - Л5-4 № - Л5-4 (5) +
+ AlO-8 (10)4- (11)- (13), (8.8)
где
AA-l=vctg(*-i)=v8A-
f
. (
8
-
9
)
_ %4
ДМ
*12
дм
sin (3-1) sin (5
• 4)
s
12
^ Пх
р" р" sin(13 —11) sin
(10
—8) - р" " П
2
'
В целях удобства вычислений длины сторон Sn и S34 в форму-
ле (8.10) выражают в дециметрах.
Порядок вычисления коэффициентов Ak-i весовой функции f
s
можно проследить по табл. 41.
Таблица 41
а) Вычисление длины стороны s
3
4 и коэффициента v
Числитель
Знаменатель
Углы
(А-0
Значения углов
sin углов
Углы
(b-i)
Значения углов
sin углов
3—1
5—4
68°08'59"
34 48 35
0,928160
0,570853
П
г
= 0,529843
13—11
10—8
53°31' 07"
92 10 39
0,804050
0,999278
П
2
=0,803469
512=122 186 дм,
П, s
34
w*
s
34
=
Sl
o
AM
ТГ =
«О
575 дм, v = =0,3906.
11
2
р
б) Вычисление коэффициентов ctg (k—i)
Углы (ft—i) Значения углов ctg (k-i)
д k-i -v ctg (ft—г)
3—1
68°08' 59"
0,4010
0,157
5—4
34 48 35
1,4384
0,562
13-11
53 31 07 0,7394 0,289
10—8
92 10 39
—0,0380 —0,015
117

С учетом данных, приведенных в табл. 41, весовая функция,
примет окончательный вид
и = As
34
= —0,157 (1) + 0,157 (3) - 0,562 (4) + 0,562 (5) —
— 0,015 (8) + 0,015 (10) + 0,289 (11) — 0,289 (13).
Коэффициенты при поправках направлений весовой функции f
s
записывают в столбец f табл. 42 условных уравнений.
Таблица 42
Таблица коэффициентов условных уравнений
Номер
попра-
вок
р
с
2
С
4
ав
а
7
f
S'
Поправки
V
О)
1
— 1
1,318 —0,157
0,161
—0,10"
(2)
1 1
— 1
—2,985
—2,985 0,41
(3)
1
1
1,667
0,157 2,824
—0,31
(4)
1
— 1 0,577
—0,562 —0,985 —0,50
(5)
1
— 1
—2,124
2,124
0,562 —0,438 0,24
(6)
1 — 1
1
1 1,547
—3,658
— 1,111
0,42
(7)
1
1
1,534
2,534
—0,15
(8)
1
1
0,856
—0,015
—0,159
—0,06
(9)
1
— 1
1
— 1,939
— 1,939
—0,11
(10)
1
1
1,083
0,015
2,098
0,17
(И)
1 — 1
— 1
1,879
0,289
0,168 0,00
(12)
1
1
1 1
1,894
—3,976 — 1,082
—0,07
(13)
1
—2,097
2,097 —0,289
0,711
0,23
(14)
1
1
0,203
1,203
—0,15
(15) 1
—1 1
0,000
—0,14
(16)
1
1 — 1
— 1
— 1,000
—0,40
(17) 1 1
1
0,000
0,50
(18)
1
1
— 1 1
1,000
0,05
W
Контроль:
0,32—2,10
0,58 0,98—0,93 0,44 2,39
0
Sty = 2ft = SS'j = ZpfVi =
О
| 0 I 0 | 0 I 0 j 0,000| 0,000|
0,0001
[pv
2
] = 1,34
— [kw] = 1,34
0,0001 0,03
Если требуется оценить точность определения не только длины,
но и дирекционного угла той же стороны
а
з4 = а
21
— (7 —5) +
(14
—13) ± 180°,
то весовая функция для него запишется в виде
fa = Да
з4
= (5) — (7) — (13) + (14).
Составление условных уравнений, включая выборку исходных
данных и выписку результатов измерений, выполняют в две руки,
так как допущенные на этой стадии ошибки в вычислениях обна-
ружатся только после уравнивания сети, что приведет к неизбеж-
ности повторных вычислений. При этом должна быть обеспечена
полная независимость в работе обоих вычислителей, сличаются
окончательно составленные ими уравнения.
На каждом этапе вычислений, где есть возможность организа-
ции дополнительного контроля, его непременно надо использовать.
Некоторые из таких контролей указаны выше.
118
