Yanushkevich S.N., Wang P.S.P., Gavrilova M.L., Srihari S.N. (eds.) Image Pattern Recognition. Synthesis and Analysis in Biometrics
Подождите немного. Документ загружается.


April 2, 2007 14:42 World Scientific Review Volume - 9in x 6in Main˙WorldSc˙IPR˙SAB
38 Synthesis and Analysis in Biometrics
(i-1, j-1)
(i, j-1)
(i-1, j)
(i, j)
V
(
--
b
j
)
V
(
a
i
-
)
V
(
a
i
b
j
)
More formally, there are three possibilities:
a
b
,
−
b
,and
a
−
. The figure on the left
depicts the cell (i, j) and possible scores. For
each aligned pair
A
B
,whereA and B are
either normal sequence entries or gaps, there
is an assigned score σ
A
B
. The total score of
a pairwise alignment is defined to be the sum
of the σ values of all aligned pairs.
Objective function. The central problem in sequence matching is to find
a mathematical function, so called objective function, which will be able
to measure the quality of an alignment. Such an objective function should
incorporate everything that is known about the sequences including their
structure, functionality and a priory data. These data are rarely known
and usually being replaced with sequence similarity based on metrics and
scoring.
Metrics and scoring. The main idea of metrics is to get a universal
mechanism of comparing two sequences. Metrics can vary depending on the
objective function, they can embrace distance measures and/or correspond
to statistical computations. The scoring is determined by the amount of
credit an alignment receives for each aligned pair of identical entities (the
match score), the penalty for aligned pairs of non-identical entities (the
mismatch score), and the gap penalty for the alignment with gaps. A
simple alignment score can be computed as follows:
K
k=1
gap penalty; if a
i
=
−
or b
j
=
−
,
match score; if no gaps and a
i
= b
j
,
mismatch score; if no gaps and a
i
= b
j
.
Data alphabet. The alphabet for sequence processing in case of
curvature, velocity and pressure are represented originally by continuous
values and cab be encoded by integers forming a multiple-valued
representation. This encoding procedure can be based on learning rules
and/or discretization principles for continuous sequences
[
13
]
.
Example 2.2. Let us apply the alignment technique described above for
two sequences {1, 2, 1, 4, 2, 1, 4} and {1, 3, 2, 3, 4} assuming that the
gap penalty is −1, the match score is +1, and the mismatch score is 0.
The global alignment of the two sequences is equivalent to a path from the
upper left corner of the matrix to the lower right. A horizontal move in
the matrix represents a gap in the sequence along the left axis. A vertical

April 2, 2007 14:42 World Scientific Review Volume - 9in x 6in Main˙WorldSc˙IPR˙SAB
Signature Analysis, Verification and Synthesis 39
move represents a gap in the sequence along the top axis, and a diagonal
move represents an alignment of nucleotides from each sequence. To fill in
the matrix, we take the maximum value of the three choices (moves).
13234
0 −1 −2 −3 −4 −5
1 −1
3 −2
1 −3
4 −4
2 −5
1 −6
4 −7
13234
0 −1 −2 −3 −4 −5
1 −1 1 0 −1 −2 −3
3 −2 0 2↓ 1 0 −1
1 −3 −1 1↓ 2 1 0
4 −4 −2 0 1 2 2
2 −5 −3 −1 1 1 2
1 −6 −4 −2 0 1 1
4 −7 −5 −3 −1 0 2
Using the global alignment algorithm, we obtain the following alignment:
13 −−234
13 1 4214
. The total score is 2.
Extending the technique presented above, let us outline a new practical
method for aligning multiple-valued and continuous sequences to calculate
the degree of similarity for signatures. The standard algorithms of
Needleman-Wunsch
[
7
]
and of Smith-Waterman
[
17
]
align sequences by
maximizing a score function that favors matching element pairs over
mismatches and gaps. They tend to become sensitive to the choice of
scoring parameters and therefore less reliable with increasing distance
between sequences. Therefore, for aligning multiple-valued and continuous
sequences we selected the scoring mechanism that depends on data only.
New objective function. Since each element of either multiple-valued
or continuous sequence is described by a numerical value, we can use a
limited set of arithmetic operations on them. Intuitively, the objective
function for the alignment process should minimize the differences between
two given sequences. Moreover, there is no distinction between matches and
mismatches in aligning of multiple-valued and continuous sequences, and
gaps can be replaced by values resulted from interpolation or averaging.
New metrics and scoring. The following scoring based on differences
in values is suggested:
min
M(i, j − 1) + ∆
M(i − 1,j− 1) + ∆
M(i − 1,j)+∆
,where∆=|a
i
− b
j
|.
We use the scoring system which helps to minimize the differences between
two arbitrary sequences. Thus, an optimal matching is an alignment with

April 2, 2007 14:42 World Scientific Review Volume - 9in x 6in Main˙WorldSc˙IPR˙SAB
40 Synthesis and Analysis in Biometrics
the lowest score. The score for the optimal matching is then used to find
the alignment which possesses the following properties:
Property 1. The sequences can be shifted left or right, and the alignment
will not be affected.
Property 2. Gaps are allowed to be inserted into the middle, beginning
or end of sequences. The gap is represented by a value from the affected
sequence (multiple-valued case), or the average/interpolated value from the
neighborhood (continuous case).
Alignment of continuous sequences
There are few existing techniques for measuring correlation between
two continuous sequences, like Cram´er-von Mises
[
2
]
,Kuiper
[
6
]
and
Watson
[
19
]
, but none of them gives the sequence of aligned segments as
the result of performed measurements. In the proposed method, both a
correlation score and two aligned sequences are returned.
Example 2.3. Let us consider two continuous sequences {0.3, 0.1, 0.5,
0.7, 0.0} and {0.1, 0.5, 0.5, 0.0, 0.1}. These sequences are placed along
the top and left margins (left panel). Following the dynamic programming
technique and new metrics previously explained, we obtain both the total
score and the alignment (right panel).
0.3 0.1 0.5 0.7 0.0
0.1
0.5
0.5
0.0
0.1
0.3 0.1 0.5 0.7 0.0
0.1 0.2→ 0.2 0.6 1.2 1.3
0.5 0.4 0.6 0.2 0.4 0.9
0.5 0.6 0.8 0.2 0.4 0.9
0.0 0.9 0.7 0.7 0.9 0.4↓
0.1 1.1 0.7 1.1 1.3 0.5
The resulted aligned sequences with gaps and interpolated values are:
0.30.10.50.70.0 −
− 0.10.50.50.00.1
,
0.30.10.50.70.0 0.0
0.1 0.10.50.50.00.1
.
The total alignment score is 0.5.
The method has been evaluated on sample signature data from an image
processing system
[
14
]
. The alignment is done for two continuous sequences
which represent the speed of writing along the trajectory for the same
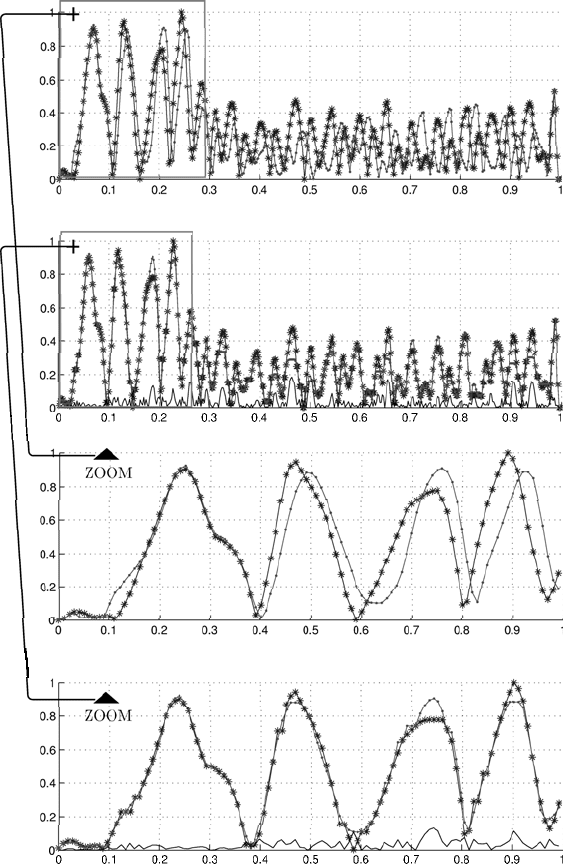
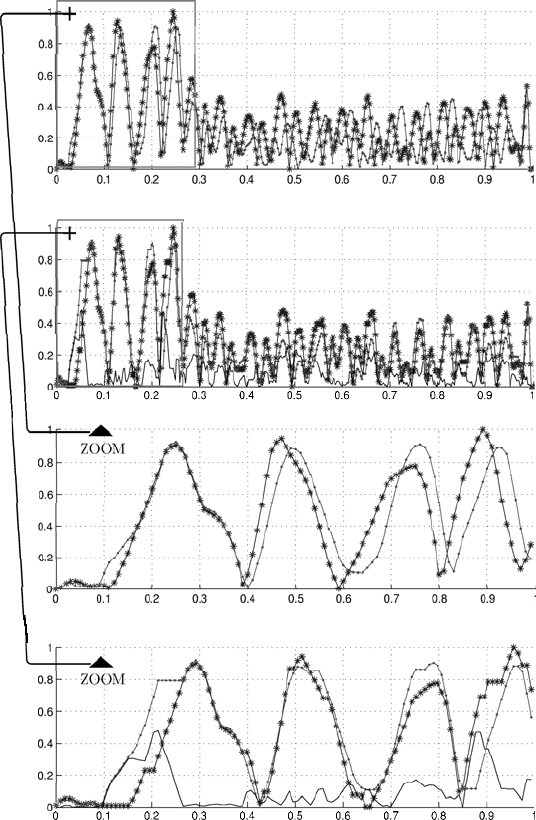
individual. The upper panel of Fig. 2.4 gives the original unaligned
sequences, the panel below shows the output of the alignment.
Exploring various formats of data, the extensions based on cumulative
and difference data processing are outlined below.
April 2, 2007 14:42 World Scientific Review Volume - 9in x 6in Main˙WorldSc˙IPR˙SAB
Signature Analysis, Verification and Synthesis 41
Fig. 2.4. Unaligned and aligned continuous sequences (from top to bottom): unaligned
sequences, aligned sequences, zoomed view of unaligned sequences, and zoomed view of
aligned sequences. The panels show the difference by the solid black line.
April 2, 2007 14:42 World Scientific Review Volume - 9in x 6in Main˙WorldSc˙IPR˙SAB
42 Synthesis and Analysis in Biometrics
Cumulative data. A “rough” alignment can be performed linearly by
using cumulative distributions. Such a “rough” alignment can be used in
two possible scenarios: as a preliminary step to identify regions that will
be further aligned by the dynamic alignment algorithm; and as a real-time
alignment if necessary.
Example 2.4. (Continuation of Example 2.3) Let us consider two
sequences {0.3, 0.1, 0.5, 0.7, 0.0} and {0.1, 0.5, 0.5, 0.0, 0.1},and
cumulative counterparts {0.3, 0.4, 0.9, 1.6, 1.6} and {0.1, 0.6, 1.1, 1.1, 1.2}.
Following the dynamic programming technique and new metrics introduced
previously, we build the alignment matrix and restore the aligned sequences.
0.3 0.4 0.9 1.6 1.6
0.1
0.6
1.1
1.1
1.2
0.3 0.4 0.9 1.6 1.6
0.1 0.2 0.5 1.2 2.4 3.1
0.6 0.4 0.4 0.7 1.7 2.7
1.1 1.2 1.1 0.6 1.1 1.6
1.1 2.0 1.8 0.8 1.1 1.6
1.2 2.9 2.6 1.1 1.2 1.6
The resulted aligned sequences with the total alignment score of 1.6 are:
0.30.40.91.61.6
0.10.61.11.11.2
, but this does not reflect the alignment of original
sequences.
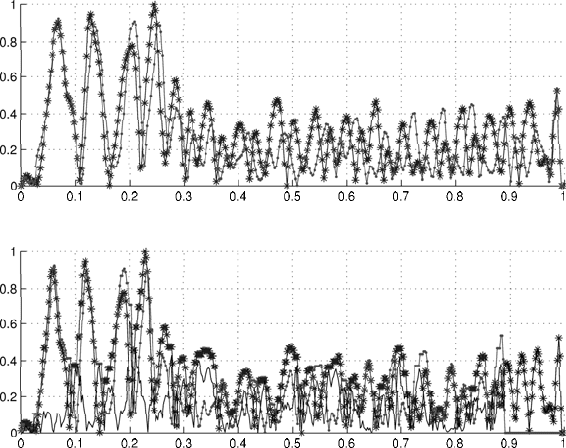
It is illustrated in Fig. 2.5 that the restoration of initial sequences based
on aligned sequences of cumulative data leads to misalignment.
Finite differences. The same method works for the alignment of finite
differences. Thus, aligning the differences gives some clues about the
dynamics of the process, not just statical characteristics. Sequences aligned
by using their finite differences depict where the speed (of changing the
values) is identical. If necessary, the normalization takes place to perform
level adjustments.
Example 2.5. (Continuation of Example 2.3) Let us consider the sequen-
ces {0.3, 0.1, 0.5, 0.7, 0.0} and {0.1, 0.5, 0.5, 0.0, 0.1}, and their difference
counterparts {0.0, −0.2, 0.4, 0.2, −0.7} and {0.0, 0.4, 0.0, −0.5, 0.1}.
0.0 −0.2 0.4 0.2 −0.7
0.0
0.4
0.0
−0.5
0.1
0.0 −0.2 0.4 0.2 −0.7
0.0 0.0→ 0.2 0.6 0.8 1.5
0.4 0.4 0.6 0.2 0.4 1.5
0.0 0.4 0.6 0.6 0.4 1.1
−0.5 0.9 0.7 1.5 1.1 0.6↓
0.1 1.0 1.0 1.0 1.1 1.4
April 2, 2007 14:42 World Scientific Review Volume - 9in x 6in Main˙WorldSc˙IPR˙SAB
Signature Analysis, Verification and Synthesis 43
Fig. 2.5. Unaligned sequences (top) and misaligned sequences restored based on
cumulative data processing (bottom).
The total alignment score is 1.4. The resulted aligned sequences with gaps
and interpolated values are:
0.0 −0.20.40.2 −0.7 −
− 0.00.40.0 −0.50.1
and
0.0 −0.20.40.2 −0.7 −0.7
0.0 0.00.40.0 −0.50.1
.
It reflects the alignment of original sequences.
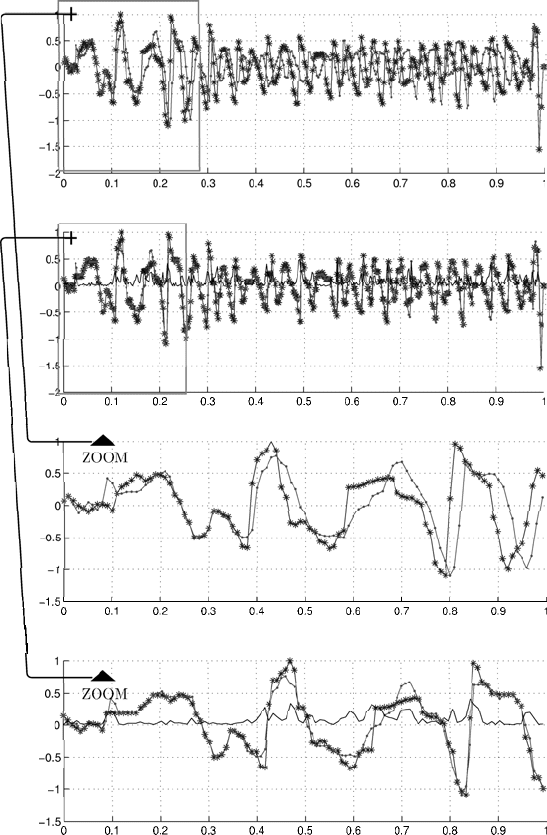
Figure 2.6 depicts two unaligned (upper panel) and aligned (lower panel)
sequences of finite differences. It is shown in Fig. 2.7 that the restoration
of initial sequences based on aligned sequences of difference data gives well
aligned sequences.
2.3.2. Algorithm and Experimental Results
Since the exhaustive search for all possible alignments is an NP-complete
problem, it is impossible to compute in reasonable amount of time
any real sequences. By applying dynamic programming principles, the
computational complexity is in O(n × m). The algorithm works in four
steps:
April 2, 2007 14:42 World Scientific Review Volume - 9in x 6in Main˙WorldSc˙IPR˙SAB
44 Synthesis and Analysis in Biometrics
Fig. 2.6. Unaligned and aligned sequences of finite differences (from top to bottom):
unaligned sequences, aligned sequences, zoomed view of unaligned sequences, and
zoomed view of aligned sequences. The panels show the difference by the solid black
line.
April 2, 2007 14:42 World Scientific Review Volume - 9in x 6in Main˙WorldSc˙IPR˙SAB
Signature Analysis, Verification and Synthesis 45
Fig. 2.7. Unaligned and well aligned sequences based on difference data processing
(from top to bottom): unaligned sequences, aligned sequences, zoomed view of unaligned
sequences, and zoomed view of aligned sequences. The panels show the difference by the
solid black line).
April 2, 2007 14:42 World Scientific Review Volume - 9in x 6in Main˙WorldSc˙IPR˙SAB
46 Synthesis and Analysis in Biometrics
Step 1. The sequences A and B are placed along the left margin and on
the top of the matrix M. There is no need for initialization because
the scoring is based on data only.
Step 2. Other elements of the matrix are obtained by computing the
difference ∆ = |a
i
− b
j
| and finding the maximum value among the
following three values:
M(i, j)=min
M(i, j − 1) + ∆
M(i − 1,j− 1) + ∆
M(i − 1,j)+∆
.
Step 3. The dynamic programming algorithm propagates scores from the
matching start point (upper-left corner) to the destination point (lower-
right corner) of the matrix. The score that ends up in the lower-right
corner is the optimal sequence alignment score. After finding the final
score for the optimal alignment, the final similarity between the two
sequences is computed by considering the final optimal score and the
length of the two sequences.
Step 4. The optimal path is then achieved through back propagating from
the destination point to the starting point. In all given examples, the
optimal path found through back propagating is connected by arrows.
This optimal path tells the best matching pattern.
Multiple-valued and continuous sequences are widely used in the area
of pattern recognition and signature comparison, where the values describe
certain features like curvatures, angles, velocity, etc. and the alignment of
sequences often corresponds to the decision making procedure. Biometrical
applications are good examples of sequence processing. For example,
by aligning and comparing sequences from handwritten signatures, it is
possible to build a reliable and robust verification system (see Fig. 2.8).
Sequence alignment and matching is an important task in multiple-
valued and continuous systems like biometrics in order to group similar
sequences and identify trends in functional behavior. Accurate processing
and sequence comparison depend on good correlation measures between
sequences. This section gave an outline of methods used in sequence
processing and their applications to signature comparison. We introduced
a new similarity measure based on sequence alignment and extended
this approach to various data formats. Having a robust mechanism for
signature analysis and comparison, there is a need in getting enough distinct
signatures for testing and benchmarking. The next section introduces
some methodological principles and techniques for signature modeling and
synthesis.

April 2, 2007 14:42 World Scientific Review Volume - 9in x 6in Main˙WorldSc˙IPR˙SAB
Signature Analysis, Verification and Synthesis 47
Fig. 2.8. Alignment scores for continuous sequences in signature verification. The range
of colors corresponds to the white, showing the minimum similarity score, and gradually
changing to the black, representing the maximum similarity score.
2.4. Signature Synthesis
The modeling and simulation in biometrics, or inverse problems of
biometrics have not been investigated until recently
[
18
]
. However, the
demand for synthetic biometric data is now led to many practical and
important applications. Thus, in signature processing, synthetic signatures
are used to test the system and evaluate the performance of signature
recognition systems.
2.4.1. Signature Synthesis Techniques
This section focuses on the basics of signature synthesis techniques. Known
approaches to analysis and synthesis of signatures can be divided into two
distinct classes:
• Statistical approaches use the fact that a signature shape can be
described by a limited set of features. These features are statistically
characterized.
• Rule-based approaches assume that a signature is the composition of
a limited number of basic topological primitive which can be formally
