Юрков Н.К. Интеллектуальные компьютерные обучающие системы

Подождите немного. Документ загружается.

181

После получения на основании описанной процедуры мно-

жества

описаний учебных материалов предметной области при

заданном



и проверки для каждого описания условия (4.17) дела-

ется вывод о возможности выбора того или иного алгоритма обу-

чения.

4. Если при заданном



не удалось определить приемлемый

алгоритм, исходя из знаний, заложенных в модели предметной об-

ласти, воспользуемся способом определения алгоритма, имеющего

максимальную близость к одному из полученных описаний мно-

жества

по критерию Рао. Этот критерий, однако, обеспечивает

меньшую точность в связи с тем, что фиксирует лишь разницу в

наличии тех или иных свойств, не учитывая их значений.

Те свойства ФО, которые принадлежат

и не принадле-

жат

, в ходе обучения контролируются учителем с помощью

средств формальной оценки свойств.

На основе рассмотренных типовых случаев определения алго-

ритма, приемлемого для обучения данного учебного материала с за-

данным ФО

с учетом качественных характеристик, предлагается

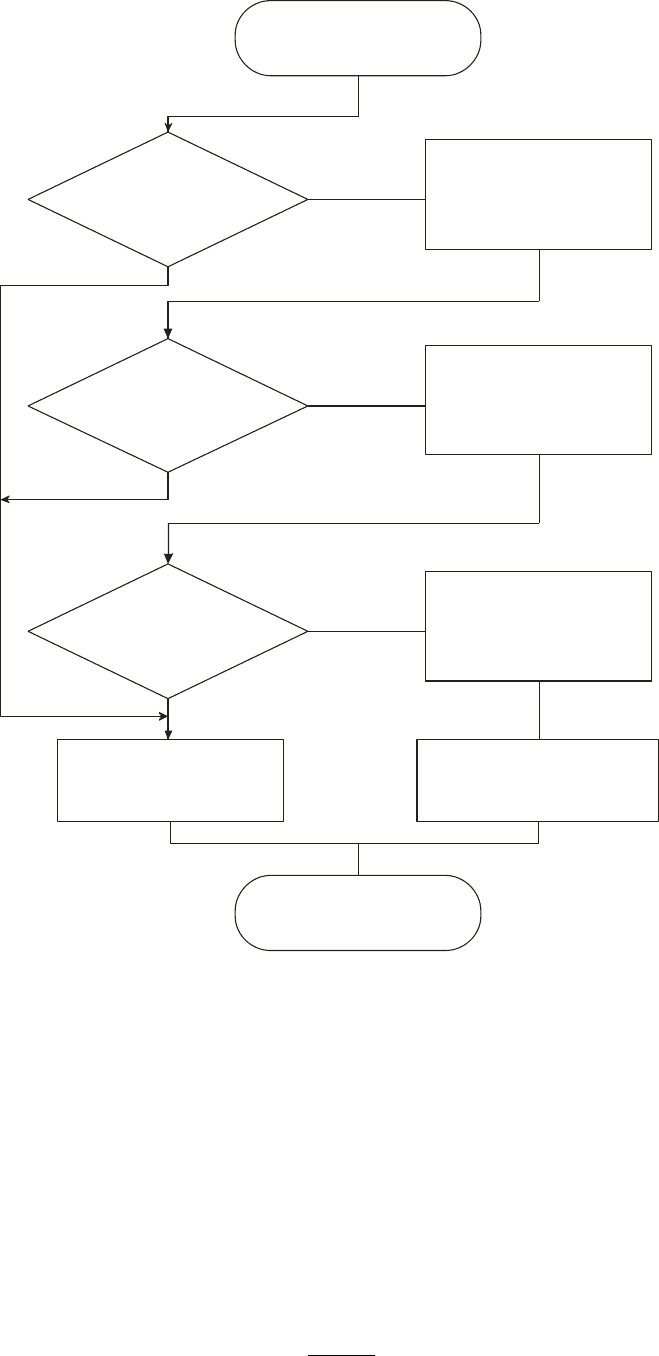
процедура, укрупненная схема которой представлена на рис. 42.

Одним из наиболее распространенных подходов к задаче

учета временных характеристик при оценке альтернативных обу-

чающих процедур является имитационное моделирование. В ре-

зультате сравнительного анализа результатов моделирования дела-

ется вывод о предпочтительности того или иного алгоритма. В то

же время имитационное моделирование имеет ряд недостатков.

Предлагается способ учета временных характеристик обу-

чающих процедур на основе информации, полученной на этапе ис-

следования предметной области обучения.

На основе анализа работы процедуры

получаем зависи-

мость времени ее работы от номера

шага процесса обучения

(шаг – предоставление одного кванта учебной информации, кон-

трольный вопрос, тест и т.д.):

()

t f n

Суммарное время работы

на

шагов есть

()

T f i





182

Начало

Попытка уменьшить

количество свойств

ФО на основе модели

качества процесса

обучения

Существует

процедура,

удовлетворяющая

Попытка уменьшить

количество свойств

ФО на основе

корреляционной модели

свойств

Возможна

оценка описания

по Хэммингу

Оценка описания

по критерию Рао

Формирование множества

процедур, приемлемых

для обучения

Оценка описаний

по критерию

Хэмминга

Конец

Возможна

оценка описания

по Хэммингу

Рис. 42. Процедура формирования множества алгоритмов обучения

с учетом критериев качества

Учитывая, что априорный показатель качества обучающих

алгоритмов есть безразмерная величина, введем в качестве вре-

менного параметра в

относительный показатель, характери-

зующий время выполнения

-й процедуры

по отношению ко

времени работы процедуры, имеющей максимальную продолжи-

тельность

max



183

Применение интегральных временных характеристик

max

позволяет оценить общее время работы процедур и вы-

брать одну из них в начале процесса обучения, однако не дает воз-

можности отразить динамику работы процедур. Для более точной

оценки временных характеристик обучающих процедур в процессе

их работы предлагается использовать вместо

max

времен-

ные зависимости для каждого шага обучения

max

соответст-

венно.

Таким образом, искомый функционал

, позволяющий оце-

нивать приемлемость обучающих процедур с учетом их качест-

венных и временных характеристик, имеет вид

max

BAF



. (4.25)

Предложенный метод выбора алгоритма обучения с учетом

экспертных знаний, предоставленных в моделях предметной облас-

ти, отличается от применяющихся в настоящее время подходов тем,

что адаптирует алгоритмическое и программное обеспечение

ИКОС не к классу учебных материалов, а непосредственно к кон-

кретной теме, разделу предметной области, причем возможность

выбора новой обучающей процедуры существует на каждом шаге

процесса обучения. Эти особенности представляют возможность

гибкой смены обучающих стратегий в зависимости от изменения

ситуации обучения, усталости обучаемого, различных отвлекающих

факторов и т.п.

Таким образом, доказана актуальность данной работы, свя-

занной с достижением компромисса между преимуществами си-

туационного подхода и ограничениями со стороны его практиче-

ской реализуемости на стандартном аппаратном обеспечении за

счет дополнения традиционного набора атрибутов составных час-

тей объекта атрибутами, поддерживающими функционирование

концептуальной модели объекта, и разработки методов анализа и

синтеза программного обеспечения задачи моделирования в рам-

ках полученной формализации. При этом не рассматриваются

вопросы реализации прямых и обратных связей между моделью и

исследуемым объектом, поскольку специфика управления сущест-

венно дифференцирована для различных предметных областей.

184

Предложено совместное хранение фактов и пользовательских

правил в общей концептуальной памяти. Общий список констант,

на основе которого строятся факты и правила концептуальной па-

мяти, объединяет обозначения понятий, их экземпляров и введен-

ных пользователем бинарных отношений. Атомарный элемент хра-

нения в концептуальной памяти – это либо константное значение

отношения (заданного в языке или пользователем), либо предикат

отношения в том или ином правиле пользователя. Правила опера-

ционной семантики отношений в виде образцов, независимых от

конкретного наполнения базы знаний, хранятся в отдельной семан-

тической памяти. Построение конкретных правил на основе образ-

цов и их последующее применение осуществляются в процессе до-

казательства запроса к базе знаний. Возможность применения этих

правил определяется фактами концептуальной памяти. Уровни под-

робности учебного материала введены в модель для того, чтобы

обеспечить несколько вариантов представления обучающей стра-

ницы для обучаемых с различными уровнями подготовки.

На основе функционально-целевого подхода (ФЦП) иерархия

целей используется не только как обычное средство наглядного

структурного описания, но и как инструмент структурно-алгорит-

мического проектирования системы, обеспечивающий учет осо-

бенностей структуры предметной области. Модели, разработанные

с помощью ФЦП, основаны на двухоперационных алгебрах целей

и действий. Функционально-целевой подход вводит соответствие

между целями различных уровней концептуальной модели по

принципу: каждой цели соответствуют функции, обеспечивающие

ее достижение, которые, в свою очередь, являются целями, дости-

гаемыми на следующем, более низком уровне иерархии модели.

Использование этих моделей обеспечивает формальную основу

синтеза систем, в структурно-алгоритмической организации кото-

рых отражена структура целей моделирования. Таким образом,

ИКОС является организованной совокупностью, предназначенной

для решения множества задач, которые образуют классы G

объ-

ектно ориентированных задач (G = {G

}, i = 1, …, N), где N – число

классов. Каждый из представителей классов, в свою очередь, раз-

бивается на совокупность методо-ориентированных процессов.

Разработана методика построения алгоритмов оценивания

параметров, не требующих априорной информации о статистиче-

ских свойствах элементов последовательности. В связи с тем, что

параметры исследуемой системы являются нестационарными, для

185

получения положительных результатов следует применить на-

страиваемую модель.

Предлагается алгоритм оценивания параметров после его на-

стройки на конкретном объекте либо на выборке, полученной на

конкретном объекте впоследствии. Этот алгоритм может давать

оценки приемлемой точности в любой момент S. Решающим дос-

тоинством предполагаемой модификации обычных рекуррентных

алгоритмов идентификации является ненадобность дополнитель-

ных, как и вообще каких бы то ни было предположений, относи-

тельно свойств помех. Благодаря этому алгоритм идентификации

при нестационарных помехах и скорость его сходимости не зави-

сят от их свойств. Подобные алгоритмы могут оказаться полезны-

ми в том случае, когда вероятностные свойства помех изменяются

с ростом S. Кроме этого, они представляются универсальными,

одинаково пригодными в случае как постоянных, так и дрейфую-

щих параметров.

Разработана формальная рекуррентная модель организации

действий (и следовательно, алгоритмов управления обучением)

в многоуровневых ИКОС, которая представляет собой совокуп-

ность элементов множества



, две алгебраические операции





и систему отношений эквивалентности действий по выполне-

нию целевой задачи системы. Таким образом, общая модель ИКОС

основана на формализации процесса обучения как процесса целена-

правленного пополнения аппарата понятий и совершенствования ба-

зы знаний обучаемого. Модель представляет собой граф, множество

вершин которого отождествлено с действиями учителя в процессе

организации и реализации процедуры обучения, а множество ребер

определяет связи между действиями и порядок их выполнения.

Проведен анализ различных способов представления знаний

и на основе его результатов предложена организация смысловой

модели предметной области обучения в виде набора моделей

учебных разделов, тем и т.д., организованных на основе опреде-

ленных семантических отношений и описывающих отдельные

предметные области и связи между ними, которая позволяет обес-

печить соответствие предметной области в ИКОС семантическому

содержанию знаний обучаемого. В целях повышения адаптацион-

ных возможностей ИКОС к различным психофизиологическим ти-

пам обучающихся, к изменяющимся условиям обучения, к поме-

хам во время обучения разработан способ структурной адаптации

программного обеспечения к данной предметной области с учетом

186

качественных и временных характеристик операционных компо-

нентов, базирующийся на использовании информации, хранящейся

в моделях учебных материалов предметной области, и позволяю-

щий осуществлять гибкую смену стратегий обучения с учетом

особенностей конкретного обучаемого.

4.3. Методика количественного анализа соотношения

декларативных и процедурных знаний

в предметной области обучения

Динамичное развитие современной науки влечет за собой

быстрые изменения в сфере профессиональных знаний, умений и

навыков современных специалистов. Поэтому на сегодняшний

день важной задачей является ускорение процесса подготовки и

постоянная поддержка их высокого профессионального уровня.

Одной из эффективных возможностей решения этой задачи

является применение интеллектуальных компьютерных обучаю-

щих систем (ИКОС). Поэтому разработка ИКОС, объединяющих

процессы обучения и тренинга, обладающих эффективной страте-

гией управления обучением, является актуальной задачей.

Решение задачи комплексного применения различных СО с

единой БЗ затруднено сложностью анализа конкретной предмет-

ной области с точки зрения соотношения двух основных аспектов

человеческого знания – декларативного и процедурного. Первый

характеризует существующие факты и закономерности и носит

повествовательный характер, второй связан с описанием способов

и процедур решения задач.

Согласно принятой методологии каждому тематическому

фрагменту УИ в зависимости от соотношения декларативной и

процедурной составляющих соответствует свое место в последова-

тельности вывода учебного материала. Для повышения эффектив-

ности стратегии управления обучением разработана методика ко-

личественного анализа соотношения декларативных и процедур-

ных знаний в предметной области обучения.

В силу того, что какой-либо крупный фрагмент знаний (те-

матический блок УИ) трудно однозначно отнести к множеству

декларативных или процедурных знаний, проведем анализ МПО с

позиций теории нечетких множеств [6365].

Методика распределения УИ по этапам обучения заключается

в переборе всех тематических блоков учебной информации пред-

метной области и присвоении каждому из них степени принадлеж-

187

ности к процедурному виду знания. Затем проводится их распреде-

ление в порядке возрастания степени принадлежности. Таким обра-

зом, в итоге получаем ряд тематических блоков УИ, в котором пер-

выми будут блоки с содержанием теоретических (декларативных)

знаний, а затем все более тяготеющие к практическому (процедур-

ному) знанию.

Тематический блок учебной информации (терминал) состоит

из декларативной и процедурной частей. Декларативная часть со-

держит фреймы «описания». Каждый фрейм «описание» содержит

в себе описание какого-либо факта (закономерности). Сумма

фреймов «описаний» терминала – декларативная емкость термина-

ла (n).

Процедурная часть содержит фреймы «ситуации». Каждый

фрейм «ситуация» содержит в себе пошаговое выполнение какой-

либо процедуры (алгоритма). Сумма шагов всех фреймов «описа-

ний» терминала – декларативная емкость терминала (SP).

Тогда емкость тематического блока учебной информации

(терминала) равна

Т = { SD, SP }.

Относительная процедурная емкость тематического блока

учебной информации (терминала) равна:





Относительная декларативная емкость тематического блока

учебной информации (терминала) равна





Множество значений относительной и процедурной емкостей

тематического блока учебной информации (терминала) находится

в промежутке от 0 до 1. Поэтому при условии SD ≠ 0 и SP ≠ 0,

SD + SP = 1.

Введем лингвистическую переменную с именем «Знание»,

обозначенную как Z, принимающую значения «Декларативное» и

«Процедурное», обозначенные соответственно D и P:

Z = {D, P}.

Значение лингвистической переменной P опишем нечетким

множеством:

P = {x, µP(x) | x  U};

188

где х – значение относительной процедурной емкости тематиче-

ского блока учебной информации (терминала); µP(x) – функция

принадлежности, характеризующая степень принадлежности x

значению лингвистической переменной P; U – множество значе-

ний относительной и процедурной емкостей тематического блока

учебной информации (терминала).

Значение лингвистической переменной D опишем нечетким

множеством:

P = {y, µD(y) | y  U},

где y – значение относительной процедурной емкости тематиче-

ского блока учебной информации (терминала); µD(y) – функция

принадлежности, характеризующая степень принадлежности y

значению лингвистической переменной D;

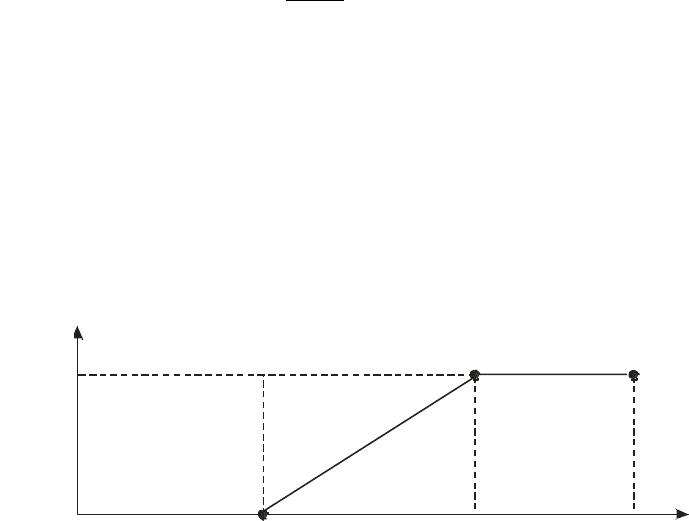
В качестве функции принадлежности, характеризующей сте-

пень принадлежности x значению лингвистической переменной P,

выбрана функция S симметричного вида (рис. 43), описываемая

формулой



















ñëó÷àÿõ.îñòàëüíûõâ0

)( cxb

bxa

Лингвистическая переменная «Знание» принимает значение

«Процедурное» на отрезке от 0 до 0,3 и «Декларативное»  на от-

резке от 0,7 до 1.

0,3

0,5

0,7

Декларативное

Процедурное

Рис. 43. Вид функции S симметричного вида

На основе проведенного количественного анализа соотноше-

ния декларативных и процедурных знаний в предметной области

обучения получена табл. 6.



(х)

189

Таблица 6

Соответствие степени принадлежности учебной информации

этапам обучения

Название этапа

Средства обучения

Коммуникативная

стратегия

1. Начальный

Мультимедиа

средства

под управлением

ИКОС

Информирующая +

+ оценочная

«Декла-

ративное»

2. Ключевой

3. Материальный

Функциональные

тренажеры

под управлением

ИКОС

Продуктивная +

+ оценочная

(информирующая +

+ оценочная)



4. Речевой

Процедурные

тренажеры

под управлением

ИКОС

Продуктивная +

+ оценочная

«Про-

цедурное»

5. Умственный

Таким образом, разработанная методика количественного

анализа соотношения декларативных и процедурных знаний в

предметной области обучения на основе теории нечетких мно-

жеств позволяет автоматизировать распределение тематических

блоков учебной информации по этапам обучения.

4.4. Интерфейс технических систем

Развитие информационных технологий создало необходи-

мую основу для перехода компьютерных средств обучения из ин-

формационного приложения в новое средство обучения, радикаль-

но изменяющее технологию подготовки современных специали-

стов, развивая у них способность к исследованию, решению не-

стандартных задач, работе с реальными приборами и лаборатор-

ным оборудованием. Для этого обучаемого необходимо вовлечь в

специально организованный учебный научно-познавательный

процесс, который выступает в роли реального процесса научного

познания, что требует от систем обучения управления различными

видами средствами обучения.

В качестве внешнего объекта исследования могут выступать

БЗ, САПР или АЛК, а значит, задача совместимости является од-

ной из наиболее актуальных. Поэтому за основу ИТС систем

ИКОС следует взять модель взаимодействия открытых систем

(Open System Interconnection, OSI). Изначально модель OSI была

190

разработана для стандартизации взаимодействия компьютеров и

другого сетевого оборудования в вычислительных сетях, она заме-

чательно подходит для описания взаимодействия ИКОС с внеш-

ним объектом исследования.

Организация взаимодействия между двумя устройствами яв-

ляется сложной задачей. Как известно, для решения сложных задач

используется универсальный прием – декомпозиция, т.е. разбиение

одной задачи на несколько задач-модулей. Декомпозиция состоит

в четком определении функций каждого модуля, а также порядка

их взаимодействия (интерфейсов). В результате достигается логи-

ческое упрощение задачи, а кроме того, появляется возможность

модификации отдельных модулей без изменения остальной части

системы.

При декомпозиции часто используют многоуровневый под-

ход. Он заключается в следующем:

 все множество модулей, решающих частные задачи, раз-

бивают на группы и упорядочивают по уровням, образующим ие-

рархию;

 в соответствии с принципом иерархии для каждого проме-

жуточного уровня можно указать непосредственно примыкающие к

нему соседние вышележащий и нижележащий уровни (рис. 44);

 группа модулей, составляющих каждый уровень, должна

быть сформирована таким образом, чтобы все модули этой группы

для выполнения своих задач обращались с запросами только к мо-

дулям соседнего нижележащего уровня;

 результаты работы всех модулей, отнесенных к некоторо-

му уровню, могут быть переданы только модулям соседнего вы-

шележащего уровня.

Такая иерархическая декомпозиция задачи предполагает чет-

кое определение функции каждого уровня и интерфейсов между

уровнями. Интерфейс определяет набор функций, которые ниже-

лежащий уровень предоставляет вышележащему. В результате ие-

рархической декомпозиции достигается относительная независи-

мость уровней, а значит, возможность их автономной разработки и

модификации.

Средства решения задачи организации взаимодействия меж-

ду устройствами представлены в виде иерархически организован-

ного множества модулей. Например, модулям нижнего уровня

можно поручить вопросы, связанные с надежной передачей ин-