Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань

Подождите немного. Документ загружается.

Елементи математичної статистики І КІ

4. Будуємо довірчий інтервал, використовуючи рівність (3.41)

або

Остаточно отримаємо

nSl

nS«

—

< -

2 л 2

ХГ Х\

20-10

< оі <

33,7 * 8,6

5,935 < сг

< 23,256 .

Якщо потрібно побудувати довірчий інтервал для середнього квадратичної о

відхилення, то використовуємо рівність (3.42) і остаточно одержимо

2,34 <а

< 4,82.

§ 3.6. Статистична перевірка гіпотез

3.6.1. Загальна задача перевірки гіпотез

Одним із найважливіших розділів математичної статистики є статистична

перевірка гіпотез. При цьому під гіпотезою розуміють певні припущення про вигляд

невідомого розподілу або про невідомі параметри деяких відомих розподілів

досліджуваної величини. Такі гіпотези називають статистичним». До

проблеми висування статистичної гіпотези приводять такі, досить часто

виникаючі задачі, як порівняльна оцінка різних методів спостережені,

(вимірювань) за їх точністю, економічністю, досконалістю методики, а також

порівняння особливостей конструкції геодезичних інструментів та приладів.

Питання про те, за якою ознакою і в яких відношеннях доцільні такі

порівняння, цілком відносяться до компетенції тих спеціальних областей геодезії,

фотограмметрії, гравіметрії, картографії, астрономії, в яких виникають ці задачі.

Однак, при наявності явища розсіювання ознак, за якими необхідно викопані

порівняльну оцінку (наприклад, точність вимірювань або якість інструментів),

обгрунтований висновок можна отримати лише шляхом науково проведеного

аналізу статистичної інформації.

Статистичні дані при цьому розглядаються як деякі вибірки з генеральних

сукупностей, які інформують про поведінку випадкових величин, що цікавлять

дослідника і дозволяють зробити певні висновки про закони розподілу цих

Розділ III

іин. У більшості випадків можна не сумніватися в тому, що величини, які

інюють, мають однаковий закон розподілу ( нормальний, біномінальний

і), але своєрідність закону розподілу кожної із цих величин полягає, як

яло, в різниці значень параметрів: математичного сподівання, дисперсії і т.д.

і, при зміні параметрів і знаходять відображення відмінності в якості методу

рювань, інструментів тощо, які виявляються шляхом співставлення

істичних даних.

[аведемо приклади такого аналізу статистичних даних,

[ехай порівнюються дві серії вимірювань однієї і тієї ж величини двома різними

зювальними приладами. Співставляючи емпіричні дисперсії в цих серіях, можна

)

оцінити, наскільки точність одного з приладів відрізняється від точності іншого,

ібо нехай порівнюються дві чи багато серій вимірювань однієї і тієї ж

чини, які виконані приладами однакової точності але різними методами в

кових фізичних умовах. Науково обгрунтовані висновки про переваги одного

іду над іншими можна отримати співставленням середніх арифметичних

пьтатів спостережень та емпіричних дисперсій.

)тже, перевірка гіпотез полягає в порівнянні статистичних характеристик,

оцінками параметрів законів розподілу. Інакше кажучи, з припущень про

ни розподілу або їх параметри (зі "статистичних гіпотез") приходять до певних

іідків і розглядають наскільки вони виправдовують себе на практиці. Ці

іідки мають характер ймовірнісних міркувань про поведінку деяких

истичних характеристик при зроблених припущеннях.

Іеревірка полягає в обчисленні значень цих характеристик (статистик) за

іми спостережень і в порівнянні їх з тим, що було отримано на основі зроблених

пущень. Такі статистики називаються критеріями перевірки

гистичних гіпотез. Вони є випадковими величинами, значення яких

іачаються з вибірки.

Цля критеріїв перевірки вибирають так звані рівні значущості, які, як правило,

зажаються в %-ах (наприклад q = 5%, 2%, 1% і т. п.) і відповідають подіям, які

них умовах досліджень вважаються практично неможливими (правда, з деяким

иком). Рівні значущості визначають критичну область даного

терія, ймовірність «потрапляння в яку у випадку, коли сформульована гіпотеза

зною, точно дорівнює рівневі значущості, тобто а = ^/100.

Значення критеріїв, які потрапляють ззовні критичної області, утворюють

аткову до неї область "допустимих значень", ймовірність потрапляння до якої

терію при справедливості висунутої гіпотези дорівнюватиме 1 - q / 100. Ця

,ія вважається практично достовірною при тих самих умовах.

Отже, якщо значення нашого критерію, яке обчислено за даними спостережень,

рапляє в критичну область, то висунута гіпотеза відхиляється (спростовується).

Елементи математичної статистики І КІ

Поряд з гіпотезою, яка висувається, завжди формулюють другу гіпотезу, яка

суперечить першій. Першу (основну) називають нульовою гіпотез» і» і

позначають її Н

, а другу - конкуруючою (альтернативною) і позначають //,

Наприклад, якщо нульова гіпотеза полягає в тому, що математичне споді

паї пін

нормального розподілу дорівнює 2,0, то конкуруюча гіпотеза може стверджу

на і

(припускати) що а

2,0. Це позначають так:

а = 2,0; Ну аФ 2,0.

Таким чином, якщо гіпотеза H

відхиляється, то приймається альтерна

інша

гіпотеза Н

Якщо значення критерію опиняється в області допустимих

значень, тоді неможливо стверджувати, що гіпотеза Іі

є справедливою

Можна тільки говорити, що спостережуване значення критерію не суперечнії,

висунутій гіпотезі Н, тобто її можна вважати справедливою доти, доки більше

поширені дослідження (наприклад, при більших обсягах вибірок або з допомогою

іншого критерію) не приведуть до протилежного висновку.

Чим менший рівень значущості, тим менша ймовірність не прийняти гіпотезу,

яка перевіряється, коли вона є вірною, або, як говорять, "зробити помилку

першого роду". Але зі зменшенням рівня значущості через те, що зменшується

чутливість критерію, розширюється область його допустимих значень і

збільшується ймовірність зробити так звану "помилку другого роду", тобі о

прийняти гіпотезу, яка перевіряється, коли вона є невірною, тобто вірною і

альтернативна гіпотеза, яка може бути тільки наближеною до першої

забезпечує

більшу ймовірність потрапляння критерія в область допустимих значень.

Отже, рівень значущості критерія перевірки гіпотези контролює лише помилки

першого роду, але зовсім не визначає степінь ризику, який пов'язаний із

прийняттям невірної гіпотези (тобто можливістю зробити помилку другого роду).

Нехай а - ймовірність помилки першого роду, а /3

—

ймовірність помилки

другого роду. Тоді можна сказати, що для великої кількості вибірок частка хибних

висновків дорівнює а, якщо справедлива гіпотеза H

, та дорівнює Д якщо

справедлива гіпотеза Я, (альтернативна). Помилки першого і другого роду можна

подати у вигляді такої таблиці:

Таблиця 3.4

справедлива

хибна

відхиляється Помилка першого роду

із ймовірністю

СС

Справедливе рішення

із ймовірністю 1-/3

приймається

Справедливе рішення

із ймовірністю 1-а

Помилка другого роду

із ймовірністю /3

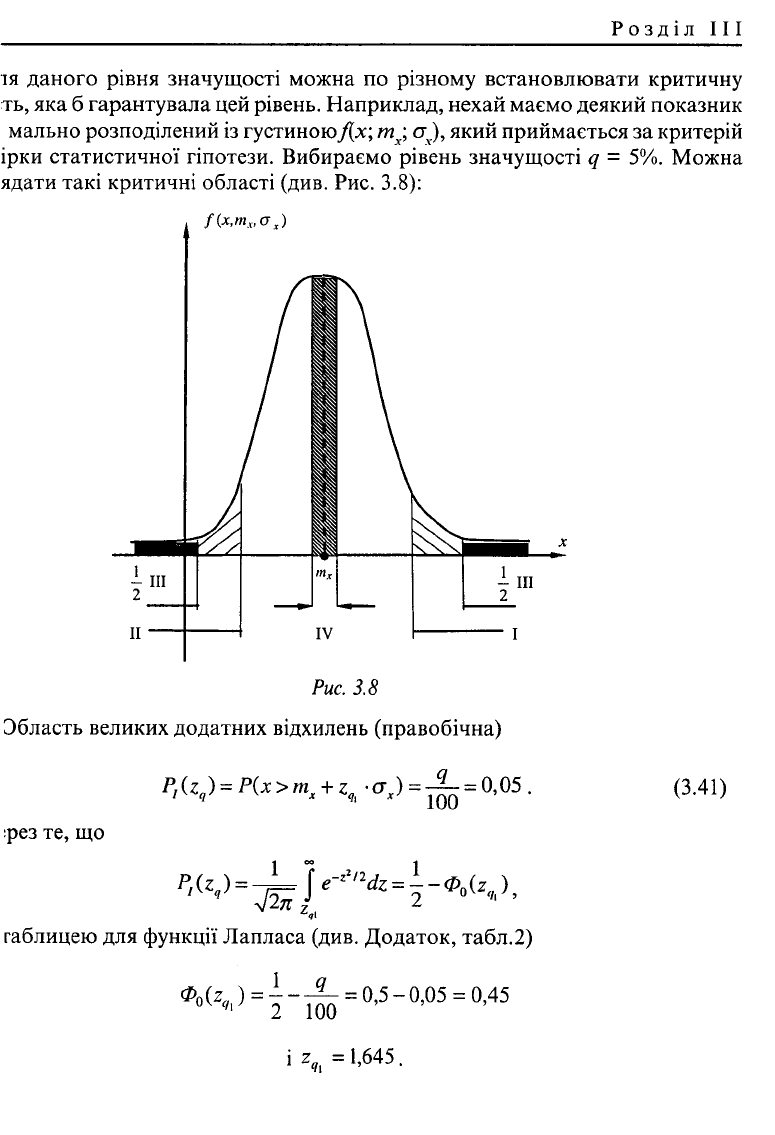
Розділ III

ія даного рівня значущості можна по різному встановлювати критичну

ть, яка б гарантувала цей рівень. Наприклад, нехай маємо деякий показник

змально розподілений із густиноюДх; т

; а.), який приймається за критерій

ірки статистичної гіпотези. Вибираємо рівень значущості q = 5%. Можна

ядати такі критичні області (див. Рис. 3.8):

Область великих додатних відхилень (правобічна)

Р,tz

) = Р(Х >т

х +

.<j

) = JL = 0,05. (3.41)

:рЄЗ ТЄ, ЩО

•'«І

таблицею для функції Лапласа (див. Додаток, табл.2)

, =1,645.

Елементи математичної статистики

І КІ

Зауваження. Тут

далі z - критична точка, яка визначає межу критичної облає

і і

II. Область великих від'ємних відхилень (лівобічна).

р„ (z,) = Р(х <т

- z

) = ^ = 0,05 . (.U2)

Із вище наведених міркувань z = 1,645.

III. Область великих за абсолютною величиною відхилень (двобічна).

P,n(z

) = Р(\Х-т

Чш

•

) = ^ = 0,05. (3.4.1)

У цьому випадку

Р (7

yj2

'Чш

За таблицею для функції Лапласа (див. Додаток, табл.2) із використанням

співвідношення 2Ф

(г

Цш

) = \--~ = 1-0,05 = 0,95 знаходимо Ф

(г

(/ш

) = 0,475,

звідки z = 1,96.

IV. Область малих за абсолютною величиною відхилень (двобічна).

P,v(z

)

= P(\X -m

\<z

4iv

-а

) = ^ = 0,05 . (3.44)

P„(z,) = 2Ф

о(гї(у

) = ^ = 0,05.

100

Така ймовірність дорівнюватиме

Ч_

100

За таблицею (див. Додаток, табл.2) та значенням Ф

(г

^ ) = 0,025, отримаємо

z =0,063.

ЧіУ

Задача найкращого вибору критичної області найчастіше розв'язується так,

щоб критерій перевірки гіпотези мав найбільшу чутливість, тобто щоб

забезпечити найбільшу ймовірність потрапляння критерію перевірки у кри тичну

область, коли справедливою є конкуруюча гіпотеза Я, до основної ІІ

. 11,я

ймовірність називається потужністю критерію. Чим більша потужність

критерію, тим менша ймовірність

зробити помилку другого роду.

Таким чином, потужність критерію - це ймовірність потрапляння самого

критерію (певної статистики) у критичну область при умові, що справедливою є

альтернативна гіпотеза, інакше кажучи, нульова гіпотеза, Я

буде спростована,

якщо вірною є гіпотеза Н

Із наведених міркувань ясно, що завжди існує великий вибір критичної облас ті.

Але з точки зору здорового глузду критичну область треба будувати такою, щоб

Розділ III

кність критерію була б максимальною (дійсно, тоді зменшується ймовірність

бити помилку другого роду). Таким чином, потужність критерію контролює

лки другого роду.

леншити обидві ймовірності а та

одноразово неможливо: якщо зменшувати а,

.втоматично збільшується.

ідповідь на питання "як краще?" залежить від "важкості наслідків" помилок

:ого і другого роду в кожній конкретній задачі. Наприклад, якщо помилка

юго роду викликає більші втрати, а другого роду - менші. Тоді треба

няти якомога менше а. Існує теорема Неймана-Пірсона, за якою можна

вати критичну область для найменшої ймовірності /3 для вже обраної

ірності «(тобто отримати максимальну потужність критерію). На практиці

задача в основному розв'язується інтуїтивно.

лід зауважити, що спростовують гіпотезу більш категорично, ніж приймають,

свіду відомо, що достатньо навести один приклад, який суперечить деякому

іьному твердженню, і воно спростовується. Потрапляння обчисленого

ерію у критичну область є фактом, який можна сприймати як такий приклад,

уперечить гіпотезі Н

і дозволяє її відхилити.

озглянемо тепер конкретні статистичні гіпотези, які перевіряють при

'язуванні різних виробничих (геодезичних в тому числі) задач.

3.6.2. Перевірка гіпотези про рівність центрів розподілу двох нормально

розподілених генеральних сукупностей

Іеревірка такої гіпотези виникає у тих випадках, коли середній результат

:ї серії експериментів суттєво відрізняється від середнього другої серії.

даних

аціях завжди виникає питання: чи можна пояснити розбіжності випадковими

ібками експерименту, або ці розбіжності викликані деякими незауваженими,

давіть невідомими, факторами.

' промисловості така задача виникає при вибірковому контролі якості

•бів, виготовлених на різних установках або при різних технологічних схемах.

геодезичній практиці, користуючись методом порівняння двох середніх

лальних генеральних сукупностей, можна провести точний теоретично-

іірнісний аналіз результатів вимірювань, які отримано однаковими або різними

>ументами, кількома спостерігачами в однакових або різних умовах спостережень,

'озглянемо приклад.

іехай потрібно визначити, чи буде новий спосіб виробництва електроламп

ювати їх тривалість.

іідомо, що середня тривалість їх роботи при існуючому методі виробництва

дає 500 годин.

Елементи математичної статистики І'Л

І КІ

Досліджуючи нову технологію виготовлення електроламп, для деякої

невеликої партії отримали середню тривалість роботи 560 годин.

У статистичному сенсі виникає задача порівняння двох генералі.них

сукупностей з різними центрами розподілу.

Позначимо їх V, (при старому методі) і v

(при новому). При цьому ми не

знаємо точного значення v

, але наближено його можна оцінити за вибірковії ми

даними.

Висуваємо нульову гіпотезу i/

: v, = v

= vi альтернативну H^

Vj Ф

Нехай середнє квадратичне відхилення a- =<7

/vn знайдено та дорівнює 4'•>

годинам (тут х - оцінка центра розподілу другої генеральної сукупності).

За критерій перевірки гіпотези H

в даному випадку природно вибра

нормоване відхилення

Це відхилення має нормальний закон розподілу з параметрами

т_

= 0; а І

Оскільки альтернативною гіпотезою є гіпотеза Я,: v, Ф v

, то за критичну

область краще взяти двобічну область типу III (великих за абсолютною величиною

відхилень)

де z - q%-на межа відхилень, яка задовольняє умову

' '"' 100

і знаходиться з таблиці для функції Лапласа (див. Додаток, табл.2).

Вибираємо рівень значущості q = 5%, тоді критична область визначає ться зі

співвідношення

P{\x-v

\>z

.<T-) = l--jL= f e~^dz = \-20Az

) =

—— = 0,95

'•чт

За значенням ймовірності І

—

/^qq = 0,95 із таблиці (див. Додаток, табл.2)

знаходимо z =1,96. Тепер критична область задаватиметься нерівністю

х -

5001

> 1,96 -45 = 88 (годин).

Отримане із вибірки середнє значення годин знаходиться за межами критичної

області (60 < 88). Це означає, що гіпотеза Н

приймається і відхилення в 60 годнії

може виникати лише під дією випадкових факторів, які супроводжують вибірку.

> Розділ

іакше кажучи, спостереження критерія не досягло "значущих" (суттєвих)

ірів, і в нас ще немає достатньо підстав вважати, що новий спосіб виробництва

гроламп суттєво відрізняється від старого. Потрібні нові випробовування, і

результат буде аналогічний, то треба шукати інший спосіб підвищення

зтривалості електроламп і не приймати до уваги запропонований,

к бачимо, результат перевірки гіпотези залежить від рівня значущості. 5%-

івень означає, що подія (потрапити випадковій величині (x-v

)/a

ичну область) стає неможливою, маючи ймовірність = 0,05. Якщо

шувати цю ймовірність, тоді будемо звужувати довірчі межі та розширювати

ичну область, а тим самим при інших рівних умовах гіпотеза буде частіше

шятися. Такі спростування можуть стати ненадійними, тобто можуть бути

:сені і до вірної гіпотези, через те, що ймовірності порядку 0,2 0,3 вже не

вважати ймовірностями практично неможливих подій,

[ри зменшенні рівня значущості межі розширюються, а критична область

ується, і гіпотеза в такому разі все менше буде спростовуватись навіть у тих

їдках, коли вона вже не буде справедливою. Тобто критерій стане

утливим".

аким чином, треба правильно вибирати критичну область, яка контролює

жність критерія та рівень значущості, хоча, як ми вже відзначали, це

мається інтуїтивно.

[рипустимо тепер, що при повторному випробовуванні електроламп середня

алість їх роботи стала рівною 605 годинам. Тепер при гіпотезі Я

: v, = v

= v

;рнативною буде Я,: v

> v

При такій альтернативі потужність критерія

*-v

)/cr- буде найбільшою у випадку критичної області І типу (великі

тні відхилення),

а співвідношенням (3.41)

P(x>v.+z

•

од =0,05

1 У І л

Злиці інтегралу ймовірностей знайдемо

= 165.

'ритична область тепер визначатиметься так:

х-500 >1,65-45 = 74 {години).

ідхилення годин вже є значущим (74<105). Тому гіпотеза Я

відхиляється

)стовується).

ітже, такий метод виробництва електроламп вже може збільшувати їх

^тривалість.

Елементи математичної статистики

І'Л

Із наведеного прикладу видно певний порядок дій при перевірці статне

ичікн

гіпотези про рівність центрів розподілу різних генеральних сукупностей.

Наведемо його.

1. Формулювання нульової Я

та конкуруючої Я, гіпотез.

2. Вибір та обчислення статистичного (вибіркового) критерія перевірки

гіпотези (К або К, ).

стат. ооч/

3. Вибір рівня значущості (q %).

4. Визначення критичної області та області прийняття гіпотези.

5. Порівняння обчисленого критерія із критичним значенням та іірніінмі їм

статистичного рішення.

Такий порядок зберігається і для перевірки інших статистичних гіпотез.

Розглянемо тепер задачу перевірки гіпотези про рівність центрів рознодшу

різних генеральних сукупностей в загальному випадку.

Нехай досліджуються дві нормально розподілені випадкові величини .V

а )

Маємо дві незалежні вибірки з обсягами n

та п

із генеральних сукупності

величин X та У. Необхідно перевірити гіпотезу Я

: М[Х\ = M[Y\. При ньому

дисперсії генеральних сукупностей а\ та aj можуть бути відомими, лі>о

невідомими.

Розглянемо випадок з відомими дисперсіями а\ та а

Якщо дисперсійні величини X і Y відомі, то для перевірки гіпотези

11'

можна

скористатися тим, що різниця (у - х) двох вибіркових середніх матиме нормалі.ніш

закон розподілу з параметрами М[у -х] = М[у]~М[х] і сг-_-

п,

Якщо гіпотеза Н

є справедливою, то М[у -х] = М[у\ -М[х] = 0 .

За критерій перевірки доцільно брати нормоване відхилення

х- у

z= І

, (3.45)

"і "2

яке буде мати також нормальний закон розподілу з параметрами M[Z] = 0, D[Z\ - I.

Критична область будується в залежності від вигляду конкуруючої гіпотези II

Тут виникають три випадки.

Перший випадок.

Нульова гіпотеза

М{Х) = M(Y), а альтернатива Я,: М{Х) ФМ{Т). У такому

випадку будують двобічну критичну область, таку, щоб ймовірність потрапляння

в неї дорівнювала прийнятому рівневі значущості (якщо II

> Розділ

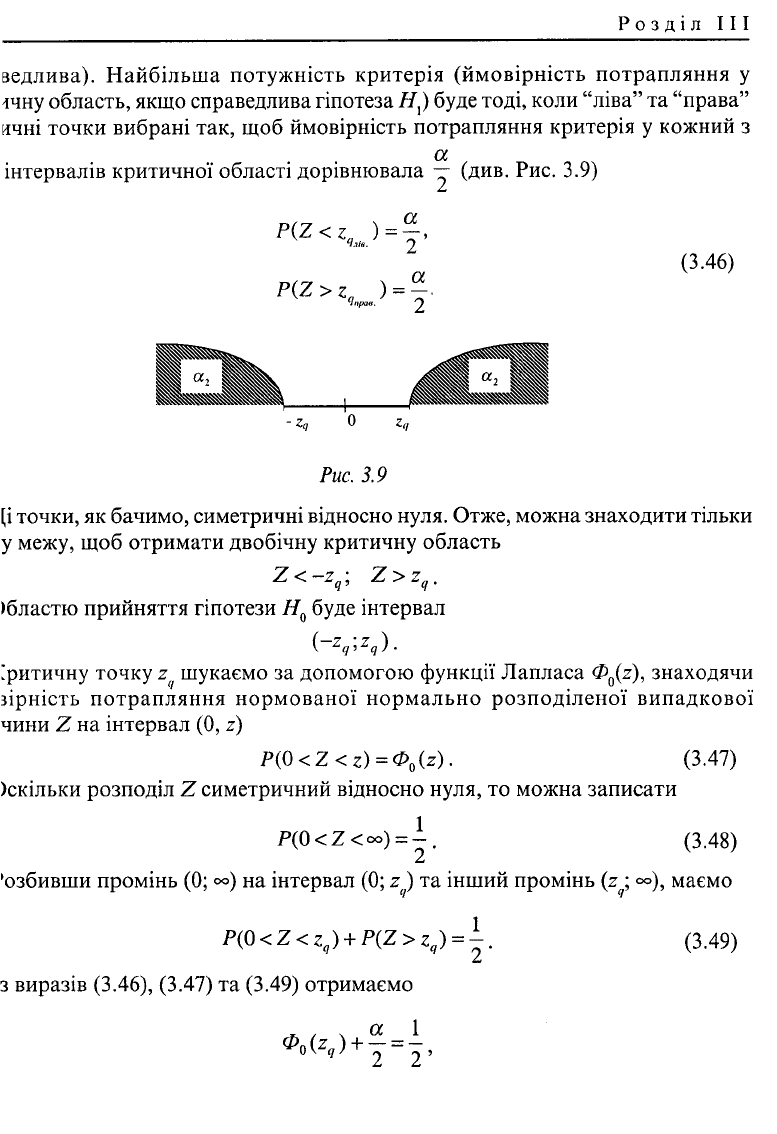
ведлива). Найбільша потужність критерія (ймовірність потрапляння у

ічну область, якщо справедлива гіпотеза #,) буде тоді, коли "ліва" та "права"

ячні точки вибрані так, щоб ймовірність потрапляння критерія у кожний з

інтервалів критичної області дорівнювала — (див. Рис. 3.9)

P(Z<z

J = ~,

P{Z> z ) =

Чправ. "j

(3.46)

Рис. 3.9

(і точки, як бачимо, симетричні відносно нуля. Отже, можна знаходити тільки

у межу, щоб отримати двобічну критичну область

Z<-z

; Z>z

ібластю прийняття гіпотези H

буде інтервал

[ритичну точку z шукаємо за допомогою функції Лапласа Ф

(г), знаходячи

зірність потрапляння нормованої нормально розподіленої випадкової

чини Z на інтервал (0, z)

P(0<Z<z) = Ф

(z). (3.47)

)скільки розподіл Z симетричний відносно нуля, то можна записати

P(0<Z<oo) = I.

(3 48)

'озбивши промінь (0; на інтервал (0; z ) та інший промінь (z ; «>), маємо

Р(0<Z<z

) + P(Z > z

) =

—

з виразів (3.46), (3.47) та (3.49) отримаємо

^ /• ч

а 1

(3.49)