Зенкевич Н.А. Практикум по исследованию операций
Подождите немного. Документ загружается.


4.1. СХЕМА МЕТОДА ВЕТВЕЙ И ГРАНИЦ 91
• Вычисление решений. С любым граничным множеством необходим о однозначно
связать одно допустимое решение задачи. Пусть G
i
граничное множество, тогда су-
ществует единственное допустимое решение x ∈ G
i
. При реализации метода ветвей
и границ необходимо указать, каким образом вычисляется x, если соответствующая
вершина является граничной, при этом ε(G
i
) = φ(x).
• Пересчет оценок.
Если G
1
⊂ G
2
, то min
G
1
φ(x) ≥ min
G
2
φ(x). Поэтому должно выполняться неравенство
ε(G
1
) ≥ ε(G
2
). Таким образом оценки множеств не убывают по включению. При
реализации метода ветвей и границ необходимо разработать процедуру пересчета
оценок в процессе ветвления.
• Критерий оптимальности. Пусть G
1
, . . . , G
r
– множества, которые не подверга-
лись ветвлению. Пусть ε(G
j
) ≤ ε(G
i
), i ∈ [1, r]. Если G
j
– граничное множество, т.е.
ε(G
j
) = φ(x), – то x оптимальное решение задачи дискретного программирования.
• Точность приближенного решения. Пусть G
1
, . . . , G
r
– множества, которые не
подвергались ветвлению. Пусть G
j
– граничное множество и оно находится среди
G
1
, . . . , G
r
. Пусть φ(x) = ε(G
j
), и выполняется неравенство
ε ≤ min
x
φ(x) ≤ φ(x), ε = min
i=
1,r
ε(G
i
).
Тогда число ∆ = φ(x) − ε точность приближенного решения x.
4.1.1 Алгоритм метода ветвей и границ в задаче линейного це-
лочисленного программирования
Рассмотрим задачу линейного целочисленного программирования (ЗЦЛП):
min f(x) = min(
n
X
j=1
c
j
x
j
) (4.1.1)
n
X
j=1
a
ij
= b
i
, i =
1, m; (4.1.2)
x
j
≥ 0, j =
1, n; (4.1.3)
x
j
− целые, j =
1, n; (4.1.4)
92 Глава 4. ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ
ИТЕРАЦИЯ 1. Пусть G
(0)
= G – множество допустимых решений задачи, т.е. выпол-
няются условия (4.1.2)-(4.1.4).
Решая задачу линейного программирования (4.1.1)-(4.1.3) на множестве G
(0)
, полу-
чаем x
0
– оптимальное решение. Если x
0
– целочисленное (все компоненты вектора
x – целые), то x
0
- оптимальное решение задачи линейного целочисленного программи-
рования (4.1.1)-(4.1.4) и вычисления останавливаются.
Если нет, вычисляем оценку ε(G
(0)
) :
ε(G
(0)
) = [(f(x
0
)].
ИТЕРАЦИЯ 2. На входе итерации 2. имеем G
(0)
и x
0
. Пусть x
i0
– нецелочисленная
компонента x
0
.
Ветвление. Строим множества
G
(1)
1
= {x|x ∈ G
(0)
, x
i
≤ [x
i0
]}; (4.1.5)
G
(1)
2
= {x|x ∈ G
(0)
, x
i
≥ [x
i0
] + 1}. (4.1.6)
Решая задачу линейного программирования (4.1.1)-(4.1.3) на множествах G
(1)
1
, G
(1)
2
,
получаем соответствующие оптимальные решения x
1
1
, x
1
2
. Если x
1
i
– целочисленно, то
множество G
(1)
i
– является граничной вершиной дерева ветвления.
Полагаем: ε
1
= ε(G
(1)
1
) = [(f(x
1
1
)], ε
2
= ε(G
(1)
2
) = [(f(x
1
2
)].
Если x
1
i
целочисленное и ε(G
(1)
i
) = min{ε
1
, ε
2
}, то x
1
i
– оптимальное решение ЗЛЦП.
.....
ИТЕРАЦИЯ (k + 1). На входе итерации имеются еще не подвергавшиеся ветвлению
множества G
(k)
1
, . . . , G
(k)
r
. Какие-то из них граничны, какие-то нет. Любое множество
имеет нижнюю оценку и оптимальное решение задачи ЛП (4.1.1)-(4.1.3) на нем. Пусть
x
k
1
, . . . , x
k
r
– решения соответствующих задач ЛП. Некоторые из них целочисленны и
тогда соответствующее множество граничное. Остальные решения нецелочисленны, по-
этому соответствующие множества могут быть подвергнуты ветвлению.
Находим такое множество G
(k)
i
, что выполняется:
ε(G
(k)
i
) = min
j
{ε(G
(k)
j
)}.
В этом случае множество ε(G
(k)
i
) перспективно для дальнейшего ветвления, если со-
ответвующее ему решение нецелочисленно.

4.1. СХЕМА МЕТОДА ВЕТВЕЙ И ГРАНИЦ 93
Ветвление.
Пусть x
k
i
j
-нецелочисленная компонента x
k
i
. Строим множества
G
(k)
ν
1
= {x|x ∈ G
(k)
ν
, x
i
j
≤ [x
k
i
j
]};
G
(k)
ν
2
= {x|x ∈ G
(k)
ν
, x
i
j
≥ [x
k
i
j
] + 1};
Решая задачу линейного программирования (4.1.1)-(4.1.3) на множествах G
(k)
ν
1
, G
(k)
ν
1
,
получаем соответствующие оптимальные решения x
1
1
, x
1
2
. Если оптимальное решение –
целочисленно, то соответствующее множество является граничным. Все множества, не
подвергавшиеся ветвлению, переобозначаем G
(k+1)
1
, . . . , G
(k+1)
s
.
Полагаем: ε
j
= ε(G
(k+1)
j
) = [(f(x
(k+1)
1
)].
Находим такое множество G
(k+1)
i
на котором выполняется: ε(G
(k+1)
i
) = min
j=
1,s
{ε(G
(k+1)
j
)}.
Предположим, что ε = ε(G
(k+1)
p
), тогда если G
(k+1)
p
– граничное множество, то решение
x
k+1
p
– оптимально, если нет, тогда переходим на итерацию (k+2) и.т.д.
4.1.2 Пример
Решить методом ветвей и границ задачу целочисленного линейного программирования.
max z = max(5x
1
+ 3x
2
);
3x
1
+ 5x
2
≤ 15,
5x
1
+ 2x
2
≤ 10,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
—целые.
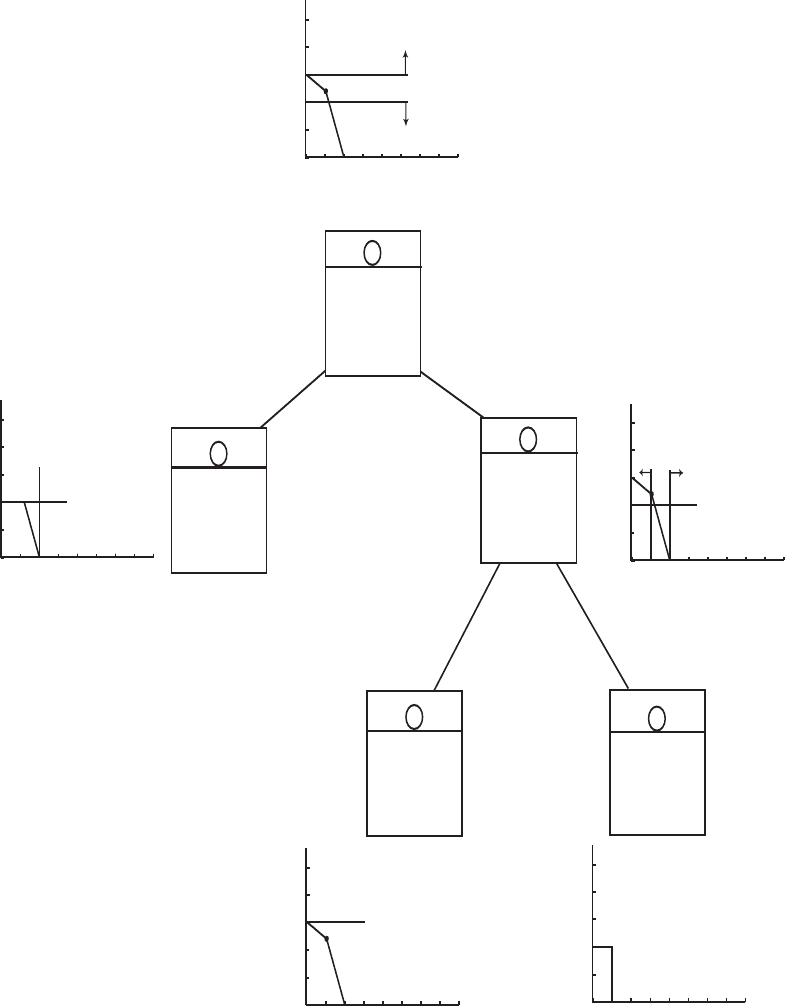
На рис. 4.1.7 изображена совокупность порожденных подзадач в виде дерева. Рассмот-
рим процесс построения этого дерева ветвления подробнее.
Исходной является вершина 1, в которой сформулированная за дача решается как за-
дача линейного программирования. Мы использовали для решения графический метод,
в общем случае используется симплекс-метод и его модификации. Оптимальное решение
достигается в точке с координатами x
1
= 1
1
19
и x
2
= 2
7
19
, z = 12
7
19
.

94 Глава 4. ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ
1
z=12 7/19
x
1
=1 1/19
x =2 7/19
2
1 2 3 4 5 6 7 8
0
1
2
3
4
5
Рис 4.1.2. Решение подзадачи один.
Так как обе переменные принимают нецелочисленные значения, любая из них может
быть выбрана в качестве переменной, инициирующей процесс ветвления. Выбор перемен-
ной x
2
порождает две подзадачи, связанные с условиями x
2
≤ 2 и x
2
≥ 3 соответственно
(из подзадачи один мы имеем x
2
= 2
6
17
, поэтому [x
∗
2
] = 2), а именно подзадачи 2 и 3.
Порожденные подзадачи содержат все допустимые целочисленные решения исходной
задачи, т.е. исходное множество допустимых целочисленных решений остается неизмен-
ным в процессе ветвления.
На следующем шаге осуществляется выбор одной из подзадач 2 или 3 для решения
и при необходимости для дальнейшего ветвления. Важно отметить, что не существует
точных способов реализации указанного выбора. Выбор различных альтернатив приво-
дит к разным последовательностям подзадач и, следовательно, к различному количеству
итераций, обеспечивающих получение оптимального целочисленного решения.
Продемонстрируем этот факт, пользуясь рис. 4.1.7. Предположим, что в первую оче-
редь рассматривается вершина 2 (x
2
≤ 2). Оптимальное решение соответствующей за-
дачи ЛП достигается в точке с координатами x
1
= 1
1
5
и x
2
= 2, z = 12. (Это решение
получено путем добавления ограничения x
2
≤ 2 к подзадаче 1).
2
z=12
x
1
=1 1/5
x =2
2
1 2 3 4 5 6 7 8
0
1
2
3
4
5
Рис 4.1.3. Решение подзадачи два.
Так как значение x
1
= 1
1
5
продолжает оставаться нецелочисленным, следовательно
два дополнительных условия x
1
≤ 1 и x
1
≥ 2 в задаче 2 порождают подзадачи 3 и

4.1. СХЕМА МЕТОДА ВЕТВЕЙ И ГРАНИЦ 95
4. Опять предположим, что сначала мы рассматриваем вершину 3. Подзадача 3 имеет
целочисленное решение z = 11 при x
1
= 1 и x
2
= 2.
1 2 3 4 5 6 7 8
3
z=11
x
1
=1
x =2
2
0
1
2
3
4
5
Рис 4.1.4. Решение подзадачи три.
Хотя задача 3 имеет целочисленное решение это не означает, что найден оптимум
исходной задачи. Поскольку имеются еще не решенные подзадачи 4 и 5, которые могут
улучшить целочисленное решение z = 11. Целочисленное решение подзадачи 3 опре-
деляет нижнюю границу z = 11 значений целевой функции. Нет необходимости рас-
сматривать те последующие подзадачи, для которых оптимальные значения z меньше
указанной нижней границы.
Решим подзадачу 4 (полученной путем введения неравенства x
1
≥ 2 в систему огра-
ничений задачи 2), находим ее оптимальное решение z = 10, x
1
= 2 и x
2
= 0. Полученное
решение целочисленное, но не превышает значения z = 11, следовательно нам оно не
подходит.
1 2 3 4 5 6 7 8
4
z=9
x
1
=0
x =3
2
0
1
2
3
4
5
Рис 4.1.5. Решение подзадачи четыре.
На следующем шаге нужно исследовать подзадачу 5, которая получается путем до-
бавления неравенства x
2
≥ 3. Для этой подзадачи оптимальным будет решение с z = 9,
x
1
= 0 и x
2
= 3. Решение подзадачи 5 целочисленно, но меньше чем решение подзадачи
3, z = 11.
96 Глава 4. ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ
5
z=10
x
1
=2
x =0
2
1 2 3 4 5 6 7 8
0
1
2
3
4
5
Рис 4.1.6. Решение подзадачи пять.
Эта информация получена путем рассмотрения вершин 1, 2, 3, 4 и 5 в порядке 1 →
2 → 4 → 3 → 5. (Можно прийти к такому же выводу, если сначала исследовать вершину
5, а не вершину 3. ) Заметим, что при движении по цепочке подза дач (1 → 5 → 2 →
3 → 4) в вершине 5 мы не имеем сведений о качестве полученного ранее решения, пока
не решим подзадачи 2, 3 и 4. По этой причине нельзя предсказать, выбор какой ветви
x
2
≥ 3 или x
2
≤ 2, осуществленный в вершине 1, является более выгодным.
Необходимо добавить, что в том случае, если в какой-то подзадаче, полученное реше-
ние превышает текущую нижнюю оценку не более чем на единицу, то такую подзадачу
не с ледует подвергать ветвлению. Поскольку в результате ветвления такой подзадачи мы
получим целочисленное решение равное, полученной ранее оценке. Продолжать ветвле-
ние имеет смысл только в том случае, если стоит задача найти все одинаковые целочис-
ленные решения.
4.1. СХЕМА МЕТОДА ВЕТВЕЙ И ГРАНИЦ 97
1 2 3 4 5 6 7 8
0
1
2
3
4
5
1
z=12 7/19
x
1
=1 1/19
x =2 7/19
2
1 2 3 4 5 6 7 8
0
1
2
3
4
5
2
z=12
x
1
=1 1/5
x =2
2
1 2 3 4 5 6 7 8
0
1
2
3
4
5
3
z=11
x
1
=1
x =2
2
1 2 3 4 5 6 7 8
0
1
2
3
4
5
4
z=9
x
1
=0
x =3
2
1 2 3 4 5 6 7 8
0
1
2
3
4
5
5
z=10
x
1
=2
x =0
2
Рис 4.1.7. Метод ветвей и границ ЗЛЦП.
98 Глава 4. ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ
4.1.3 Задачи для самостоятельного решения
4.1.1 4.1.2 4.1.3
max z = max(x
1
+ 4x
2
);
2x
1
+ 4x
2
≤ 17,
10x
1
+ 3x
2
≤ 15,
x
1
≥ 0.x
2
≥ 0,
x
1
, x
2
∈ Z
max z = max(x
1
+ 2x
2
);
2x
1
+ 2x
2
≤ 7,
4x
1
− 5x
2
≤ 9,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
max z = max(6x
1
+ 8x
2
);
3x
1
+ 5x
2
≤ 11,
4x
1
+ x
2
≤ 8,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
4.1.4 4.1.5 4.1.6
max z = max(6x
1
+ 8x
2
);
3x
1
+ 5x
2
≤ 12,
4x
1
+ x
2
≤ 10,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
max z = max(x
1
+ 4x
2
);
2x
1
+ 4x
2
≤ 7,
10x
1
+ 3x
2
≤ 15,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
max z = max(x
1
+ 2x
2
);
5x
1
+ 7x
2
≤ 21
−x
1
+ 3x
2
≤ 8,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
4.1.7 4.1.8 4.1.9
max z = max(x
1
+ x
2
);
6x
1
+ 5x
2
≤ 20,
2x
1
+ 3x
2
≤ 10,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
max z = max(x
1
+ 2x
2
);
2x
1
+ 9x
2
≤ 36,
x
1
+ x
2
≤ 7,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
max z = max(8x
1
+ 6x
2
);
2x
1
+ 5x
2
≤ 11,
4x
1
+ x
2
≤ 10,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
4.1.10 4.1.11 4.1.12
max z = max(x
1
+ x
2
);
2x
1
+ x
2
≤ 18
x
1
+ 2x
2
≤ 16,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
max z = max(x
1
+ x
2
);
x
1
+ 2x
2
≤ 10,
x
1
+ 2x
2
≥ 2,
2x
1
+ x
2
≤ 10,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
max z = max(2x
1
+ x
2
);
2x
1
+ 3x
2
≤ 12,
4x
1
+ x
2
≥ 10,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
4.1.13 4.1.14 4.1.15
max z = max(2x
1
+ 3x
2
);
x
1
+ 4x
2
≤ 14,
2x
1
+ 3x
2
≤ 12,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
max z = max(x
1
+ x
2
);
3x
1
+ 2x
2
≤ 5
x
2
≤ 2,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
max z = max(x
1
+ x
2
);
20x
1
+ 10x
2
≤ 75,
12x
1
+ 7x
2
≤ 55,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
4.1. СХЕМА МЕТОДА ВЕТВЕЙ И ГРАНИЦ 99
4.1.16 4.1.17 4.1.18
max z = max(2x
1
+ 3x
2
);
5x
1
+ 7x
2
≤ 35,
4x
1
+ 9x
2
≤ 36,
x
1
, x
2
≥ 0,
x
i
—целые.
min z = min(5x
1
− 3x
2
);
3x
1
+ 2x
2
≥ 6,
2x
1
− 3x
2
≥ −6,
x
1
− x
2
≤ 4,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
min z = min(6x
1
+ 4x
2
);
3x
1
+ x
2
≥ 3
x
1
− x
2
≥ 1,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
4.1.19 4.1.20 4.1.21
max z = max(2x
1
+ x
2
);
2x
1
+ 3x
2
≤ 11,
4x
1
+ x
2
≤ 10,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
max z = max(x
1
+ x
2
);
2x
1
+ 11x
2
≤ 38,
x
1
+ x
2
≤ 7,
4x
1
− 5x
2
≤ 5,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
min z = min(4x
1
+ 4x
2
);
2x
1
+ x
2
≤ 5,
2x
1
+ x
2
≤ 9,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
4.1.22 4.1.23 4.1.24
min z = min(2x
1
− x
2
);
2x
1
+ x
2
≤ 8
x
1
+ 3x
2
≥ 6,
3x
1
+ x
2
≥ 3,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
max z = max(x
1
+ x
2
);
6x
1
+ 5x
2
≤ 20,
2x
1
+ 3x
2
≤ 10,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
min z = min(6x
1
+ 4x
2
);
2x
1
+ x
2
≥ 3,
x
1
− x
2
≤ 1,
4x
1
− 5x
2
≤ 5,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
4.1.25 4.1.26 4.1.27
max z = max(8x
1
+ 2x
2
);
x
1
− 4x
2
≤ 4,
−4x
1
+ x
2
≤ 4,
x
1
− x
2
≤ 6,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
min z = min(2x
1
+ 3x
2
);
x
1
+ 2x
2
≥ 16
2x
1
+ 1x
2
≥ 18,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
min z = min(6x
1
+ 4
2
);
2x
1
+ 1x
2
≥ 3,
x
1
− 2x
2
≤ 2,
3x
1
+ 2x
2
≥ 1,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
4.1.28
max z = max(x
1
− 4x
2
);
2x
1
+ 3x
2
≤ 9,
2x
1
+ x
2
≤ 6,
x
1
≥ 0, x
2
≥ 0,
x
1
, x
2
∈ Z
100 Глава 4. ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ
4.2 Задача о коммивояжере
Постановка задачи. Имеется n городов A
1
, A
2
, . . . , A
n
. Задана матрица C издержек,
которые коммивояжер несет при переезде из города i в город j (c
ij
6= c
ji
). Необходимо
отыскать замкнутый маршрут (цикл), проходящий через все города только по одному
разу с наименьшими издержками, то есть построить цикл t = ((i
1
, i
2
), (i
2
, i
3
), . . . , (i
n
, i
1
)).
Суммарные издержки по циклу t вычисляются по формуле:
L(t) =
X
(i,j)∈t
c
ij
.
4.2.1 Алгоритм
1. Приведение матрицы. Пусть h
i
= min
j
c
ij
, c
1
ij
= c
ij
− h
i
, h
j
= min
i
c
1
ij
. Полагаем
c
0
ij
= c
1
ij
− h
j
.
Здесь h
i
, h
j
− приводящие константы строк и столбцов. Процесс приведения позво-
ляет из любой неотрицательной матрицы C = c
ij
получить матрицу C
0
= c
0
ij
, которая
обладает тем свойством, что в каждой ее строке и столбце имеется по крайней мере один
ноль.
Обозначим через H =
P
i
h
i
+
P
j
h
j
сумму приводящих констант, которая является
нижней оценкой длины всех возможных циклов.
Теорема 4.2.1 Оптимальный план задачи о коммивояжере с матрицей C
0
является
оптимальным и для задачи о коммивояжере с матрицей C. Если L(t) издержки цикла
t для матрицы C, а L
0
(t) издержки цикла t для матрицы C
0
, то L(t) = L
0
(t) + H.
2. Ветвление. Матрица C
0
задает множество всех замкнутых маршрутов G
0
. Метод
ветвей и границ позволяет разбить множество G
0
на два множества G
1
1
и G
1
2
, удовлетво-
ряющих условиям:
G
0
= G
1
1
[
G
1
2
, G
1
1
\
G
1
2
= ∅
Множеству G
1
1
принадлежат только те циклы, для которых из города i
∗
непосред-
ственно можно попасть в город j
∗
. Для циклов, принадлежащих G
1
2
переезд из i
∗
в j
∗
возможен только через промежуточный город.
Выбор пары (i
∗
, j
∗
) основан на следующих соображениях: рассматриваются элементы
матрицы C
0
, для которых c
ij
= 0 (переезд с наименьшими издержками). Таких элементов
