Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах

Подождите немного. Документ загружается.

331

MxpD xMp

*****==-

∑∑

,();

М(ξ), D(ξ) — числовые характеристики СВ ξ с выборкой

(х

, х

, ..., х

) ⇒ М(ξ) ≈ М*, D(ξ) ≈ D*

О: Доверительный интервал

(Θ* - ∆, Θ* + ∆) ⇔ Р(|Θ - Θ*| ≤ ∆) = γ,

∆ — точность оценки Θ* параметра Θ в функции распределения

F(x, Θ) СВ ξ, γ — коэффициент доверия

Для нормального распределения с параметрами m, σ при

m ≈ M* ⇒ P(m* - ∆ ≤ m ≤ m * + ∆) = 2Ф(∆

/σ). Для двумер-

ной СВ ζ = (ξ, η) с выборкой ((x

, y

), (x

, y

), ..., (x

, y

)) выбо-

рочный коэффициент корреляции

MMM

***

(, )

() () ()

() ()

,ξη

ξη ξη

ξη

⋅- ⋅

⋅

*()ξη⋅=

∑

36.3. Проверка статистических гипотез

Выдвинуты гипотезы о параметрах распределения:

: M(ξ) = M(η); H

: M(ξ) > M(η), где ξ, η — нормальные ге-

неральные совокупности, выборки из них объемами n и l имеют

выборочные средние m

*, m

*, дисперсии D*(ξ), D *(η), n ≥ 30,

l ≥ 30. В качестве критерия выбирается

Zm mDnD l=- +

ξη****() () ,

строится правосторонняя критическая область P(Z > Z

кр.пр

) = α,

α — уровень значимости (малая вероятность ошибочно отвергнуть

кр.пр













При вычисленном по выборкам

набл

> Z

кр.пр

гипотеза H

отвергается и принимается H

Выдвинута гипотеза Н

о функции распределения F(x) =

= P(ξ < x) СВ ξ при выборке (х

, х

, ..., х

) и построенном статис-

тическом ряде по интервалам (a

i-1

, a

il= 1,

— мера расхождения

между m

и np

— теоретические вероятности):

χ*

∑

()

mnp

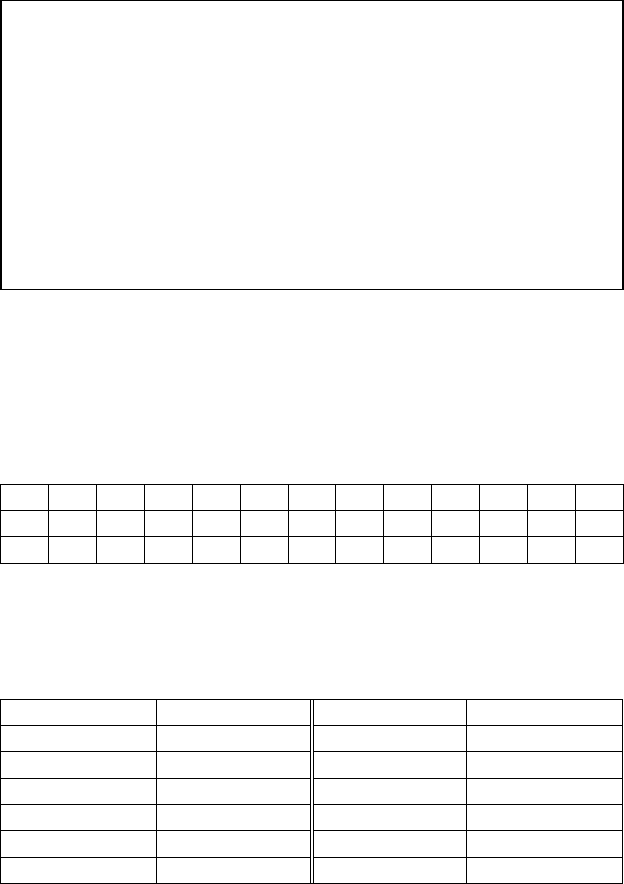
Т. (Пирсона):

Px xx

() () ,χϕ*d

<→

→∞

∫

где ϕ

(x) — плотность распределения χ

с k = l - 1 степенями сво-

боды 

332

Критерий согласия Пирсона:

1) выбирается уровень значимости α, равный вероятности того,

что Н

будет ошибочно отвергнута;

2) из уравнения

Pxx

()()χχ ϕα

>= =

∞

∫

определяется χ

— предел значимости (для определения χ

пользу-

ются таблицей);

3) при χ*

> χ

гипотеза Н

отвергается, при χ*

≤ χ

опытные

данные совместимы с гипотезой Н

Задачи к разд. 36

Задача 1. Измерен диаметр у 270 валов хвостовика. Величины

измеренных диаметров оказались в диапазоне 66–90 см. Разбив

диапазон на интервалы длиной в 2 см, подсчитали частоту m

по-

падания диаметра в данный интервал (см. таблицу):

№ 1 2 3 4 5 6 7 8 9 10 11 12

d, см

66–68 68–70 70–72 72–74 74–76 76–78 78–80 80–82 82–84 84–86 86–88 88–90

4 12 24 41 50 53 39 26 13 5 2 1

Построить гистограмму и эмпирическую функцию распределе-

ния.

Решение: Вычисляя относительные частоты по формуле р

* =

= m

/m, получим статистический ряд по интервалам:

d, см р* d, см р*

66–68 0,015 78–80 0,144

68–70 0,045 80–82 0,096

70–72 0,090 82–84 0,048

72–74 0,152 84–86 0,019

74–76 0,185 86–88 0,007

76–78 0,196 88–90 0,003

причем

∑

Эмпирическая функция распределения F(x) опре-

деляется по формуле ОК, разд. 36.1:

333

()

,, ,

≤

≤≤

068

0015 68 70

0060 70 72

0150 72 74

030227476

0487 76 78

0683 78 80

0827 80 82

0923

,, ,

≤≤

,,,

,, ,

82 84

0971 84 86

0 990 86 88

0 997 88 90

190

≤≤

x ..











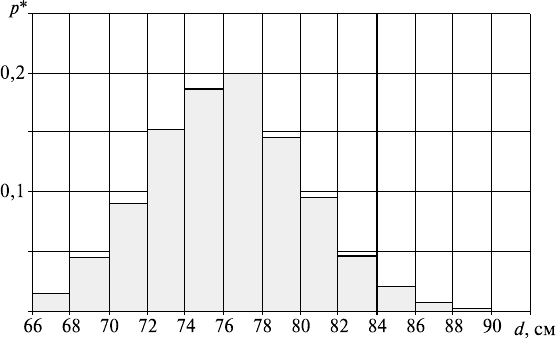
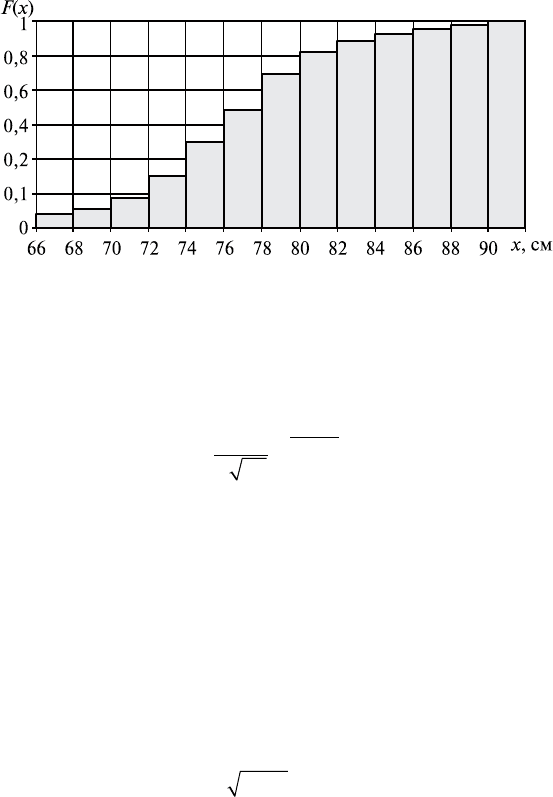
Гистограмма и эмпирическая функция распределения изобра-

жены на рис. 36.1 и рис. 36.2 соответственно.

Рис. 36.1

334

Рис. 36.2

Задача 2. Используя данные задачи 1 и гистограмму, делаем

предположение о нормальном законе распределения значений

диаметра. Найти параметры этого распределения.

Решение: Плотность вероятности нормального распределения

задается формулой

σπ

() .

()

По формулам ОК, разд. 36.2, имеем:

mM xp

DxMp xp

≈=

≈= -=-

∑

∑∑

***

**** **

;

() (σ MM *).

Выбирая в качестве x

* середины интервалов, получим

m = 67 ⋅ 0,015 + 69 ⋅ 0,045 + 71 ⋅ 0,090 + 73 ⋅ 0,152 +

+ 75 ⋅ 0,185 + 77 ⋅ 0,186 + 79 ⋅ 0,144 + 81 ⋅ 0,096 +

+ 83 ⋅ 0,048 + 85 ⋅ 0,019 + 87 ⋅ 0,007 + 89 ⋅ 0,003 = 76,21;

= (67)

⋅ 0,015 + (69)

⋅ 0,045 + ... + (89)

⋅ 0,003 -

- (76,21)

= 16,47,

16 47 406≈=,,.

Задача 3. Среднее значение расстояния до ориентира, получен-

ное по четырем независимым измерениям, равно 2250 м. Среднее

квадратическое отклонение для измерительного прибора σ = 40 м.

Систематическая ошибка отсутствует. Найти с надежностью 95%

доверительный интервал для измеряемой величины.

Решение: Так как случайные ошибки подчиняются нормальному

закону распределения, воспользуемся формулой ОК, разд. 36.2:

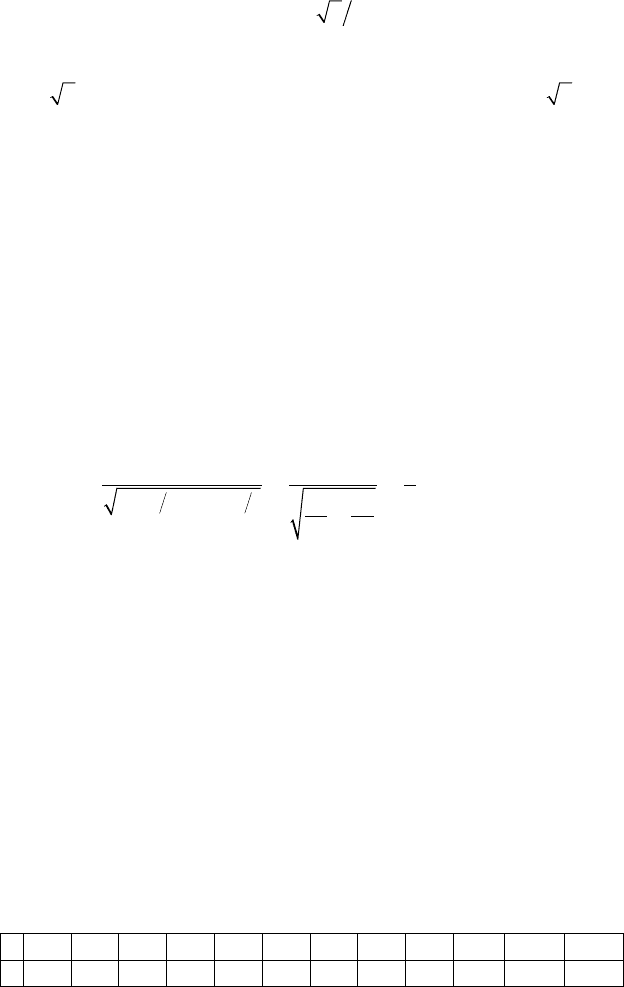
335

pm mm n()(),**-≤ ≤+=∆∆F∆2 σ

где Ф(x) — функция Лапласа; ∆ — точность оценки; m* — среднее

значение m. Из условий задачи известно, что m* = 2250, n = 4,

2Ф(∆

/σ) = 0,95. По таблице Приложения 1 имеем (∆

/σ) =

= 1,96, т.е. ∆ = 1,96 ⋅ 40/2 = 39,2 (м), m* - ∆ = 2250 - 39,2 =

= 2210,8 (м), m* + ∆ = 2250 + 39,2 = 2289,2 (м). Доверительный

интервал (2210,8–2289,2) покрывает истинное значение расстоя-

ния до ориентира с точностью 0,95.

Задача 4. По выборке ξ объемом n = 30 найден средний вес

* = 130 г изделий, изготовленных на первом станке; по выборке

η объемом l = 40 найден средний вес m

* = 125 г изделий, изготов-

ленных на втором станке, причем случайные величины ξ и η рас-

пределены нормально. Генеральные дисперсии этих величин из-

вестны: D(ξ) = 60 г

, D(η) = 80 г

. Требуется при уровне значимо-

сти 0,05 проверить нулевую гипотезу Н

: M(ξ) = M(η).

Решение: Найдем наблюдаемое значение критерия Z (ОК,

разд. 36.3):

DnDl

набл

|* *|

ξη

ξη() ()

130125

Критическая область в этом случае двусторонняя (-Z

кр

, Z

кр

При Z

набл

∈ (-Z

кр

, Z

кр

) принимается гипотеза Н

. Найдем

кр

= Ф

-1

((1 - 0,05)/2) = 1,96 по таблице функции Лапласа Ф(х).

Так как Z

набл

> Z

кр

, то Н

отвергается и принимается гипотеза Н

Задача 5. На автоматической линии, работающей 12 часов, про-

водились наблюдения над случайной величиной ξ — моментом

отказа линии (500 наблюдений). Проверить согласованность тео-

ретического и эмпирического законов распределения случайной

величины по критерию χ

Пирсона при уровне значимости

α = 0,05.

Решение: 1) Выдвигаем гипотезу: распределение случайной ве-

личины ξ является равномерным на интервале [0, 12].

2) Разбиваем [0, 12] на 12 интервалов и определяем частоту

попадания ξ в эти интервалы:

(0, 1) (1, 2) (2, 3) (3, 4) (4, 5) (5, 6) (6, 7) (7, 8) (8, 9) (9, 10) (10, 11) (11, 12)

m 41 34 54 39 49 45 41 33 37 41 47 49

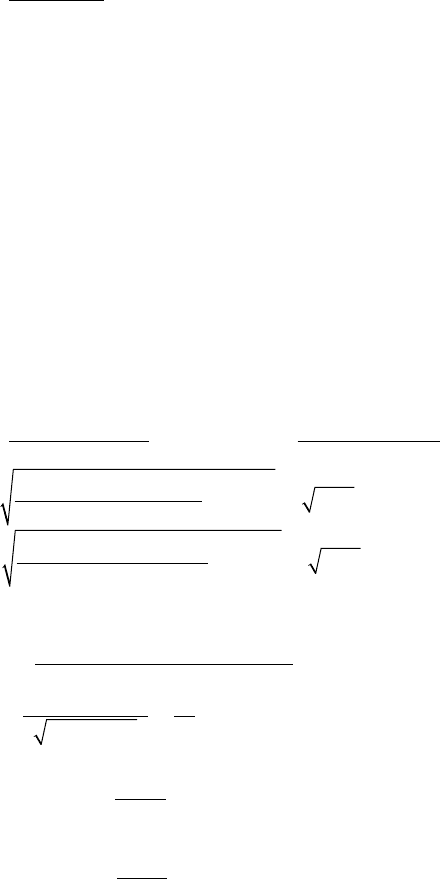
336

3) Находим χ*

по формуле ОК, разд. 36.3:

χ*

∑

()

mnp

где n = 500, p

= 1/12 по выдвинутой гипотезе о равномерном

распределении. Тогда имеем χ*

= [(41 - 500/12)

+ (34 -

- 500/12)

+ ... + (49 - 500/12)

] ≈ 10.

4) Находим число степеней свободы k = 12 - 1 = 11 и по таб-

лице χ*

(Приложение 2) при уровне значимости α = 0,05 находим

= 19,67.

5) Так как χ*

< χ

, то гипотезу можно принять.

Задача 6. По одной и той же теме проведены две контрольные

работы. Выбранные пять студентов получили следующие оценки.

Первая контрольная: 3, 4, 5, 3, 3; вторая контрольная: 2, 4, 4, 3, 4.

Найти коэффициент корреляции между оценками и прямые ре-

грессии.

Решение: Найдем средние арифметические и средние квадрати-

ческие отклонения выборки (ξ, η) = ((3, 2), (4, 4), (5, 4),

(3, 3), (3, 4)):

M *() ,;ξ=

+ +++

34533

M *() ,;η=

++++

24234

σξ*() (, ),;=

+ +++

34533

36 064

2 2222

ση*() (, ),.=

++++

24434

34 064

22222

Находим далее, используя формулы ОК, разд. 36.2, M*(ξ, η) и

коэффициент корелляции R*(ξ, η):

M *() ,;ξη⋅=

⋅+⋅+⋅+⋅+⋅

32 44 54 33 34

12 6

R*(, )

,,,

,.ξη =

-⋅

⋅

=≈

12 63634

064064

Прямая регрессии ξ на η имеет уравнение

xM RyM-= -**

*() (, )

()

(()),ξξη

σξ

ση

т.е. x - 3,6 = 0,6(y - 3,4); прямая регрессии η на ξ — уравнение

yM RxM-= -**

*() (, )

()

(()),ηξη

ση

σξ

т.е. y - 3,4 = 0,6(x - 3,6).

337

Задачи для самостоятельного решения

1) При 100 определениях дальности получены результаты, на

основании которых построена следующая таблица:

80–110 110–140 140–170 170–200 200–230 230–260 260–290 290–320

2 5 16 24 28 18 6 1

а) построить гистограмму и эмпирическую функцию распреде-

ления; б) найти среднее арифметическое и дисперсию, написать

выражение закона распределения случайной величины.

2) Постоянная величина измерена 25 раз с помощью прибора,

систематическая ошибка которого равна нулю, а случайные ошиб-

ки распределены нормально со средним квадратическим отклоне-

нием σ = 10 см. Определить границы доверительного интервала

для заданной измеряемой величины при коэффициенте доверия

γ = 0,95, если среднее арифметическое М* = 100 м.

3) Произведен выбор 200 деталей из текущей продукции пре-

цизионного токарного автомата. Проверяемый размер деталей

измерен с точностью до 1 мкм. Составлен статистический ряд по

интервалам:

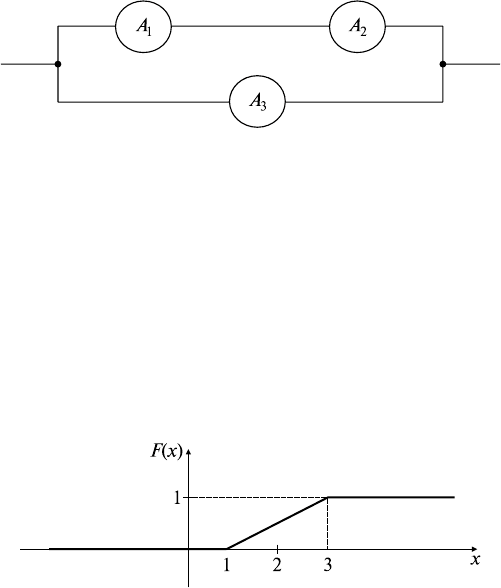
№ 1 2 3 4 5 6 7 8 9 10

(-20, -15) (-15, -10) (-10, -5) (-5, 0) (0, 5) (5, 10) (10, 15) (15, 20) (20, 25) (25, 30)

7 11 15 24 49 41 26 17 7 3

0,035 0,055 0,075 0,120 0,245 0,205 0,130 0,085 0,035 0,015

Оценить с помощью критерия χ

гипотезу о согласии выбороч-

ного распределения с законом нормального распределения при

уровне значимости α = 0,05.

4) По двум независимым выборкам n = 40, l = 50, извлечен-

ным из нормальных генеральных совокупностей ξ и η соответ-

ственно, найдены выборочные средние арифметические m

* = 130,

* = 140. Известны генеральные дисперсии D(ξ) = 80,

D(η) = 100. Требуется при уровне значимости 0,001 проверить

нулевую гипотезу Н

: M(ξ) = M(η) при конкурирующей гипотезе

: M(ξ) ≠ M(η).

338

Разные задачи

5) В ящике 4 новых и 6 старых инструментов. Рабочему выдали

3 инструмента. Найдите вероятность того, что: а) все выданные

инструменты старые; б) два из трех инструментов старые.

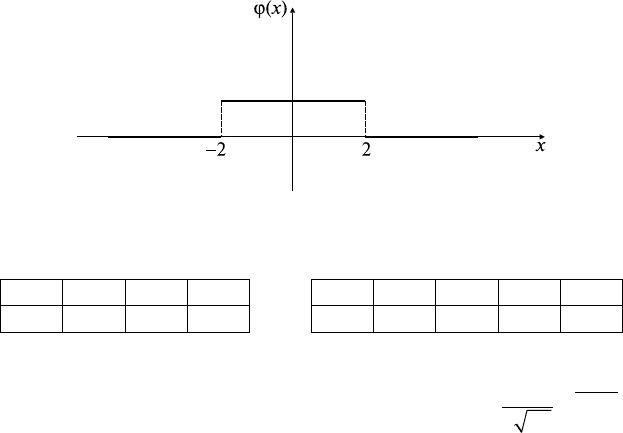
6) Элементы А

, А

электрической цепи работают независи-

мо друг от друга (рис. 36.3). Известны вероятности безотказной

работы элементов за время Т: Р(А

) = 0,6, Р(А

) = 0,8, Р(А

) = 0,7.

Найти вероятность безотказной работы системы за время Т.

Рис. 36.3

7) В магазин поступает продукция трех фабрик. Продукция

первой фабрики составляет 20%, второй — 45%, третьей — 35%

изделий. Известно, что средний процент нестандартных изделий

для первой фабрики равен 3%, для второй — 2%, для третьей — 4%.

Найти вероятность того, что оказавшееся нестандартным изделие

произведено на первой фабрике.

8) График функции распределения случайной величины ξ име-

ет вид, представленный на рис. 36.4. Найти математическое ожи-

дание М(2ξ + 3), дисперсию D(2ξ + 3).

Рис. 36.4

9) График плотности распределения случайной величины ξ

имеет вид, представленный на рис. 36.5. Найти математическое

ожидание М(2ξ + 1), дисперсию D(2ξ + 1), функцию распределе-

ния.

339

10) Даны случайные величины ξ и η:

0 1 2

-1 0 1 2

p 0,3 0,3 0,4 p 0,2 0,3 0,1 0,4

Найти М(ξ + η).

11) Случайная величина ξ задана формулой

()

Найти М(3ξ + 2), D(3ξ + 2).

12) По 100 парам проданной мужской обуви составлена эмпи-

рическая функция распределения

100

037

0043738

0143839

0293940

052

()

,, ,

≤

<≤

,,,

,, ,

40 41

0784142

0924243

143

<≤











Составить ряд распределения числа проданной продукции обу-

ви. Сколько обуви 39 размера было продано?

13) Случайная величина ξ распределена по нормальному зако-

ну с параметрами m, σ, причем наблюдаемые значения случайной

величины 35, 15, 5, 25, 5. Найти значение параметра m.

14) Случайная величина ξ распределена по показательному

закону с параметром λ. По результатам наблюдаемых значений 15,

5, 25, 35 этой случайной величины оценить параметр λ.

15) По данным измерений двух переменных построена таблица:

Рис. 36.5

340

9 1 12 5

6 4 7 3

Найти выборочный коэффициент корреляции и прямые регрес-

сии.

16) В ящике среди 100 фотокарточек находится одна разыски-

ваемая. Наудачу извлекли 10 фотокарточек. Найти вероятность

того, что среди них окажется нужная.

17) В сигнализатор поступили сигналы от двух устройств, при-

чем поступление каждого из сигналов равновозможно в любой

момент времени Т. Моменты поступления сигналов независимы

один от другого. Сигнализатор срабатывает, если разность между

моментами поступления сигналов меньше t (t < T). Найти веро-

ятность того, что сигнализатор срабатывает за время Т, если каждое

из устройств пошлет по одному сигналу.

18) В первой урне 4 белых и 8 черных шаров, во второй — 3 бе-

лых и 5 черных шаров. Из второй урны в первую переложили один

шар, а затем из первой урны вынули наугад один шар. Найти веро-

ятность того, что вынутый шар — белый.

19) В группе 20 юношей и 10 девушек. На 3 заданных препода-

вателем вопроса получены 3 ответа. Найти вероятность того, что

среди отвечавших два юноши и одна девушка.

20) Дана плотность распределения случайной величины ξ:

ϕ()

≤

-<≤











Найти функцию распределения.

21) Известно, что в одной из трех партий 2/3 деталей бракован-

ные, а в двух других — все доброкачественные. Для контроля про-

дукции наугад взята одна деталь. Найти вероятность обнаружения

бракованной продукции.

22) Дана функция распределения случайной величины ξ:

()

(),;

≤

-<≤











22 3

Найти математическое ожидание М(3ξ + 2).