Greenwood D.T. Advanced Dynamics
Подождите немного. Документ загружается.


349 Numerical stability
6.3 Numerical stability
One of the recurring problems in the numerical analysis of physical systems is that the
numerical results may show an instability which is not present in the physical system. The
stability of a numerical method depends on the step size h and on the stability characteristics
of the physical system. Other factors may influence the stability, including the numerical
methods used in representing constraints. In this section, we will consider the numerical
stability characteristics of various integration algorithms.
Euler integration
Consider first the relatively simple case of a single first-order differential equation
˙
y = f (y, t) (6.159)
The Euler algorithm is
y
n+1
= y
n
+ h
˙
y
n
(6.160)
The numerical stability is analyzed by the perturbation equation
δy
n+1
= δy
n
+ hf
n
δy
n
(6.161)
where we use the notation
f
n
≡
∂ f
∂y
(y
n
, t
n
) (6.162)
We consider (6.161) as a difference equation in δy and assume that f
n
varies slowly enough
that it can be assumed to be constant. Let
∂ f
∂y
= λ (6.163)
where λ is a real constant. Then (6.161) becomes
δy
n+1
− (1 + λh)δy
n
= 0 (6.164)
Now assume a solution of the form
δy
n
= Aρ
n
(6.165)
where A is a constant and ρ is the ratio δy
n+1
/δy
n
. From (6.164) and (6.165) we obtain
(ρ − 1 − λh)Aρ
n
= 0 (6.166)
We seek nonzero values of ρ in order to avoid trivial zero solutions for δy. Thus, we obtain
ρ = 1 + λh (6.167)
The necessary condition for numerical stability is that |ρ|≤1. The step size h is assumed
to be positive, and we see that −2 ≤ λh ≤ 0 for numerical stability.

350 Introduction to numerical methods
Now let us consider the more general case of a system of m first-order differential
equations which are to be integrated using the Euler method. We have
˙
y
i
= f
i
(y, t)(i = 1,...,m) (6.168)
The corresponding perturbation equations are
δ
˙
y
i
=
m
k=1
∂ f
i
∂y
k
δy
k
=
m
k=1
g
ik
δy
k
(i = 1,...,m) (6.169)
where g
ik
≡ ∂ f
i
/∂y
k
is assumed to be varying slowly enough to be considered constant
in the perturbation equations and the corresponding difference equations. Let us assume
solutions for δy of the form e
λt
. Then, for a single mode involving one value of λ,
d
dt
(δy
i
) = δ
˙
y
i
= λδy
i
(i = 1,...,m) (6.170)
From (6.169) and (6.170), upon setting the determinant of the coefficients of the δys equal
to zero, we obtain the characteristic equation
det |(g
ik
− λδ
ik
)|=0 (6.171)
where δ
ik
is the Kronecker delta. There are m eigenvalues (λs) which are real or occur in
complex conjugate pairs. The perturbation equations of the physical system are stable if all
the λs lie in the left half of the complex plane, that is, if they have negative real parts.
The Euler algorithm, when applied to the perturbation equations (6.170), results in dif-
ference equations of the form
δy
i(n+1)
= δy
in
+ λhδy
in
= (1 + λh)δy
in
(i = 1,...,m) (6.172)
where the first subscript indicates the state variable and the second subscript refers to the
time. This is consistent with (6.164) obtained earlier.
Let us assume solutions to (6.172) of the form
δy
in
= A
i
ρ
n
(6.173)
Then, we obtain
A
i
ρ
n+1
= (1 + λh) A
i
ρ
n
(6.174)
For each eigenvalue λ
j
,wehave
ρ
j
= 1 + λ
j
h ( j = 1,...,m) (6.175)
The necessary condition for stability is
|ρ
j
|≤1(j = 1,...,m) (6.176)
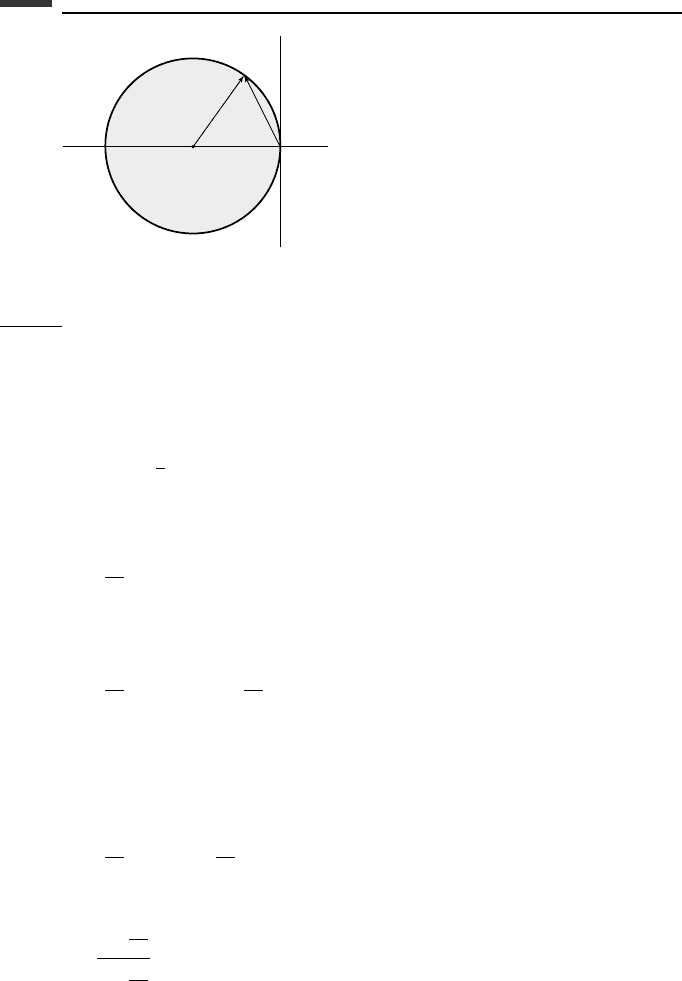
This result can be expressed conveniently as a plot of the stable region on the complex
plane, as shown in Fig. 6.3. If λ is real, then λh must lie in the range [−2, 0] for numerical
stability. On the other hand, if λ is imaginary, as it would be for an undamped second-order
system, then the Euler integration method is at least somewhat unstable, no matter how
small the step size.
351 Numerical stability
stable
−1
−2
λh - plane
λh
ρ
Figure 6.3.
Trapezoidal method
Let us consider the first-order system
˙
y = f (y, t) (6.177)
The trapezoidal algorithm is
y
n+1
= y
n
+
h
2
(
˙
y
n+1
+
˙
y
n
) (6.178)
Since
˙
y
n+1
is a function of y
n+1
,thisisanimplicit method and uses iteration.
The perturbation equation corresponding to (6.177) is
δ
˙
y =
∂ f
∂y
δy = λδy (6.179)
where we assume that λ can be considered to be constant. The trapezoidal algorithm applied
to the perturbation equation results in
1 −
λh
2
δy
n+1
−
1 +
λh
2
δy
n
= 0 (6.180)
Assume solutions of the form
δy
n
= Aρ
n
(6.181)
and substitute into (6.180). After dividing by Aρ
n
, the characteristic equation is
1 −
λh
2
ρ −
1 +
λh
2
= 0 (6.182)
or
ρ =
1 +
λh
2
1 −
λh
2
(6.183)

352 Introduction to numerical methods
Notice that λ is the real eigenvalue for the linearized perturbation equation, while ρ is the
corresponding stability parameter for the difference equation. There is numerical stability
if |ρ|≤1, and this will occur if the physical perturbations are stable, that is, if λ ≤ 0.
For the more general case where y in (6.177) is an m-vector, the m λs and the corre-
sponding m ρs are complex in general. Nevertheless, as was shown for the case of Euler
integration, the equation relating λ and ρ still applies. Thus, (6.183) is valid for each eigen-
value λ and the corresponding ρ.Ifλ = a + ib, for example, then
ρ =
1 +
ah
2
+ i
bh
2
1 −
ah
2
− i
bh
2
(6.184)
We see that |ρ| < 1fora < 0. In other words, if the physical system is stable and all its roots
are in the left half-plane, then the numerical representation using the trapezoidal method is
also stable for any step size h.
Runge–Kutta methods
Consider a first-order system whose perturbation equation has the form
δ
˙
y = λδy (6.185)
where λ is a constant. Referring to the RK-2 algorithm given by (6.89)–(6.92), we find that
δ
˜
y
n+
1
2
= δy
n
+
1
2
λhδy
n
(6.186)
δ
˜
˙
y
n+
1
2
= λδy
n
+
1
2
λ
2
hδy
n
(6.187)
δy
n+1
= δy
n
+ λhδy
n
+
1
2
(λh)
2
δy
n
=
1 +λh +
1
2
(λh)
2
δy
n
(6.188)
Now assume a solution of the form
δy
n
= Aρ
n
(6.189)
Upon substituting into (6.188) and dividing by Aρ
n
, we obtain
ρ = 1 + λh +
1
2
(λh)
2
(6.190)
For this system with λ real, the value of ρ is never negative, and ρ = 1forλh = 0, −2.
Thus, there is numerical stability for ρ ≤ 1orfor−2 ≤ λh ≤ 0.
Now consider the more general case in which δy is an m-vector, as in (6.170). Equation
(6.190) still applies in this case, but the λs and the corresponding ρs may be complex. In
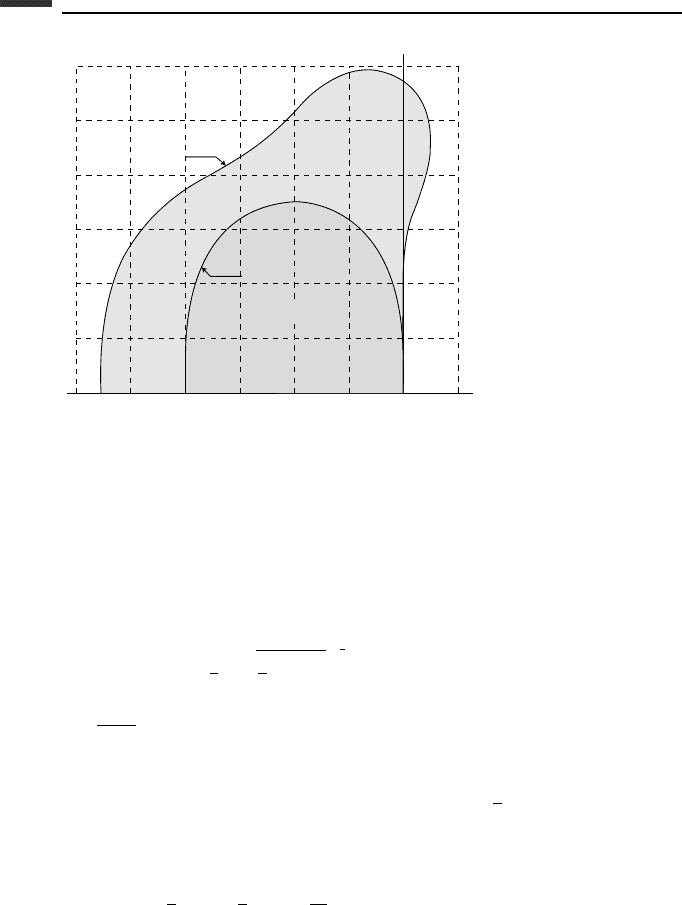
order to obtain the stability in the the complex λh-plane, we take |ρ|=1 and let
ρ = e
iφ
(6.191)
353 Numerical stability
λh – plane
RK – 4
3
2.5
2
1.5
1
0.5
a
–2.5
–2
–1.5
–0.5
0.5
0
–1
Stability boundaries λh = a + ib
–3
b
RK – 2
Stable
Figure 6.4.
Then we solve for λh as φ is varied. For example, suppose we assume
λh = a +ib (6.192)
and substitute into (6.190). By equating real and imaginary parts separately, we obtain the
following equations for a and b:
a =−1 ±
cos φ −
1
2
+
5
4
− cos φ
1
2
(6.193)
b =
sin φ
a + 1
(6.194)
The results are plotted in Fig. 6.4. For convenience, only the upper half of the complex
plane is shown. Note that the stability boundary for RK-2 is symmetric about the real axis
and also about the line a =−1. The maximum value of b is
√
3.
The stability boundary for the RK-4 algorithm is found by using a similar procedure. In
this case, we find that, in general,
ρ = 1 + λh +
1
2
(λh)
2
+
1
6
(λh)
3
+
1
24
(λh)
4
(6.195)
and, for a point on the stability boundary,
ρ = e
iφ
= cos φ + i sin φ (6.196)
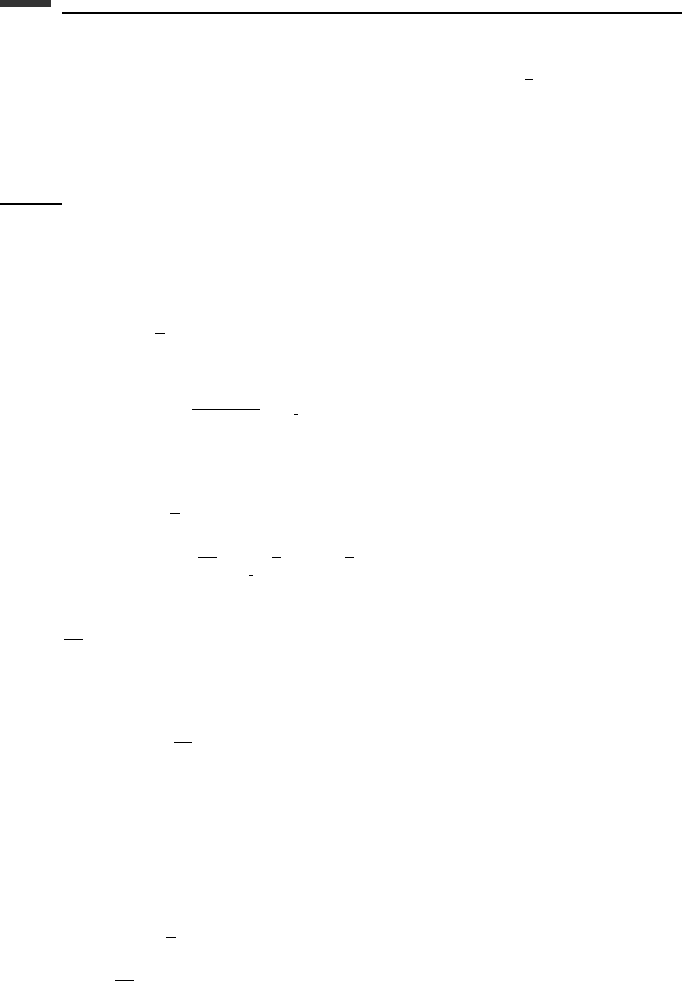
354 Introduction to numerical methods
It can be shown that, for real values of λh, there is numerical stability for −2.7853 ≤ λh ≤ 0.
Furthermore, for an imaginary value of λh, as might occur in the analysis of an undamped
second-order system, the stability boundary occurs at λh =±i2
√
2. From Fig. 6.4 it can
be seen that the RK-4 algorithm has a considerably larger region of numerical stability than
RK-2.
Midpoint method
Consider the second-order system
¨
y = f (y, t) (6.197)
The implicit algorithm applied to this system is
y
n+1
= y
n
+
h
2
(
˙
y
n+1
+
˙
y
n
) (6.198)
where
˙
y
n+1
=
˙
y
n
+ hf
y
n+1
+ y
n
2
, t
n+
1
2
(6.199)
We see that y
n+1
appears on both sides of the equation, implying an iterated solution.
The numerical stability is analyzed by considering the perturbation equations
δy
n+1
= δy
n
+
h
2
(
δ
˙
y
n+1
+ δ
˙
y
n
)
(6.200)
δ
˙
y
n+1
= δ
˙
y
n
+ h
∂ f
∂y
n+
1
2
1
2
δy
n+1
+
1
2
δy
n
(6.201)
Let us use the notation
∂ f
∂y
≡−k (6.202)
and assume that k varies slowly enough to be considered constant in the stability analysis.
Then (6.201) becomes
δ
˙
y
n+1
= δ
˙
y
n
−
hk
2
(δy
n+1
+ δy
n
) (6.203)
Now consider y and
˙
y as separate variables in the difference equations, and assume the
solutions
δy
n
= Aρ
n
(6.204)
δ
˙
y
n
= Bρ
n
(6.205)
A substitution into (6.200) and (6.203) yields
(ρ − 1) Aρ
n
−
h
2
(ρ + 1)Bρ
n
= 0 (6.206)
(ρ + 1)
hk
2
Aρ
n
+ (ρ − 1)Bρ
n
= 0 (6.207)
355 Numerical stability
Divide each equation by ρ
n
and set the determinant of the coefficients of A and B equal to
zero. The resulting characteristic equation is
1 +
h
2
k
4
ρ
2
+
h
2
k
2
− 2
ρ + 1 +
h
2
k
4
= 0 (6.208)
Assuming that k is positive, we obtain
ρ =
1 +
h
2
k
4
−1
1 −
h
2
k
4
± ih
√
k
(6.209)
Thus,
|ρ|
2
=
1 +
h
2
k
4
−2
1 −
h
2
k
4
2
+ h
2
k
= 1 (6.210)
We see that this iterative midpoint method is numerically stable for all h and positive k.
In addition to the numerical stability, one should also consider the convergence properties
of the iteration procedure. This procedure consists of evaluating
˙
y
n+1
and y
n+1
alternately,
using (6.198) and (6.199), meanwhile keeping constant y
n
and
˙
y
n
. We wish to determine
whether perturbations of y
n+1
will grow or diminish in amplitude in successive iterations.
From (6.200) and (6.201) we obtain
δy
( j +1)
n+1
= hδ
˙
y
n
−
h
2
k
4
δy
( j )
n+1
+
1 −
h
2
k
4
δy
n
(6.211)
where δ
˙
y
n
and δy
n
are set equal to zero. The superscript ( j)or(j + 1) refers to the iteration
number. We see that
δy
( j +1)
n+1
<
δy
( j )
n+1
if 0 < h
√
k < 2. Previously, we assumed that k is positive. If k is negative, the midpoint
method is numerically unstable for all positive values of step size h.
We conclude, then, that the convergence of the iteration procedure is critical in determin-
ing the range of h for overall numerical stability of the midpoint method.
Extraneous roots
When one uses higher-order algorithms such as Adams–Bashforth or Adams–Moulton, the
characteristic equation associated with the difference equations is of higher degree than
the characteristic equation obtained from the linearized differential equations describing
perturbations of the system. Thus, in addition to the roots approximating the true values,
there are additional extraneous roots introduced in the numerical solution. These extraneous
roots arise because the algorithms include values of the variables previous to time t
n
.
As a simple example, consider the AB-2 algorithm, namely,
y
n+1
= y
n
+
3
2
h
˙
y
n
−
1
2
h
˙
y
n−1
(6.212)
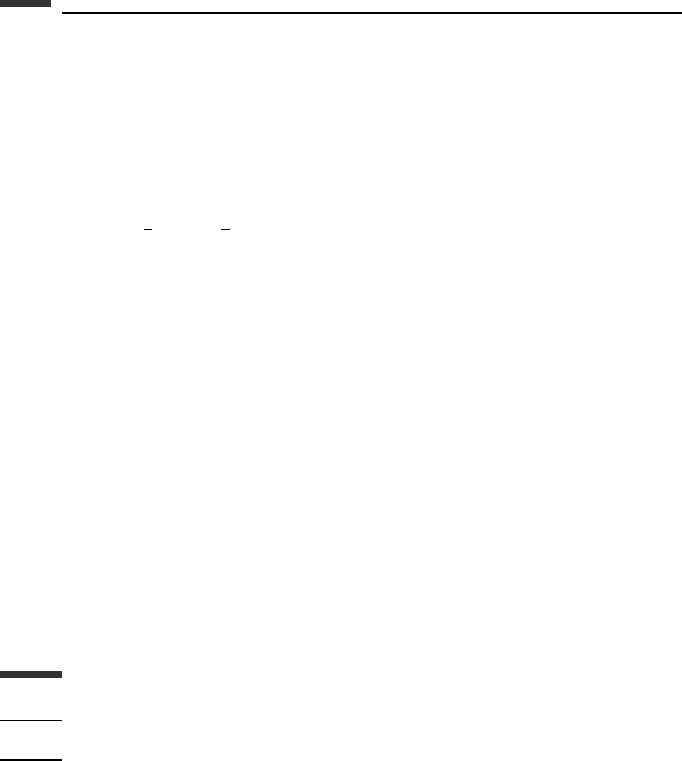
356 Introduction to numerical methods
Suppose we apply this algorithm to the first-order equation
˙
y = λy (6.213)
where λ is a constant. Assuming solutions of the form
y
n
= Aρ
n
(6.214)
the characteristic equation associated with (6.212) is
ρ
2
−
1 +
3
2
λh
ρ +
1
2
λh = 0 (6.215)
Assuming that λh is real, the AB-2 algorithm is numerically stable for −1 ≤ λh ≤ 0.
As a specific example, let λh =−0.1. The corresponding characteristic equation is
ρ
2
− 0.85ρ − 0.05 = 0 (6.216)
and the roots are ρ
1,2
= 0.9052, −0.0552. If the numerical procedure were exact, then we
should have ρ = e
λh
= 0.9048. Thus, we see that the root −0.0552 is extraneous.
As another example, let λh =−1 which is on the boundary of the stable region. The
characteristic roots in this case are ρ = 0.5, −1. The root −1 is on the stability boundary
and is extraneous. Thus, it is the extraneous root which causes numerical instability for
more negative values of λh.
In general, the number of extraneous roots is determined by the number of time increments
in the past at which data are used in the algorithm. For example, the AB-3 algorithm involves
˙
y
n−2
. This results in two extraneous roots for each variable, assuming first-order differential
equations.
For multiple-pass algorithms such as the various predictor–corrector methods, the algo-
rithm as a whole determines the number of extraneous roots. For example, the AB-3, AM-4
combination involves
˙
y
n−2
and will introduce two extraneous roots per variable.
6.4 Frequency response methods
Transfer functions
Consider a linear time-invariant system which has a sinusoidal input. The steady-state
output will be sinusoidal with the same frequency as the input but, in general, with a
different amplitude and phase. If one uses complex notation, the amplitude and phase of
the output relative to the input are expressed by the transfer function
G(i ω) = Me
iφ
(6.217)
where M(ω) is the relative amplitude and φ(ω) is the relative phase.
The system under consideration may be originally linear or may be a linearized system
which is represented by a set of perturbation equations. The data resulting from a numerical
integration of the linear equations can be considered to be samples taken from a continuous

357 Frequency response methods
output, albeit an output slightly in error compared to the true output. The transfer function
relating this computed output to the same sinusoidal input is of the form
G
∗
(iω) = M
∗
e
iφ
∗
(6.218)
where M
∗
and φ
∗
are functions of ω. Our problem is to find the relationship of G
∗
(iω)to
G(i ω) for some combination of linear equations and integration algorithm.
As a simple example, consider a pure integrator with a unit sinusoidal input. Its differential
equation can be written in the complex form
˙
y = e
iωt
(6.219)
Let us use the Euler integration algorithm and the discrete time
t
n
= nh (6.220)
We obtain the difference equation
y
n+1
= y
n
+ he
iωnh
(6.221)
The steady-state solution of this equation has the form
y
n
= G
∗
(iω)e
iωnh
(6.222)
where G
∗
(iω) is complex, in general. This solution is sinusoidal and of the same frequency
as the input, but G
∗
(iω) allows for a different amplitude and phase at the output y
n
.
If (6.222) is substituted into (6.221), we obtain
e
iωh(n+1)
− e
iωnh
G
∗
(iω) = he
iωnh
or
G
∗
(iω) =
h
e
iωh
− 1
(6.223)
Compare this result with that for the integrator of (6.219) where
G(i ω) =
1
iω
(6.224)
We see that one can obtain G
∗
(iω) from G(iω) by replacing iω with (e
iωh
− 1)/ h. This
substitution is valid for any transfer function G(iω) if Euler integration is used.
In general, if one knows the transfer operator G(s), where s is the Laplacian variable,
then one obtains G(i ω) by the substitution s = iω. G
∗
(iω) is obtained by letting s =
(e
iωh
− 1)/ h for the case of Euler integration.
As a second example, suppose we again consider an integrator with a sinusoidal input,
as given by (6.219), and use the RK-2 algorithm. The resulting difference equation is
y
n+1
= y
n
+ he
iωh(n+
1
2
)
(6.225)
Assume steady-state solutions of the form given by (6.222). We obtain
(e
iωh(n+1)
− e
iωhn
)G
∗
= he
iωh(n+
1
2
)
(6.226)
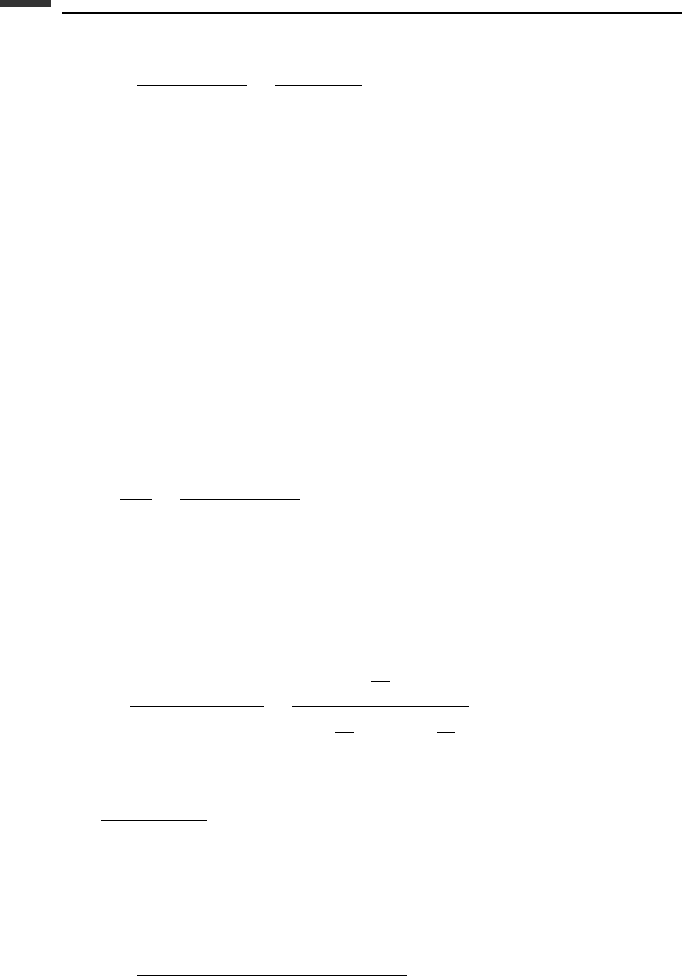
358 Introduction to numerical methods
which leads to
G
∗
(iω) =
h
e
iωh/2
− e
−iωh/2
=
h
i2 sin(ωh/2)
(6.227)
We note that as the step size h approaches zero, G
∗
(iω) approaches G(iω), as given by
(6.224).
It is important to realize that, for multiple-pass algorithms such as RK-2, one can no
longer obtain G
∗
(iω) by making the appropriate substituting for s in G(s). The form
of G
∗
(iω) is complicated by the presence of intermediate variables in making extra
passes.
Example 6.1 Consider a second-order system described by the differential equation
¨
y + 2ζω
n
˙
y + ω
2
n
y = f (t) (6.228)
where ω
n
is the undamped natural frequency and ζ is the damping ratio. Assuming that all
initial conditions are zero, the Laplace transform of this equation is
s
2
+ 2ζω
n
s + ω
2
n
Y (s) = F(s) (6.229)
This leads to
G(s) =
Y (s)
F(s)
=
1
s
2
+ 2ζω
n
s + ω
2
n
(6.230)
For a sinusoidal input,
f (t) = cos ωt (6.231)
the steady-state response is found by letting s = iω in (6.230) and obtaining the transfer
function
G(i ω) =
1
ω
2
n
− ω
2
+ i 2ζω
n
ω
=
1
ω
2
n
1 −
ω
ω
n
2
+ i 2ζ
ω
ω
n
(6.232)
Now consider a specific numerical example with ω
n
= 1, ω = 0.95, ζ = 0.5, and obtain
G =
1
0.0975 +i 0.95
= 1.047131∠ − 1.468523
where the latter form gives the amplitude and the phase angle in radians relative to the
sinusoidal input.
Suppose we solve this problem using Euler integration with a step size h = 0.01. If we
replace iω by (e
iωh
− 1)/ h in (6.232), we obtain
G
∗
(iω) =
h
2
(e
iωh
− 1)
2
+ 2ζω
n
h(e
iωh
− 1) + ω
2
n
h
2
(6.233)
