Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

379 Kinematic constraints

vector are expressed in terms of the same nonorthogonal components whose directions lie

along the normals to the constraint surfaces.

The qs, found by using (6.395), are

x = 2xC

+ C

(6.404)

y = 2yC

+ C

(6.405)

z =−

+ C

(6.406)

The velocity corrections are obtained by solving ﬁrst for the K s, using the equations



+ 4y





2x + 2y −



=−

(6.407)



2x + 2y −



+ 3K

=−

(6.408)

Then the K s are substituted into (6.372). The results are



x = 2xK

+ K

(6.409)



y = 2yK

+ K

(6.410)



z =−

+ K

(6.411)

A comparison of the numerical results obtained by using the Baumgarte method or the

one-step method of representing holonomic constraints shows that the one-step method is

much more accurate, although either method may be acceptable for a relatively small step

size. On the other hand, the two methods show about the same accuracy with respect to

the time response, as measured by the period. Time errors are determined primarily by

truncation errors associated with the integration algorithm.

One-step method for nonholonomic constraints

The procedure for applying the one-step method to systems with nonholonomic constraints

begins in the same way as with the Baumgarte method, except that the U s are set equal to

zero. Thus, assuming m nonholonomic constraints of the form

(q,

q, t) = 0(j = 1,...,m) (6.412)

one can write the dynamical equations as in (6.330), namely,



∂T

∂



−

∂T

∂q



j=1

∂g

∂

+ Q

(q,

q, t)(i = 1,...,n) (6.413)

Next, differentiate the constraint functions with respect to time, obtaining

(q,

q, t) = 0(j = 1,...,m) (6.414)

One can solve the n equations of (6.413) for the n

qs as functions of (q,

q,λ,t) and these

expressions are then substituted into (6.414), obtaining m equations which are linear in the

380 Introduction to numerical methods

λs. After solving these equations for λ

(q,

q, t), ( j = 1,...,m), we substitute back into

the

q expressions to obtain the ﬁnal dynamical equations of the form

(q,

q, t)(i = 1,...,n) (6.415)

At this point, we should explain that another method such as Maggi’s equation plus (6.414)

might be used in obtaining (6.415).

The n second-order dynamical equations can be converted to 2n ﬁrst-order equations

which are integrated numerically. At the end of each step, we wish to apply a one-step

correction to the solution. The fact that the system is nonholonomic results in an impor-

tant difference in the correction strategy, as compared to the holonomic case. Due to the

nonintegrable nature of the constraints, there is no direct way of detecting errors in the

conﬁguration, that is, the qs. On the other hand, for any given conﬁguration, velocity errors

result in a separation of the solution point from the constraint surface in velocity space.

These errors can be detected and corrections made to the

qs. Another reason for this ap-

proach is the fact that, at least for holonomic systems, errors in the

φs tend to be much

larger than conﬁguration errors as measured by the φs. In other words, the errors in the

tend to be larger than errors in the qs due to the smoothing effect of the integration process.

Our approach, then, will be to make one-step corrections in a manner similar to the velocity

corrections for holonomic constraints.

First, we require that the velocity correction vector be a linear combination of the indi-

vidual constraint gradient vectors in velocity space.





k=1

∂g

∂

(i = 1,...,n) (6.416)

Next, the corrections must exactly cancel the constraint errors, that is,



i=1

∂g

∂



=−g

( j = 1,...,m) (6.417)



i=1



k=1

∂g

∂

∂g

∂

=−g

( j = 1,...,m) (6.418)

These m equations are solved for the mKs and then the velocity corrections are made

using (6.416).

Example 6.6 Let us consider once again a nonholonomic system consisting of a dumb-

bell sliding on a horizontal plane and constrained by a knife edge at one of the particles

(Fig. 6.6). The nonholonomic constraint equation is

(q,

q) =−

x sin φ +

y cos φ = 0 (6.419)

381 Kinematic constraints

which states that the transverse velocity at particle 1 is equal to zero. Following the procedure

of Example 6.4 on page 370 for the case in which U = 0, we obtain the dynamical equations:

x =

cos φ −

φ sin φ(

x cos φ +

y sin φ) (6.420)

y =

sin φ +

φ cos φ(

x cos φ +

y sin φ) (6.421)

φ =−

(

x cos φ +

y sin φ) (6.422)

The equations are integrated numerically. At the end of each time step, the nonholonomic

constraint function g

is evaluated. From (6.418), we ﬁnd that

K (sin

φ + cos

φ) =−g

(6.423)

K =−g

(6.424)

Then, from (6.416), the one-step velocity corrections are



x =−g

sin φ (6.425)



y = g

cos φ (6.426)



φ = 0 (6.427)

Thus, at the end of each time step in the numerical integration, the value of the nonholonomic

constraint function is approximately zero.

A comparison of constraint enforcement methods

If the given holonomic and nonholonomic examples are analyzed numerically for typi-

cal cases, some observations and conclusions can be made. For the holonomic system of

Example 6.5 on page 376, the results are much more accurate for the one-step method than

for the Baumgarte method. This is particularly true of the velocities and amounts to about

two additional decimal digits of accurate data for the same step size, using the RK-2 algo-

rithm. The conﬁguration accuracy is also much superior for the one-step method, although

both methods show satisfactory accuracy for a relatively small step size. A comparison of

computing times shows that the one-step method requires about one-third more time for the

same step size.

If one compares the Baumgarte and one-step methods, as they are applied to nonholo-

nomic systems such as Example 6.6 on page 380, the one-step method again provides

superior accuracy. Both methods, however, exhibit some loss of accuracy for nonholo-

nomic constraints. This arises because there is no direct way of detecting conﬁguration

errors for nonholonomic systems as the computation proceeds.

A comparison of the solution accuracies of the two methods with respect to time shows

roughly the same accuracy. This occurs because time accuracy is not closely related to con-

ﬁguration accuracy. Rather, the time aspect of the computations, as indicated by the period

382 Introduction to numerical methods

of the motion, for example, is strongly inﬂuenced by the choice of the integration algorithm

and the step size. The truncation errors are the most important factor. For conservative

systems such as we have been studying, the overall accuracy can be improved by making

further corrections based on energy errors. These errors tend to appear as velocity errors

whose magnitudes increase with time. This affects the periods and other important charac-

teristics of the motion. The use of energy methods in improving computational accuracy

will be considered in Section 6.6.

Euler parameter constraints

The four Euler parameters (

,

,η) were introduced in Section 3.1 as generalized

coordinates to represent the orientation of a rigid body relative to some frame, usually an

inertial frame. Since a rigid body has only three rotational degrees of freedom, there must

be an equation of constraint relating the Euler parameters. It is the holonomic constraint

φ(

,

,η) = 

+ 

+ η

− 1 = 0 (6.428)

In accordance with (3.80), the Euler parameters are generated by the numerical integration

of four ﬁrst-order kinematical equations, namely,

˙

(ω



− ω



+ ω

η) (6.429)

˙

(ω



− ω



+ ω

η) (6.430)

˙

(ω



− ω



+ ω

η) (6.431)

˙η =−

(ω



+ ω



+ ω



) (6.432)

The body-axis angular velocity components (ω

,ω

) are obtained by the numerical

integration of the rotational equations of motion.

Let us use the one-step method to correct any constraint errors. First, calculate the gradient

vector in q-space at the operating point.

∇φ = [2

2

2η]

(6.433)

Next, we require the correction vector q to exactly compensate for the constraint error at

the end of each time step, that is,

∇φ · q =−φ (6.434)

where

q = C∇φ (6.435)

Thus, we take the correction vector in the direction of the gradient ∇φ. From (6.434) and

(6.435), the coefﬁcient C is

C =

−φ

∇φ ·∇φ

−φ





+ 

+ η



≈−

(6.436)

383 Energy and momentum methods

In detail, the corrections to the generalized coordinates are



=−



φ, 

=−



φ, 

=−



φ, η =−

ηφ (6.437)

Note that this correction q does not change the direction of the conﬁguration vector q in

4-space.

The correction of the Euler parameter values does not cause a risk of numerical instability

because, in the usual case of rigid body motion, the Euler parameter values do not enter the

dynamical equations. Thus, there is no need to set

φ or

φ equal to zero, thereby avoiding

tendencies toward numerical instability. Instead, the dynamical equations are written in

terms of quasi-velocities (ωs) and the Euler parameter calculations for the orientation are

performed separately.

6.6 Energy and momentum methods

In assessing the accuracy of numerically computed solutions of the equations of motion

of a dynamical system, it is helpful to have relatively simple check solutions available. A

common approach is to use integrals of the motion, that is, functions whose values remain

constant during the course of the solution, as checks on accuracy. For example, the energy

integral E = T

− T

+ V may be used for conservative systems. Other systems may have

one or more components of momentum or angular momentum conserved. Integrals of the

motion are particularly effective in detecting programming errors. Of course, these methods

are ineffective against errors in the values of the physical parameters.

Energy corrections

Let us consider a conservative system whose energy integral has the form

E(q,

q) = T

− T

+ V = E

(6.438)

At each time step in the numerical solution, we wish to correct for an energy error E

given by

E = E − E

(6.439)

where E

is evaluated from the initial conditions.

First let us note that, for a given conﬁguration and energy constant E

, the equation

E(q,

q) − E

= 0 (6.440)

represents a surface in n-dimensional velocity space (Fig. 6.9). Since the kinetic energy

function T (q,

q) is positive deﬁnite and quadratic in the

qs, the form of the energy surface

is ellipsoidal for the particular case of 3-space.

The velocity correction 

q will be taken in the direction normal to the energy surface,

that is, in the direction of the gradient ∇E or ∇T . In accordance with the one-step method,

384 Introduction to numerical methods

E−E

= 0

∆q

Figure 6.9.

let us assume that



q = K ∇T (6.441)

and choose the value of K such that

∇T · 

q =−E (6.442)

which results in the exact cancellation of the energy error. Thus, we obtain

K =

−E

(∇T )

=−E





j=1



∂T

∂





−1

(6.443)

The individual velocity corrections are



= K

∂T

∂

(i = 1,...,n) (6.444)

If the conservative system is subject to kinematic constraints, the corresponding constraint

surfaces in velocity space are typically planes passing through the origin. The velocity vector

q is constrained to lie in the common intersection of these planes. Any velocity correction

is taken in a direction normal to

q. But from Fig. 6.9 we see that the velocity correction 

for an energy error is approximately the same direction as

q. (It is exactly the same direction

if the energy surface is spherical.) Thus, the velocity corrections for constraint errors and

energy errors are approximately normal to each other and do not interact very strongly.

From (6.443) and (6.444), we see that 

q can be quite large if the magnitude of

q or

the generalized momentum vector is very small. For most dynamical systems, this will not

occur. But if the kinetic energy T

does attain a small value compared to its maximum during

the motion of the conservative system, then signiﬁcant errors in the corrections 

can

occur because the linear theory assumes small perturbations. In this case, it is preferable to

make the corrections in conﬁguration space rather than velocity space, so long as T

and

remain small.

385 Energy and momentum methods

Proceeding, then, along these lines, we can write

E = T

+ V



= E

(6.445)

where



(q) = V − T

(6.446)

Then, using a similar analysis, and taking the correction q in the direction of the gradient

of V



in conﬁguration space, we obtain

q

=−E





j=1



∂V



∂q





−1

∂V



∂q

(i = 1,...,n) (6.447)

When T

is no longer small, it is preferable to return to corrections in velocity space since

velocity errors tend to be larger.

If the kinetic energy is expressed in terms of quasi-velocities (us) rather than true ve-

locities (

qs), the analysis proceeds similarly to that resulting in (6.443) and (6.444). Thus,

substituting u

for

, we obtain the corrections

u

=−E



n−m



j=1



∂T

∂u





−1

∂T

∂u

(i = 1,...,n − m) (6.448)

where there are m constraints and (n − m) independent us.

Example 6.7 Let us consider the correction of energy errors in the free rotational motion

of a rigid body in space. The rotational kinetic energy is

T =

(6.449)

where the principal moments of inertia are taken about the center of mass. The angular

velocity components (ω

,ω

) are quasi-velocities, so (6.448) applies. The corrections

are

ω

−EI

+ I

(i = x, y, z) (6.450)

Notice that the correction vector ω has the same direction as the angular momentum.

H = I

i + I

j + I

k (6.451)

where (i, j, k) are body-ﬁxed Cartesian unit vectors. This ω is of minimum magnitude

for the given energy correction.

Work and energy

We have been concerned with numerical checks and corrections as they are applied to

conservative systems. Now let us extend the theory to nonconservative systems. We shall

consider two basic methods.

386 Introduction to numerical methods

First method

Let us apply the principle of work and kinetic energy to a system of N rigid bodies. The

velocity of the reference point P

of the i th body is v

and its angular velocity is ω

. The total

effect of all the forces, including constraint forces, which act on the ith body are equivalent

to a force F

acting at the reference point plus a couple of moment M

. Then, since

T =

W (6.452)

where, from (4.357),

W =



i=1

· v

+ M

· ω

) (6.453)

we can integrate with respect to time to obtain

T =





i=1

· v

+ M

· ω

)dt (6.454)

At any time t

, this value of T can be used as a check by comparing it with a value of

T obtained from the solution of the differential equations. To be effective, the separate

integration given by (6.454) must be at least as accurate as the T obtained from the

numerical solution of the equations of motion.

If a portion of F

and of M

arise from a potential energy function V (q, t), but F



and



are the portions that are not due to potential energy, then in accordance with (4.364) we

can write

(T + V ) =







i=1



· v

+ M



· ω

) +

∂V

∂t



dt (6.455)

This calculation can also be used as a check on the numerical solution of differential

equations.

The above approach is relatively direct and effective when it is applicable. It turns out,

however, that F



and M



frequently include unknown constraint forces.

Second method

Another approach is to make energy checks using the energy integral E = T

− T

+ V

rather than the total energy T + V . Consider a nonholonomic system consisting of N rigid

bodies, with a kinetic energy T (q, u, t) and potential energy V (q, t ). Suppose there are n

qs and m constraints. The n

qs and (n − m) us are related by

n−m



j=1



(q, t)u

+ 

(q, t)(i = 1,...,n) (6.456)

387 Energy and momentum methods

The velocity of the center of mass of the ith body is

n−m



j=1

(q, t)u

+ γ

(q, t)(i = 1,...,N ) (6.457)

and the angular velocity is

n−m



j=1

(q, t)u

+ β

(q, t)(i = 1,...,N ) (6.458)

Then, in accordance with (4.380), we ﬁnd that the energy rate is

E =

−

n−m



j=1



∂V

∂t



k=1

∂V

∂q



−



i=1

· ˙γ

−



i=1

(6.459)

where p

is the linear momentum of the i th body and H

is the angular momentum about

its center of mass. Integration of

E with respect to time results in

E =





n−m



j=1



∂V

∂t



k=1

∂V

∂q



−



i=1

· ˙γ

−



i=1



dt (6.460)

This result can be used as a numerical check on the accuracy of E found from the

numerical integration of the equations of motion. For the usual case of ideal constraints

and independent us, the Q



generalized forces will not involve constraint forces, and thus

will be known functions or equal to zero. Note that ˙γ

and

represent linear or angular

accelerations when all the us are set equal to zero, that is, they generally appear only if there

are moving constraints. Thus, in spite of the apparent complexity, (6.460) is often relatively

easy to evaluate.

Example 6.8 Let us consider work and energy relationships for a rheonomic system

consisting of a top whose point is constrained to move uniformly around a horizontal circle

of radius r (Fig. 6.10). The conﬁguration is given by type II Euler angles. Let us choose

(

φ,

θ,)asus, where  is the angular velocity of the top about its symmetry axis. The

angular velocity of the point P along its path is ω

. The ijkunit vectors are as shown,

with i remaining horizontal and jkdeﬁning a vertical plane. Since the motion of the point

P is known, the easiest approach is to consider that point ﬁxed, and then apply a horizontal

inertial force at the center of mass due to the actual acceleration of P. With this assumption,

the velocity of the center of mass is linear and homogeneous in the us, so

= 0 (6.461)

The angular velocity of the top is

θi +

φ sin θ j + k (6.462)

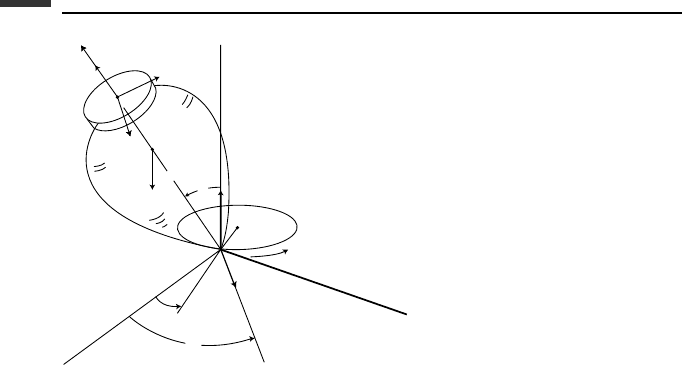
388 Introduction to numerical methods

␾

Ω

Figure 6.10.

Note that

φ = u

θ = u

ψ =−u

cos θ + u

(6.463)

We see from (6.462) and (6.463) that

= sin θ j, β

= i, β

= k, β

= 0 (6.464)

and also that



= 

= 0 (6.465)

The potential energy is

V = mgl cos θ (6.466)

From the general energy rate equation (6.459), we see that the last four terms vanish,

leaving

E =

−

V =



j=1



(6.467)

where the Q



generalized forces are inertial.

The acceleration of P in the actual motion is rω

and is directed from P toward O. The

corresponding inertial force applied at the center of mass results in



= mlrω

sin θ cos(φ − ω



= mlrω

cos θ sin(φ − ω



= 0 (6.468)