Van Kreveld M., Nievergelt J., Roos T., Widmayer P. (eds.) Algorithmic Foundations of Geographic Information Systems
Подождите немного. Документ загружается.

5 = ~ 18 Vl - I,.~ el V2
t2 ~ e2~
20 25 /
t4 t5
t3
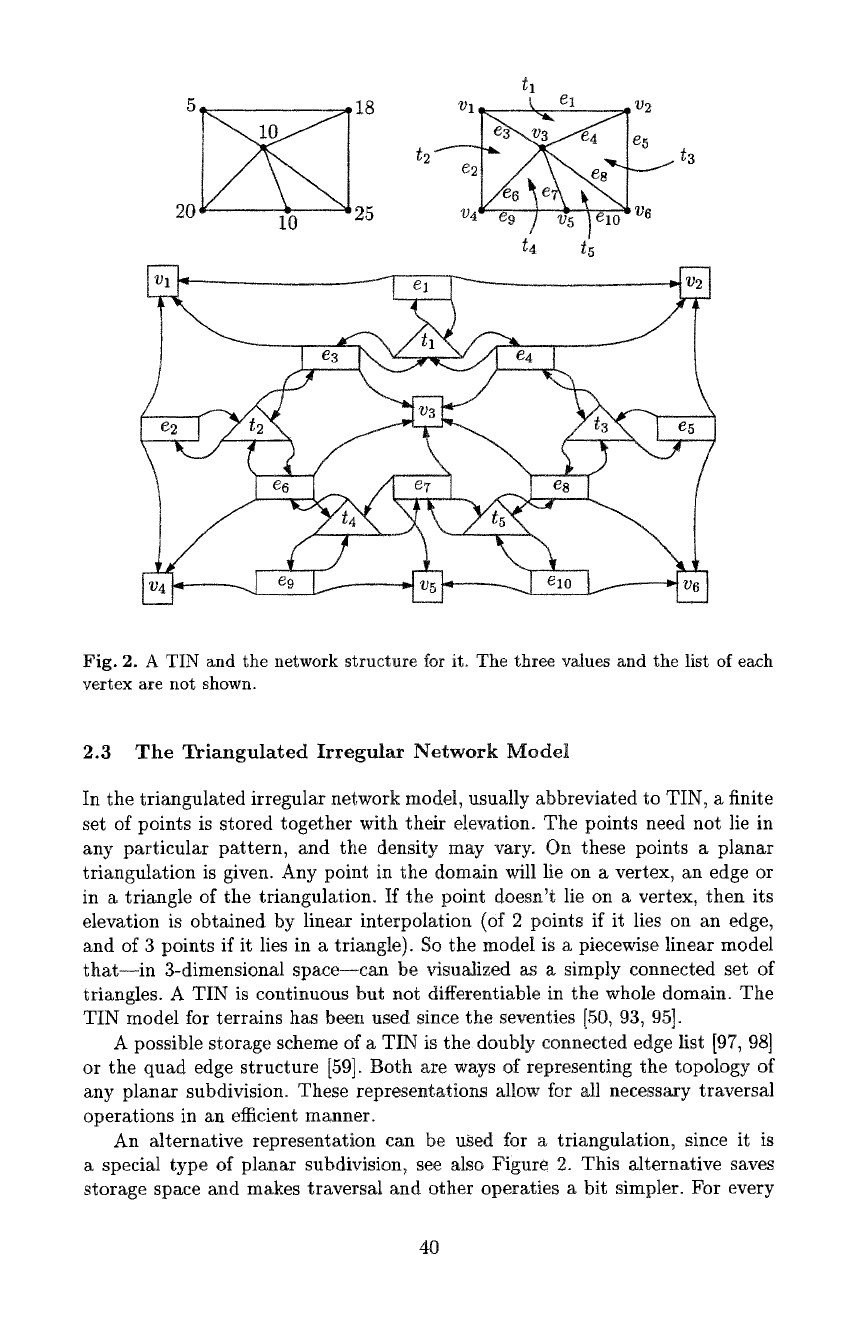
Fig. 2. A TIN and the network structure for it. The three values and the list of each
vertex are not shown.
2.3 The Triangulated Irregular Network Model
In the triangulated irregular network model, usually abbreviated to TIN, a finite
set of points is stored together with their elevation. The points need not lie in
any particular pattern, and the density may vary. On these points a planar
triangulation is given. Any point in the domain will lie on a vertex, an edge or
in a triangle of the triangulation. If the point doesn't lie on a vertex, then its
elevation is obtained by linear interpolation (of 2 points if it lies on an edge,
and of 3 points if it lies in a triangle). So the model is a piecewise linear model
that--in 3-dimensional space--can be visualized as a simply connected set of
triangles. A TIN is continuous but not differentiable in the whole domain. The
TIN model for terrains has been used since the seventies [50, 93, 95].
A possible storage scheme of a TIN is the doubly connected edge list [97, 98]
or the quad edge structure [59]. Both are ways of representing the topology of
any planar subdivision. These representations allow for all necessary traversal
operations in an efficient manner.
An alternative representation can be used for a triangulation, since it is
a special type of planar subdivision~ see also Figure 2. This alternative saves
storage space and makes traversal and other operaties a bit simpler. For every
40

triangle t, edge e, and vertex v, there is a record (or object) for that feature. The
record of a triangle t has three fields with pointers. These pointers are directed
to the records of each of the three edges incident to t. The record of an edge e
has four fields with pointers. Two of the pointers are directed to the records of
the two incident triangles, and the other two pointers are directed to the records
of the incident vertices. The record of a vertex v has three fields with values.
These are the x- and y-coordinates and the elevation of the vertex.
The topological network structure just described allows for finding--for every
triangle--the elevations of its vertices in constant time, finding the adjacent
triangles for a given triangle in constant time, and more. This allows us, for
instance, to walk through the triangulation along a straight line efficiently, which
is necessary to determine a profile of a terrain. Variations on the structure are
possible, for instance by storing a list of pointers at the vertex records to the
incident edges.
2.4 Hierarchical Models
A hierarchical terrain model is a terrain model that represents a terrain in various
levels of error, or, to make it sound less badly, various levels of imprecision.
Most approaches of this type are based on TINs. Generally, TINs with more
vertices have less error than TINs with fewer vertices. On the other hand, TINs
with many vertices are more expensive to compute on. So if it is okay to have
some error in an application, it may be better to work with a TIN with fewer
vertices. A hierarchical terrain model allows the user to choose a terrain with
the appropriate precision for each task.
Issues of importance of hierarchical terrain modelling are:
- The storage required by the model. Explicitly storing a terrain at many levels
of detail leads to redundancy and excessive use of storage.
- The model may incorporate an efficient search structure automatically. For
instance, locating a point on a terrain may be possible by first locating it on
the coarsest level, and then locating it at repeatedly finer levels of detail.
- The triangulations should preferably be well-shaped, for instance, using the
Delaunay triangulation.
- The model may allow a mixture of different detail levels in different parts
of the terrain. This is useful in flight simulation, where the terrain close by
must be shown with more detail than parts far away.
- It may be important that the model is consistent with respect to morphologic
features. For instance, if there is a significant peak in a terrain at some detail
level, one would wish that the same peak also exists on every finer detail level.
The list of issues already indicates that there probably isn't one best solution
to all applications. Many hierarchical terrain models have been suggested [20,
21, 23,38, 65, 103, 121]; the list of references is far from complete. A survey of
the topic also exists [36].
41
3 Access to TINs
3.1 Traversal of a TIN
There is an old but good method to traverse a TIN and visit all its vertices, edges,
and triangles in a simple way [51, 53, 55]. The nice thing about the method is
that hardly any additional storage is needed: no mark bits, no stack, just one
access point to the TIN.
Let T be a TIN stored in the structure just described, and let v be the bottom
left vertex of T. For any triangle, we will give names to the incident edges. This
implies that one edge receives two names, one for each incident triangle. Let t be
//
m ~ ~if in ~ in_and_bac ~
/ t
/ I
$ J I V
V / V i
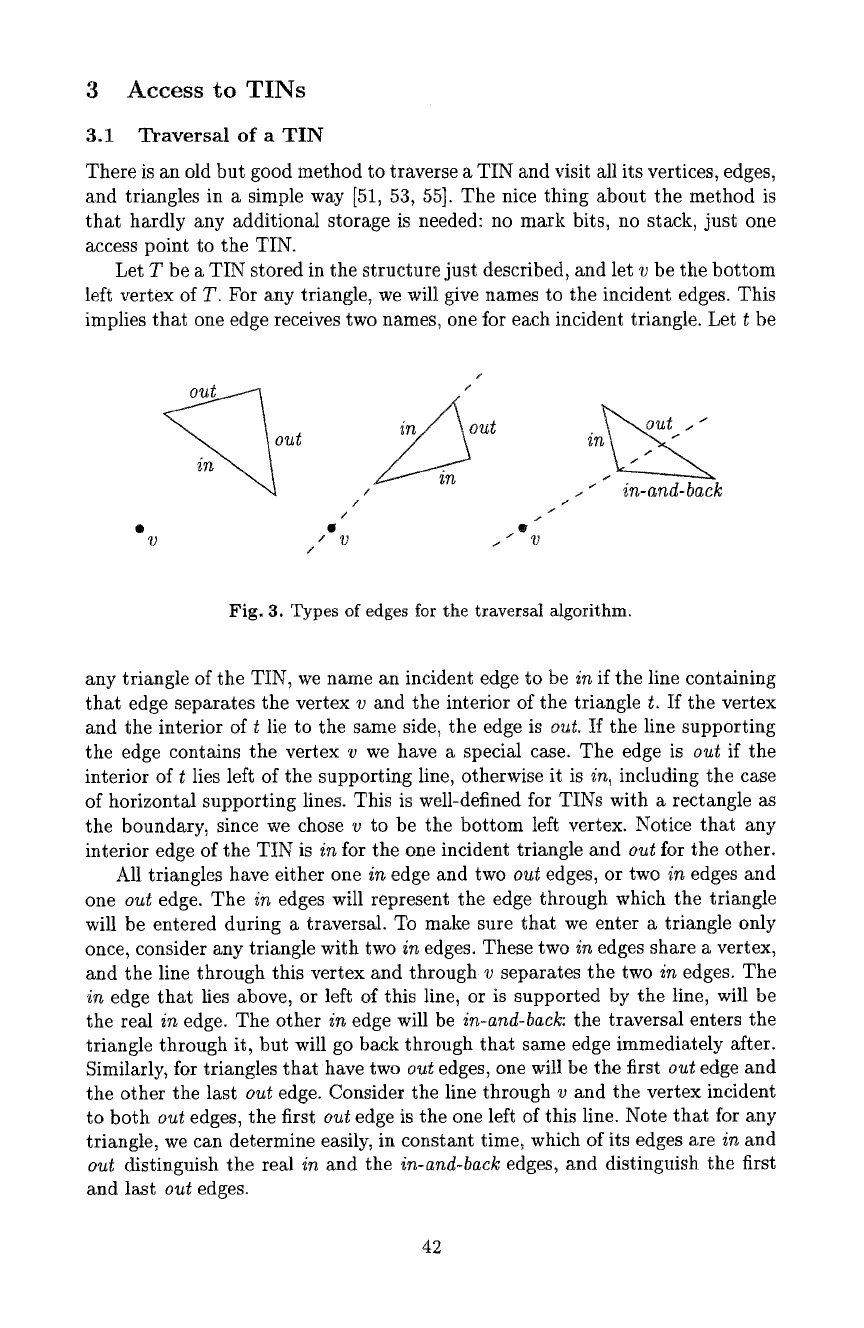
Fig. 3. Types of edges for the traversM algorithm.
any triangle of the TIN, we name an incident edge to be
in
if the line containing
that edge separates the vertex v and the interior of the triangle t. If the vertex
and the interior of t lie to the same side, the edge is
out.
H the line supporting
the edge contains the vertex v we have a special case. The edge is
out
if the
interior of t lies left of the supporting line, otherwise it is
in,
including the case
of horizontal supporting lines. This is well-defined for TINs with a rectangle as
the boundary, since we chose v to be the bottom left vertex. Notice that any
interior edge of the TIN is
in
for the one incident triangle and
out
for the other.
All triangles have either one
in
edge and two
out
edges, or two
in
edges and
one
out
edge. The
in
edges will represent the edge through which the triangle
will be entered during a traversal. To make sure that we enter a triangle only
once, consider any triangle with two
in
edges. These two
in
edges share a vertex,
and the line through this vertex and through v separates the two
in
edges. The
in
edge that lies above, or left of this line, or is supported by the line, will be
the real
in
edge. The other
in
edge wilt be
in-and-back:
the traversal enters the
triangle through it, but will go back through that same edge immediately after.
Similarly, for triangles that have two
out
edges, one will be the first
out
edge and
the other the last
out
edge. Consider the line through v and the vertex incident
to both
out
edges, the first
out
edge is the one left of this line. Note that for any
triangle, we can determine easily, in constant time, which of its edges are
in
and
out
distinguish the real
in
and the
in-and-back
edges, and distinguish the first
and last
out
edges.
42

!'',
/",
,'",
e
?
Fig. 4. Traversing a TIN; numbers at arrows correspond to the algorithm.
The algorithm starts at the triangle that has the bottom left vertex v as a
vertex, and has one edge on the left side of the bounding rectangle. Let that
triangle be t, and let e be the edge on the left side. The algorithm proceeds from
triangle to triangle by crossing edges, and make the decision on which edge to
cross next based solely on the type of edge through which it was just entered,
and the type of triangle it is currently in. Since there are two types of triangles,
and each has three edges, the algorithm distinguishes six cases to decide how the
traversal should proceed, see also Figure 4. Edge e will be the first edge crossed
in the traversal. When the algorithm reaches e a second time, the traversal is
completed.
1. If e is the only
in
edge of t~ then let e r be the first
out
edge of t, and let t t
be the triangle on the other side of e. Repeat the algorithm with t := t v and
e :~ et.
2. If e is the real
in
edge of t, then let e r be the
out
edge of
t,
and let t I be
the triangle on the other side of e 1. Repeat the algorithm with t := t / and
e :~-- e I.
3. If e is an
in-and-back
edge of t, then let t I be the triangle on the other side
of e. Repeat the algorithm with t := t I and e.
4. If t has two
out
edges and e is the first one, then let e t be the last
out
edge
of t, and let t r be the triangle on the other side of it. Repeat the algorithm
with t := t ~ and e := e r.
5. If t has two
out
edges and e is the last one, then let e ~ be the
in
edge of t,
and let t t be the triangle on the other side of it. Repeat the algorithm with
t := t t and e := e t.
6. If e is the only
out
edge of t, then let e' be the real
in
edge and t ~ the triangle
on the other side of it. Repeat the algorithm with t := t I and e := e ~.
If there appears to be no triangle on the other side of the edge we have just
crossed, then we return to the previous triangle through the same edge we just
43

left immediately. Then we proceed as usual: the current triangle has just been
entered through an edge that happens to be part of the bounding rectangle.
The algorithm visits every triangle exactly three times, once through each of
its edges. At all times, we need only know the current triangle, the edge through
which it was accessed, and the vertex v. We can report a triangle when we visit
it for the first time. If all edges or all vertices of the TIN should be reported,
some simple adaptations are needed.
The idea described above has been extended to the traversal of other subdi-
visions than just triangulations [19, 26].
3.2 Efficient Access to a TIN
In a regular square grid structure there is direct access to every part of the
terrain. If one wants to know the elevation at a point with coordinates x and y,
these coordinates can simply be rewritten to index values in the two-dimensional
array, tn a TIN this is not so easy, because a TIN is a pointer structure. If one
wants to know the elevation at a point given its coordinates, one could test each
triangle to see if it contains the point. This is rather inefficient, obviously. We
briefly review three methods to gain access to the TIN at a specific point.
Access using quadtrees. Quadtrees and other spatial indexing structures like
R-trees can be used to get access to a TIN at a specific query point efficiently.
A quadtree is a rooted search tree of degree four, meant to store 2-dimensional
data. Its nodes represent a recursive decomposition of a big square (associated
with the root of the quadtree) into four subsquares (the children of the root).
Each of the four subsquares is decomposed into four yet smaller squares. Further
decomposition stops as soon as the part of the TIN that falls in the subsquare is
simple enough. For example, when only a few vertices of the TIN lie inside the
square. A leM node is created that represents this square, and at the leaf node
we store a pointer to the triangle record of the triangle that contains the center
of the square. From that triangle record we can walk in the topological structure
to locate the triangle record of the triangle that contains the query point.
Another possibility is to take the smallest enclosing axis-parallel rectangle
of each triangle of the TIN. The resulting set of rectangles may overlap, but
one can expect that at each point there won't be many rectangles containing
it. A quadtree, R-tree, or other 2-dimensional search tree can be used to store
the rectangles, see for instance the book by Samet [100]. For a query point, we
determine all rectangles that contain it, and then find the triangle enclosed by
one of the located rectangles that really contains the query point.
Access using planar point location. In the computational geometry field
several efficient methods have been developed to determine which region of a
subdivision contains a given query point. This problem is known as point loca-
tion. For a TIN with n triangles, it is possible to construct an
O(n)
size data
44

structure that allows for point location in O(logn) time. Among the many re-
sults, the most simple and efficient ones are by Sarnak and Tarjan [101], Clarkson
and Shot [12], Kirkpatrick [66] and Seidel [105]. Descriptions can also be found
in textbooks on computational geometry [18, 91, 98].
Jump-and-walk strategy. The simplest method to locate a point in a TIN
among these three is the jump-and-wMk strategy. It also requires very little
additional storage, so it may well be the best choice in practice. Suppose that
access to the TIN structure is provided by one pointer to some feature. Rather
than traversing all triangles until we find one that contains the query point, we
can also traverse the TIN in a straight line from the access point to the query
point. We typically encounter much fewer triangles on the way than if we would
traverse the whole structure. The query time will be even better to take more
than one starting point. Among those we'll choose as the real starting point the
one closest to the query point, in the Euclidean sense.
Fig. 5. Jump-and-walk with three starting points.
There are two natural schemes for choosing starting points. They can be
placed in a regular, grid-like pattern, and stored in a 2-dimensional array with a
pointer from each entry into the TIN structure. The pointer gives access to the
triangle record that contains the point of the regular grid. This first scheme is
good in most practical situations. If there are parts of the TIN" where many small
triangles occur, then the scheme is not so good. Either we don't have fast access
to region with small triangles, since we must walk through many triangles before
reaching the point to be located, or we must store a large array. A second scheme
that overcomes this problem is the following. Choose m points PI,--. ,P,~ from
the set of vertices of the TIN at random, and store a copy of those points in an
unsorted list. By choosing the points from the TIN vertices, we generally have
that regions that contain many triangles will also have several access points.
With each point Pi we store a pointer to one of the triangle records incident to
the point. When we query with a point q, we first determine the access point
45

p~ closest to q in
O(m)
time, and then we start tracing the line segment ~-q,
starting at the triangle containing pi. It appears that the choice
m = c. n 1/3
for
a constant c is good. There is also some theoretical justification for this [3, 88].
3.3 Windowing
When a user is interested in a part of a terrain, then this part must be extracted
from the whole terrain. We assume that the selection of the interesting part
is defined by some rectangle, the window, and all triangles intersecting that
rectangle should be located. Again we take the TIN as the elevation model to
which windowing is applied.
The algorithm consists of two steps. First, the position of the window on the
terrain should be located, and second, the TIN triangles inside the window can
be traversed. We can locate for instance the upper left corner of the window, and
start traversing from there; we already discussed ways to locate a point in a TIN.
Traversal can be done in time linear in the number of triangles intersecting the
window. The ideas of traversal without mark bits can also be applied here [19].
4 Conversion between Terrain Models
Terrain data can be entered into a GIS in various formats. Often, contour line
data is entered when paper maps with contour lines are digitized by hand. Also
quite often, gridded data is the input format, for instance when the data is
acquired by remote sensing or automatic photo-interpretation. There are vari-
ous reasons why data in one format may need to be transformed into another.
Gridded data usually is huge in size, resulting in high memory requirements
and slow algorithms when the data is processed further. Contour line data often
needs to be interpreted anyway before anything useful can be done with it. In
several cases it may help to store and compute with TINs instead. Conversion
from TINs into grids or contour lines may also be useful. The former problem
is algorithmically quite straightforward and we won't discuss it here. The latter
problem shows up when a TIN is visualized as a contour map; we deal with that
issue later in Section 6.
This section gives a few algorithms and references for converting to TINs.
First we discuss how point sample data can be converted to a TIN, then grid-
to-TIN conversion is handled, and then we go from contour lines to a TIN.
4.1 From Point Sample to TIN
Suppose a set P of n points in the plane is given, each with an elevation value.
To convert this information into a TIN, one could simply triangulate the point
set. In fact, the triangulation is an interpolation of a region based on the points
of P. It is common to use the Delaunay triangulation because it attempts to
create well-shaped triangles. Efficient algorithms for the Delaunay triangulation
46

have been known for a while. See for instance Lee and Schachter [74], Guibas
and Stolfi [59], or any textbook on computational geometry [18, 91, 98].
When the interpolation provided by the Delaunay triangulation is not appro-
priate, one can use different, more advanced interpolation methods like natural
neighbor interpolation [54, 99, 106], weighted moving averages [4], splines [40],
or Kriging [4, 123]. It is possible to combine the advantages of the TIN with the
quality of these more advanced interpolation methods as follows. Suppose we are
given the point set P together with an interpolation function and a maximum
error. The idea is: construct a TIN based on P and the interpolation function,
such that at any point, the interpolated elevation and the elevation given by the
TIN differ by at most the maximum error. Now it may not suffice to use only
the points of P as TIN vertices, and we need to select more points. Ideally, we
select as few points as possible, the optimization problem that shows up is very
difficult. Heuristics can be used to choose additional points as vertices in the
TIN, and hopefully not too many additional ones. It may also be the case that
only a subset of the points of P is needed to represent the interpolation function
with the desired accuracy. Or perhaps a completely different set of points is best.
In any case, finding a TIN with minimum number of vertices will be difficult.
It is known that the problem of computing a TIN with the minimum number
of vertices, given a TIN and a maximum allowed error, is an NP-hard problem,
implying that efficient algorithms are unlikely to exist.
4.2 From Grid to TIN
Grid-to-TIN conversion can be seen as a special case of the conversion of sample
points to a TIN. Also, grid-to-TIN conversion can be seen as a special case
of TIN generalization: reducing the number of vertices of a TIN to represent
a terrain. A grid can simply be triangulated to a fine regular triangulation.
Various algorithms have been proposed in the literature; see for instance the
survey by Garland and Heckbert [49], see also Lee [78]. Most of the methods
have the following distinguishing features: (1) selecting which grid points to
keep or discard, and (2) deciding when to stop selecting or discarding.
One method decides which grid points to keep or discard by initially assigning
an importance to each grid point [8]. The importance is determined by comparing
the elevation of a grid point with the interpolated elevation at the grid point
based oll the elevations of the eight neighbors. Only the grid points where the
difference is greatest are kept. These points can be triangulated, for instance
using the Delaunay triangulation, and become the TIN vertices.
A second method differs from the previous one by discarding grid points
incrementally instead of using a precomputed importance [77, 78]. In a sense,
the importance computation is postponed until the point is really discarded. A
more detailed description follows later.
Thirdly, there are methods that start out with a coarse triangulation of only
the four corner grid prints, and keep on refining the triangulation by adding
more points in the triangles [34~ 49, 61, 108]. Refining a triangle further stops
when the triangle approximates the grid points that lie in it sufficiently well.
47

\/
Fig. 6. Left, a TIN with one vertex indicated by a circle. Middle, the polygon that
appears when the indicated vertex is removed. Right, a Delaunay triangulation of the
polygon.
Another method start out by detecting surface specific features on the grid
like peaks, pits, saddle points, ridges, and valley lines [41]. Then they complete
these retained points and line segments to a TIN. Extraction of surface specific
features is discussed later in this survey.
We describe two methods in more detail, namely, the drop heuristic method
by Lee [77, 78] of the second type, and a method by Heller [61] (see also
Fj£11strSm [34] and Garland and Heckbert [49]) of the third type.
The drop heuristic. Lee's drop heuristic method takes a TIN as its input,
and iteratively discards one vertex at a time to obtain a TIN with fewer vertices.
Obviously, it also applies to grids as input if we consider it to be a triangulated
regular grid. If a vertex is discarded, the incident edges are also removed and a
polygon appears in the subdivision. To get back to a triangulation, the polygon
is triangulated using the Delaunay triangulation. This will ascertain that if the
algorithm starts with a Detaunay triangulation, then after every iteration we'll
still have a Delaunay triangulation.
To decide which vertex should be discarded, each vertex is temporarily re-
moved and the appearing polygon is triangulated--see Figure 6. Then we deter-
mine the vertical distance between the removed point and the new, simplified
TIN. The removed vertex lies in one of the new triangles in the polygon, so
this is easy to do. This vertical distance can be viewed as the error introduced
by the deletion. Once we know the error that would be introduced, we add the
removed vertex back to the TIN and temporarily remove another vertex. After
we have done so for M1 vertices, we select the one for which the computed error
is smallest and really discard it. The process continues until the created error is
more than the prespecified allowed error.
It should be noted that the error at a vertex after it is discarded can become
bigger when more vertices are discarded. So there is no guarantee that the error
at M1 of the discarded vertices really is within the prespecified error. The drop
heuristic method completely forgets about vertices that are discarded, a~though,
48

at the expense of more computation, a variant of the method could still consider
them. Below we'll analyze the typical running time of the standard algorithm.
A straightforward implementation of the algorithm requires
O(n
log n) time
per iteration on a TIN with n vertices. Discarding the vertices temporarily to
determine their error and retriangulation can be done in
O(n
log n) time in total.
This is true because the total complexity of all polygons to be triangulated is
linear in n. Unfortunately, the vertical distances may have to be recomputed
after an iteration, because the deletion of some vertex may result in a change
of introduced error of other vertices. It is possible to construct an example of
a TIN with n vertices where the algorithm has to recompute the errors many
times for many vertices, but this is not a typical case. Observe that if a vertex v
is removed in some iteration, then only the vertices of the TIN adjacent to v can
have a change in introduced error. For all other vertices, the error resulting from
their removal stays the same. So the question is how many neighbors a vertex in
the Delaunay triangulation has. In the worst case this number may be n - 1, all
other vertices, but on the average, a vertex has degree at most six. We'll analyze
the typical case where any vertex that is removed has constant degree. Under
this assumption we can design a variation of the given algorithm that will run
in
O(n
log n) time. We describe this variation below.
1. For each vertex v in the TIN:
- Temporarily remove it v.
-
Compute the Delaunav triangulation of the appearing polygon.
- Determine the vertical distance
error(v)
of v to the new TIN.
- Add the removed vertex back to the TIN.
Store
error(v)
for each vertex v sorted in a balanced binary tree T. At each
node of T storing some
error(v),
store a pointer to the vertex v in the TIN.
At v, we store a pointer back to the corresponding node in 7".
2. Consider the node with smallest
error(v)
in 7". If it is greater than the
prespecified maximum error~ the algorithm stops. Otherwise it proceeds with
the next step.
3. Remove the node storing the smallest
error(v)
from 7". Remove the corre-
sponding vertex v from the TIN structure. Let Wl,...,wj be the vertices
adjacent to v. Retriangulate the polygon defined by Wl,...
,wj
using the
Delaunay triangulation.
4. For every vertex w~ E {wl,... ,wj}:
- Remove the node that stores
error(w~)
from 7-.
-
Recompute the vertical distance to the terrain if wi were removed as we
did in the first step.
- Insert the new
error(w~)
in 7".
Continue at step 2.
If all vertices in the TIN have constant degree, then each iteration requires
only O(log n) time. The polygon to be retriangulated only has a constant num-
ber of vertices, and only for these a new vertical distance need be computed.
The insert and delete operations on the tree T take O(log n) time each. So the
algorithm takes only
O(n
log n) time in typical cases.
49
