Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

B.2 ERROR IN N UMERICAL I NTEGRATION

n+1

(a) (b)

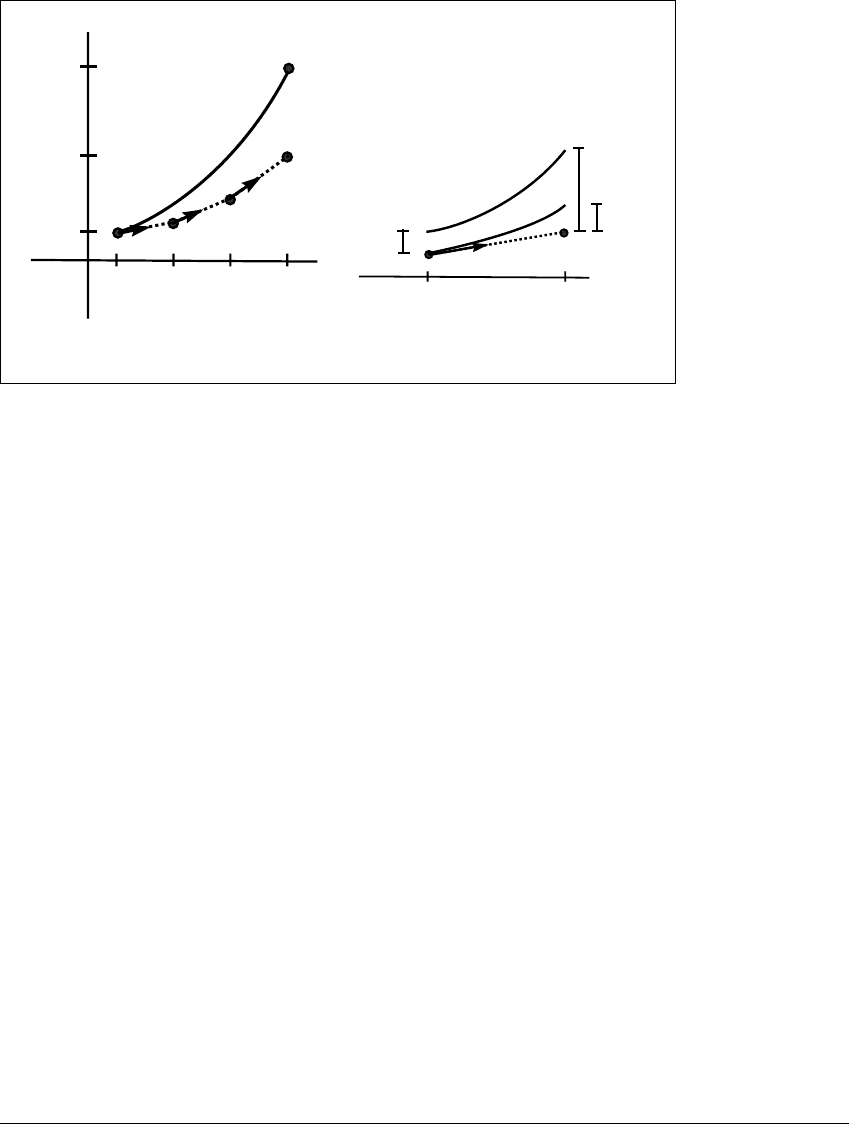
Figure B.1 Output from an ODE solver.

(a) The Euler method follows a line segment with the slope of the vector ﬁeld at

the current point to the next point. The upper curve represents the true solution to

the differential equation. (b) The total error E

n⫹1

is the total of the one-step error

n⫹1

and accumulated error from previous steps.

After one step, the total error E

is the same as the one-step error e

.The

total error E

after two steps has two contributions. First, because of the error E

the right side f of the differential equation is going to be sampled at an incorrect

point w

instead of x

. Second, a new one-step error e

will be made because of

the discretization of the derivative. As Figure B.1(b) shows, the new total error

will have a contribution from the accumulated error from the previous step as

well as a new one-step error.

The output of the Euler method is w

⫽ x

(1 ⫹ ah)

for n ⱖ 0. The true

solution is x

⫽ x

ahn

, so that the difference is

⫽ x

⫺ w

⫽ x

ahn

⫺ x

(1 ⫹ ah)

⫽ x

ahn

⫺ x

(1 ⫹ ah)

n⫺1

⫹ x

(1 ⫹ ah)

n⫺1

⫺ x

(1 ⫹ ah)

⫽ e

⭈ x

ah(n⫺1)

⫺ (1 ⫹ ah)

n⫺1

) ⫹ w

n⫺1

⫺ (1 ⫹ ah)). (B.6)

We recognize E

n⫺1

, the total error at step n ⫺ 1, and e

, the one-step error at

step n , in the above equation. If we set A ⫽ e

, we can write the result in the

following general form.

571

C OMPUTER S OLUTION OF ODES

TOTAL E RROR FOR AN ODE SOLVER

⫽ AE

n⫺1

⫹ e

In this expression, the term A is the ampliﬁcation factor. It depends on the

method being used and the particular differential equation. If A ⬇ 1, one expects

the total error to be approximately the sum of the one-step errors. For IVPs that

are sensitive to initial conditions, however, the ampliﬁcation factor is commonly

greater than one. For system (B.1), this case holds when a ⬎ 0.

The order of an ODE solver is a measure of its relative accuracy. Let t

the initial time of the IVP, and let t

⬎ t

be a later time. By deﬁnition, the order

of an ODE solver is k if the total error evaluated at t

E ⬇ Ch

(B.7)

for small h. More precisely, one requires

lim

h→0

⬍

⬁

Order measures the dependence of the total error on the stepsize h, and is helpful

in a relative way. It gives no absolute estimate of the error, but it tells us that the

error of a second-order method, for example, would decrease by a factor of 4 if we

cut the step size in half (replace h by h 2 in (B.7)). This concept of order is used

to rank methods by accuracy.

The order of an ODE solver can be informally determined by expressing

the one-step error in terms of h. Using the differential equation (B.3), the Taylor

expansion of the solution at t

can be written

x(t

⫹ h) ⫽ x

⫹ h

x(t

) ⫹

x(t

) ⫹⭈⭈⭈

⫽ x

⫹ hf(t

) ⫹



⳵

) ⫹

⳵



⫹⭈⭈⭈. (B.8)

Comparing with the Euler’s method approximation (B.4), we ﬁnd the one-step

error e

to be proportional to h

, where terms of higher degree in h are neglected

for small h. To ﬁnd the order of the method, subtract one from the power of h in

the one-step error. The reasoning is as follows. Assuming that the ampliﬁcation

factor is approximately one, the simplest case, the total error made by the ODE-

solver between t

and t

will be approximately the sum of the one-step errors.

572

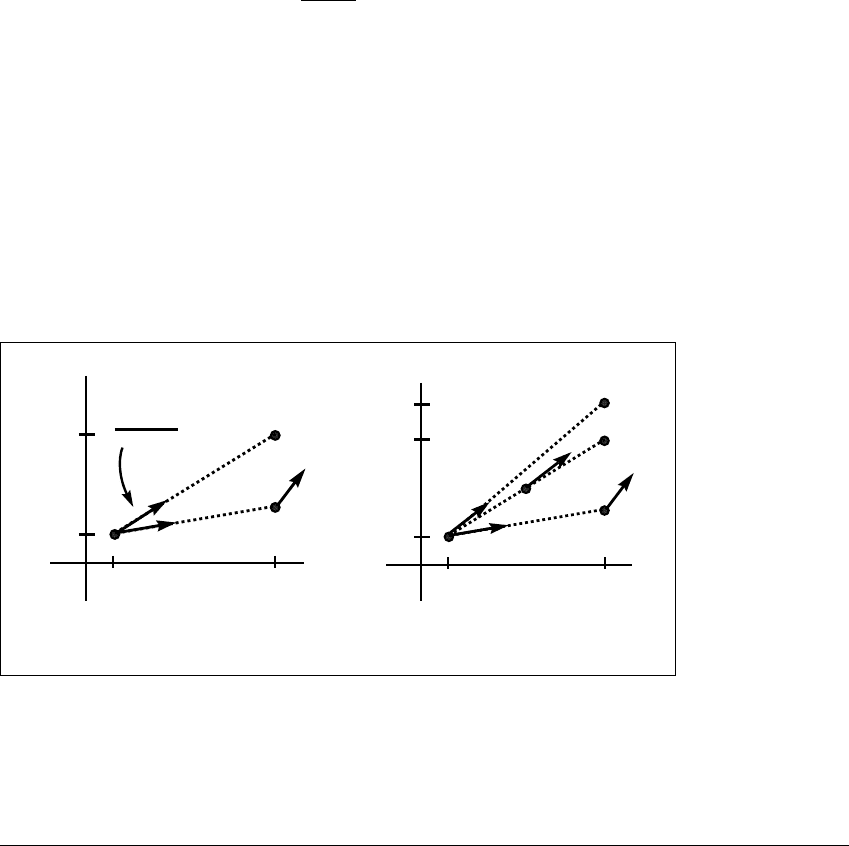
B.2 ERROR IN N UMERICAL I NTEGRATION

The number of steps needed to reach the desired time t

grows as h decreases: It

is proportional to h

⫺1

. The total error for the Euler method, as a function of h,

should therefore be proportional to h

⭈ h

⫺1

⫽ h

. On this basis, the Euler method

is of order one. Cutting the step size in half results in cutting the total error in

half.

Higher order methods can be derived by more elaborate versions of the

reasoning used in the Euler method. The modiﬁed-Euler method is

⫽ x

n⫹1

⫽ z

⫹ h

⫹ s

for n ⱖ 1, (B.9)

where s

⫽ f(t

)ands

⫽ f(t

⫹ h, z

⫹ hs

). It can be checked that the one-

step error for this method is ⬇ h

(see, for example, (Burden and Faires, 1993)).

Figure B.2(a) shows one step of the method along with the roles of s

,whichis

the slope of f as in the Euler method, and s

, which is the slope at t

n⫹1

,wherethe

Euler method is used as a guess for x

n⫹1

. Instead of taking the Euler method step,

the two slopes s

and s

are averaged, and a step is taken with the averaged slope.

This is a simple predictor-corrector method, in which the Euler method is used

to predict the new solution value, followed by a more accurate correction. Note

that the correction cannot be made without knowing the prediction.

n+1

+ s

n+1

(a) (b)

Figure B.2 The geometry of a higher-order one-step method.

(a) The Modiﬁed Euler method takes an Euler step whose slope is the average of

the two slopes shown. (b) A third-order method ﬁrst uses modiﬁed Euler to ﬁnd the

vector ﬁeld in the middle of the time interval, and translates the slope s

determined

there back to t

. Then an Euler step is taken with slope s

to produce (t

n⫹1

573

C OMPUTER S OLUTION OF ODES

B.3 ADAPTIVE STEP-SIZE METHODS

Thus far we have treated the step size h as a constant throughout the calculation.

We have given no advice on how to choose h, except to say that the smaller the

h, the smaller the error. Adaptive methods ﬁnd the best step size automatically,

and constantly recalculate the optimal size as the calculation proceeds.

Matlab’s ode23 program is an adaptive method using second-order modi-

ﬁed Euler along with the third-order method

⫽ x

n⫹1

⫽ w

⫹ h

⫹ 4s

⫹ s

for n ⱖ 1, (B.10)

where s

and s

are as deﬁned for the modiﬁed Euler method and s

⫽ f(t

⫹

h 2,w

⫹ (h 2)(s

⫹ s

) 2). As sketched in Figure B.2(b), the average slope

used to calculate z

n⫹1

in the Euler-type step in the modiﬁed Euler method is used

instead to sample the differential equation for a new slope at t

⫹ h 2. This slope

is used for the Euler-type step from t

to t

n⫹1

To get the program to adjust the step size h automatically, the user must set

a tolerance TOL for the one-step error. For the new step, both the second-order

approximation z

n⫹1

from (B.9) and the third-order approximation w

n⫹1

from

(B.10) are calculated. Since the third-order approximation is so much better, the

difference between the two is a good approximation for the one-step error of z

n⫹1

that is, e(h) ⬇ |z

n⫹1

⫺ w

n⫹1

|. Denote by c the factor by which we want to change

the step size. Then the new step size should be the ch that satisﬁes TOL ⫽ e(ch),

which can be approximated as follows:

TOL ⫽ e(ch) ⬇ c

e(h) ⬇ c

n⫹1

⫺ w

n⫹1

|. (B.11)

Here we have used the fact that the one-step error of the (second-order) modiﬁed

Euler method is proportional to h

. Now (B.11) can be solved for c:

c ⫽



TOL

n⫹1

⫺ w

n⫹1



1 3

. (B.12)

Two further points make the automatic choice of step size conservative. First, the

new h is set to be 0.9ch instead of ch. Second, although the step size is being set

to keep one-step error within the preset tolerance for the second-order method,

the third-order approximation w

n⫹1

is accepted as the new value of the solution.

Matlab also provides a higher-order adaptive method called ode45.This

is an implementation of the Runge-Kutta-Fehlberg method. It uses a variation

574

B.3 ADAPTIVE S TEP-SIZE M ETHODS

of the fourth-order Runge-Kutta method described above together with a ﬁfth-

order method that can be accomplished while reusing some of the fourth-order

calculations, in the same spirit as ode23. This method, often denoted RK45 in

other sources, is very popular for applications in which running time is not a

critical factor.

Depending on your intended use, we have either completely solved the

problem of computational solution of differential equations, or have barely

scratched the surface. One-step methods are ﬁne for the simulations we have

outlined in this book, but are too slow for industrial-strength applications. A

rough way to compare the computational effort required for ODE methods is to

count the number of times per step that f, the right-hand side of the equation,

needs to be evaluated.

As we saw in the above code fragment, fourth-order Runge-Kutta requires

four function evaluations per step, for a one-dimensional system. It is not hard

to derive multistep methods that are fourth order but require only one function

evaluation per step. A multi-step ODE method uses not only the previous esti-

mate w

, but several previous estimates w

n⫺1

,... to produce w

n⫹1

. In fact,

it is fairly wasteful of one-step methods to ignore this available information. If

most of the computational effort lies in the evaluation of f, we would expect a

fourth-order multistep method to run four times as fast as RK4.

Multistep methods have some liabilities. The most obvious is that starting

the method is nontrivial. Usually, a one-step method is used to intialize the pre-

vious w

estimates that are needed. Second, when adaptive step sizing is used, the

fact that the previous estimates w

n⫺1

,...are not equally spaced complicates

the formulas signiﬁcantly. A new generation of methods called multivalue ODE

methods has recently been introduced to alleviate some of these problems. We

refer you to a current numerical analysis textbook, such as (Burden and Faires,

1993) to read more about these issues.

575

Answers and Hints to

Selected Exercises

T1.2 Hint: Mimic the proof of Part 1.

T1.3 The points in the open intervals (⫺1, 0) and (0, 1) satisfy |f(x)| ⬎ |x|,and

converge to sinks ⫺1 and 1, respectively. The points |x| ⬎



5 satisfy |f(x)| ⬎ |x|,

and because they increase the distance from the origin on each iteration they

cannot converge to either of the sinks.

T1.4 One condition is that f lies strictly between the lines y ⫽ p and y ⫽ x in (p ⫺

⑀

p ⫹

⑀

T1.5 兵1 ⫹



2, 1 ⫺



2其.

T1.7 兵(5 ⫹



5) 8, (5 ⫺



5) 8其.

T1.8 f

has 2

ﬁxed points. Some are also ﬁxed points of period less than k, but since

⫺ (2

k⫺1

⫹ 2

k⫺2

⫹ ...⫹ 2

) ⫽ 2, not all can have period less than k.

577

A NSWERS AND H INTS TO S ELECTED E XERCISES

T1.10 If x is eventually periodic, then 3

x ⫽ 3

x (mod 1). Since (3

⫺ 3

)x is an integer

p, x ⫽ p (3

⫺ 3

) is a rational number. Conversely, assume x ⫽ p q,wherep

and q are integers. The integers 3

p cannot all be distinct modulo q, since there

are only q possibilities. For some integers m and n,3

p ⫽ 3

p (mod q), which

implies 3

p q ⫽ 3

p q (mod 1).

T1.14 (a) Any number between (2 ⫺

2 ⫹



2) 4and(2⫺



2) 4 will do.

T1.16 (a) Greater than 1 2 (b) Less than 1 2.

1.1 l has an attracting ﬁxed point if and only if ⫺1 ⬍ a ⬍ 1, and has a repelling

ﬁxed point if and only if a ⬍⫺1ora ⬎ 1. There is a ﬁxed point that is neither

attracting nor repelling if a ⫽⫺1, and many such if a ⫽ 1andb ⫽ 0. If a ⫽ 1

and b ⫽ 0, the map l has no ﬁxed point.

1.3 x ⫽ 0 is a source.

1.5 Source.

1.9 (a)



2. (b) ⫺



2 and all preimages of ⫺1. Hints: Draw the graph and show that

except for the undeﬁned orbit with x

⫽⫺1, all orbits that ever reach outside

[⫺1.5, ⫺1.4] converge to



2. Note that the endpoints of this interval both map

to ⫺1, so the remainder of the orbit (and limit) is undeﬁned. Next show that

any point inside this interval is repelled from ⫺



2 at the rate of more than a

factor of 4 per iterate, so that no orbit other than the ﬁxed orbit 兵⫺



2其 can

avoid eventually leaving the interval. Most leave the interval and converge to



2; a few unlucky ones land on ⫺1.5or⫺1.4 on the way out and end up with

undeﬁned orbits.

1.11 (b) Hint: Show that (f

)



(x) ⱖ 0forallx.

1.15 The only ﬁxed point is x ⫽ 0. Orbits with initial conditions in [⫺1, 0] are

attracted to 0; all other orbits diverge.

1.16 Hint: Check for n ⫽ 0. To prove the formula for n ⫽ 1, you may need the

double-angle formula: cos 2x ⫽ 1 ⫺ 2sin

T2.4 Hint: Write the vector in polar coordinates and use the sin and cos addition laws.

T2.7 (b) ⫺1. (d) ⫺1.

T2.8 The inverse map is g(x, y) ⫽ (y, (x ⫺ a ⫹ y

) b). If b ⫽ 0, then the points (1, 0)

and (1, 1) map to the same point, so the map is not one-to-one.

T2.9 (b) Part (a) conﬁrms that the orbit of any point on S stays on S, a parabola through

0. Since the x-coordinate of the orbit is halved each iteration, it converges to 0,

and the y coordinate must follow.

T2.10 The axes of AN are of length 4 3and1 3 along the directions (2, 1) and (1, ⫺2),

respectively.

578

A NSWERS AND H INTS TO S ELECTED E XERCISES

2.1 (a) Source (b) Saddle (c) Sink.

2.2 (0, 0).

2.3 (0, 0) is a saddle and (3, 9) is a source.

2.4 (a) (⫺0. 7, ⫺0.7) is a ﬁxed sink, (⫺0.8, ⫺0.8) is a ﬁxed saddle; there are no

period-two orbits. (b) (⫺0.7, ⫺0.7) and (0.3, 0.3) are saddles and 兵(0.5, ⫺0.1),

(⫺0.1, 0.5)其 is a period-two sink orbit.

2.7 (a) ⫺0.1225 ⬍ a ⬍ 0.3675 (b) 0.3675 ⬍ a ⬍ 0.9125

2.8 (a) Image ellipse has one axis of length 2



2inthedirection(1, 1), and another

of length 1



2inthe(⫺1, 1) direction. Area is 2

␲

. (b) Ellipse has axes of

length 3 and 2, and area of 6

␲

T3.2 Hint: Find the Lyapunov exponents of all ﬁxed points, and then show that all

orbits either are unbounded or converge to one of the ﬁxed points.

T3.3 If f has a period-n orbit, then f

) ⫽ x

⫹ nq ⫽ x

(mod 1), so that nq is an

integer. That is not possible since q is irrational. The Lyapunov exponent of the

orbit of any x

is lim

n→

⬁

[ln 1 ⫹ ...⫹ ln 1] ⫽ 0.

T3.4 The set of points which share the same length-k itinerary is a single subinterval

of length 2

⫺k

. An inﬁnite itinerary corresponds to the nested intersection of

subintervals of length 2

⫺k

,kⱖ 1, which is a single point.

T3.7 First check that T

(x) ⫽ x if and only if G

C(x) ⫽ C(x), for any positive integer

n.Ifx is a period-k point for T,thenT

(x) ⫽ x implies G

C(x) ⫽ C(x). The

equality G

C(x) ⫽ C(x) cannot hold for any n ⬍ k because it would imply

(x) ⫽ x, which is not true—x is a period-k point. Therefore C(x)isaperiod-k

point for G.

T3.8 The ﬁrst statement of Theorem 3.11 is Exercise T3.7. Secondly, apply the

chain rule to the equation g

(C(x)) ⫽ C(f

(x)) to get (g

)



(C(x))C



(x) ⫽



(x))(f

)



(x). Since f

(x) ⫽ x and C



(x) ⫽ 0, cancelling yields (g

)



(C(x)) ⫽

)



(x).

T3.10 (a) The itinerary LRR ⭈⭈⭈R, consisting of one L and k ⫺ 1R’s, is not periodic for

any period less than k. (b) According to Corollary 3.18, the interval LRR ⭈⭈⭈RL

contains a ﬁxed point of f

. By part (a), that point must be part of a period-k

orbit.

T3.12 The twelve distinct periodic orbits of period ⱕ 5are:

L, KL, JKL, KLL, JKLL, KLLL,

IJKL, JKLLL, KLLLL, KLJKL, KLKLL,andIJKLL.

3.1 (a) a

⫽⫺1 4. (b) ⫺

⬁

.(c)a

⫽ 3 4. (d) a

⫽ 5 4. (e) First ﬁnd an interval

which maps onto itself. Then ﬁnd a partition as was done for the logistic map G.

579

A NSWERS AND H INTS TO S ELECTED E XERCISES

3.3 (a) G maps [0, 1] onto itself and g maps another interval onto itself. C will be a

one-to-one continuous map between [0, 1] and the other domain interval.

3.4 Hint: See Exercise T3.2.

3.5 (b) [1, 2] and [2, 3]. (c) The transition graph is the fully connected graph on two

symbols. There exists periodic points of all periods.

3.8 (a) All positive integers except 3, 5, and 7. (b) All positive integers.

3.9 (c) All positive integers.

3.10 All positive integers except for 3.

3.11 (b) Hint: Explain why either f or f

must have points 0 ⱕ x

⬍ x

ⱕ 1suchthat

maps to 0 and x

maps to 1.

3.12 Hint: Find a positive lower bound for f



on [0, 1].

T4.2 The expansions end in 0

T4.7 Complete the square by replacing w ⫽ x ⫺ 1 2.

T4.8 Hint: Count the number of boxes needed to cover a square contained in (respec-

tively, containing) the disk.

T4.9 1 ⫹ ln 2 ln 3.

T4.10 (b) 1.

T4.11 (a) 0. (b) 1.

4.1 (a) Hint: Deﬁne f(x) ⫽ 3x. Show that f is a one-to-one function from one set

onto the other.

4.2 (a) 1. (b) In base 4 arithmetic, all numbers whose expansions use only 0 and 3.

03, and 17 21 is also in K(4). (d) 0, 1 2. (e) a ⫽ 4.

4.4 Hint: Consider a family 兵Q

其 of intervals such that the nth rational is contained

in Q

and the length of Q

⑀

 (2

), for each n, n ⱖ 1.

4.8 ln 2 ln 3.

4.11 (a) True. Prove for a union of two sets, then generalize. (b) False.

4.12 (a) Hint: Find out the distance between points 1 (n ⫹ 1) and 1 n. Show that

⑀

) ⫽ 2n for

⑀

⫽ 1 n(n ⫹ 1).

4.13 (a) 1/(1⫹p). (b) 0.

T5.1 (2 3)

T5.4 Catmap:2;Ik

eda map: 1 ⫹ .51 .72 ⬇ 1.7.

580

A NSWERS AND H INTS TO S ELECTED E XERCISES

T5.6 (3 4, 1 3) and (1 4, 2 3); there are no others.

5.1 Since J

⫽ Df(v

n⫺1

) ⭈⭈⭈Df(v

), the matrix J

has determinant D

.(The

determinant is unchanged under the transpose operation.) Since the prod-

uct of the m eigenvalues of J

is D

, the product of the semimajor axes

of J

U is r

⭈⭈⭈r

⫽ |D|

. Therefore (r

)

1 n

⭈⭈⭈(r

)

1 n

⫽ |D| for n ⱖ 1, and

⭈⭈⭈L

⫽ [lim

n→

⬁

)

1 n

] ⭈⭈⭈[lim

n→

⬁

)

1 n

] ⫽ |D|, assuming the Lyapunov

numbers exist.

5.2 The Lyapunov numbers will be the absolute values of the eigenvalues of the

symmetric deﬁning matrix, which are (1 ⫾



5) 2. The Lyapunov exponents are

ln(1 ⫹



5) 2 and ln(



5 ⫺ 1) 2. These are smaller than the cat map Lyapunov

exponents by a factor of 2 because the cat map matrix is the square of this one.

5.6 Hint: Design a two-sided symbol sequence that contains every ﬁnite subsequence

of L and R on both sides. There is a positive Lyapunov exponent as explained in

Section 5.6.

5.7 (b) The unit circle r ⫽ 1. (c) Orbits on the unit circle have Lyapunov exponents

ln 2 and ln 2. Orbits inside the unit circle have Lyapunov numbers 0 and 0, so

the Lyapunov exponents do not exist.

T6.2 Yes; consider G(x) ⫽ 4x(1 ⫺ x).

T6.3 (b) Hint: You will need to ﬁnd the symbol sequence of a dense orbit. Any

neighborhood of a point in the invariant set of the horseshoe contains a block

determined by specifying a ﬁnite number of symbols to the left and to the right of

the decimal point. Proceed, as in the construction of a dense orbit for the logistic

map g

, by listing every ﬁnite block of symbols, ordered by length.

T6.6 Hint: Points in the attractor A can be assigned two–sided symbol sequences

just as points in the chaotic set of the horseshoe map. Notice that the orbit of

a point in the solenoid depends entirely on its t coordinate. Speciﬁcally, code

points symbolically by the following rule: the ith symbol is 0 if the t coordinate

of f

(t, z)isin[0,

); otherwise, the ith symbol is 1. Show that any neighborhood

of a point in A can be represented by a symbol block with a ﬁnite number of

symbols speciﬁed to the right and to the left of the decimal point. (The symbols

to the right determine a neighborhood of the t coordinate, while those to the

left determine on which local branch the point is located.) Then follow the

construction for a dense orbit in the horseshoe.

T6.7 Hint: Construct an orbit similar to the dense orbit in the tent map T

or the

logistic map g

, which includes all allowable symbol sequences, ordered by length.

6.1 Hint: See Exercise T6.2.

6.2 Figure 6.10(a): All positive integers. Figure 6.13(a): All positive integers. Figure

6.14(a): All even positive integers.

581