Amaro A., Reed D., Soares P. (editors) Modelling Forest Systems

Подождите немного. Документ загружается.

15Amaro Forests - Chap 13 1/8/03 11:53 am Page 156

16Amaro Forests - Chap 14 25/7/03 11:06 am Page 157

14 An Allometric-Weibull Model for

Interpreting and Predicting the

Dynamics of Foliage Biomass on

Scots Pine Branches

Richard A. Fleming

and Tim R. Burns

Abstract

The foliar biomass dynamics on the branches of young, open-grown, Scots pine (Pinus

sylvestris L.) are modelled as functions of branch length and age. These dynamics are rooted in

a biological foundation by assuming that foliage production depends allometrically on branch

length and that foliage survival on a branch follows an age-dependent Weibull distribution.

Like previously constructed descriptive models, the more process-based model developed here

ﬁtted the data well. In contrast to these purely descriptive models, however, this more process-

based model demonstrated some predictive ability when extrapolated, and produced biologi-

cally meaningful parameter estimates.

Introduction

There are a number of motivations for modelling the foliage biomass dynamics of

trees and of even individual branches. Most motivations derive from an interest in

ecophysiology, growth and yield, and the recognition that foliage constitutes the

photosynthetic engine driving plant growth.

Studies of the impact of different treatments (e.g. partial defoliation, fertiliza-

tion, incr

eased atmospheric CO

, spacing) on the foliage complement are typically

conducted by comparing a ‘control’ or untreated group of trees with corresponding

treated groups (e.g. Ericsson et al., 1985; Långström et al., 1990; Piene and Fleming,

1996; Skre and Nes, 1996; Lyytikäinen-Saarenmaa, 1999). It is often a logistical chal-

lenge, however, to acquire sample sizes large enough to provide such studies with

much statistical power. As big organisms with complex rooting and branching sys-

tems, each individual sampling unit (of one or more trees) requires ample space.

A possible solution is suggested by the observation that trees have a modular

str

ucture where branches may function as more or less independent units. This

offers the possibility of using branches as experimental units instead of whole trees

(Långström et al., 1990; Sprugel et al., 1991, and references therein). By applying

Canadian Forest Service, Great Lakes Forest Research Centre, Canada

Correspondence to: rﬂeming@nrcan.gc.ca

16Amaro Forests - Chap 14 25/7/03 11:06 am Page 158

158 R.A. Fleming and T.R. Burns

treatments to individual branches, the impact on the foliage development of indi-

vidual branches could be studied with less effort than studying the impact on the

foliage development of whole trees. By comparing the development of treated (e.g.

artiﬁcially defoliated) branches on trees with only a few selected branches receiving

treatment with the development of whole trees receiving a whole-tree treatment, the

suitability of individual branches as substitutes for completely treated trees could be

evaluated (Långström et al., 1998).

Measuring treatment effects on the foliage development of a branch requires

accurate estimates of pr

e-treatment foliage biomass. This poses a problem because

accurate estimates of foliage biomass typically require that foliage be removed from

its branch and oven-dried. This precludes measuring pre-treatment (and conse-

quently the change in) foliage dry weight directly, because foliage removal affects

the sample branches and trees and thus confounds the treatment. In addition,

foliage drying is typically very inconvenient and time-consuming.

State of the Art

One approach to getting accurate estimates of pre-treatment foliage biomass is to

use other variables which can be measured non-destructively. For instance, Piene

(1983) estimated the total foliage biomass per branch of 25- to 30-year-old balsam ﬁr

(Abies balsamea (L.) Mill.) using an algorithm that required as input the number of

shoots on the branch, and for each age class of shoot it required the average shoot

and needle lengths and the percentage litter fall. Although much more efﬁcient than

previous methods, Piene’s procedure still relied on detailed information about each

foliage age class on each branch and he found that the predicted foliage biomass

consistently underestimated the actual foliage biomass.

While working with Scots pine (Pinus sylvestris L.), Långström et al. (1998) tried

to further str

eamline the estimation of foliar biomass per branch by using only vari-

ables relevant to the branch as a whole and excluding variables associated with indi-

vidual age classes of foliage. (This use of whole-branch characteristics may be

reliable within the range of the data for conifer species such as balsam ﬁr and Scots

pine, which have regular, orderly branching patterns; it is probably less accurate on

species such as jack pine (Pinus banksiana Lamb.) which branch irregularly.)

Långström et al. (1998) began by assuming an allometric relationship between foliar

biomass and the length of the branch. Recognizing that branch age was also likely to

be a factor, since few Scots pine needles remain longer than 3 years on their branch,

these authors expanded the allometric relationship by incorporating branch age

along with additional powers of branch length to produce a polynomial relationship

with interactions. Accordingly, they expressed the mean foliar biomass, measured as

total needle dry weight (g), on a branch A growing seasons old and of length L (cm) as

(

,YA L

)

= exp

{

b + b L + b A + b

+ b

AL + b A

}

(1)

0 L A A2

This equation was logarithmically transformed to produce a second-order polyno-

mial model which was then ﬁtted by linear regression (Fig. 14.1). The data were

from the undefoliated or ‘control’ trees in their (Långström et al., 1998) study of the

effects of artiﬁcial defoliation on the foliage dynamics of Scots pine (see section on

Data below for more detail). Parameter b

was eliminated because it was not signiﬁ-

cantly (α = 0.05) different from zero. The resulting ﬁve-parameter (transformed)

model ﬁtted the data well: r

= 92.5% and standard error of estimate (SEE) = 0.341.

When the model was extrapolated, however, to estimate the foliage biomass of

unusually lar

ge branches, which are important because they often bear much

16Amaro Forests - Chap 14 25/7/03 11:06 am Page 159

159 Allometric-Weibull Model for Foliage Biomass

expansion of the allometric model (Equation 1) when ﬁtted to only the 77 shortest

potential for extrapolation.

Methodology

The model is developed by thinking of changes in foliage biomass as being the

(triangles, A A

–1

–2

In (foliar biomass (g))

0 25 50 75 100 125

Branch length (cm)

foliage, predictions contradicted biologically based expectations. For instance, the

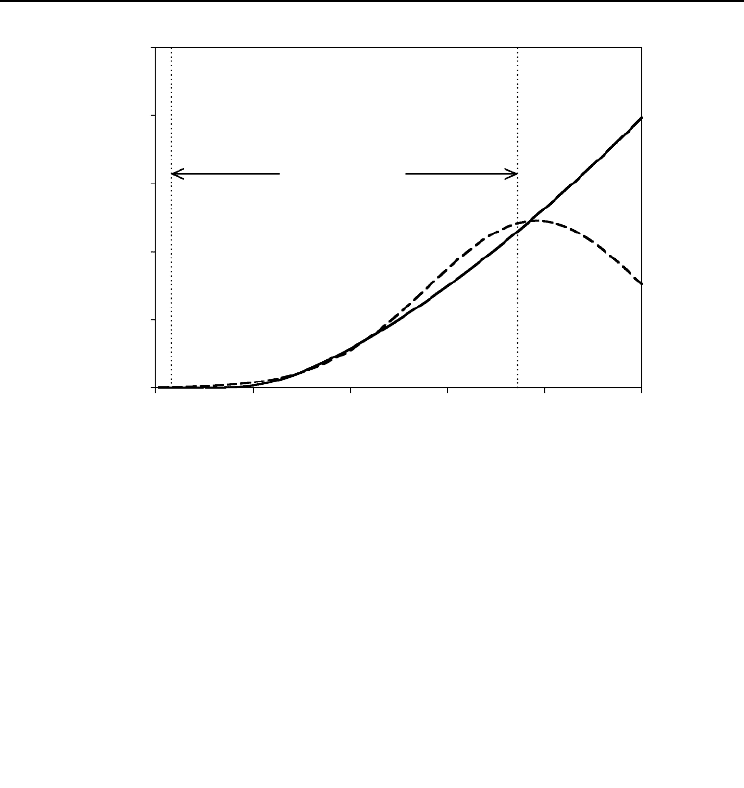
dashed line in Fig. 14.2 shows the predictions of the second-order polynomial

branches. These predictions deviate from the biological expectation of continued

allometric growth for longer branches (see Fig. 14.1). That this dashed line also rep-

resents the corresponding third-order expansion shows that higher order models are

not necessarily better. This long-recognized difﬁculty with polynomial models is

important whenever predictions are needed near the edges of the data or beyond,

and Scots pine branches can exceed 150 cm in length. In what follows, modelling the

foliage biomass of Scots pine branches is pursued with a more process-oriented

approach than used earlier, in the hope of ﬁtting the data well and improving on the

This chapter reﬁnes previous exploratory work (Fleming, 2001) in developing another

approach to modelling relationships between a branch’s length, age and foliar bio-

mass for conifers with regular branching patterns. Ideally such a model will be based

on biological relationships so that its mathematical structure will produce both good

ﬁts to the data and realistic extrapolations beyond the range of the data set. This

approach is applied to the same data used to ﬁt Equation 1.

net result of different demographic processes (Harper and Bell, 1979). Assuming for

the moment that changes in the biomass of individual needles make relatively

minor contributions to changes in foliar biomass, changes in the latter represent the

difference between the biomass of new needles produced each year by the new

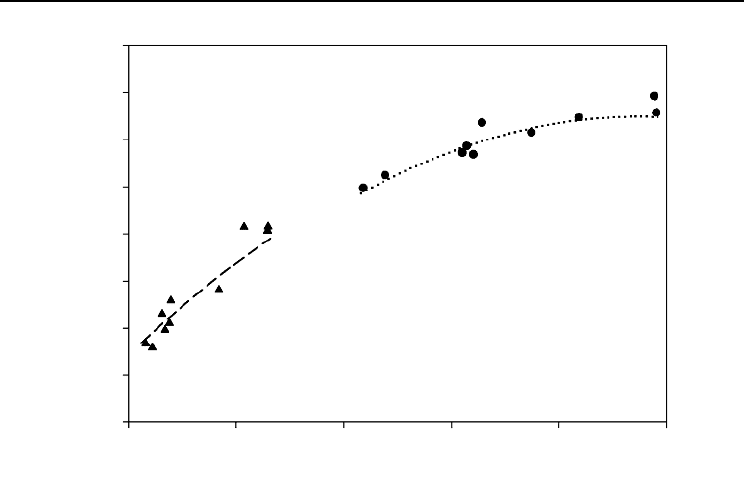
Fig. 14.1. Natural logarithm (ln) of foliar biomass (dry weight) plotted against branch length. The dashed

and dotted curves show the ﬁt of Equation 1 to cross-sections of all ( = 97) data for branches in their ﬁrst

= 0) and ﬁfth (solid circles, = 4) growing seasons, respectively.

16Amaro Forests - Chap 14 25/7/03 11:06 am Page 160

160 R.A. Fleming and T.R. Burns

shoots on the branch and the mortality of needles as they age. Hence, following

Långström et al

tion of branch length, and following Fleming and Piene (1992a,b), it is assumed that

an age-dependent population survival model can describe needle survival on the

branch. Putting these two assumptions into mathematical form and adopting the

independent, the foliar biomass (g) on a branch of age A

length L cm can be written:

(2)

The factor P(L

branch. P(L) is assumed to be an allometric function of L, the length (cm) of the

branch, so that

(3)

w = P(1) > 0 (P(1) = P(L) when L = 1) and c

the speciﬁc rate of change in P(L

speciﬁc rate of change of length: dP(L)/P(L) = (c+1) dL/L

if c

length, branch age, A

of similar length (Fig. 14.3).

()

( )

()( )

range of

observations

Branch length (cm)

50 75 100 125250

125

100

Foliar biomass (g)

. (1998), it is assumed that needle production is an allometric func-

simplifying assumption that the processes of needle production and survival are

growing seasons and

) represents the dry weight of needles produced over the years on the

where represents a constant. This equa-

tion satisﬁes the deﬁnition for allometric growth (Pienaar and Turnbull, 1973) in that

) bears a constant proportional relationship to the

where d represents the dif-

ferential operator. (The ‘+1’ in the exponent is convenient for parameter estimation:

is not signiﬁcantly different from 0 then the corresponding exponent can be con-

sidered equal to 1 and dropped.)

When comparing the foliage productivity of different branches of the same

, becomes an additional consideration. Younger branches have

less time than older branches to build networks of side branches. Side branches pro-

vide extra surface area for growing foliage, so young branches of a given length

tend to have less branch surface area on which to grow foliage than older branches

YA L P L S A

Fig. 14.2. Predictions of the models when ﬁtted to the 77 shortest branches. Branch age is ﬁxed at its mean,

= 4.12 years. The dashed curve represents the second- (Equation 1) and third-order polynomial

expansions of the allometric model. The solid curve illustrates the corresponding basic allometric growth.

16Amaro Forests - Chap 14 25/7/03 11:06 am Page 161

161 Allometric-Weibull Model for Foliage Biomass

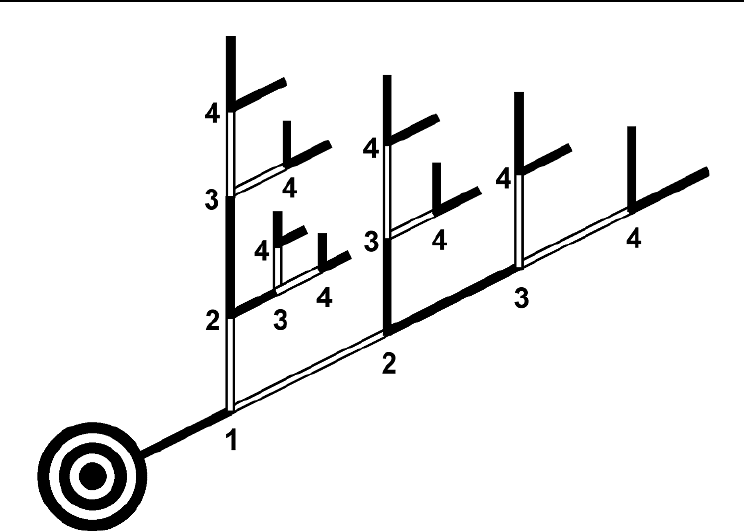
Fig. 14.3. Schematic of a 5-year-old Scots pine branch (after Flower-Ellis et al., 1976; Långström, 1980).

Numbers 1–4 at forks indicate cumulative growth along the main and side axes over each of the branch’s

ﬁrst four growing seasons. The ﬁnal increments beyond the last (A = 4) forks were added in the ﬁfth growing

season and represent the youngest shoots.

In contrast, although the very oldest branches may have extensive networks of

side branches, they occur at the base of the crown (Fig. 14.4) where light is more lim-

ited. Under limited light, a decline in foliage production rates (per unit branch sur-

face area) is conceivable. For these reasons, the expression for foliage productivity

was expanded beyond its basic allometric form to

cA+1

PAL

)

= wAL

(

()

(4)

where w

(A) = P(A,1) > 0 (P(A,1) = P(A, L) when L=1) and c(A) now represents

unspeciﬁed functions of branch age. The biology of foliage development on growing

branches restricts the range of the allometric function, c(A). Branches tend to grow

side branches as they age (Fig. 14.3), so long branches tend to have disproportion-

ately more available surface area than short branches for growing foliage.

Accordingly, c(A) > 0.

In Equation 2, S(A) represents the proportion of the foliage surviving on

branches of age

A. The Weibull model was adopted to approximate S(A) because:

(i) it is relatively simple and ﬂexible when compared with other survivorship mod-

els (Kalbﬂeisch and Pr

entice, 1980), and (ii) it has been successfully applied to

foliage survivorship in other conifers (Fleming and Piene, 1992a,b; Piene and

Fleming, 1996). Therefore, we model the proportion of the original foliage biomass

surviving on a branch of age A as

v+1

}

()

= exp

{

−

(

A u

)

(5)

where u > 0 and

v > 1 represent constants.

16Amaro Forests - Chap 14 25/7/03 11:06 am Page 162

162 R.A. Fleming and T.R. Burns

branch length, with the uppermost branches being particularly vulnerable.

weight of foliage on a branch of age A and length L:

(6)

w(A) and c(A

After explicitly writing in the linear functions, Equation 6 was

, exp /

( )

()

−

( )

{ }

()

Shoot age

54321

Branch age

et al.

the bottom.

Branch length has been considered a factor when comparing foliage survival on

branches produced in the same year. Fleming (2001) noted that foliage on the

longest branches, especially on the outer extremities of those branches, is exposed to

foliar mortality agents such as freezing rain and high winds. However, for open-

grown trees, branch height is thought to be more important in this regard than

Therefore, since a branch’s height (crown position) is closely related to its age (Fig.

14.4), it is reasonable to initially and tentatively assume that foliage survival can be

largely explained by branch age alone. (An added beneﬁt of this assumption is that

it simpliﬁes model ﬁtting.) Consequently, Equations 4 and 5 were substituted into

Equation 2 to produce an allometric-Weibull model to approximate the total dry

For simplicity, we assume that ) are linear. (More complex rela-

tionships can be entertained later if this simple approach does not prove satisfac-

tory.)

log-transformed to produce homogeneity of variance in the dependent variable

and symmetry of the residuals. Non-linear regression was used to ﬁt the resulting

log-transformed equation. This process involved recursive model building and the

application of a pseudo Gauss–Newton algorithm for non-linear least squares esti-

YAL wAL A u

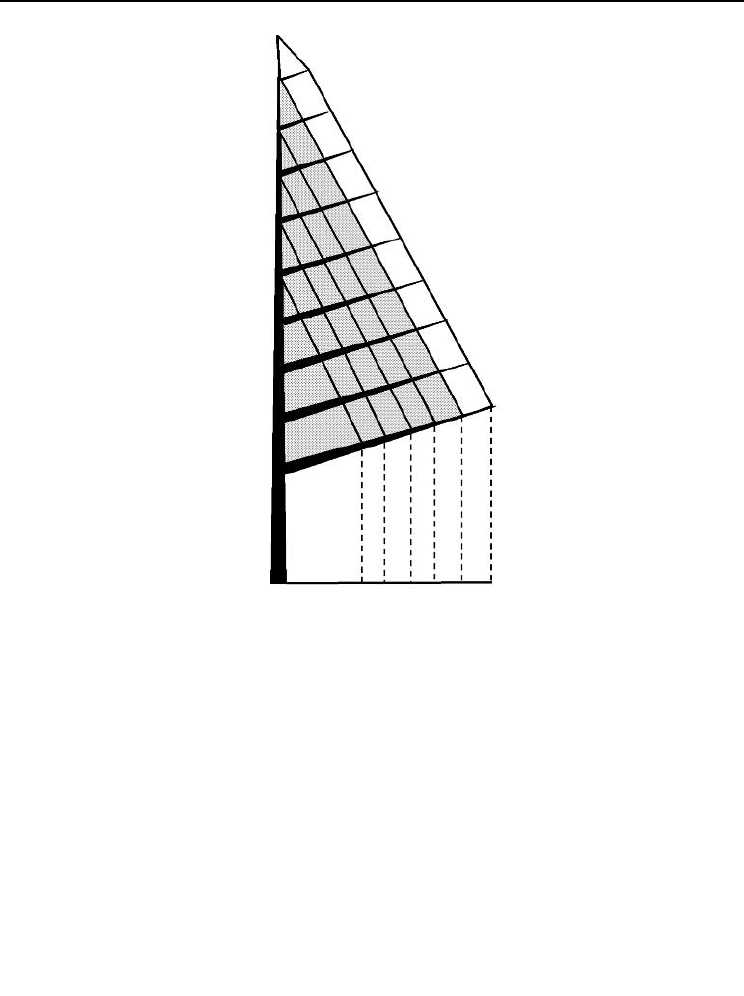
Fig. 14.4. Schematic of a 10-year-old Scots pine (after Ericsson , 1980). Branch ages in completed

growing seasons are shown vertically on the right. Ages of shoots on the main branch axis are shown along

16Amaro Forests - Chap 14 25/7/03 11:06 am Page 163

163 Allometric-Weibull Model for Foliage Biomass

mation (Ralston, 1992) of each model constructed. At each stage in this recursive

process, parameters with estimates not signiﬁcantly different from zero (α = 0.05)

according to the partial F-test (Draper and Smith, 1981) were removed and the

reduced model reﬁtted. This procedure was continued until only parameters with

statistically signiﬁcant estimates remained. Residual distributions and residuals

plotted against predictions and predictor variables were examined to verify rea-

sonable compliance with the assumptions of regression.

Predicted values resulting from ﬁtting the log-transformation of Equation 6 are

not dir

ectly useful because they represent geometric means and it is arithmetic

means that are needed. To get arithmetic predicted means, the ﬁtted equation must

be back-transformed and the right side multiplied by the correction factor (Sprugel,

1983), exp{

SEE

/2}. Then the (arithmetic) mean foliar biomass (g dry weight) for a

branch L cm long and A years of age can be predicted by substituting the parameter

estimates and

SEE (standard error of estimate) from ﬁtting the log-transformation of

Equation 6 into the general expression,

v+1

YA L

)

= exp ln

(

w + w

)

(

c + + c

)

()

−

(

A / u

)

SEE

/ 2

}

(7)

(

{

0 0

Test of extrapolation reliability

It was suggested above, in the context of Fig. 14.2, that the two ﬁtted polynomial

expansions of allometric gr

owth appeared less biologically plausible than the more

process-oriented, allometric-Weibull model when extrapolated to large branches. To

test this notion more thoroughly, these three models were each ﬁtted to the observa-

tions from the 77 shortest (L < 93 cm) branches as described above. By inputting

appropriate combinations of A and L, predictions were obtained from each model

for the 20 longest branches (93 cm < L < 125 cm) in the data set. This amounted to

extrapolating each model up to 34.4% beyond the range of the data used for ﬁtting.

The extrapolated predictions were compared with the observed foliar biomass

of the 20 longest branches to estimate the r

elative reliability of each model for

extrapolation. Three options for estimating bias were considered (Zar, 1996). The

paired t-test was applied if the deviations (observations  corresponding predic-

tions from extrapolation) had approximately normal distributions. Otherwise, if the

variance of the extrapolated predictions did not differ substantially from the vari-

ance of the observations, the Mann–Whitney test (Mann and Whitney, 1947) was

applied. Failing that, a two-sample t-test without pooled variances was applied.

Data

The data were produced in an artiﬁcial defoliation study (Långström et al., 1998)

conducted at Ivantjärnsheden, Jädraås, in central Sweden, about 200 km north-west

of Stockholm (61° N, 16° E, 185 m above sea level). The site was in a heath Scots pine

forest, of dry dwarf shrub type, with a podzolic soil proﬁle. (Axelsson and

Bråkenhielm (1980) provide a detailed description of the area.) The site had been

clearcut in 1971, and planted in 1972 with Scots pine seedlings of local provenance

at 2000 seedlings per hectare. Naturally regenerated pine seedlings had developed

in gaps following seedling mortality. The stand was cleaned in 1985 to about 1500

stems per hectare, and by spring 1991, was a pure pine stand with some open

patches.

16Amaro Forests - Chap 14 25/7/03 11:06 am Page 164

164 R.A. Fleming and T.R. Burns

The 97 observations used in this chapter were made on open-grown, untreated

(i.e. ‘control’) Scots pines in August 1991, at the end of the growing season that year.

The data consist of branch lengths and corr

esponding foliage biomasses for

branches which had experienced 1–10 full growing seasons (i.e. ages A = 1–10).

These data were supplemented by observations taken in June 1991, before the 1991

growing season, on branches initiated in 1990. These supplementary observations

provide information on new branches (age A = 0) but their use requires the assump-

tion that foliage losses from these new branches were minimal in the winter of

1990/91.

Results

Fitting the allometric-Weibull model, Equation 6, after log-transformation, to all 97

observations resulted in

SEE = 0.343 and a pseudo r

(Ralston, 1992) of 92.4%. The

estimates of the statistically signiﬁcant parameters, their

SEs (standard errors) and

their P values were w

= 0.0799 (SE = 0.0246, P = 0.0016), c

= 0.279 (SE = 0.1060, P =

0.01), c

= 0.237 (SE = 0.0327, P < 0.0001), u = 1.57 (SE = 0.226, P < 0.0001) and v =

0.312 (

SE = 0.0638, P < 0.0001). According to these results, foliage biomass is pre-

dicted to increase allometrically with branch length on branches of all ages and the

rate of this allometric increase depends on branch age (Fleming, 2001; Fig. 14.3). It is

slow on old branches, presumably because of high foliage losses. It is also slow on

very young branches, presumably because such branches have had little time to

develop extensive networks of lower order side branches which provide much addi-

tional surface for growing foliage (Långström et al., 1998). The youngest branches

also occupy some of the most exposed parts of the crown where their foliage may be

especially vulnerable to mortality from freezing rain or high winds. The low foliar

biomass on very short branches may be because these branches are very young, are

shaded by overhanging branches or were broken off before the data were collected,

and much foliage was lost when this happened.

To gauge the adequacy of Equation 7, a predicted arithmetic mean was calcu-

lated using the values of

A and L corresponding to each observation. The r

value

(i.e. the square of the Pearson correlation coefﬁcient between the observations) and

these pr

edictions was 85.4%. The 97 paired differences were not normally distrib-

uted (P < 0.0005) and the variances of the distributions of observations and predic-

tions differed little (P = 0.909), so the Mann–Whitney test was applied to reveal bias.

The high P value (0.810) of this test is consistent with the practical absence of statis-

tically signiﬁcant bias. The solid curve in Fig. 14.2 shows the allometric growth pre-

dicted by ﬁxing A at its average, 4.12 growing seasons, and substituting the

estimated parameter values into Equation 7.

Extrapolation reliability

In ﬁtting both the second- (Equation 1) and third-order polynomial expansions of

allometric gr

owth to the 77 shortest branches, six parameters were statistically sig-

niﬁcant, and hence were retained. Only parameters w

, c

, u and v were retained in

ﬁtting the allometric-Weibull model. Characteristics (

SEE, r

) of ﬁtting log-transfor-

mations of these models were: second-order polynomial (Equation 1) (0.349 g,

91.8%), third-order polynomial (0.340 g, 92.2%) and allometric-Weibull model (0.374

g, 90.3%). Table 14.1 gives the results of comparing extrapolations of these ﬁts to the

20 longest branches.

16Amaro Forests - Chap 14 25/7/03 11:06 am Page 165

165 Allometric-Weibull Model for Foliage Biomass

Table 14.1. Performance of model ﬁts to the 77 shortest (L

≤ 93 cm) branches when extrapolated to the

20 longest (93 cm ≤ L ≤ 125 cm) branches.

Deviations Extrapolations

(observation  extrapolated

prediction)

Model Standard Equal Two-sample Pearson

mean error Normal?

variances?

t-test

correlation

2nd-order polynomial 13.4 g 6.43 g P = 0.012 P = 0.062 P = 0.041 r =0.102 P =0.670

expansion

3rd-order polynomial 13.2 g 6.86 g P = 0.055 P = 0.053 P = 0.066 r =0.004 P =0.986

expansion

Allometric-Weibull 2.96 g 4.87 g P = 0.045 P = 0.084 P = 0.639 r =0.533 P =0.015

model

Anderson–Darling test (Anderson and Darling, 1954).

Levene’s test (Levene, 1960).

Without pooled variances.

Discussion and Conclusions

Table 14.1 shows that the allometric-Weibull model provides a more reliable basis

for extrapolating to large branches than using polynomial expansions of allometric

relationships such as Equation 1. Together, the mean deviations and the results of

the two-sample t-tests show tendencies for the polynomial expansions to underesti-

mate the foliage biomass of long branches. In contrast, for the allometric-Weibull

model, the relatively high P value of its two-sample t-test and its relatively low

mean deviation provide no indication of bias. The correlation coefﬁcients and their

associated P values show that: (i) the extrapolated polynomial expansions provide

little information about trends in foliage biomass for long branches, while (ii) the

allometric-Weibull still explains a statistically signiﬁcant part of the variation in

foliage biomass when extrapolated to the 20 longest branches. Clearly, the allomet-

ric-Weibull model is an improvement on the polynomial approach, but these results

also indicate the dangers of extrapolating: the model’s r

is 84.2% when ﬁtted to the

77 shortest branches but falls to 28.4% when extrapolated to the 20 longest.

One advantage of using well-studied models for constructing subcomponents

of lar

ger models is that it can simplify the interpretation of results. In developing the

model presented in Equation 6, the Weibull distribution model was used to describe

the process of foliage mortality/survival on a branch (Equation 5). Because changes

to v and u, respectively, do and do not affect the distribution’s shape, they have

become known as the ‘shape’ and ‘scale’ parameters.

In our case, v > 0 (P < 0.0001), so the age-speciﬁc mortality rate increases monot-

onically and asymptotically with age towar

ds its maximum. This situation occurs in

many ageing populations in which individuals suffer ‘wear-out’ or ‘old age’ effects.

Since it was branch age, not foliage age, that was recorded, inferences about the dis-

tribution of foliage longevities must be made in terms of branch age. For instance,

v > 0 indicates that rates of branch age-speciﬁc foliage survivorship decreased with

branch age.

Finally, that c

was signiﬁcantly greater than zero suggests that foliar produc-

tion increased with branch age. This implies that the tendency for very young

branches to have relatively restricted networks of lower order side branches (and

thus relatively little potential branch surface on which to grow foliage per unit