Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


150
Andrea
Donato
In the case of parabolic equations, the effect of nonlinearity is
balanced by dispersive
or
dissipative effects. The major problem in
the study
of
nonlinear wave phenomena is related
to
the
loss
of the
principle
of
superposition.
In the sequel we are mainly interested on the propagation
of
weak
discontinuities compatible with first order quasilinear hyperbolic sys-
tems. These are piece-wise continuous solutions with discontinuities
in the first order derivatives occurring across
a
smooth surface said
the wave front. Such kind of discontinuities may occur only
across
characteristic surfaces which evolve in time. Ahead
of
the wave front
we have the “undisturbed solution” characterized by some known
solution, whilst on the other side we have the unknown perturbed
solution.
There exists
a
large literature concerning the propagation of weak
discontinuities in many physical contexts. In dealing with applica-
tions, the “unperturbed state” is very often considered
a
“constant
state”
as
the most simple solution of the nonlinear governing equa-
tions. On the other hand it is well known the difficulty to characterize
solutions
of
nonlinear systems.
A systematic approach in order to characterize exact solutions
of
partial differential equations is the group analysis that in the mean-
time allows
us
to put in evidence physical symmetries. The partic-
ular solutions
so
obtained usually referred to
as
similarity solutions
are restricted in the sense that they must satisfy special initial and
boundary conditions. Nevertheless they play an important role
as
a
vehicle of information for the description of more general physical
contexts.
Similarity solutions arise in
a
natural way in axi-symnmetric
problems
as
well
as
in regions with inhomogeneities. Two orders
of problems may be considered. First we
ask
the possibility of
wave propagation compatible with the similarity assumptions and
whether, in the one-dimensional case, the similarity lines may be
considered
as
discontinuity lines across which the jump conditions in-
volve similarity variables only.
As
a
second problem we are interested
to consider the propagation of weak discontinuities in
a
non-constant
state characterized by
a
known similarity solution.

Nonlinear Waves
151
Studies
of
blast waves in fluids give rise
to
problems of this type
and the occurrence of
a
secondary shock can be determined.
In both the above mentioned problems the canonical variables
play
a
fundamental role. In terms
of
these variables the transforma-
tion group admitted by the governing system may be expressed
as
a
traslation. When the group of invariance is the dilatation group, by
using in
a
proper way the canonical variables, the constant solution
of
the transformed system may appear to be
a
special non-constant
solution in the original variables.
Consequently, the procedure outlined allows not only to study
wave propagation into
a
“non-constant state”
as
a
propagation into
a
“constant state” in the new variables, but also to characterize special
similarity solutions. The usual invariant solutions are characterized
as
stationary solutions
of
the transformed system.
2
Hyperbolicity
Wave phenomena of hyperbolic type are described by first order
quasilinear systems
of
equations in matrix form, namely:
where u(x,t) is an unknown column vector with elements (ul(x,t),
uZ(x,t),
. .
.,
uN(x,t)) defined for
x
=
(q,x2,.
. .
,z,)
E
Rn,
t
E
R+.
The
N
x
N
matrices
A”
(a
=
O,l,
2,.
. .
,
n) and the column vector
B
of
N
elements axe assumed given. On introduction of the matrix
A,
=
C%l
A’n;
,
n
E
Rn
then we introduce the following definition:
Definition
1
The system
1
is
said
to
be
hyperbolic in the t-direction
if
det(Ao)
#
0
(2)
A,dK
=
XAOdK
(3)
and the eigenvalue pmblem
has,
for
every
n
E
R”,
only
real
eigenwalues X(u,n) and
a
cow-
sponding complete family
of
right eigenuectors
dK(
u, n) together with

152
Andrea
Donato
a
complete family
of
left eigenvectors
lj
satisfying
ljA,
=
&Ao
,
(4)
(J,
K
=
1,2,.
. .
,p
if
X
has multiplicity
p).
The system is said to
be
strictly hyperbolic if, moreover,
det(A,
-
XAO)
=
0
(5)
has
N
distinct real mots.
The hyperbolicity
so
defined depends not only on the point
(x,
t)
E
R"
x
R+
but also on the solution
u(x,
t).
Moreover, the assumed con-
ditions constitute
a
necessary requirement
for
the Cauchy problem
for
the system
1
to be well posed
[l].
Physical processes are commonly modeled by balance laws
OF0(u)
OF'(u)
at
OX'
+--
-
f(u)
which involve the unknown field
u(x,t).
These are particular cases
of
the system
1
when
:
Important examples
of
such conservation laws occur in gas dy-
namics, magnetofluid dynamics and nonlinear elasticity ([2],
[3],
[4],
If
the matrices
A*
are symmetric and, moreover,
Ao
is definite
positive then, by elementary linear algebra, it may be seen that the
system 6 that results is automatically hyperbolic.
For
such
a
system
the resulting Cauchy problem is locally well-posed under suitable
smooth initial data
[7].
We now assume that the system 6 is compatible with
a
supple-
mentary scalar conservation law:
[51,[61).
Oh(u) Ohi(u)
at
OX'
+--
-
9w

Nonlinear Waves
153
where
h(u)
is
a
strictly convex function of the field
u
in some open
domain.
This requirement
is
often fulfilled in dealing with physical models.
Thus,
a
conservation law such
as
8
arises
as
the
Entropy Principle
in
Continuum Mechanics when
g
5
0
or
as
the
energy equation
in the
Maxwell system of the Electromagnetic theory. Scalar
conservation
laws
derived from variational principles also adopt such
a
form
[8].
The equation
8
may be considered
as
a
differential constraint
to be satisfied by the solutions of the system
6.
Restrictions on
the structure of the system are thereby implied. Such problems have
been studied in
[9],
[lo],
[ll],
[12],
(131.
As
A0
is non-singular we may
choose
v
=
Fo(u)
as
field variable and the compatibility conditions
of
6
and
8
are:
On introduction
of
the transformation
of
variables
:
This is
a
symmetric and hyperbolic system.
forces take the form
6
with
The Euler equations for ideal
Gas
Dynamics neglecting external

154
Andrea
Donato
where
c
=
w2/2
+
pe,
i
=
e
+
p/p,
di
=
Tds
+
dp/p,
q
is the
particle velocity,
i
the enthalpy,
p(p,e)
the pressure depending on
the density
p
and the internal energy
e
of the fluid;
T
will be the
absolute temperature and
S(p,
e)
the entropy.
The supplementary conservation law
to
be associated to the sys-
tem in this special case
is
of the form
8
with:
h
=
-pS
hi
=
-pSqi
g=o
(14)
expressing the law of conservation of entropy.
Taking into account that
TdS=de-Tdp
P
,
P
the following relation is valid:
q2
Tdh
=
qd(pq)
+
(G
-
-)dp
-
dc
2
where
G
=
i
-
TS
is the free enthalpy.
Consequently, by
11
we obtain:
The function
h
may be shown
[14]
to
be
a
convex function
of
the
field variables under the usual restrictions
for
a
gas in the thermo-
dynamic equilibrium. Again, by
11
it follows:
3
Discontinuity
waves
The condition det(Ao)
#
0
valid for hyperbolic systems allows us, by
multiplying
1
by the inverse matrix (Ao)-', to write the system
as:
aU
au
-
+
A'(u)-
=
B(u,x,t)
at
ax;

Nonlinear Waves
155
where now
A'(u,x,t)
and
B(u,x,t)
are
the result
of
the original
quantities multiplied by
(
Ao)-'.
For
simplicity we assume that the matrices
A'
do not depend on
x
and
2.
Consider
a
smooth moving surface
4(x,t)
=
0
(wave front)
separating
R"
x
R+
into two subspaces in each of which
u(x,t)
is
a
C'
function
of
its arguments. Ahead
of
the wave front we have
a
known solution
uo(x,t)
and behind the wave front the unknown
perturbed field
u(x,t).
Across the wave front
u
=
~0
but there are
discontinuities in the first order derivatives along the normal to the
wave front.
If
the jump is denoted by
then
(21)
8U
u
-
uo
=
[u]
=
0
[Sl=n#o
The normal speed
of
propagation and the unit normal vector of
the wave front are:
an=X=
dt
-&,
4t
=
g
n=
The well known Hadamard relations now yield:
[%I
=
4tn
[2]
=
gradfjm
(23)
On use
of
23
and
24
in
19
we readily obtain the following compati-
bility conditions to be satisfied by the discontinuity vector
n:
The normal velocities
X
are found
as
eigenvalues
of
the matrix
Ao,
=
A,(uo)
evaluated in
UO(X,~),
the known unperturbed field, while
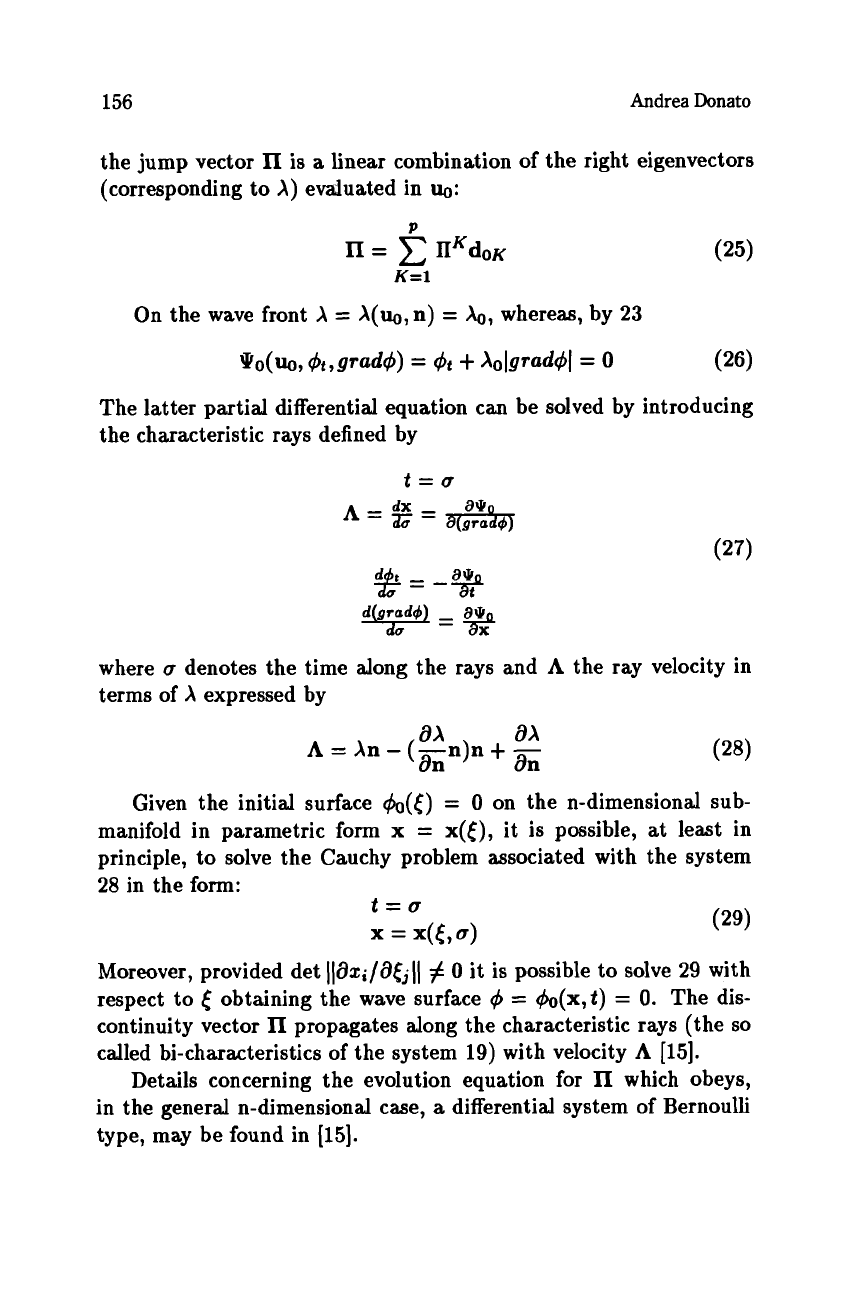
156
Andrea
Donato
the jump vector
lI
is
a
linear combination
of
the right eigenvectors
(corresponding
to
A) evaluated in
uo:
P
On the wave front
X
=
A(uo,n)
=
&,
whereas, by
23
~o(uo,q5t,graW
=
9:
t
Aolgradq5I
=
0
(26)
The latter partial differential equation can be solved by introducing
the characteristic rays defined by
where
a
denotes the time along the rays and
A
the ray velocity in
terms of
X
expressed by
ax
ax
A
=
An
-
(-n)n
+
-
an On
Given the initial surface
&(t)
=
0
on the n-dimensional sub-
manifold in parametric form
x
=
x(t),
it is possible,
at
least in
principle,
to
solve the Cauchy problem associated with the system
28
in the form:
Moreover, provided det
Ilaz;/a(jjll
#
0
it is possible
to
solve
29
with
respect to
t
obtaining the wave surface
q5
=
&(x,t)
=
0.
The dis-
continuity vector
lI
propagates along the characteristic rays (the
so
called bi-characteristics of the system
19)
with velocity
A
[15].
Details concerning the evolution equation for
n
which obeys,
in the general n-dimensional case,
a
differential system of Bernoulli
type, may be found in
[15].

Nonlinear Waves
157
In the one-dimensional case, that will be considered in the sequel,
the evolution law for the components of
ll
in
25
is
[16]:
AOZK~
+
AOZK~~~J~J~K
t
~ZK~K
=
0
(30)
dHK
where
AOZK
=
bZdOK
az
=
(&dz)o
z=;7i+%
(31)
a1
T
-
a1
du
d)z
+*
-
&(lZB)dK
+
lZ+z)o
ad
du
hZK
=
((lZ%)(gdK)
+
dK((d)
da
Since the system
19
is hyperbolic, the matrix
AOZK
=
lozdoK
must be non-singular and the left and the right eigenvectors may be
chosen in order that it becomes the unitary matrix. The system of
equations may be formally integrated
to
give
VK
Q
nK
=
-
where
qK
and
Q
are solutions of the following ordinary differential
equations:
%
t
hKZ(a)VZ
=
0
$$
+
42azvz
=
0
(33)
qK(0)
=
nK(0)
4(0)
=
1
where
4x
,
by
28,
satisfies
For
strictly hyperbolic systems
or
for systems with
a
characteris-
tic velocity
of
multiplicity
1
we have simply (choosing
A
=
bdo
=
1):
(35)
II(0)
exp(-
J:
h(a)da
1
+
n(0)
J:
a(a)4,
exp(-
&'
h(s)ds)da
n=

158
Andrea
Donato
It can be easily shown that if
al
#
0
there may exist
a
time
t,
such that the denominator
of
32
vanishes and the discontinuities
become unbounded.
This corresponds, usually, to the formation of shocks resulting
from the non-linearity.
A
discontinuity wave propagating with ve-
locity
X
such that
al
=
Ed1
=
0
is said an
exceptional wave
since
the discontinuity behaves
as
in the linear case. It is worthwhile to
note that, for conservative systems, every discontinuity wave hav-
ing
a
multiplicity more than one is exceptional [17], [MI. This is
illustrated by material waves in three-dimensional fluid dynamics.
We remark that
all
the above considerations are
of
practical in-
terest if
a
solution
uo(x,t)
in the unperturbed state is known. The
most obvious solutions to seek are constant solutions satisfying the
condition
B(u0)
=
0.
These
are
common in the literature. Here,
however, we would like to consider the case when the propagation is
into
a
non-constant state characterized by an exact solution
of
the
system 19 invariant with respect to
a
one-parameter group of trans-
formations corresponding to the stretching group. Problems such
as
these arise in the analysis
of
wave propagation in media with cylindri-
cal
or
spherical symmetry
as
well
as
in regions with inhomogeneities
~41,
~91,
POI
4
Canonical variables
Here we limit ourselves to one-dimensional problems described by
first order systems in the form
These we assume to be invariant with respect to
a
one-parameter in-
finitesimal group of transformations characterized by the generators:
T
=
T(x,t,u)
x
=
X(x,t,u)
17
=
177(2,t,U)
(37)

Nonlinear
Waves
159
This allows us to find the finite invariance group
G:
t*
=
t*(s,t,u;€)
x*
=
x*(s,t,U;€)
(38)
u*
=
U*(s,t,U;€)
by solving
a
Cauchy problem
as
is stated by Lie's theorem
[21],
(221,
In principle it is always possible
to
consider
a
canonical transfor-
~31.
mation:
7
=
7(2,t,U)
t
=
5(3,t,U)
w
=
W(Z,t,U)
(39)
in terms
of
which the group
G
reduces simply to
a
translation in the
variable
7:
7*
=
T+€
t*
=
t
w*
=
w
and the associated generators are
:
0=1
x=o
r=o
The infinitesimal operator
of
the group
G
in the new variables becomes
