Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.

170
Andrea
Donato
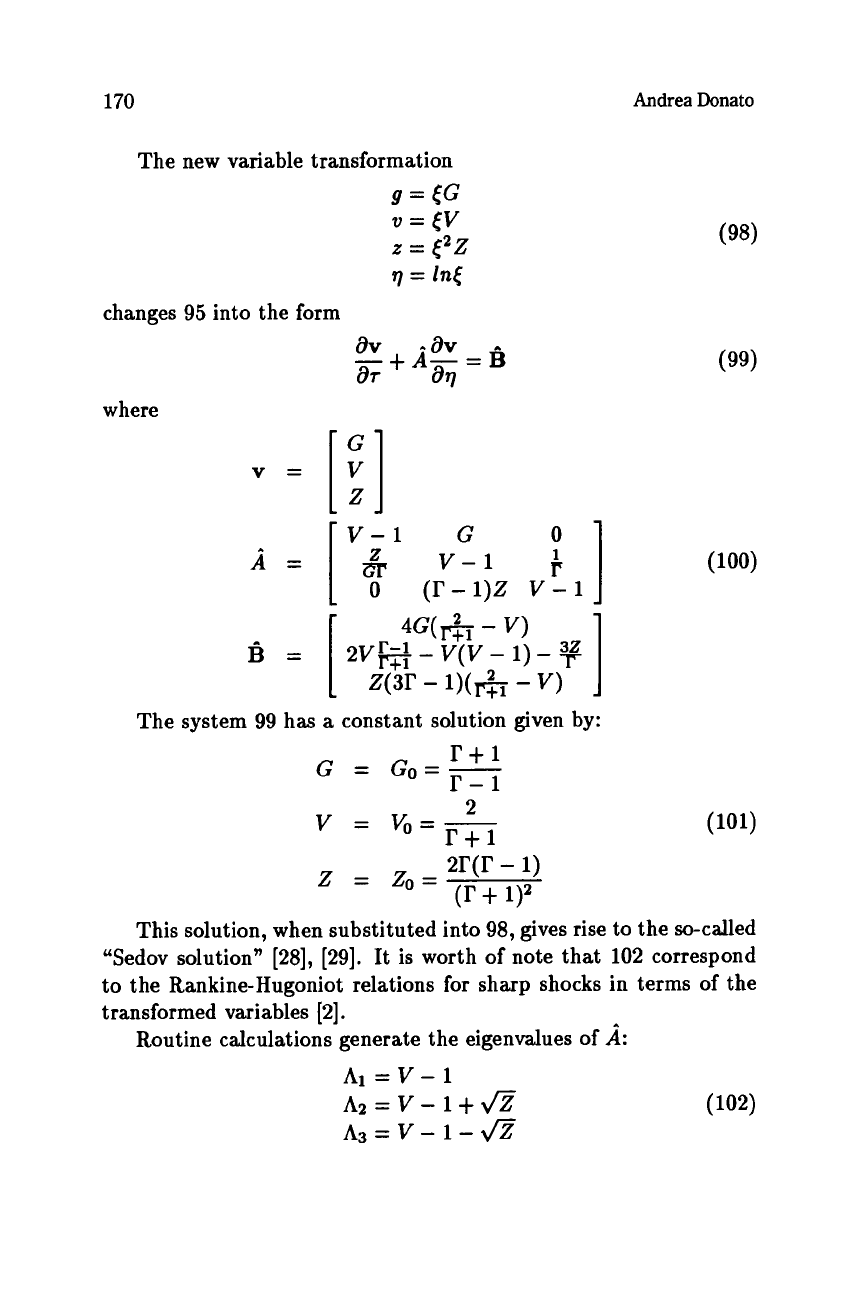
The new variable transformation
9
=
tG
v=[V
z
=
pz
q
=
In(
av
-av
a7
aq
changes
95
into the form
-+A-=B
where
v
=
[;I
v-1
G
v-1
;
]
1
o
(r-1)~
v-i
The system
99
has
a
constant solution given by:
(99)
This solution, when substituted into
98,
gives rise to the so-called
"Sedov solution"
[28], [29].
It
is
worth of note that
102
correspond
to the Rankine-Hugoniot relations for sharp shocks in terms of the
transformed variables
[2].
Routine calculations generate the eigenvalues
of
a:
Al=V-l
A3
=
V-
1
-
&
A2
=
V
-
1
+
&
(102)

Nonlinear Waves
171
The values
a-,
and
ho
occurring in
85
corresponding to
A2
and
A3
are, respectively
(1
t
r)@O
2(3r
-
1)
@,/-
t
3r
-
5
2(3r
-
1)
a0
=
f
(103)
ho
=
-
that allow us to obtain, because
of
86
the critical time when the
secondary shock would appear.
For
the special value of
I'
=
1.0463
corresponding to the char-
acteristic propagating with the velocity
A2,
we get
a0
=
0.148479.
Consequently, the evolution
of
the discontinuity is completely deter-
mined by
(5.3)
in this special case.
Other physical examples where the above mentioned procedure
to study the propagation
of
weak discontinuities in
a
non-constant
state characterized by
a
similarity solution may be found in
[30], [31],
[32l, P31.
Bibliography
A.
Jeffrey,
Quasi-linear hyperbolic systems and waves,
Research
Notes in Mathematics
5,
Pitman Publishing, London
1976.
G.
B.
Whitham,
Linear and nonlinear waves,
John Wiley and
Sons, New York,
1974.
R.
Courant and
K.
0.
Fkiedrichs,
Supersonic flow and shock
waves,
Interscience Publishers Inc., New York,
1967.
B.
L.
Rozdestvenskii and
N.
N.
Janenko,
Systems
of
Quasilinear
Equations and Their Applications to Gas Dynamics,
Transla-
tions of Mathematical Monographs,
55,
A.M.S.,
1983.
A.
Majda,
Compressible Fluid Flow ans Systems
of
Conserva-
tion Laws in Seveml Space Variables,
Applied Mathematical Sci-
ences,
53,
Springer-Verlag, New York,
1984.

172
Andrea
Donato
[6]
A. Jeffrey and
T.
Taniuti,
Nonlinear wave propagation,
Acca-
demic Press,
New
York,
1964.
[7]
A. Fischer and D.
P.
Marsden,
The Einstein evolution equations
as
a
first order quasilinear simmetric hyperbolic system,
Comm.
Math. Phys.,
28
p.
1-38, 1972.
(81
S.
K.
Godunov,
An interesting class
of
quasilinear systems,
Sov.
Math.,
2,
p.
947-949, 1961.
[9]
K.
0.
Friedrichs and
P.
D.
Lax,
Systems
of
conservations equa-
tions with
a
convex exstension,
Proc. Nat. Acad. Sc. USA,
68,
p.
1686-1688, 1971.
[lo]
G. Boillat,
Sur l’kxistence et
la
recherche d’kquations de conser-
vation supplementaires pour les systkmes hyperboliques,
C. R.
Acad. Sci. Paris,
278A,
p.
909-912, 1974.
[ll]
G.
Boillat and
T.
Ruggeri,
Simmetric form
of
nonlinear me-
chanics equations and entropy growth acmss
a
shock,
Acta Me-
chanica,
35,
p.
271-274, 1980.
[12]
T.
Ruggeri,
Symmetric hyperbolic system
of
conservative equa-
tions
for
a
viscous heat conducting fluid,
Acta Mechanica,
47,
p.
167-183,1983.
[13]
A.
Donato,
On
a
supplementary conservation
law
for
the balance
laws in thermoelastic bodies,
Meccanica,
10,
p.
229-232, 1983.
[14]
D. Fusco,
Alcune considemzioni sulle onde d’urto in
fluidodi-
namica,
Atti Sem. Mat. Fis. Univ. Modena,
28,
p.
223-236,
1979.
[15]
G. Boillat,
La
propagation des ondes,
Gauthier-Villars, Paris,
1965.
[16]
G. Boillat and
T.
Ruggeri,
On the evolution
law
of
weak discon-
tinuites
for
hyperbolic quasilinear systems,
Wave Motion,
1,
p.
149-152, 1979.

Nonlinear Waves
173
[17]
G.
Boillat,
Chocs chamctiristiques,
C.
R.
Acad. Sc. Paris,
274A,
p.
1018-1021,1972.
[18]
G.
Boillat,
Discontinuitds de contact,
C. R. Acad. Sc. Paris,
27SA,
p.
1255-1258,1972.
[
191
G.
I.
Barenblatt,
Similarity, self-similarity and intermediate
asymptotics,
Consultant Bureau, New
York,
1979.
[20]
L.
Dresner,
Similarity solutions of nonlinear partial differential
equations,
Research Notes in Math.,
88,
Pitman,
1983.
[21]
W.
F.
Ames,
Nonlinear partial diffrential equations in engineer-
ing,
Vol.
11,
Academic Press, New
York,
1972.
[22]
L.
V. Ovsiannikov,
Group analysis of differential equations,
(En-
glish Edition, edited by
W.
F.
Ames), Academic Press, Boston,
1982.
[23]
G.
W.
Bluman and
J.
D. Cole,
Similarity methodsfor differential
equations,
Applied. Math. Sciences, Springer-Verlag,
13,
New
York,
1974.
[24]
W.
F.
Ames and A. Donato,
On the evolution of weak discon-
tinuites in
a
state chamcterized
by
invariant solutions,
Int.
J.
Non-linear Mechanics,
23,
p.
167-174, 1988.
[25]
A. Donato,
Similarity analysis and nonlinear wave propagation,
Int.
J.
Non-linear Mech.,
22,
p.
307-314, 1987.
[26]
A. Donato,
Invariant solutions and nonlinear waue propagation,
Physics
of
Earth and Planetary Interiors,
SO,
p.
52-55,
Amster-
dam,
1987.
[27]
L.
I.
Sedov,
Similarity and dimensional methods in mechanics,
Academic Press, New
York,
1959.
[28]
S.
G.
Tagare,
Evolution of discontinuity in self-similar flows,
Il
Nuovo Cimento
11B,
73-82, 1972.

174
Andrea
Donato
[29]
N. Virgopia and A. Ferraioli,
Evolution
of
weak discontinuities
waves in self-similar jiows and formation
of
secondary shocks.
The point explosion model,
J.
Appl. Math. Phys. (ZAMP),
33,
p.
63-80, 1982.
[30]
A. Donato and M.
C.
Nucci,
Similarity solutions and spherical
discontinuity waves in hyperelastic materials subjected to
a
non-
constant deformation,,
Meccanica,
23,
p.
156-159, 1988.
[31]
W.
F.
Ames, A. Donato and M.
C.
Nucci,
Analysis
of
the thread-
line equations,
Nonlinear wave motion, A. Jeffrey
ed.,
Pitman
mon.,
43,
Longman Scientific and Technical, p.
1-10, 1989.
[32]
N. Manganaro and
F.
Oliveri,
Group analysis approach in mag-
netohyddynamics:
weak
discontinuity propagation
in
a
non-
constant state,
Meccanica,
24,
p.
71-78, 1989.
[33]
M. Torrisi,
Similarity solutions and growth
of
weak
discontinu-
ities in
a
non-constant state
for
a
reactive polytropic gas,
Int.
J.
Non-linear Mech.,
24,
p.
441-449, 1989.

Integrable Nonlinear
Equations
A.S.
Fokas
Department
of
Mathematics and Computer Science
and The Institute for Nonlinear Studies
Clarkson University
Potsdam, New York
13699-5815,
U.S.A.
1
Introduction
In the last twenty years
or
so,
many physically important nonlin-
ear models have been solved exactly. Such models arise in many
branches
of
classical physics, in classical and quantum field theo-
ries, in particle physics, in relativity, in statistical physics, etc. They
take the form of ordinary differential equations, partial differential
equations, singular integrodifferential equations, operator equations,
differential-difference equations, spin systems, etc. In this article
I
will limit my discussion
to
methods
of
solution of
nonlinear evolution
equations
in
1
+
1
(i.e. one temporal and one spatial dimensions) and
in
2
+
1
(i.e.
one
temporal
and
two spatial dimensions).
Emphasis is placed on the basic ideas and on motivation. Be-
cause of economy
of
presentation, although the relevant formalism
is presented in some detail, the associated rigorous aspects are only
briefly summarized in
57.
The first, involves finding ways
of
generating large classes
of
solutions
of integrable equations, without caring about what initial
or
bound-
ary conditions these solutions satisfy. Among such methods the most
well known are:
(a)
The use
of
Lie-point symmetries
[l].
(b)
The use
of
Backlund transformations
[2].
Regarding methods
of
solution there exist two different approaches.
Nonlinear Equations in the Applied Sciences
175
Copyright
0
1992
by
Academic Press, Inc.
All
rights
of
reproduction
in
any
form
reserved.
ISBN
0-12-056752-0

176
A.
S.
Fokas
(c)
The bilinear approach of Hirota
[3].
(d)
The more general r-function approach of the Japanese School
[41.
(e)
The Dressing Method of Zakharov-Shabat
[5].
(f)
The Riemann-Hilbert direct method of Zakharov-Shabat [6], and
the
a
direct method of Zakharov and Manakov
[7].
(g)
The Direct Linearizing method of the author and Ablowitz
[8],
[
1114
131.
The second approach involves developing ways of solving initial value
problems. The most well known initial value problems solved are
regarding initial data which:
(a)
Are decaying at infinity.
(b)
Are periodic in the spatial variable
[9].
(c)
Are self similar
[lo].
The integrable nonlinear equations discussed in this article are
occasionally referred to as
soliton
equations,
or
as equations solvable
by the
Inverse Scattering Method.
It should be pointed out that there
exist certain nonlinear equations in
1
+
1
which can be linearized via
an explicit change of variables. The most well known such equation
is
the Burgers equation,
Ut
=
uxz
+
2uux.
Using the Cole-Hopf transformation,
'PX
u=-
'P'
equation
(1.1)
becomes the heat equation:
(e)
=
(fL)x
=
[F
-
(!e)2
+
(321
,
'Pt
X

Integrable Nonlinear Equations
177
or
(Pt
=
(Pxx.
Although equations like the Burgers equation share some common
features with equations solvable by the inverse scattering, the method
of solving the latter equations is far more complicated. The Inverse
Scattering Method is not based on an explicit transformation like
equation (1.2), but on
the association
of
the nonlinear equation un-
der consideration with a pair
of
linear equations known as Lax pair.
Actually one of the two equations is time independent, and can be
thought of as
a
linear eigenvalue problem.
It
is precisely this equation
which is
at
the heart of integrability.
In this article
I
will use appropriate linear eigenvalue problems
to solve several physically significant initial (and initial-boundary)
value problems. The main mathematical tools used are the
so
called
Riemann-Hilbert
(RH)
problem
[15]-[17] for equations in
1
+
1,
the
non-local Riemann-Hilbert problem
for some equations in 2
+
1
and
the
8
problem
for some equations in
2
+
1.
In $2
I
use the KPI
equation
to
illustrate the dressing method. In
$344
and
$5
I
use the
KdV, the N-wave interaction equations in
2
+
1,
and the KPII, to
illustrate the
inverse scattering transform
(IST)
method for solving
Cauchy problems with decaying initial data for equations in
1
+
1
(KdV), 2
+
1
of the nonlocal RH type (N-wave interactions), and in
2
+
1
of the
8
type (KPII).
It
is
well known that arbitrary decaying initial data for equations
in
1
+
1
will decompose in general into
a
number of solitons for large
t.
Hence solitons for equations in
1
+
1
are generic. This, together with
the fact that solitons have interesting collision properties, are the
reason why solitons have been very useful in the physical applications
of one-dimensional solvable systems. However, in multidimensions,
dispersion dominates over nonlinearity. Thus solitons “leak away”
and an arbitrary initial disturbance disperses away for large
t.
This
situation can change provided that there exists
a
mechanism to add
energy into the system.
For
DSI the boundary conditions provide
a
source of energy, and hence DSI can support localized, exponentially
decaying solutions. These solutions have several novel features not

178
A.
S.
Fokas
found in the usual solitons and have been named
dromions
by Santini
and the author. The solution
of
an initial boundary value problem
of DSI and the dromions are discussed in
$6.
A
summary of rigorous considerations and open questions regard-
ing the formal results of
$3-6
is given in
$7.
As
it was mentioned earlier, periodic and self similar problems
have also been considered for integrable equations. The periodic
problems yield to consideration of Riemann Theta functions, while
the self similar solutions yield to Painlevd equations.
A
brief intro-
duction of these results in given in
$8.
2
The Dressing Method
The dressing method introduced by Zakharov and Shabat has been
a
powerful tool for obtaining new integrable nonlinear equations as
well as characterizing large classes of solutions of these equations.
This method is applicable to both equations in
1
+
1
and in
2
+
1.
There exist several formulations of the dressing method; for
a
recent
discussion of the relationship between these formulations see
[14].
In its simplest form the dressing method starts with
a
RH
or
8
problem and then algorithmically implies:
(a)
A
Lax pair, (b)
A
nonlinear integrable equation, (c) Large classes
of
solutions of the
nonlinear equation. We illustrate this method starting with
a
nonlo-
cal
RH
problem, although the same philosophy can
be
used
for
both
local
RH
problems and
8
problems.
Consider the scalar non-local
RH
problem
P+(W,t,k)
=
JRdlP-(s,y,t,z)F(s,y,l,k,I),~
I+,+O(,,),k
pol
1
+
KJ
(2.1)
In equation
(2.1),
+(-)
denotes holomorphicity in the upper (lower)
half k-complex plane, and
JR
denotes integration over the real
axis.
We
assume that
(2.1)
has
a
unique solution. Our aim is to find
F,
the scattering data, in such
a
way that
(2.1)
can be used to generate
solutions of some nonlinear evolution equation. Let
D,,
D,, Dt
be

Integrable Nonlinear Equations
179
defined by
D,
=
8,
+
ik,
D,
=
8,
+
ik2,
Dt
=
8,
+
ik3.
(2.2)
We determine
F
by the requirement that
D,, D,, Dt
commute with
This implies
F,
=
i(l-
k)F,
F,
=
i(12
-
k2)F,
Ft
=
i(Z3
-
k3)F. (2.3)
Note that
iD,p
-
D:p
N
0(1) as
k
--$
00.
Hence
iD,p
-
Dip
-
qp,
that it must be zero. Thus
q
+
-2ipi
1)
is of
O(i)
and the unique solvability
of
(2.1)
implies
pt
=
-(pxxx
+
3ikp,,
-
3k2Px)
4-
v(px
+
ikp)
+
wp
(2.5)
or,
using
(2.4)
to eliminate
3k2p,,
The
O(k)
and
0(1)
terms
of
this equation imply
3. 3 3 3.
w
=
-tp$
-
-
49x
-
-2d;lqy.
2
2@
=
--
4
