Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


350
B.
G.
Konopelchenko
and
C.
Rogers
Now, the relation
(5.41)
yields
whence
=
~-~(p-'>z[&
-
En
+
2p-'(p-'&n-l)zz]
(5.44)
on
use
of
(5.34).
However, the relation
(5.43)
also shows
that
whence,
Accordingly,
(5.44)
shows that
I
-
~n
+
2p-'(p-'cn-1
>I=
=
0.
(5.46)
so
that the relation
(5.42)
is established and the invari-
ance
of
the Dym hierarchy
(5.28)
under the reciprocal
transformation
(5.39)
follows.
Use
of
the link between
the WKI and ZS-AKNS scattering schemes established
in the previous section may be used
to
show that this

Backlund and Reciprocal Transformations: Gauge Connections
351
invariance
of
the Dym hierarchy induces the parameter-
independent part of the auto-BT for the KdV hierarchy
Qt
=
K"qx,
n
=
1,2,
...
(5.48)
where
K
is the integro-differential operator defined by
00
(5.49)
K:=--
a2
49+29,JJ dY.
ax2
The Miura transformation
q=ux+u
2
(5.50)
between the KdV hierarchy given by (5.42), (5.43) and
the mKdV hierarchy
ut
=
MnuX,
n
=
1,2,
...
(5.51)
where
00
M:=--
a2
4u2+4uXl dyu (5.52)
also emerges naturally via the linking process. The de-
tails are given in
[29].
Recently, systems analogous to the Dym hierarchy
have been introduced which are related to the Caudrey-
Dodd-Gibbon
(CDG)
and Kaup
-
Kupershmidt
(KK)
hi-
erarchies in the same way that the Dym hierarchy
is
re-
lated to the mKdV and KdV hierarchies. Explicit auto-
BTs for the
CDG
and
KK
hierarchies may be generated
via reciprocal invariance. The details are given in [30].
8x2

352
B.
G.
Konopelchenko
and
C.
Rogers
7
Reciprocal Transformations in
2
+
I-
Dimensions. Application to
the
Kadomtsev-
Petviashvili Equation.
The notion of reciprocal transformations in
2
+
l-dimen-
sions was introduced in
[31].
Here it
is
shown that the
integrable generalization of the Dym equation to
2
+
1-
dimensions as given by Konopelchenko and Dubrovsky in
[32]
is linked by such
a
reciprocal transformation to the
singularity manifold equation associa.ted with application
of
the Painlev6 test to the Kadomtsev-Petviashvili (KP)
equation
[33].
This result is used to generate
a
novel
involutory invariance of the
2
+
I-dimensional Dym equa-
tion. The following extensions to
2
+
l-dimensions of the
reciprocal result
RI
is used in the sequel
[31].
RI
I
The integro-differential equation
is taken under the reciprocal traasformation
dx’
=
Tdx
-
Fdt
+
a,’T,
dy,
y’=y,
t=t
I
1
RII
0
<(
T
I<
00
to the associated equation
I
(7.2)

Backlund and Reciprocal Transformations: Gauge Connections
353
where
and
D:
:=
ax
=
(l/T’)<,
In addition,
T’
is the multiplicative operator defined by
T”$
:=
T’d
(7.8)
The above result is readily established along the lines
of
RI
f311.
We
iext
turn
to
the
Lax
system with operators
[32]
.L
=
a:
+
QU(Z,
y,
tpx
+
Pu(q
y,
t)
+
ay,
-
3pux
-
,apu’
3
+
3pa;’uy
+
a,

354
B.
G.
Konopelchenko
and
C.
Rogers
The commutativity condition
[L,T]
=
0
(7.10)
produces the class
of
nonlinear evolution equations in
2
+
1-dimensions
The specialisation
a
=
0
produces
a
Kadomtsev-Petviash-
vili equation, while
,B
=
0
yields
a
modified Kadomtsev-
Petviashvili equation
[32].
If
we set
a
=
0,P
=
1/6
together with
x*
=
x,y*
=
y/&,
t*
=
-t
then the
KP
equation is obtained in the form
considered by Weiss
[34],
namely
uy*y*
+
(Ut*
+
uu,*
+
Ux*x*x*)x*
=
0
.
(7.12)
On the other hand, if we take
[32]
L
=
r2(x,
Y,t)a:
+
a,,
(7.13)
T
=
4r3a:
+
[6r2r,
-
6r2a,'(r,/r2)]a:
-
at,
then the commutativity condition
(7.10)
produces
a
gen-
eralization
of
the Dym equation to
2
+
1-dimensions, viz
3 -1
2
-1
rt
=
7-
r,,,
+
3r
[r
a,
(r,/r2)>1,.
(7.14)
It will now be shown that the latter equation is linked by
a
2
+
I-dimensional reciprocal transformation to the sin-
gularity manifold equation associated with the
KP
equa-
tion.

Backlund and Reciprocal Transformations: Gauge Connections
355
Thus, the
2
+
I-dimensional Dym equation
(7.14)
may
be re-written in the
form
pt
+EX
=
0,
(7.15)
where
p
=
r-l
and
(7.16)
2 -1
6
=
a,"P-'(P-l)xxx
-
3P3(P-
a3:
py)y].
Under the reciprocal transformation
R
(7.17)
dZ
=
pdx-6
dt
+
i9F1py
dy,
y=y,
t=t
-
1
p=-
P
0
<I
P
I<
-
we
obtain
pt
+
ci?
=
0,
where
with
E
=
El
+
E2
(7.18)
(7.19)

356
B.
G.
Konopelchenko
and
C.
Rogers
But,
-
--
VPY
XPY-
so
that
E2
=
3pa;l[-(l/p)(a;
1-
pg)
2
(1/p)z
-
(l/p)a,'pyy].
Thus, the reciprocal associate under
R
of
the
2+
l-dimen-
sional Dym equation
is
If
we
now
introduce the potential
4
according to
-
p=+-
x
-
2%
then
(7.20)
yields
where
(7.21)
=
0
(7.22)
(7.23)
denotes the Schwarzian derivative
of
4.

Backlund and Reciprocal Transformations: Gauge Connections
357
Under the change
of
variables
(7.22) produces the singularity manifold equation
+
{&x*}
+
-
1
(--)2)
$3,.
=
0
(7.25)
2
$I*
associated with the
KP
equation
[34].
The link to the
latter is obtained via the relation
.
(7.26)
u
=
--
-
$X*
dX*
Combination of the invariance
of
the singularity
man-
ifold equation (7.25) under the Mobius transformation
M:
$
k
=-
ad-bcfO
c$
+
d'
(7.27)
and the association
of
the
2
+
I-dimension of the
2
+
1-
dimensional Dym equation (7.15) with (7.22) under the
reciprocal transformation
x
=
871-
p
=
$3,
y
=y,
t =t,
p
=
1/p,
z
=
a,-'p=
4,
-
(7.28)
induces
a
novel invariance of the
2
+
1-dimensional Dym
equation
as
indicated
in
Figure 5.
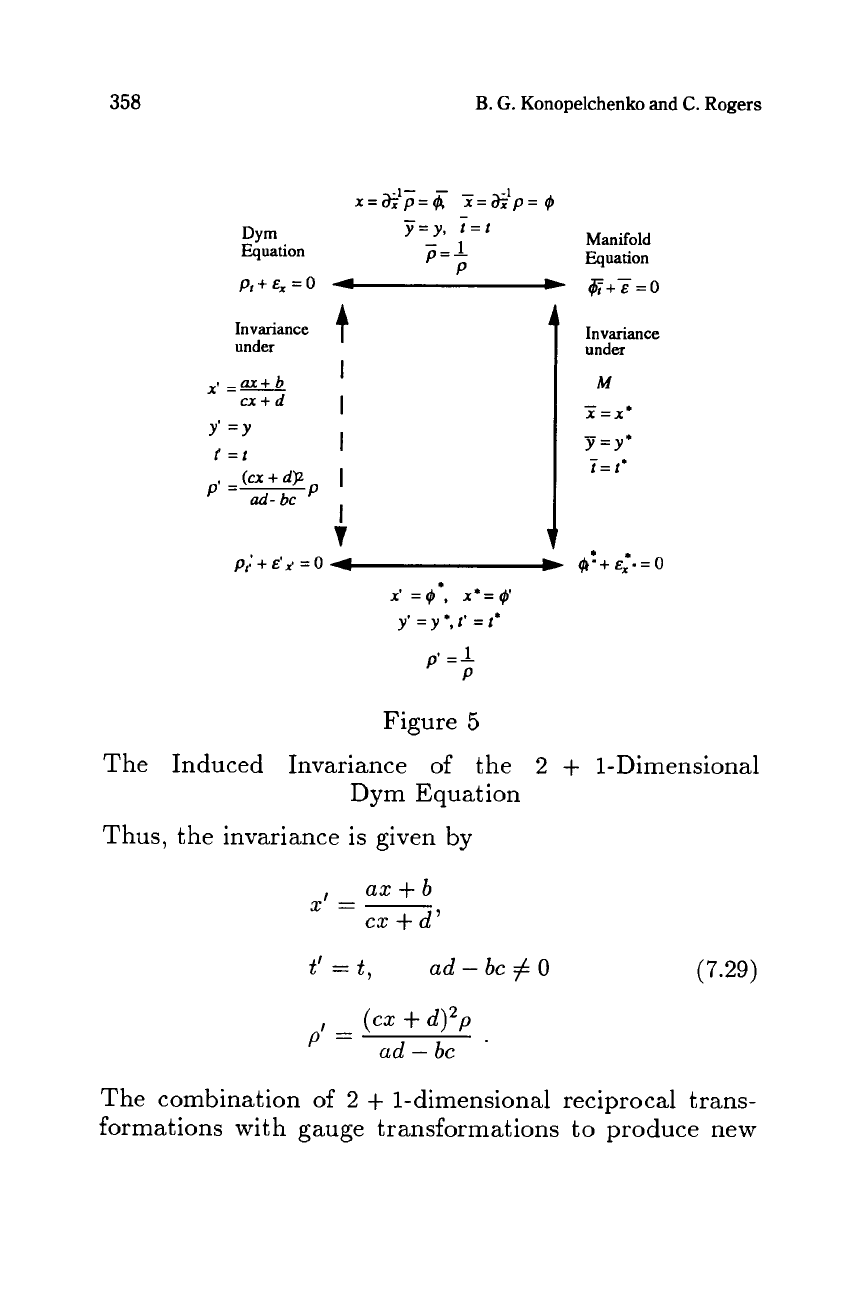
358
h
Invariance
t
under
I
cx+d
I
I
I
-m+b
Y'
=Y
(cx
+
dP
I
P
p'
=-
t=t
ad-
bc
B.
G.
Konopelchenko
and
C.
Rogers
Invariance
under
M
x
=x*
Y
=Y*
i=
I*
-
-
Figure
5
The Induced Invariance
of
the
2
+
1-Dimensional
Dym Equation
Thus, the invariance is given by
ad
-
bc
#
0
I
t =t,
(7.29)
The combination
of
2
+
1-dimensional reciprocal trans-
formations with gauge transformations
to
produce new

Backlund
and
Reciprocal Transformations: Gauge Connections
359
integrable systems in
a
manner analogous to that of Sec-
tion
5
for
1
+
I-dimensional systems is suggested. Indeed,
gauge transformations have been recently used in
2
+
1-
dimensions by Konopelchenko and Matkarimov [35] to
link two nonlinear integrable systems of importance,
namely, the Ishimori system [36]
St(w,t)
+
s
x
(%z
+
Q2S,,)
+
43,
+
4ysz
=
0,
(7.30)
Q2
=
fl
with the Davey-Stewartson system. The Ishimori system
represents the
2
+
1-dimensional integrable extension
of
the continuous Heisenber ferromagnet model in
1
+
1-
dimensions, namely [37,38
7
st
+
s
x
s,,
=
0,
(7.31)
s.s
=
1
In [27, 281, (7.31) has been linked by
a
combination of
gauge and reciprocal transformations to the Shimuzi-
Wadati equation [39]
qt
f
WJG-i-g)ZZ
=
0
(7.32)
An analogous procedure is available in
2
+
1-dimensions
to construct an integrable 2+1-dimensional version
of
the
Shimuzi- Wadati equation.
To
conclude, it is noted that reciprocal transforma-
tions may also be employed in soliton theory to analyse
the distinctive symmetry structure of interconnected in-
tegrable nonlinear hierarchies
[40].
Acknowledgements
Support under
-
Natural Sciences of Ca.nada Grant. No.
A0879 is gratefully acknowledged
(C.R.)
