Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


340
B.
G.
Konopelchenko
and
C.
Rogers
where
exp{2i(A?
+
A;
-
p2
-
v2)t
(4.21)
and C1(p),
C2(v)
are arbitrary functions.
The presence of arbitrary functions in the solutions
Pn1
,O
and
Po,n,
and, hence, in the solutions
Pn,,n,
is the
important feature
of
the 2+1-dimensional case. It leads to
a
much richer class
of
solutions than
in
the one-dimen-
sional case. In particular, an appropriate choice of the
functions
Cik)
and
Cik)
in the
Pn,,n2
gives rise to solutions
of
the
DS
equation which are exponentially localized in
the plane
[lo].
The simplest solution of this type is the
breather
+
JZcosh{(A
-
p)(x
-
v1t)
-
(A
+
P)(Y
-
v2t)
+
q.
(4.23)
The recent discovery of these
2
+
1-dimensional localized
structures via BTs has injected
a
new interest into the
study
of
higher-dimensional integrable systems. In par-
ticular, it has led to
a
study of certain boundary value
problems for the
DS
equation and
of
2
+
1-dimensional
coherent entities which have been termed
dromions
[22].

EJiicklund and Reciprocal Transformations: Gauge Connections
341
5
Reciprocal Transformations in
1
+
1-
Dimensions Linked Inverse Scattering
Schemes.
Reciprocal transformations have been extensively em-
ployed in Continuum Mechanics not only to reveal hid-
den symmetries in nonlinear systems but also to solve
nonlinear boundary value problems. These applications
are described in detail in Rogers and Shadwick
[l]
and
Rogers and Ames
[23].
In the present context of Soliton Theory, reciprocal
transformations in
1
+
I-dimensions may
be
shown to be
a
key component in the link between the
AKNS
and
WKI
inverse scattering schemes
[24].
Moreover, the Dym hier-
archy
as
set forth
by
Calogero and Degasperis
[17]
is in-
variant under
a
class of reciprocal transformations. This
result may be used
to
construct
a
generic auto-BT for
the
KdV
hierarchy in
a
novel manner.
It is this area
of
application
of
reciprocal transformations that
we
now
describe.
In the sequel,
we
make use of the following result
[25]:
RI
The conservation law
d
{T
(---
ad
:
u)}
+
2
{F
(--
ad
:
u)}
=
0
(5.1)
at
ax
'
at
dX
6%'
dt
is transformed to the associated conservation law
2-
{TI
(---
aa
:
.>)
+d
{F'
(---
aa
:
u)}
=
0
at
I
ax'
'
at'
dX'
dz'
'
at'

342
B.
G.
Konopelchenko
and
C.
Rogers
by the
reciprocal
transformation
R
(5-3)
dx'
=
Tdx
-
Fdt,
1
T(D;
3';
u)
'
T'
=
-F(D;
d
:
U)
F'
=
T(D;
d
:
U)
where
d
F'd
d
a:=
-
=
--+-
dt
T'
ax' dt"
0
<I
T
I<
00.
The above result is readily demonstrated.
implies that
Thus,
(5.3)
dX'
at
whence compatibility yields
(5.1).
Similarly,
(5.3)
implies that
-
=
-F
ax'
dX
--
-
T,
dx
F
dx
1
ax'
T' dt'
T
-=-
-
-
--
and compatibility gives
(5.2).
tion
R
is
reciprocal.
It
is
readily shown that
R2
=
I
so
that the transforma-
Thus,
dx"
=
T'
dx'
-
F'
dt'
=
T'(T
dx
-
F
dt)
-
F'
dt'
=
dx,
dt"
=
dt'
=
dt,

Backlund and Reciprocal Transformations: Gauge Connections
343
The above result will now be shown to be
a
key compo-
nent in the link between the
ZS-AKNS
scattering scheme
and the WKI scattering scheme
}
$x*
=
U*$,
$t*
=
V*$,
(5.4)
where
-ix*
x*q*
.
(5.5),
(5.6)
In this connection,
we
recall the result
of
Section
3
con-
cerning the gauge transformation
G
of the ZS-AKNS
scheme
(3.8)
-
(3.11).
In particular,
we
consider the
gauge transformation
G
=
g-l
given by
0
=
g-lug
-
g-lgz,
g-1
(5.7)
?I,
=
s-v,
v
=
g-lvg
-
g-lgt
I
where, as in Zakharov and Takhtadzhyan
[as],
g
is
taken
as
the solution
of
the system
(3.8)
-
(3.11)
with
X
=
0
so
that

344
B.
G.
Konopelchenko
and
C.
Rogers
It is observed that the gauge transformation
g-I
has in-
verse
g
with
4
=
g4,
v
=
gVg-l
+
gtg-I,
U=gW+gxg
(5.10)
whence, with the choice of
g
given by
(5.8)-(5.9),
the
inverse scattering scheme
with
where
with
0
=
AS,
s=g-l(l
0
-1
o)g=(:
:a)
a2
+
bc
=
1
(5.11)
(5.12)
(5.13)
(5.14)
(5.15)
is obtained. The inverse scattering scheme
(5.11)
gauge
equivalent to the
ZS-AKNS
scheme
(3.8)-(3.11)
has
compatibility condition
St
-
A-Vz
+
SP
-
vs
=
0,
(5.16)

Bicklund and Reciprocal Transformations: Gauge Connections
345
where is given by
(5.13).
inverse scattering scheme
(5.11).
We next apply a reciprocal transformation
R
to the
Thus, if
(5.16)
delivers the conservation law
at
+
eZ
=
0
(5.17)
then introduction
of
x*,t*
according to
dx*
=
adz
-
edt,
t*
=
t
)
R
(5.18)
leads
to
the reciprocally associated inverse scattering
scheme
(5.19)
&*
=
u*?J
&*
=
V*Tj
where
€0
v*=v+-.
0
u*
=
-.
a
a
(5.20), (5.21)
If,
following the work
of
Ishimori
[27],
Wadati and
Sogo
[28]
we impose the further transformation
r*=
JpTq
-ic
I
with inverse
iq*
}
T-'
b=
dm
c=
d-
ir*
(5.22)
(5.23)
346
B.
G.
Konopelchenko
and
C.
Rogers
G
L
ZS-AKNS
v
Scheme
1
-
then the inverse scattering scheme
(5.19)
is taken to the
WKI
system
(5.4)
with
?,b
-,
4
and
X
=
-X*i.
the ZS-AKNS inverse scattering scheme is linked to the
WKI scheme may be decomposed according the the fol-
lowing diagram:
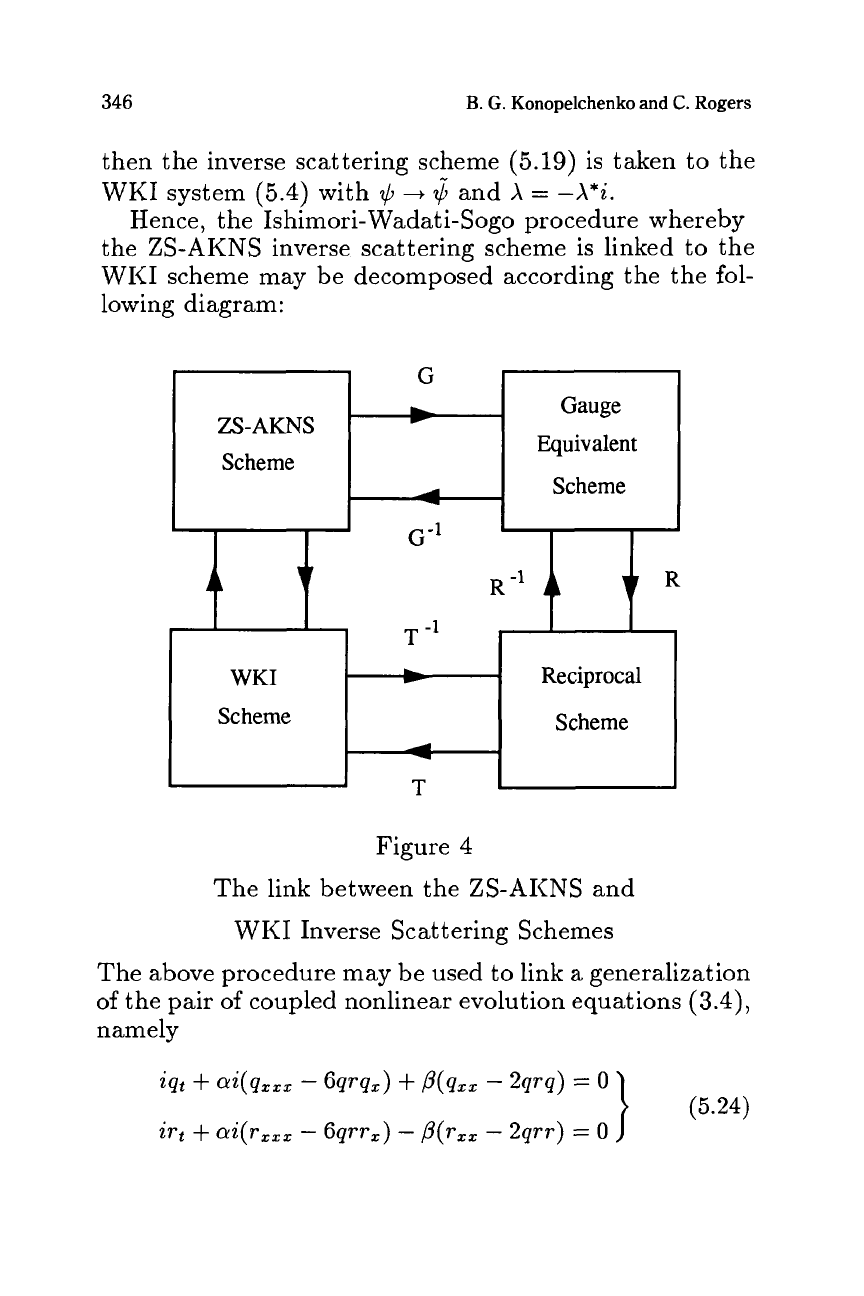
Hence, the Ishimori-Wadati-Sogo procedure whereby
Gauge
Equivalent
Scheme
Ir.
v
Figure
4
The link between the ZS-AKNS and
WKI
Inverse Scattering Schemes
The above procedure may be used to link
a
generalization
of
the pair
of
coupled nonlinear evolution equations
(3.4),
namely
R
WKI
Scheme
L
-
Reciprocal
Scheme
1
-
T

Backlund and Reciprocal Transformations: Gauge Connections
347
of
the ZS-AKNS system with the coupled nonlinear pair
of
the WKI system (see Ishimori
[27]).
In particular, the
specializations
r
=
r*
=
-I,&
=
-1,p
=
O
together with
the substitution
p2
=
1
+
q*
in
(5.25)
produces the link
between the KdV equation
and the Dym equation
(p”t
+
2(p-l)zzz
=
0.
(5.27)
G
Reciprocal Invariance
of
the
Dym
Hierarchy
Here, we consider the Dym hierarchy
[9]
pt
=
,~-~(-D~rIr}~pp,,
n
=
1,2,
...
(5.28)
where the operators
D
and
I
are defined by
while
r
denotes the multiplicative operator given by
r#(x,
t)
:=
r#(x,
t)
(5.31)

348
B.
G.
Konopelchenko
and
C.
Rogers
where
r
=
p-l
#
0.
It is assumed that
1
-
p
and
1
-
T
are
bona
fide
potentials
[9].
In particular, it is required that
lim
p
=
1.
z+fm
The hierarchy
(5.28)
may be re-written as
Pt
+
En,x
=
0,
n
=
1,2,
...
(5.32)
where
(5.33)
and the
flux
terms
cn
are generated iteratively by the
relations
00
En
=
-
1
P-l[P-1&,-11zzz
dx,
n=1,2
,...,
EO=O.
(5.34)
Thus,
(5.32)
together with
(5.34)
yields
It
is noted that the base equation
of
the nonlinear hier-
archy
(5.35)
corresponding to
n
=
1
is the Dym equation
(5.27).
Now,
the reciprocal theorem RI shown that
du
d
-
+
-A(D(O)~,
D(%,
.
.
.
,
D(~)~)
=
o
at
dx
(5.36)
is taken to
U'
U' U'
(D
:=
$A)
(5.37)

Backlund and Reciprocal Transformations: Gauge Connections
349
under the reciprocal transformation
dx’
=
udx-A
D(O)u, D(’)u,.
. .
,
D(n)~
1
UI
=
-
U’
O<IUI<Oo.
(
(5.38)
Accordingly, under the reciprocal transformat ion
1
dx’
=
p2dx-2 dt, dt’
=
dt,
1
-,
P
O<IpI<m.
the hierarchy
(5.35)
becomes
R’
(5.39)
i
n
=
1,2,.
. . .
(5.40)
The invariance of the Dym equation under the reciprocal
transformation
(5.39)
in the case
n
=
1
was established
in
[24].
The general result was established in
[29].
In
order to prove the result for the hierarchy, it is required
to show that if we introduce
EL
n
=
1,2,.
.
.
,
accordingly
to
(5.41)
1-1
I
(P
En)z
+
(P-l€n)z
=
0,
n
=
1,2,
...,
then
00
n
=
1,2,.
.
. . (5.42)
