Anderson D.R., Sweeney D.J., Williams T.A. Essentials of Statistics for Business and Economics

8.2 Population Mean: σ Unknown 315

of error is then given by t

α/2

. With this margin of error, the general expression for an

interval estimate of a population mean when σ is unknown follows.

s兾

兹

n

The reason the number of degrees of freedom associated with the t value in expression

(8.2) is n ⫺ 1 concerns the use of s as an estimate of the population standard deviation σ.

The expression for the sample standard deviation is

Degrees of freedom refer to the number of independent pieces of information that go into the

computation of 兺(x

i

⫺ )

2

. The n pieces of information involved in computing 兺(x

i

⫺ )

2

are as follows: x

1

⫺ , x

2

⫺ ,..., x

n

⫺ . In Section 3.2 we indicated that 兺(x

i

⫺ ) ⫽ 0

for any data set. Thus, only n ⫺ 1 of the x

i

⫺ values are independent; that is, if we know

n ⫺ 1 of the values, the remaining value can be determined exactly by using the condition

that the sum of the x

i

⫺ values must be 0. Thus, n ⫺ 1 is the number of degrees of freedom

associated with 兺(x

i

⫺ )

2

and hence the number of degrees of freedom for the t distribution

in expression (8.2).

To illustrate the interval estimation procedure for the σ unknown case, we will consider

a study designed to estimate the mean credit card debt for the population of U.S. households.

A sample of n ⫽ 70 households provided the credit card balances shown in Table 8.3. For

this situation, no previous estimate of the population standard deviation σ is available. Thus,

the sample data must be used to estimate both the population mean and the population stan-

dard deviation. Using the data in Table 8.3, we compute the sample mean ⫽ $9312 and the

sample standard deviation s ⫽ $4007. With 95% confidence and n ⫺ 1 ⫽ 69 degrees of

x¯

x¯x¯x¯x¯

x¯x¯

s ⫽

冑

兺(x

i

⫺ x¯)

2

n ⫺ 1

INTERVAL ESTIMATE OF A POPULATION MEAN: σ UNKNOWN

(8.2)

where s is the sample standard deviation, (1 ⫺ α) is the confidence coefficient, and

t

α/2

is the t value providing an area of α/2 in the upper tail of the t distribution with

n ⫺ 1 degrees of freedom.

x¯

⫾

t

α/2

s

兹

n

TABLE 8.3 CREDIT CARD BALANCES FOR A SAMPLE OF 70 HOUSEHOLDS ($)

9430

7535

4078

5604

5179

4416

10676

1627

10112

6567

13627

18719

14661

12195

10544

13659

7061

6245

13021

9719

2200

10746

12744

5742

7159

8137

9467

12595

7917

11346

12806

4972

11356

7117

9465

19263

9071

3603

16804

13479

14044

6817

6845

10493

615

13627

12557

6232

9691

11448

8279

5649

11298

4353

3467

6191

12851

5337

8372

7445

11032

6525

5239

6195

12584

15415

15917

12591

9743

10324

file

W

EB

NewBalance

CH008.qxd 8/16/10 6:38 PM Page 315

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).

Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

316 Chapter 8 Interval Estimation

freedom, Table 8.2 can be used to obtain the appropriate value for t

.025

. We want the tvalue

in the row with 69 degrees of freedom, and the column corresponding to .025 in the upper

tail. The value shown is t

.025

⫽ 1.995.

We use expression (8.2) to compute an interval estimate of the population mean credit

card balance.

The point estimate of the population mean is $9312, the margin of error is $955, and the

95% confidence interval is 9312 ⫺ 955 ⫽ $8357 to 9312 ⫹ 955 ⫽ $10,267. Thus, we are

95% confident that the mean credit card balance for the population of all households is

between $8357 and $10,267.

The procedures used by Minitab, Excel, and StatTools to develop confidence intervals

for a population mean are described in Appendixes 8.1, 8.2, and 8.3. For the household

credit card balances study, the results of the Minitab interval estimation procedure are

shown in Figure 8.6. The sample of 70 households provides a sample mean credit card bal-

ance of $9312, a sample standard deviation of $4007, a standard error of the mean of $479,

and a 95% confidence interval of $8357 to $10,267.

Practical Advice

If the population follows a normal distribution, the confidence interval provided by ex-

pression (8.2) is exact and can be used for any sample size. If the population does not fol-

low a normal distribution, the confidence interval provided by expression (8.2) will be

approximate. In this case, the quality of the approximation depends on both the distribution

of the population and the sample size.

In most applications, a sample size of n ⱖ 30 is adequate when using expression (8.2)

to develop an interval estimate of a population mean. However, if the population distribu-

tion is highly skewed or contains outliers, most statisticians would recommend increasing

the sample size to 50 or more. If the population is not normally distributed but is roughly

symmetric, sample sizes as small as 15 can be expected to provide good approximate con-

fidence intervals. With smaller sample sizes, expression (8.2) should be used only if the

analyst believes, or is willing to assume, that the population distribution is at least approxi-

mately normal.

Using a Small Sample

In the following example we develop an interval estimate for a population mean when the

sample size is small. As we already noted, an understanding of the distribution of the popu-

lation becomes a factor in deciding whether the interval estimation procedure provides

acceptable results.

Scheer Industries is considering a new computer-assisted program to train maintenance

employees to do machine repairs. In order to fully evaluate the program, the director of

9312

⫾

955

9312

⫾

1.995

4007

兹

70

Larger sample sizes are

needed if the distribution of

the population is highly

skewed or includes outliers.

Variable N Mean StDev SE Mean 95% CI

NewBalance 70 9312 4007 479 (8357, 10267)

FIGURE 8.6 MINITAB CONFIDENCE INTERVALFOR THE CREDITCARD BALANCE SURVEY

CH008.qxd 8/16/10 6:38 PM Page 316

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).

Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

8.2 Population Mean: σ Unknown 317

manufacturing requested an estimate of the population mean time required for maintenance

employees to complete the computer-assisted training.

A sample of 20 employees is selected, with each employee in the sample completing

the training program. Data on the training time in days for the 20 employees are shown in

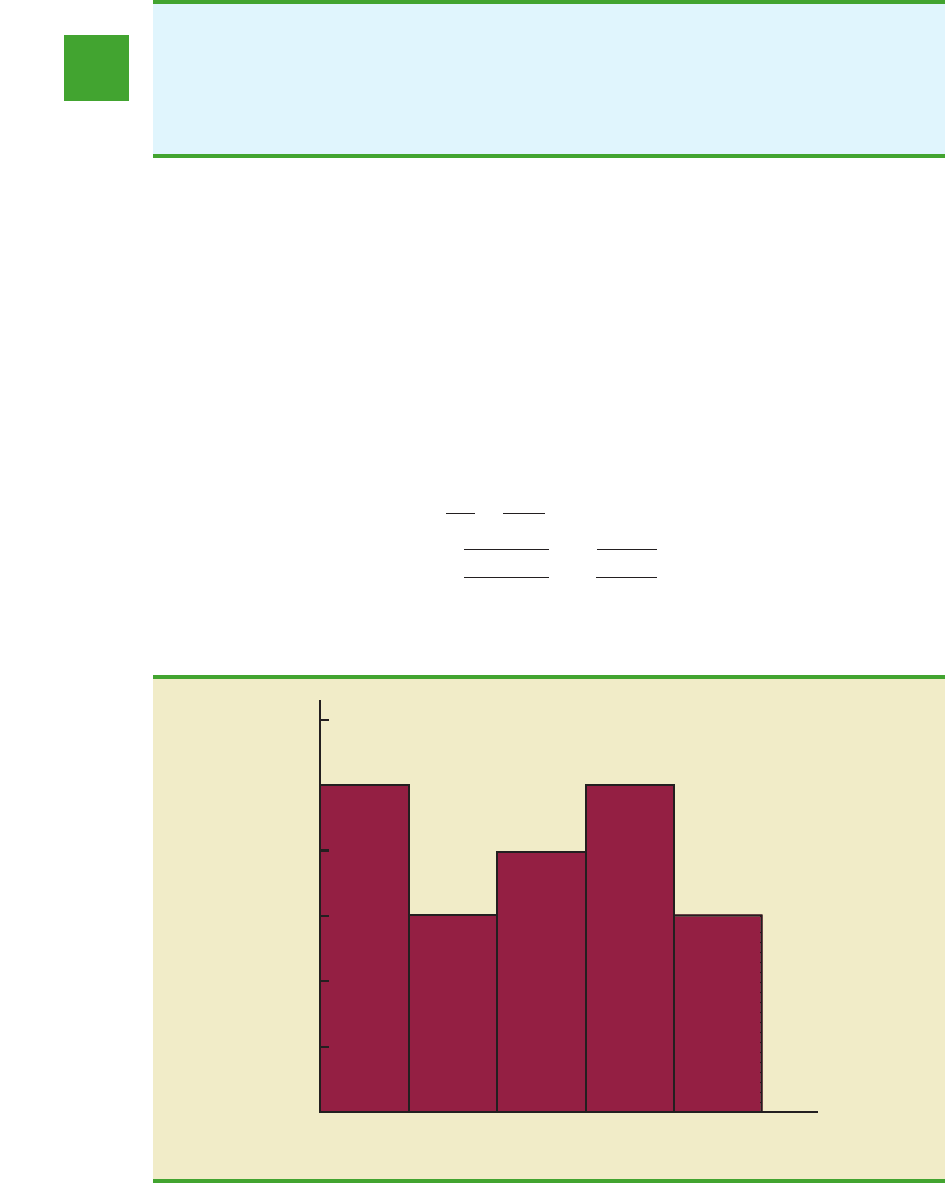
Table 8.4. Ahistogram of the sample data appears in Figure 8.7. What can we say about the

distribution of the population based on this histogram? First, the sample data do not sup-

port the conclusion that the distribution of the population is normal, yet we do not see any

evidence of skewness or outliers. Therefore, using the guidelines in the previous subsection,

we conclude that an interval estimate based on the t distribution appears acceptable for the

sample of 20 employees.

We continue by computing the sample mean and sample standard deviation as follows.

s ⫽

冑

兺(x

i

⫺ x¯)

2

n ⫺ 1

⫽

冑

889

20 ⫺ 1

⫽ 6.84 days

x¯ ⫽

兺x

i

n

⫽

1030

20

⫽ 51.5 days

52 59 54 42

44 50 42 48

55 54 60 55

44 62 62 57

45 46 43 56

TABLE 8.4

TRAINING TIME IN DAYS FOR A SAMPLE OF 20 SCHEER

INDUSTRIES EMPLOYEES

5

4

3

2

1

0

Frequency

Training Time (days)

40

45 50 55 60 65

6

FIGURE 8.7 HISTOGRAM OF TRAINING TIMES FOR THE SCHEER INDUSTRIES SAMPLE

file

WEB

Scheer

CH008.qxd 8/16/10 6:38 PM Page 317

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).

Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

318 Chapter 8 Interval Estimation

For a 95% confidence interval, we use Table 2 of Appendix B and n ⫺ 1 ⫽ 19 degrees of

freedom to obtain t

.025

⫽ 2.093. Expression (8.2) provides the interval estimate of the pop-

ulation mean.

The point estimate of the population mean is 51.5 days. The margin of error is 3.2 days and

the 95% confidence interval is 51.5 ⫺ 3.2 ⫽ 48.3 days to 51.5 ⫹ 3.2 ⫽ 54.7 days.

Using a histogram of the sample data to learn about the distribution of a population is

not always conclusive, but in many cases it provides the only information available. The

histogram, along with judgment on the part of the analyst, can often be used to decide

whether expression (8.2) can be used to develop the interval estimate.

Summary of Interval Estimation Procedures

We provided two approaches to developing an interval estimate of a population mean. For

the σ known case, σ and the standard normal distribution are used in expression (8.1) to

compute the margin of error and to develop the interval estimate. For the σ unknown case,

the sample standard deviation s and the t distribution are used in expression (8.2) to com-

pute the margin of error and to develop the interval estimate.

A summary of the interval estimation procedures for the two cases is shown in

Figure 8.8. In most applications, a sample size of n ⱖ 30 is adequate. If the population has

a normal or approximately normal distribution, however, smaller sample sizes may be used.

51.5

⫾

3.2

51.5

⫾

2.093

冢

6.84

兹

20

冣

Can the population

standard deviation

be assumed known?

Use the sample

standard deviation

s to estimate

Use

±

n

x

z

α

/2

Use

±

n

x

t

s

α

/2

Yes No

σ

Known Case

σ

Unknown Case

FIGURE 8.8 SUMMARY OF INTERVAL ESTIMATION PROCEDURES

FOR A POPULATION MEAN

CH008.qxd 8/16/10 6:38 PM Page 318

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).

Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

8.2 Population Mean: σ Unknown 319

test

SELF

Exercises

Methods

11. For a t distribution with 16 degrees of freedom, find the area, or probability, in each region.

a. To the right of 2.120

b. To the left of 1.337

c. To the left of ⫺1.746

d. To the right of 2.583

e. Between ⫺2.120 and 2.120

f. Between ⫺1.746 and 1.746

12. Find the t value(s) for each of the following cases.

a. Upper tail area of .025 with 12 degrees of freedom

b. Lower tail area of .05 with 50 degrees of freedom

c. Upper tail area of .01 with 30 degrees of freedom

d. Where 90% of the area falls between these two t values with 25 degrees of freedom

e. Where 95% of the area falls between these two t values with 45 degrees of freedom

13. The following sample data are from a normal population: 10, 8, 12, 15, 13, 11, 6, 5.

a. What is the point estimate of the population mean?

b. What is the point estimate of the population standard deviation?

c. With 95% confidence, what is the margin of error for the estimation of the population

mean?

d. What is the 95% confidence interval for the population mean?

14. A simple random sample with n ⫽ 54 provided a sample mean of 22.5 and a sample stan-

dard deviation of 4.4.

a. Develop a 90% confidence interval for the population mean.

b. Develop a 95% confidence interval for the population mean.

For the σ unknown case, a sample size of n ⱖ 50 is recommended if the population dis-

tribution is believed to be highly skewed or has outliers.

NOTES AND COMMENTS

1. When σ is known, the margin of error, z

α/2

(),

is fixed and is the same for all samples of

size n. When σ is unknown, the margin of error,

t

α/2

( ), varies from sample to sample. This

variation occurs because the sample standard

deviation s varies depending upon the sample

selected. A large value for s provides a larger

margin of error, while a small value for s pro-

vides a smaller margin of error.

2. What happens to confidence interval estimates

when the population is skewed? Consider a

population that is skewed to the right with large

data values stretching the distribution to the

right. When such skewness exists, the sample

mean and the sample standard deviation s are

positively correlated. Larger values of s tend to

x¯

s兾

兹

n

σ兾

兹

n

be associated with larger values of . Thus,

when is larger than the population mean, s

tends to be larger than σ. This skewness causes

the margin of error, t

α/2

( ), to be larger than

it would be with σ known. The confidence in-

terval with the larger margin of error tends to

include the population mean μ more often than

it would if the true value of σ were used. But

when is smaller than the population mean, the

correlation between and s causes the margin

of error to be small. In this case, the confidence

interval with the smaller margin of error tends

to miss the population mean more than it would

if we knew σ and used it. For this reason, we

recommend using larger sample sizes with

highly skewed population distributions.

x¯

s兾

兹

n

x¯

CH008.qxd 8/16/10 6:38 PM Page 319

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).

Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

320 Chapter 8 Interval Estimation

c. Develop a 99% confidence interval for the population mean.

d. What happens to the margin of error and the confidence interval as the confidence

level is increased?

Applications

15. Sales personnel for Skillings Distributors submit weekly reports listing the customer con-

tacts made during the week. Asample of 65 weekly reports showed a sample mean of 19.5

customer contacts per week. The sample standard deviation was 5.2. Provide 90% and 95%

confidence intervals for the population mean number of weekly customer contacts for the

sales personnel.

16. The mean number of hours of flying time for pilots at Continental Airlines is 49 hours per

month (The Wall Street Journal, February 25, 2003). Assume that this mean was based on

actual flying times for a sample of 100 Continental pilots and that the sample standard

deviation was 8.5 hours.

a. At 95% confidence, what is the margin of error?

b. What is the 95% confidence interval estimate of the population mean flying time for

the pilots?

c. The mean number of hours of flying time for pilots at United Airlines is 36 hours

per month. Use your results from part (b) to discuss differences between the flying

times for the pilots at the two airlines. The Wall Street Journal reported United Air-

lines as having the highest labor cost among all airlines. Does the information in

this exercise provide insight as to why United Airlines might expect higher labor

costs?

17. The International Air Transport Association surveys business travelers to develop quality

ratings for transatlantic gateway airports. The maximum possible rating is 10. Suppose a

simple random sample of 50 business travelers is selected and each traveler is asked to pro-

vide a rating for the Miami International Airport. The ratings obtained from the sample of

50 business travelers follow.

6 4 6 8 7 7 6 3 3 8 10 4 8

7 8 7 5 9 5 8 4 3 8 5 5 4

4 4 8 4 5 6 2 5 9 9 8 4 8

9 9 5 9 7 8 3 10 8 9 6

Develop a 95% confidence interval estimate of the population mean rating for Miami.

18. Older people often have a hard time finding work. AARPreported on the number of weeks

it takes a worker aged 55 plus to find a job. The data on number of weeks spent searching

for a job contained in the file JobSearch are consistent with the AARP findings (AARP

Bulletin, April 2008).

a. Provide a point estimate of the population mean number of weeks it takes a worker aged

55 plus to find a job.

b. At 95% confidence, what is the margin of error?

c. What is the 95% confidence interval estimate of the mean?

d. Discuss the degree of skewness found in the sample data. What suggestion would you

make for a repeat of this study?

19. The average cost per night of a hotel room in New York City is $273(SmartMoney, March

2009).Assumethis estimate is based on a sample of 45 hotels and that the sample standard

deviation is $65.

a. With 95% confidence, what is the margin of error?

b. What is the 95% confidence interval estimate of the population mean?

c. Two years ago the average cost of a hotel room in New York City was $229. Discuss

the change in cost over the two-year period.

test

SELF

file

WEB

Miami

file

WEB

JobSearch

CH008.qxd 8/16/10 6:38 PM Page 320

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).

Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

8.3 Determining the Sample Size 321

20. Is your favorite TV program often interrupted by advertising? CNBC presented statistics

on the average number of programming minutes in a half-hour sitcom (CNBC, February

23, 2006). The following data (in minutes) are representative of its findings.

21.06 22.24 20.62

21.66 21.23 23.86

23.82 20.30 21.52

21.52 21.91 23.14

20.02 22.20 21.20

22.37 22.19 22.34

23.36 23.44

Assume the population is approximately normal. Provide a point estimate and a 95% con-

fidence interval for the mean number of programming minutes during a half-hour televi-

sion sitcom.

21. Consumption of alcoholic beverages by young women of drinking age has been increas-

ing in the United Kingdom, the United States, and Europe (The Wall Street Journal, Feb-

ruary 15, 2006). Data (annual consumption in liters) consistent with the findings reported

in The Wall Street Journal article are shown for a sample of 20 European young women.

266 82 199 174 97

170 222 115 130 169

164 102 113 171 0

93 0 93 110 130

Assuming the population is roughly symmetric, construct a 95% confidence interval for

the mean annual consumption of alcoholic beverages by European young women.

22. Disney’s Hannah Montana: The Movie opened on Easter weekend in April 2009. Over the

three-day weekend, the movie became the number-one box office attraction (The Wall

Street Journal, April 13, 2009). The ticket sales revenue in dollars for a sample of 25

theaters is as follows.

20,200 10,150 13,000 11,320 9,700

8,350 7,300 14,000 9,940 11,200

10,750 6,240 12,700 7,430 13,500

13,900 4,200 6,750 6,700 9,330

13,185 9,200 21,400 11,380 10,800

a. What is the 95% confidence interval estimate for the mean ticket sales revenue per

theater? Interpret this result.

b. Using the movie ticket price of $7.16 per ticket, what is the estimate of the mean num-

ber of customers per theater?

c. The movie was shown in 3118 theaters. Estimate the total number of customers who

saw Hannah Montana: The Movie and the total box office ticket sales for the three-

day weekend.

8.3 Determining the Sample Size

In providing practical advice in the two preceding sections, we commented on the role of

the sample size in providing good approximate confidence intervals when the population is

not normally distributed. In this section, we focus on another aspect of the sample size issue.

We describe how to choose a sample size large enough to provide a desired margin of error.

To understand how this process works, we return to the σ known case presented in Section

8.1. Using expression (8.1), the interval estimate is

x¯

⫾

z

α/2

σ

兹

n

If a desired margin of error

is selected prior to

sampling, the procedures in

this section can be used to

determine the sample size

necessary to satisfy the

margin of error

requirement.

file

WEB

Program

file

WEB

Alcohol

file

WEB

TicketSales

CH008.qxd 8/16/10 6:38 PM Page 321

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).

Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

The quantity z

α/2

( ) is the margin of error. Thus, we see that z

α/2

, the population stan-

dard deviation σ, and the sample size n combine to determine the margin of error. Once we

select a confidence coefficient, 1 ⫺ α, z

α/2

can be determined. Then, if we have a value for

σ, we can determine the sample size n needed to provide any desired margin of error.

Development of the formula used to compute the required sample size n follows.

Let E ⫽ the desired margin of error:

Solving for , we have

Squaring both sides ofthis equation,we obtainthe following expression for thesample size.

兹

n ⫽

z

α/2

σ

E

兹

n

E ⫽ z

α/2

σ

兹

n

σ兾

兹

n

322 Chapter 8 Interval Estimation

This sample size provides the desired margin of error at the chosen confidence level.

In equation (8.3), E is the margin of error that the user is willing to accept, and the value

of z

α/2

follows directly from the confidence level to be used in developing the interval esti-

mate. Although user preference must be considered, 95% confidence is the most frequently

chosen value (z

.025

⫽ 1.96).

Finally, use of equation (8.3) requires a value for the population standard deviation σ.

However, even if σ is unknown, we can use equation (8.3) provided we have a preliminary

or planning value for σ. In practice, one of the following procedures can be chosen.

1. Use the estimate of the population standard deviation computed from data of previ-

ous studies as the planning value for σ.

2. Use a pilot study to select a preliminary sample. The sample standard deviation from

the preliminary sample can be used as the planning value for σ.

3. Use judgment or a “best guess” for the value of σ. For example, we might begin by

estimating the largest and smallest data values in the population. The difference be-

tween the largest and smallest values provides an estimate of the range for the data.

Finally, the range divided by 4 is often suggested as a rough approximation of the

standard deviation and thus an acceptable planning value for σ.

Let us demonstrate the use of equation (8.3) to determine the sample size by consider-

ing the following example. A previous study that investigated the cost of renting automo-

biles in the United States found a mean cost of approximately $55 per day for renting a

midsize automobile. Suppose that the organization that conducted this study would like to

conduct a new study in order to estimate the population mean daily rental cost for a midsize

automobile in the United States. In designing the new study, the project director specifies

that the population mean daily rental cost be estimated with a margin of error of $2 and a

95% level of confidence.

The project director specified a desired margin of error of E ⫽ 2, and the 95% level of

confidence indicates z

.025

⫽ 1.96. Thus, we need only a planning value for the population

standard deviation σ in order to compute the required sample size.At this point, an analyst

reviewed thesample data fromthe previous studyand found that the sample standard devia-

tion for the daily rental cost was $9.65. Using 9.65 as the planning value for σ, we obtain

SAMPLE SIZE FOR AN INTERVAL ESTIMATE OF A POPULATION MEAN

(8.3)

n ⫽

(z

α/2

)

2

σ

2

E

2

Equation (8.3) can be used

to provide a good sample

size recommendation.

However, judgment on the

part of the analyst should

be used to determine

whether the final sample

size should be adjusted

upward.

A planning value for the

population standard

deviation σ must be

specified before the sample

size can be determined.

Three methods of obtaining

a planning value for σ are

discussed here.

CH008.qxd 8/16/10 6:38 PM Page 322

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).

Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

8.3 Determining the Sample Size 323

Thus, the sample size for the new study needs to be at least 89.43 midsize automobile rentals

in order to satisfy the project director’s $2 margin-of-error requirement. In cases where the

computed n is not an integer, we round up to the next integer value; hence, the recom-

mended sample size is 90 midsize automobile rentals.

Exercises

Methods

23. How large a sample should be selected to provide a 95% confidence interval with a mar-

gin of error of 10? Assume that the population standard deviation is 40.

24. The range for a set of data is estimated to be 36.

a. What is the planning value for the population standard deviation?

b. At 95% confidence, how large a sample would provide a margin of error of 3?

c. At 95% confidence, how large a sample would provide a margin of error of 2?

Applications

25. Refer to the Scheer Industries example in Section 8.2. Use 6.84 days as a planning value

for the population standard deviation.

a. Assuming 95% confidence, what sample size would be required to obtain a margin of

error of 1.5 days?

b. If the precision statement was made with 90% confidence, what sample size would be

required to obtain a margin of error of 2 days?

26. The average cost of a gallon of unleaded gasoline in Greater Cincinnati was reported to be

$2.41 (The Cincinnati Enquirer, February 3, 2006). During periods of rapidly changing

prices, the newspaper samples service stations and prepares reports on gasoline prices fre-

quently. Assume the standard deviation is $.15 for the price of a gallon of unleaded regu-

lar gasoline, and recommend the appropriate sample size for the newspaper to use if it

wishes to report a margin of error at 95% confidence.

a. Suppose the desired margin of error is $.07.

b. Suppose the desired margin of error is $.05.

c. Suppose the desired margin of error is $.03.

27. Annual starting salaries for college graduates with degrees in business administration are

generally expected to be between $30,000 and $45,000. Assume that a 95% confidence in-

terval estimate of the population mean annual starting salary is desired. What is the plan-

ning value for the population standard deviation? How large a sample should be taken if

the desired margin of error is

a. $500?

b. $200?

c. $100?

d. Would you recommend trying to obtain the $100 margin of error? Explain.

28. An online survey by ShareBuilder, a retirement plan provider, and Harris Interactive re-

ported that 60% of female business owners are not confident they are saving enough for

retirement (SmallBiz, Winter 2006). Suppose we would like to do a follow-up study to de-

termine how much female business owners are saving each year toward retirement and

want to use $100 as the desired margin of error for an interval estimate of the population

mean. Use $1100 as a planning value for the standard deviation and recommend a sample

size for each of the following situations.

a. A 90% confidence interval is desired for the mean amount saved.

b. A 95% confidence interval is desired for the mean amount saved.

n ⫽

(z

α/2

)

2

σ

2

E

2

⫽

(1.96)

2

(9.65)

2

⫽ 89.43

Equation (8.3) provides the

minimum sample size

needed to satisfy the

desired margin of error

requirement. If the

computed sample size is not

an integer, rounding up to

the next integer value will

provide a margin of error

slightly smaller than

required.

test

SELF

test

SELF

CH008.qxd 8/16/10 6:38 PM Page 323

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).

Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

324 Chapter 8 Interval Estimation

c. A 99% confidence interval is desired for the mean amount saved.

d. When the desired margin of error is set, what happens to the sample size as the confi-

dence level is increased? Would you recommend using a 99% confidence interval in

this case? Discuss.

29. The travel-to-work time for residents of the 15 largest cities in the United States is reported

in the 2003 Information Please Almanac. Suppose that a preliminary simple random

sample of residents of San Francisco is used to develop a planning value of 6.25 minutes

for the population standard deviation.

a. If we want to estimate the population mean travel-to-work time for San Francisco resi-

dents with a margin of error of 2 minutes, what sample size should be used? Assume

95% confidence.

b. If we want to estimate the population mean travel-to-work time for San Francisco resi-

dents with a margin of error of 1 minute, what sample size should be used? Assume

95% confidence.

30. During the first quarter of 2003, the price/earnings (

P/E) ratio for stocks listed on the New

York Stock Exchange generally ranged from 5 to 60 (The Wall Street Journal, March 7,

2003). Assume that we want to estimate the population mean

P/E ratio for all stocks listed

on the exchange. How many stocks should be included in the sample if we want a margin

of error of 3? Use 95% confidence.

8.4 Population Proportion

In the introduction to this chapter we said that the general form of an interval estimate of a

population proportion p is

The sampling distribution of plays a key role in computing the margin of error for this in-

terval estimate.

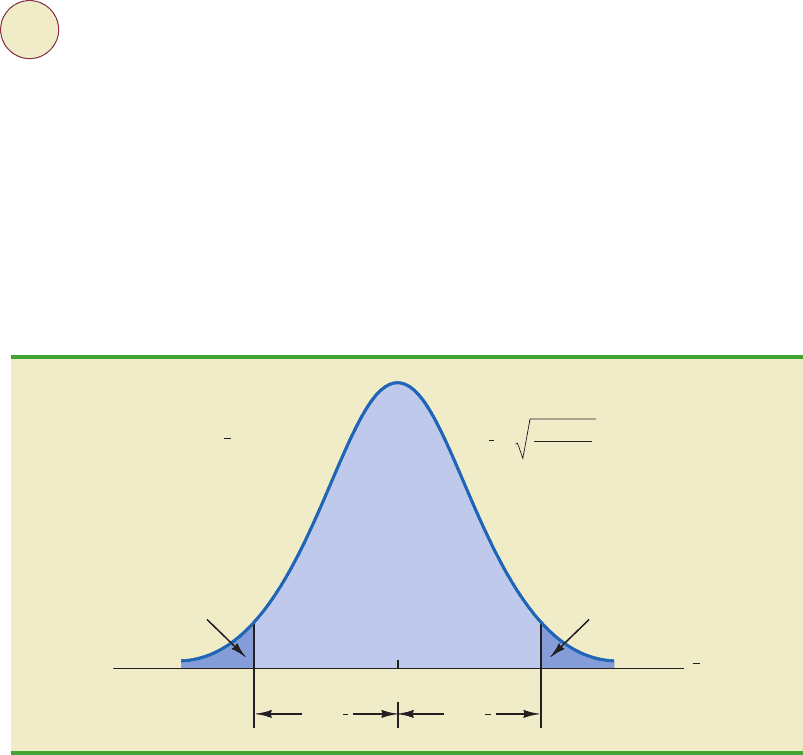
In Chapter 7 we said that the sampling distribution of can be approximated by a normal

distribution whenever np ⱖ 5 and n(1 ⫺ p) ⱖ 5. Figure 8.9 shows the normal approximation

p¯

⫾

Margin of error

p

Sampling distribution

of p

p

σ

p

=

p(1 – p)

n

α

/2

z

α

/2

α

/2

σ

p

z

α

/2

σ

p

FIGURE 8.9 NORMALAPPROXIMATION OF THE SAMPLING DISTRIBUTION OF p¯

CH008.qxd 8/16/10 6:38 PM Page 324

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).

Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

Anderson D.R., Sweeney D.J., Williams T.A. Essentials of Statistics for Business and Economics

Подождите немного. Документ загружается.