API RP 2A-WSD-2007 Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms-Working Stress Design

Подождите немного. Документ загружается.

RECOMMENDED PRACTICE FOR PLANNING, DESIGNING AND CONSTRUCTING FIXED OFFSHORE PLATFORMS—WORKING STRESS DESIGN 139

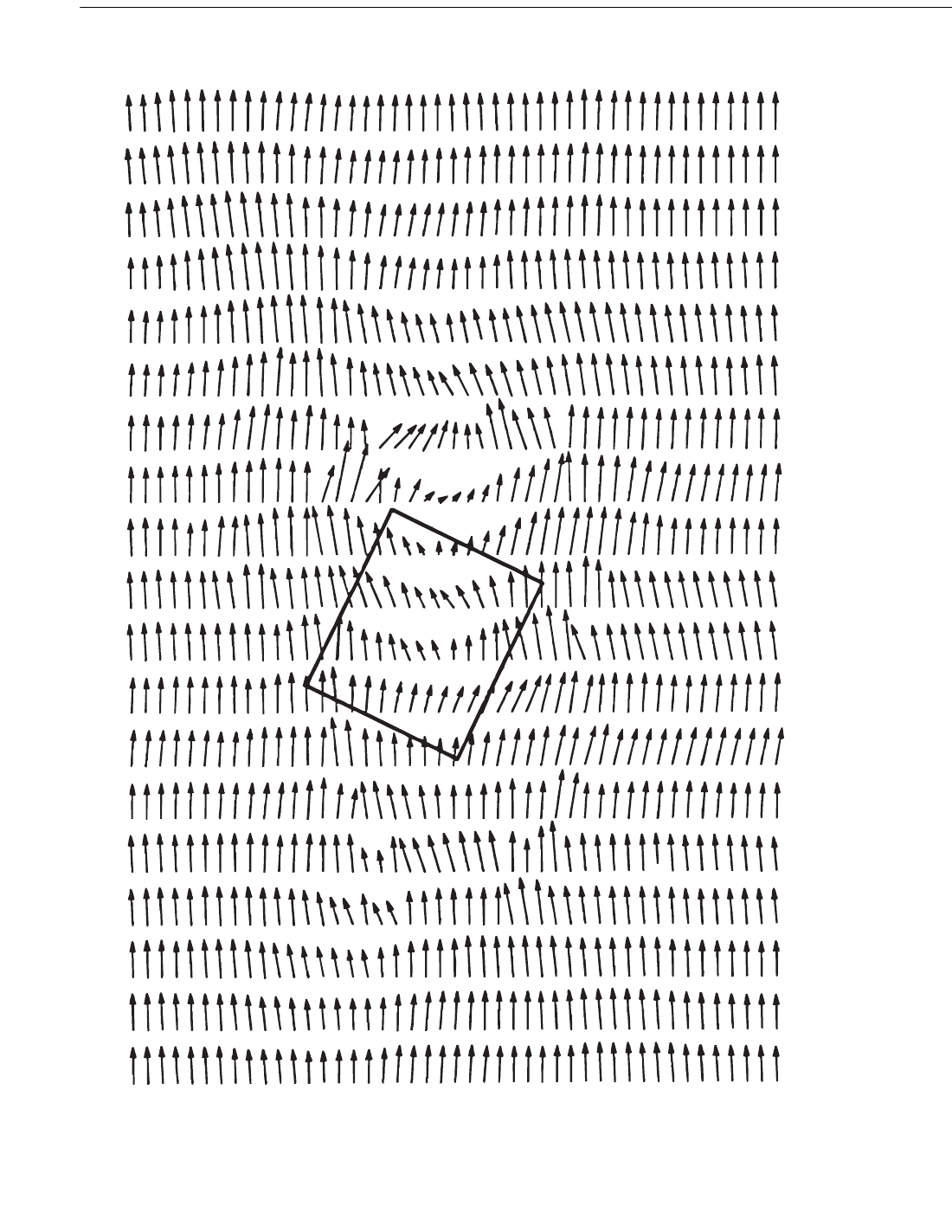
Figure C2.3.1-1—Current Vectors Computed from Doppler Measurements at 60 ft

on the Bullwinkle Platform (100 cm/s →)

Provided by IHS under license with API

Licensee=Indonesia location/5940240008

Not for Resale, 10/22/2008 00:07:12 MDT

--`,,```,,,`,,,,,,,,,,,,,,`,``,`-`-`,,`,,`,`,,`---

140 API RECOMMENDED PRACTICE 2A-WSD

are within +1 to –4 percent of those produced by the exact

solution on a typical drag-dominant structure subjected to

representative waves and current profiles.

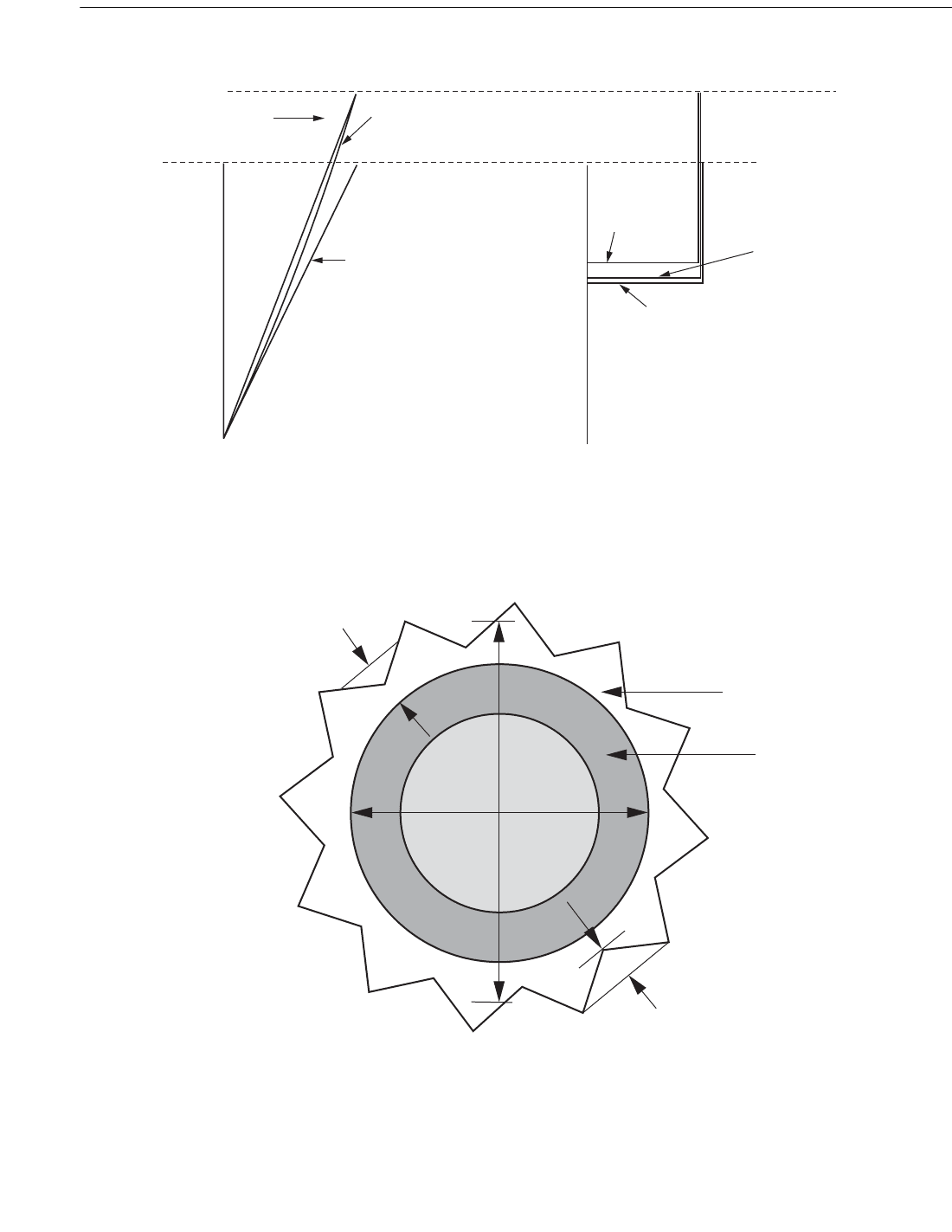
Another acceptable approximate model for many applica-

tions is one that uses a linearly stretched current profile, with

z + d = (z´ + d) (d + η)/d

The stretched current profiles from the two models are

compared qualitatively in Figure C2.3.1-2 for typical

sheared and slab current profiles under a wave crest. The

linearly stretched current produces global loads on a typical

drag-dominant platform that are nearly as accurate as those

produced by the nonlinearly stretched current, being within

0 to –6 percent of loads produced by the exact solution.

However, it does not simulate the combined wave/current

velocity profile from the exact solution as faithfully as non-

linear stretching.

Vertical extrapolation of the input current profile above

mean water level produces reasonably accurate estimates of

global loads on drag-dominant platforms in most cases. In

particular, for a slab profile thicker than about 50 m, like the

recommended profiles in Section 2.3.4, vertical extrapolation

produces nearly the same result as nonlinear stretching, as

illustrated in Figure C2.3.1-2. However, if the specified pro-

file U

(z) has a very high speed at mean water level, sheared

to much lower speeds just below mean water level, the global

force may be overestimated (by about 8 percent in a typical

application).

Another approximate model is the linearly stretched model

described above, adjusted so that the total momentum in the

stretched profile from the seafloor to the wave surface equals

that in the specified profile from the seafloor to mean water

level. This procedure is not supported by the theoretical anal-

yses of Dalrymple and Heideman (1989) or Eastwood and

Watson (1989).

If the current is not in the same direction as the wave, the

methods discussed above may still be used, with one modifi-

cation. Both the in-line and normal components of current

would be stretched, but only the in-line component would be

used to estimate T

app

for the Doppler-shifted wave.

While no exact solution has been developed for irregular

waves, the wave/current solution for regular waves can be

logically extended. In the first two approximations described

above for regular waves, the period and length of the regular

wave should be replaced with the period and length corre-

sponding to the spectral peak frequency.

C2.3.1b6 Marine Growth

All elements of the structure (members, conductors, risers,

appurtenances, etc.) are increased in cross-sectional area by

marine growth. The effective element diameter (cross-sec-

tional width for non-circular cylinders, or prisms) is D = D

2t, where D

is the “clean” outer diameter and t is the average

growth thickness that would be obtained by circumferential

measurements with a 1 inch to 4 inch-wide tape. An addi-

tional parameter that affects the drag coefficient of elements

with circular cross-sections is the relative roughness, e = k/D,

where k is the average peak-to-valley height of “hard” growth

organisms. Marine growth thickness and roughness are illus-

trated in Figure C.2.3.1-3 for a circular cylinder. Marine

organisms generally colonize a structure soon after installa-

tion. They grow rapidly in the beginning, but growth tapers

off after a few years. Marine growth has been measured on

structures in many areas but must be estimated for other

areas.

C2.3.1b7 Drag and Inertia Coefficients

In the ocean environment, the forces predicted by Mori-

son’s equation are only an engineering approximation. Mori-

son’s equation can match measured drag and inertia forces

reasonably well in any particular half wave cycle with con-

stant C

and C

, but the best fit values of C

and C

vary

from one half wave cycle to another. Most of the variation in

and C

can be accounted for by expressing C

and C

functions of

Relative surface roughness e = k/D

Reynolds number R

= U

D/ν

Keulegan-Carpenter number K = 2U

Current/wave velocity ratio r = V

Member orientation

Here U

is the maximum velocity (including current) nor-

mal to the cylinder axis in a half wave cycle, T

is the dura-

tion of the half wave cycle, V

is the in-line (with waves)

current component, U

is the maximum wave-induced

orbital velocity, D is effective diameter (including marine

growth), ν is the kinematic viscosity of water, and k is the

absolute roughness height.

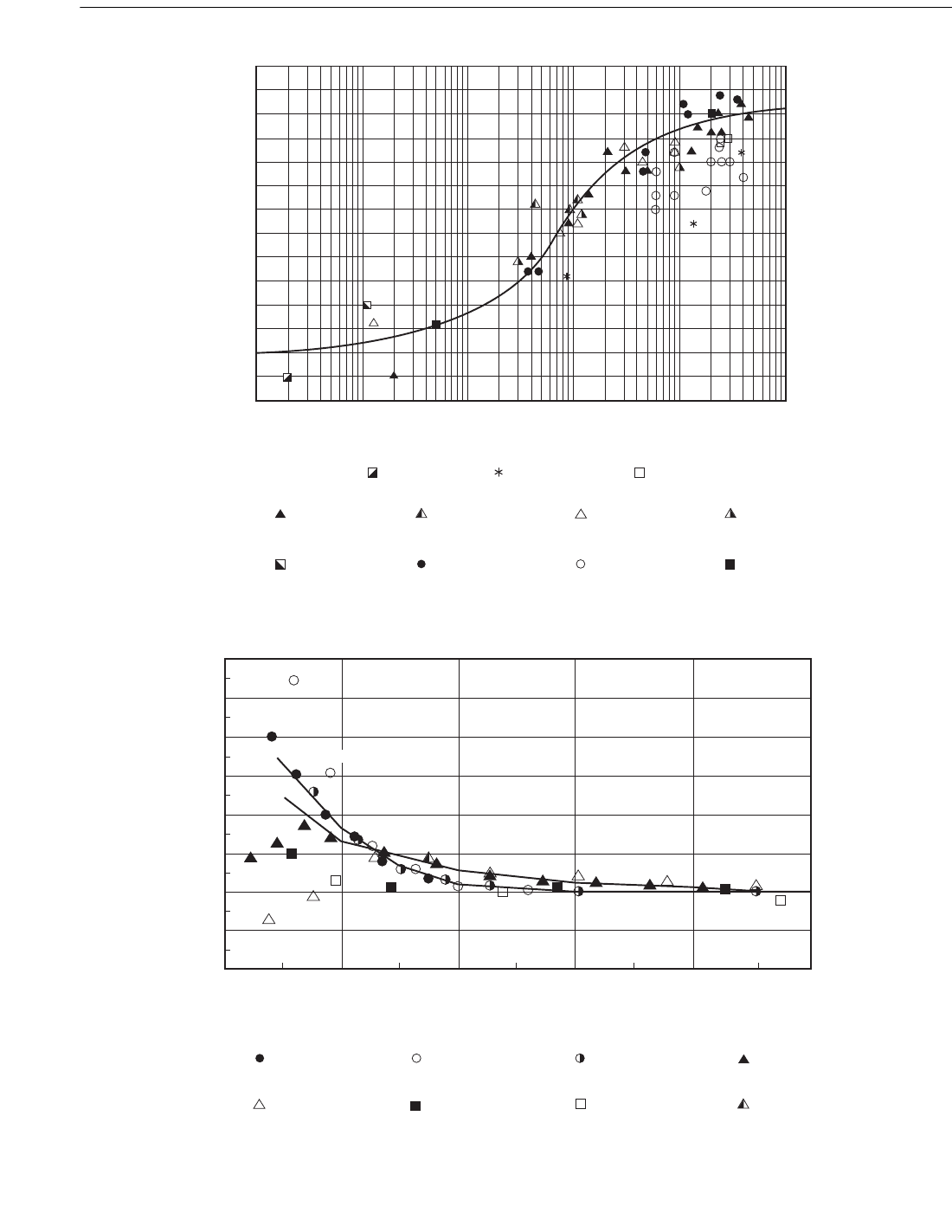
Surface Roughness. The dependence of C

, the steady-flow

drag coefficient at post-critical Reynolds numbers, on relative

surface roughness, is shown in Figure C2.3.1-4, for “hard”

roughness elements. All the data in this figure have been

adjusted, if necessary, to account for wind tunnel blockage

and to have a drag coefficient that is referenced to the effec-

tive diameter D, including the roughness elements.

Natural marine growth on platforms will generally have e

> 10

–3

. Thus, in the absence of better information on the

expected value of surface roughness and its variation with

depth for a particular site, it is reasonable to assume C

1.00 to 1.10 for all members below high tide level. One

would still need to estimate the thickness of marine growth

that will ultimately accumulate in order to estimate the

Provided by IHS under license with API

Licensee=Indonesia location/5940240008

Not for Resale, 10/22/2008 00:07:12 MDT

--`,,```,,,`,,,,,,,,,,,,,,`,``,`-`-`,,`,,`,`,,`---

RECOMMENDED PRACTICE FOR PLANNING, DESIGNING AND CONSTRUCTING FIXED OFFSHORE PLATFORMS—WORKING STRESS DESIGN 141

Figure C2.3.1-2—Comparison of Linear and Nonlinear Stretching of Current Profiles

Figure C2.3.1-3—Definition of Surface Roughness Height and Thickness

Shear profile

Linear

stretch

Nonlinear

stretch

Input

profile

Linear

stretch

Nonlinear

stretch

Input

profile

MWL

Crest

Slab profile

Hard growth

Pipe

e = k/D

D = D

+ 2t

Provided by IHS under license with API

Licensee=Indonesia location/5940240008

Not for Resale, 10/22/2008 00:07:12 MDT

--`,,```,,,`,,,,,,,,,,,,,,`,``,`-`-`,,`,,`,`,,`---

142 API RECOMMENDED PRACTICE 2A-WSD

effective diameter D. For members above high tide level, a

reasonable estimate of surface roughness is k = 0.002 inches

(0.05 mm), which will give C

in the range 0.6 to 0.7 for

typical diameters.

All the data in Figure C2.3.1-4 are for cylinders that are

densely covered with surface roughness elements. Force mea-

surements (Kasahara and Shimazaki, 1987; Schlichting,

1979) show that there is little degradation in the effectiveness

of surface roughness for surface coverage as sparse as 10%,

but that roughness effects are negligible for surface coverage

less than 3%.

The effect of soft, flexible growth on C

is poorly under-

stood. Tests run by Nath (1987) indicate that (a) soft, fuzzy

growth has little effect, C

being determined predominantly

by the underlying hard growth; and (b) anemones and kelp

produce drag coefficients similar to those for hard growth.

For cylindrical members whose cross section is not circu-

lar, C

may be assumed to be independent of surface rough-

ness. Suitable values are provided by DnV (1977).

Surface roughness also affects the inertia coefficient in

oscillatory flow. Generally, as C

increases with roughness,

decreases. More information is provided in subsequent

discussions.

Reynolds Number. The force coefficients for members

whose cross sections have sharp edges are practically inde-

pendent of Reynolds number. However, circular cylinders

have coefficients that depend on Reynolds number.

Fortunately, for most offshore structures in the extreme

design environment, Reynolds numbers are well into the

post-critical flow regime, where C

for circular cylinders is

independent of Reynolds number. However, in less severe

environments, such as considered in fatigue calculations,

some platform members could drop down into the critical

flow regime. Use of the post critical C

in these cases would

be conservative for static wave force calculations but noncon-

servative for calculating damping of dynamically excited

structures.

In laboratory tests of scale models of platforms with circu-

lar cylindrical members, one must be fully aware of the

dependence of C

on Reynolds number. In particular, the

scale of the model and the surface roughness should be cho-

sen to eliminate or minimize Reynolds number dependence,

and the difference between model-scale and full-scale C

should be considered in the application of model test results

to full-scale structures. Further guidance on the dependence

of circular cylinder C

on Reynolds number can be found in

Achenbach (1971), Hoerner (1965), and Sarpkaya and Isaac-

son (1981).

Keulegan-Carpenter Number. This parameter is a measure

of the unsteadiness of the flow; it is proportional to the dis-

tance normal to the member axis traveled by an undisturbed

fluid particle in a half wave cycle, normalized by the member

diameter. For a typical full-scale jacket structure in design

storm conditions, K is generally greater than 40 for members

in the ‘wave zone’, and drag force is predominant over inertia

force. On the other hand, for the large-diameter columns of a

typical gravity structure, K may be less than 10 and inertia

force is predominant over drag force.

The parameter K is also a measure of the importance of

“wake encounter” for nearly vertical (within 15° of vertical)

members in waves. As the fluid moves across a member, a

wake is created. When oscillatory flow reverses, fluid parti-

cles in the wake return sooner and impact the member with

greater velocity than undisturbed fluid particles. For larger K,

the wake travels farther and decays more before returning to

the cylinder and, furthermore, is less likely to strike the cylin-

der at all if the waves are multidirectional or there is a compo-

nent of current normal to the principal wave direction. For

very large K, wake encounter can be neglected. For smaller

K, wake encounter amplifies the drag force for nearly vertical

members above its quasi-steady value estimated from undis-

turbed fluid velocities.

Figure C2.3.1-5 shows data for the drag coefficient C

that

are most appropriate for calculating loads on nearly vertical

members in extreme storm environments. All these data were

obtained in the post-critical flow regime, in which C

practically independent of Reynolds number. All account for

wave spreading, that is, all have two components of motion

normal to the member axis. All except the ‘figure 8’ data

implicitly account for random wave motion. The field data

also naturally include an axial component of motion and, to

some extent, a steady current. The data for smooth and rough

cylinders are reasonably well represented by a single curve in

Figure C2.3.1-5, for K > 12, with K normalized by C

, as

suggested by the far-field, quasi-steady wake model of Beck-

mann and McBride (1968).

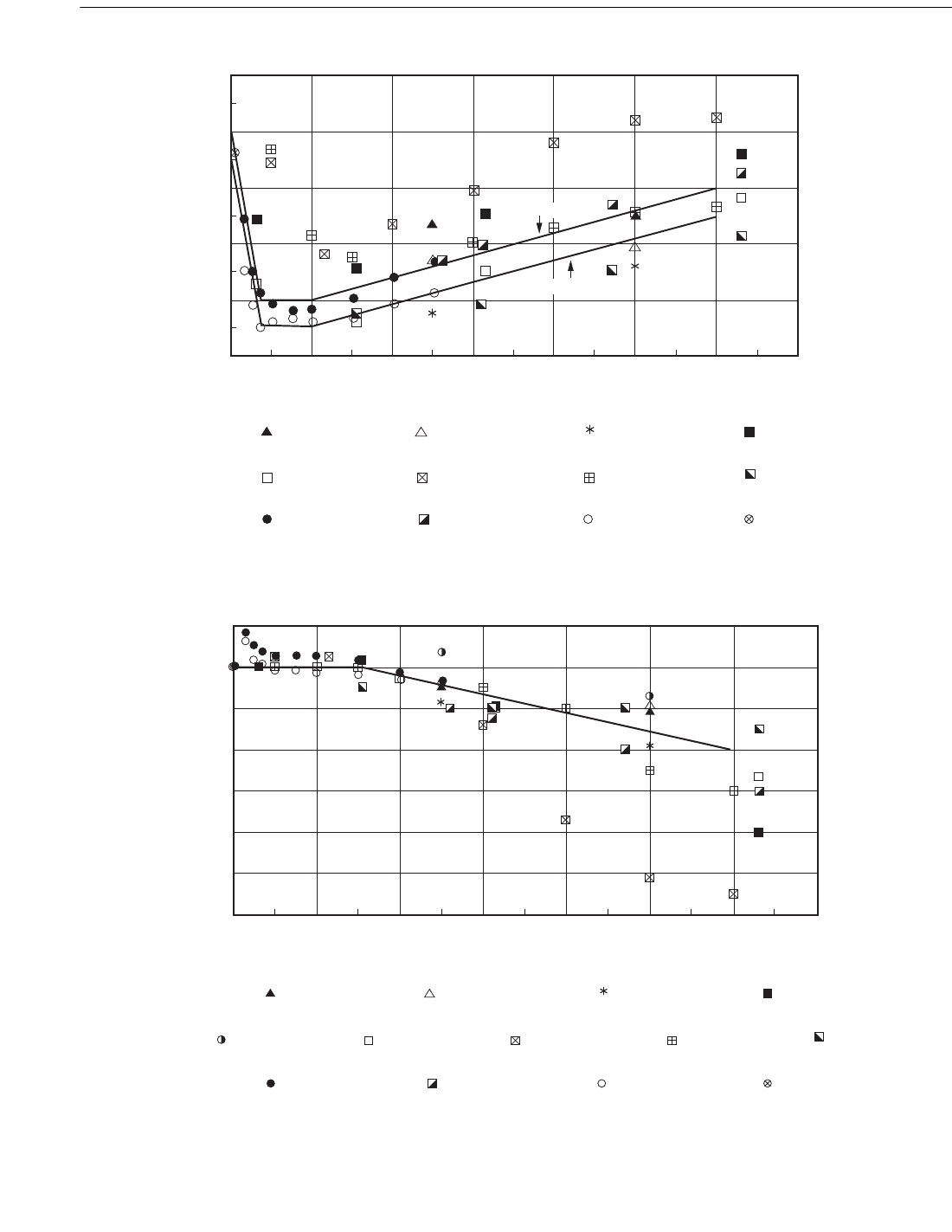
Figure C2.3.1-6 shows drag coefficient data for K < 12,

which are more appropriate for calculating loads on nearly

vertical members in less extreme sea states and drag damping

in earthquake-excited motion, for example. For K < 12, the

smooth and rough cylinder data are similar if K is not normal-

ized by C

. The data of Sarpkaya (1986) do not agree well

with the curves in Figure C2.3.1-6, presumably because of

the relatively low Reynolds number in his tests for the lowest

values of K and because of the lack of wave spreading in his

tests for the higher values of K.

It should be noted that the symbols shown in Figure

C2.3.1-5 do not represent individual data points. Rather, they

represent values from a curve fitted through a scatter of data

points. In designing a structure consisting of a single isolated

column, one should perhaps account for the scatter in the C

data. In this regard, the data of Sarpkaya (1986) for one-

dimensional, sinusoidally oscillating motion, which are nota-

bly omitted from Figure C2.3.1-5, represent a reasonable

upper bound. However, for a structure consisting of many

members, the scatter in C

can probably be neglected, as the

Provided by IHS under license with API

Licensee=Indonesia location/5940240008

Not for Resale, 10/22/2008 00:07:12 MDT

No reproduction or networking permitted without license from IHS

RECOMMENDED PRACTICE FOR PLANNING, DESIGNING AND CONSTRUCTING FIXED OFFSHORE PLATFORMS—WORKING STRESS DESIGN 143

Figure C2.3.1-4—Dependence of Steady Flow Drag Coefficient on Relative Surface Roughness

Figure C2.3.1-5—Wake Amplification Factor for Drag Coefficient as a Function of K/C

1.2

1.1

0.9

0.8

0.7

0.6

0.5

CDS

1E-06 1E-05 0.0001 0.001 0.01 0.1

Jones (1989) Blumberg (1961) Wolfram (1985)

Miller (1976) Szechenyl (1975) Achenbach (1971, 1981) Want (1986)

Roshko (1961) Norton (1983) Nath (1987) Rodenbusch (1983)

Rodenbusch (1983), CDS = 0.66

random directional

Rodenbusch (1983), CDS = 1.10

Figure 8

Rodenbusch (1983), CDS = 0.66

Figure 8

Heldeman (1979), CDS = 1.00 Heldeman (1979), CDS = 0.68 Bishop (1985), CDS = 0.66

Rodenbusch (1983), CDS = 1.10

random directional

Ohmart & Gratz (1979), CDS = 0.60

2.2

1.8

1.6

1.4

1.2

0.8

0.6

0 20 40 60 80 100

K/CDS

Lab data

Field data

Provided by IHS under license with API

Licensee=Indonesia location/5940240008

Not for Resale, 10/22/2008 00:07:12 MDT

--`,,```,,,`,,,,,,,,,,,,,,`,``,`-`-`,,`,,`,`,,`---

144 API RECOMMENDED PRACTICE 2A-WSD

deviations from the mean curve are uncorrelated from mem-

ber to member (see Heideman et al., 1979).

Figures C2.3.1-7 and C2.3.1-8 show data for the inertia

coefficient C

for a nearly vertical circular cylinder. Figure

C2.3.1-7 shows that C

for both smooth and rough cylin-

ders approaches the theoretical value of 2.0 for K ≤ 3. For K

> 3, with the onset of flow separation, C

begins to

decrease. With the exception of Sarpkaya’s rough cylinder

data, which exhibit a pronounced drop (‘inertia crisis’) in

at K ≈ 12, it appears that a single sloping line is adequate

for both smooth and rough cylinders, up to K ≈ 12, beyond

which smooth and rough cylinder data begin to diverge. In

Figure C2.3.1-8, the single line from Figure C2.3.1-7 is seen

to split into two lines because K is divided by C

= 0.66 for

smooth cylinders and C

= 1.1 for rough cylinders. The

vale of C

is taken as 1.6 for smooth cylinders and 1.2 for

rough cylinders for K/C

≥ 17.

Although Figures C2.3.1-5 through C2.3.1-8 are based on

circular cylinder data, they are also applicable to non-circular

cylinders, provided the appropriate value of C

is used, and

provided C

is multiplied by C

/2, where C

is the theoret-

ical value of C

for the non-circular cylinder as K → 0.

Furthermore, while Figs. C2.3.1-5 through C2.3.1-8 were

developed for use with individual, deterministic waves, they

can also be used for random wave analysis (either time or fre-

quency domain) of fixed platforms by using significant wave

height and spectral peak period to calculate K.

Current/Wave Velocity Ratio. The effect of a steady in-line

current added to oscillatory motion is to push C

toward C

its steady flow value. Data show that, for practical purposes,

= C

when the current/wave velocity ratio r is greater than

0.4. For r < 0.4, the effect of a steady in-line current can be

accommodated by modifying the Keulegan-Carpenter num-

ber. A first-order correction would be to multiply K due to

wave alone by (1 + r)2θ

/π, where θ

= arctan [ , –r].

A current component normal to the wave direction also

drives C

toward C

, since it reduces the impact of wake

encounter. Data show that, for practical purposes, C

= C

for V

D > 4. On the other hand, wake encounter has

nearly its full impact for V

D < 0.5.

Member Orientation: For members that are not nearly verti-

cal, the effect of wake encounter, as characterized by the K

dependence in Figs. C2.3.1-5 through C2.3.1-8, is small. For

horizontal and diagonal members, it is sufficient for engineer-

ing purposes to use the theoretical value of C

at K → 0 and

the steady-flow value of C

= C

at K → ∞.

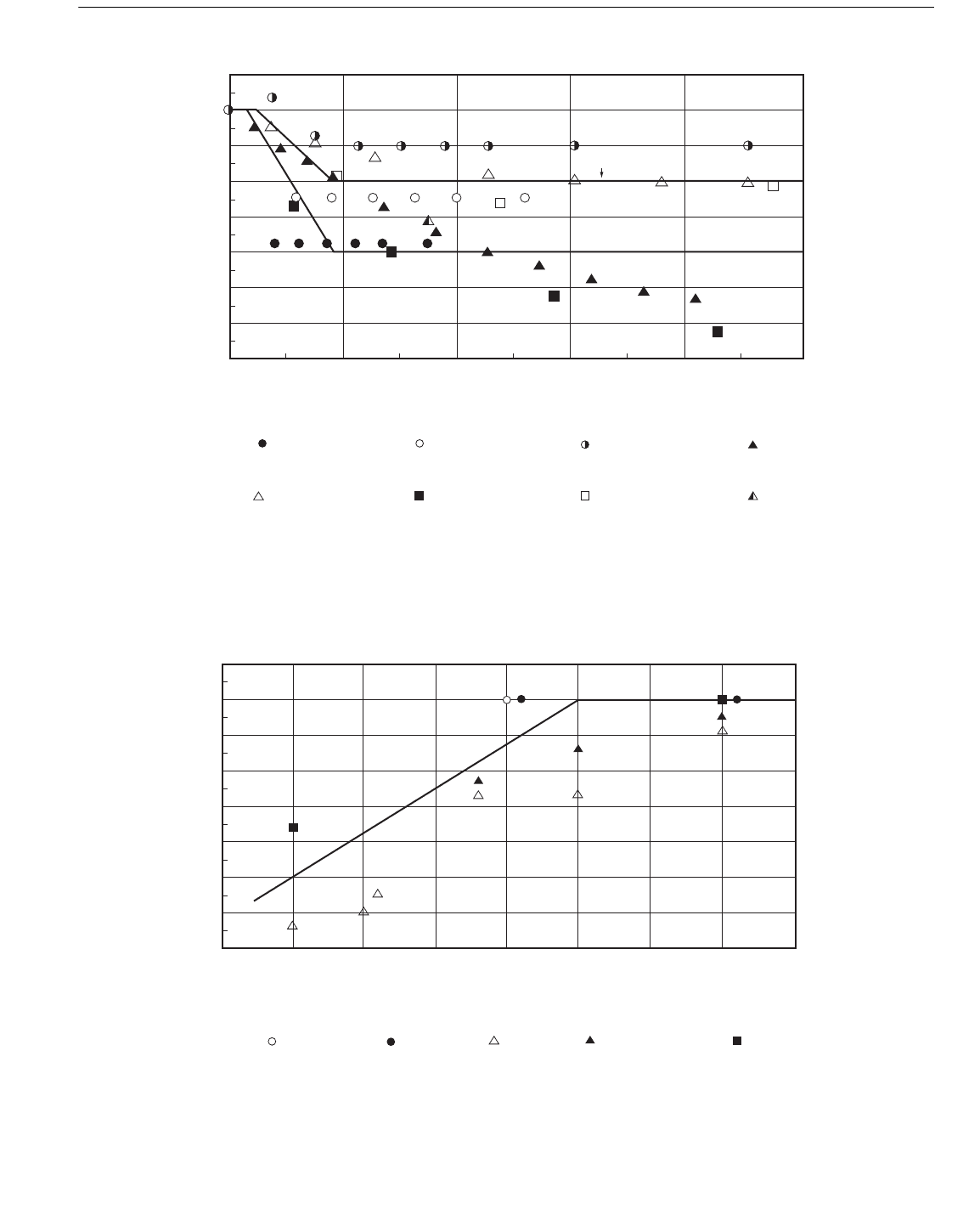
C2.3.1b8 Conductor Shielding Factor

The empirical basis for the shielding wave force reduction

factor for conductor arrays is shown in Figure C2.3.1-9. Data

from flow directions perfectly aligned with a row or column

of the array are excluded, for conservatism.

The data in Figure C2.3.1-9 are from steady flow tests and

oscillatory flow tests at very high amplitudes of oscillation.

Thus the factor is strictly applicable only in a steady current

with negligible waves or near the mean water level in very

large waves. The data of Heideman and Sarpkaya (1985)

indicate that the factor is applicable if A/S > 6, where A is the

amplitude of oscillation and S is the center-to-center spacing

of the conductors in the wave direction. The data of Reed et

al. (1990) indicate that range of applicability can be expanded

to A/S > 2.5. For lower values of A/S, there is still some

shielding, until A/S < 0.5 (Heideman and Sarpkaya, 1985).

With A ≈ U

app

/2π, where U

and T

app

are defined in

C2.3.1b7 and C2.3.1b1, respectively, the approximate shield-

ing regimes are:

• A/S > 2.5, asymptotic shielding, factor from Figure

C2.3.1-9.

• A/S < 0.5, no shielding factor = 1.0.

• 0.5 < A/S < 2.5, partial shielding.

In the absence of better information, the shielding factor in

the partial shielding regime can be linearly interpolated as a

function of A/S. Waves considered in fatigue analyses may

lie in the partial shielding regime.

C2.3.1b9 Hydrodynamic Models for

Appurtenances

The hydrodynamic model of a structure is used for the cal-

culation of wave forces which represent the forces on the

actual structure. The model need not explicitly include every

element of the structure provided the dimensions and/or force

coefficients for the included elements account for the contri-

bution of the forces on the omitted elements. The hydrody-

namic model should account for the effects of marine growth

and for flow interference effects (blockage and shielding)

where appropriate.

Appurtenances include sub-structures and elements such as

boat landings, fenders or bumpers, walkways, stairways,

grout lines, and anodes. Though it is beyond the scope of this

commentary to provide modeling guidance for every con-

ceivable appurtenance, some general guidance is provided.

Boat landings are sub-structures generally consisting of a

large number of closely spaced tubular members, particularly

on some of the older designs. If the members are modeled

individually, shielding effects, depending upon the wave

direction, can be accounted for in a manner similar to that for

conductor arrays. Another option is to model a boat landing

as either a rectangular solid or as one or more plates, with

directionally dependent forces. Some guidance for coeffi-

cients for solid shapes and plates can be found in Det norske

Veritas (1977).

Conductor guide frames may also be modeled as rectangu-

lar solids and sometimes as plates. In either case, different

coefficients are appropriate for vertical and horizontal forces.

1 r

–

Provided by IHS under license with API

Licensee=Indonesia location/5940240008

Not for Resale, 10/22/2008 00:07:12 MDT

--`,,```,,,`,,,,,,,,,,,,,,`,``,`-`-`,,`,,`,`,,`---

RECOMMENDED PRACTICE FOR PLANNING, DESIGNING AND CONSTRUCTING FIXED OFFSHORE PLATFORMS—WORKING STRESS DESIGN 145

Figure C2.3.1-6—Wake Amplification Factor for Drag Coefficient as a Function of K

Figure C2.3.1-7—Inertia Coefficient as a Function of K

Rodenbusch (1983), CDS = 0.66

sinusoidal

Sarpkaya (1986), CDS = 1.10 Sarpkaya (1986), CDS = 0.65

Rodenbusch (1983), CDS = 1.10

random directional

Rodenbusch (1983), CDS = 0.66

random directional

Bearman (1985), CDS = 0.60

Rodenbusch (1983), CDS = 1.10

sinusoidal

Garrison (1990), CDS = 0.65

Marin (1987), CDS = 1.10 Garrison (1990), CDS = 1.10 Marin (1987), CDS = 0.60

Iwaki (1991), CDS = 1.10

2.5

1.5

0.5

0246810

12 14

CD/CDS

Rough (C

= 1.2)

Smooth (C

= 0.6)

Rodenbusch (1983), CDS = 0.66

sinusoidal

Bishop (1985), CDS = 0.66

Sarpkaya (1986), CDS = 1.10 Sarpkaya (1986), CDS = 0.65

Rodenbusch (1983), CDS = 1.10

random directional

Rodenbusch (1983), CDS = 0.66

random directional

Bearman (1985), CDS = 0.60

Rodenbusch (1983), CDS = 1.10

sinusoidal

Garrison (1990), CDS = 0.65

Marin (1987), CDS = 1.10 Garrison (1990), CDS = 1.10 Marin (1987), CDS = 0.60

Iwaki (1991), CDS = 1.10

2.2

1.8

1.4

1.2

0.8

0246810

12 14

Provided by IHS under license with API

Licensee=Indonesia location/5940240008

Not for Resale, 10/22/2008 00:07:12 MDT

--`,,```,,,`,,,,,,,,,,,,,,`,``,`-`-`,,`,,`,`,,`---

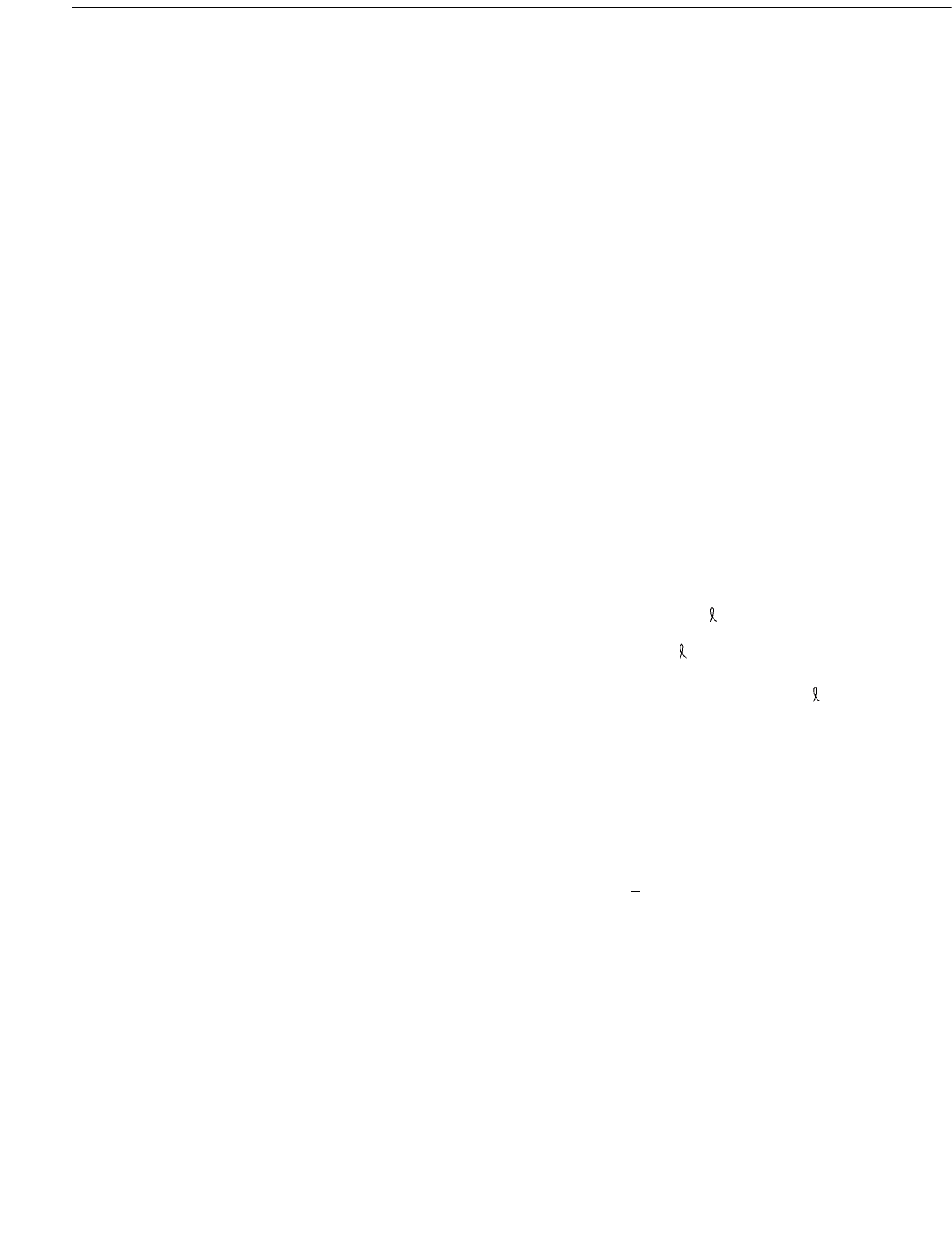
146 API RECOMMENDED PRACTICE 2A-WSD

Large fenders or boat bumpers and their supporting mem-

bers are usually modeled as individual members. They may

be treated as non-structural members provided that experi-

ence has shown their design to be adequate for their intended

purpose. Walkways, stairways, and grout lines may be mod-

eled as equivalent circular members though they are some-

times ignored where experience has proven the acceptability

of such action.

The treatment of anodes depends somewhat upon the num-

ber and size of the anodes on the structure. Anodes are often

ignored in the hydrodynamic model where experience has

shown that their wave force contribution is negligible. If they

are included, they can be modeled as equivalent circular cyl-

inders. Alternatively, anode wave forces may be approxi-

mated by increasing the diameters and/or force coefficients of

the member to which they are attached.

C2.3.1b10 Morison Equation

The use of the local acceleration rather than the total (local

plus convective) acceleration in the inertia term of Morison’s

equation is the subject of ongoing debate. There have been

several publications on this topic in recent years (Manners

and Rainey, 1992; Madsen, 1986; Sarpkaya and Isaacson,

Section 5.3.1, 1981; Newman, 1977). These publications all

conclude that the total acceleration should be used. However,

it must be noted that these publications all assume unrealisti-

cally that the flow does not separate from the cylinder. Realis-

tically, except for very small amplitudes of oscillation (K <

3), the flow separates on the downstream side of the cylinder,

creating a wake of reduced velocity. The local change in

velocity across the cylinder due to the convective acceleration

in the undisturbed far-field flow is generally much less than

the change in velocity due to local flow separation, as implied

in the paper by Keulegan and Carpenter (1958). The convec-

tive acceleration may also be nearly in phase with the locally

incident flow velocity, which leads the undisturbed far field

velocity in oscillatory flow because of “wake encounter”

(Lambrakos, et al., 1987). Therefore, it could be argued that

the convective acceleration should be neglected, either

because it is small relative to local velocity gradients due to

flow separation or because it is already implicitly included in

drag coefficients derived from measurements of local force in

separated flow. As a practical matter, the convective accelera-

tion exceeds 15% of the local acceleration only in steep

waves, for which inertia force is generally much smaller than

drag force (Sarpkaya and Isaacson, 1981).

Only the components of velocity and acceleration normal

to the member axis are used in computing drag and inertia

forces, based on the “flow independence,” or “cross-flow,”

principle. This principle has been verified in steady subcriti-

cal flow by Hoerner (1965) and in steady postcritical flow by

Norton, Heideman, and Mallard (1983). The data of Sarp-

kaya, et al. (1982), as reinterpreted by Garrison (1985), have

shown the flow independence principle to be also for inertia

forces in one-dimensional oscillatory flow. Therefore, it is

reasonable to assume that the flow independence principle is

valid in general for both steady and multidimensional oscilla-

tory flows, with the exception of flows near the unstable, crit-

ical Reynolds number regime.

C2.3.1b12 Local Member Design

The Morison equation accounts for local drag and inertia

forces but not for the “out of plane” (plane formed by the

velocity vector and member axis) local lift force due to peri-

odic, asymmetric vortex shedding from the downstream side

of a member. Lift forces can be neglected in the calculation of

global structure loads. Due to their high frequency, random

phasing, and oscillatory (with zero mean) nature, lift forces

are not correlated across the entire structure. However, lift

forces may need to be considered in local member design,

particularly for members high in the structure whose stresses

may be dominated by locally generated forces.

The oscillating lift force can be modeled as a modulated

sine function, whose frequency is generally several times the

frequency of the wave, and whose amplitude is modulated

with U

, where U is the time-varying component of fluid

velocity normal to the member axis. In the absence of

dynamic excitation, the maximum local lift force amplitude

max

per unit length of the member is related U

max

, the

maximum value of U during the wave cycle, by the equation

max

= C ,

max

(w/2g) DU

max

The coefficient C ,

max

has been found empirically by

Rodenbusch and Gutierrez (1988) to have considerable scat-

ter, with an approximate mean value C ,

max

≈ 0.7 C

, for

both smooth and rough circular cylinders, in both steady flow

and in waves with large Keulegan-Carpenter numbers. Sarp-

kaya (1986) focussed on the rms value of the oscillating lift

force and found that it was less than half F

L, max

The frequency of the oscillating lift force is St U

total

/D,

where St is the Strouhal number and U

total

is the total incident

velocity, including the axial component. Laboratory tests

(Norton et al., 1983; Rodenbusch and Gutierrez, 1983) have

shown that St ~

0.2 for circular cylinders over a broad range

of Reynolds numbers and flow inclination angles in steady

flow. If St remains constant in waves, than the frequency of

the oscillating lift force is also modulated as U varies with

time during a wave cycle.

In the event that any natural frequency of a member is near

the lift force frequency, a large amplitude dynamic response,

called vortex-induced-vibration (VIV), may occur. When

VIV occurs, the motion of the member and the magnitude of

the fluid-dynamic forces can increase to unacceptable levels.

VIV can occur on long spans due to wind forces in the con-

struction yard and on the tow barge as well as to waves and

currents on the in-place structure. A complete treatise on VIV

is beyond the scope of this commentary.

Provided by IHS under license with API

Licensee=Indonesia location/5940240008

Not for Resale, 10/22/2008 00:07:12 MDT

--`,,```,,,`,,,,,,,,,,,,,,`,``,`-`-`,,`,,`,`,,`---

RECOMMENDED PRACTICE FOR PLANNING, DESIGNING AND CONSTRUCTING FIXED OFFSHORE PLATFORMS—WORKING STRESS DESIGN 147

Figure C2.3.1-8—Inertia Coefficient as a Function of K/C

Figure C2.3.1-9—Shielding Factor for Wave Loads on Conductor Arrays as a Function of Conductor Spacing

2.2

1.8

1.4

1.2

0.8

0.6

0 20 40 60 80 100

K/CDS

Rodenbusch (1983), CDS = 0.66

Bishop (1985), CDS = 0.66

Rodenbusch (1983), CDS = 1.10

random directional

Rodenbusch (1983), CDS = 0.66

random directional

Rodenbusch (1983), CDS = 1.10

sinusoidal

Heldeman (1975), CDS = 1.00

Heldeman (1975), CDS = 1.68

Ohmart & Gratz (1979), CDS = 0.60

Rough (C

= 1.1)

Smooth (C

= 0.66)

1.1

0.9

0.8

0.7

0.6

0.5

0.4

0.3

1.5 2 2.5 3 3.5 5.5

4 4.5 5

S/D

Shielding Factor

Sterndorff (1990)

waves

Beckman (1979)

waves and current

Reed (1990)

current

Reed (1990)

waves (K = 126)

Heideman (1985)

waves (K = 250) and current

Provided by IHS under license with API

Licensee=Indonesia location/5940240008

Not for Resale, 10/22/2008 00:07:12 MDT

No reproduction or networking permitted without license from IHS

148 API RECOMMENDED PRACTICE 2A-WSD

Horizontal members in the wave splash zone of an in-place

structure may experience wave slam forces. These nearly ver-

tical forces are caused by the local water surface rising and

slapping against the underside of the member as a wave

passes. Since these forces are nearly vertical, they contribute

very little to the base shear and overturning moment of the

platform. However, slam forces may need to be considered in

local member design.

Slam forces can also occur on platform members over-

hanging the end of the barge while the platform is being

towed, or on members that strike the water first during side

launching of platforms.

In the theoretical case, slam force is impulsive. If the slam

force is truly impulsive, the member may be dynamically

excited. In the real world, the slam force may not be impul-

sive because of the three-dimensional shape of the sea sur-

face, the compressibility of air trapped between the member

and the sea surface, and the aerated nature of water near the

free surface.

Slam force F

per unit length can be calculated from the

equation

= C

(w/2g)DU

where U is the component of water particle velocity nor-

mal to the member axis at impact. Sarpkaya (1978) has

shown empirically that the coefficient C

may lie between 0.5

and 1.7 times its theoretical value of π, depending on the rise

time and natural frequency of the elastically mounted cylin-

der in his tests. Sarpkaya and Isaacson (1981) recommend

that if a dynamic response analysis is performed, the theoreti-

cal value of C

= π can be used; otherwise, a value of C

= 5.5

should be used.

Axial Froude-Krylov forces have the same form as the

inertia force in Morison’s equation, except that C

is set to

unity and the normal component of local acceleration is

replaced by the axial component. Axial Froude-Krylov forces

on members that are nearly vertical contribute negligibly to

platform base shear and overturning moment. Axial Froude-

Krylov forces on diagonal and horizontal braces are relatively

more important, contributing about 10% as much to base

shear and overturning moment as the inertia force included in

Morison’s equation, based on computations performed by

Atkins (1990). In view of approximations made elsewhere in

the computation of global wave force, axial Froude-Krylov

forces can generally be neglected.

References

(1) Achenbach, E., “Influence of Surface Roughness or the

Cross-Flow Around a Circular Cylinder,” Journal of Fluid

Mechanics, Vol., 46, pp. 321–335, 1971.

(2) Achenbach, E., and Heinecke, E., “On Vortex Shedding

from Smooth and Rough Cylinders in the Range of Reynolds

Numbers 6 × 10

to 5 × 10

,” Journal for Fluid Mechanics,

Vol. 109, pp. 239–251, 1981.

(3) Allender, J. H., and Petrauskas, C., “Measured and Pre-

dicted Wave Plus Current Loading on Laboratory-Scale

Space-Frame Structure,” Offshore Technology Conference,

OTC 5371, 1987.

(4) Atkins Engineering Services, “Fluid Loading on Fixed

Offshore Structures,” OTH 90 322, 1990.

(5) Bearman, P.W., Chaplin, J.R. Graham, J.M.R., Kostense,

J.R., Hall, P.F., and Klopman, G., “The Loading of a Cylinder

in Post-Critical Flow Beneath Periodic and Random Waves,”

Proceedings of Behavior of Offshore Structures Conference,

pp. 213–225, 1985.

(6) Beckmann, H., and McBride, C.M., “Inherent Scatter of

Wave Forces on Submerged Structures,” ASME Petroleum

Division Joint Conference with Pressure Vessels and Piping

Division, Dallas, September 22–25, 1968.

(7) Beckmann, H., and Merwin, J.E., “Wave Forces on Con-

ductor Pipe Group,” Proceedings of ASCE Civil Engineering

in the Oceans IV Conference, September 1979.

(8) Bishop, J.R., “Wave Force Data from the Second

Christchurch Bay Tower,” Offshore Technology Conference,

OTC 4953, 1985.

(9) Blumberg, R., and Rigg, A.M., “Hydrodynamic Drag at

Supercritical Reynolds Numbers,” ASME Conference, June

1961.

(10 )Chappelear, J.E., “Direct Numerical Calculation of

Wave Properties,” Journal of Geophysical Research, Vol., 66,

NO. 2, February 1961.

(11) Dalrymple, R.A., and Heideman, J.C., “Nonlinear Water

Waves on a Vertically-Sheared Current,” E&P Forum Work-

shop, “Wave and Current Kinematics and Loading,” Paris,

October 1989.

(12) Dean, R.G., and Perlin, M., “Intercomparison of Near-

Bottom Kinematics by Several Wave Theories and Field and

Laboratory Data,” Coastal Engineering, Elsevier Science

Publishers B. V., Amsterdam, The Netherlands, 1986.

(13) Det norske Veritas, “Rules for the Design, Construction,

and Inspection of Offshore Structures; Appendix B—Loads,”

1977.

(14) Eastwood, J.W., and Watson, C.J.H., “Implications of

Wave-Current Interactions for Offshore Design,” E & P

Forum Workshop, “Wave and Current Kinematics and Load-

ing,” Paris, October 1989.

(15) Forristall, G.Z., “Kinematics in the Crests of Storm

Waves,” 20th International Conference on Coastal Engineer-

ing, Taipei, 1986.

(16) Garrison, C.J., “Comments on Cross-Flow Principle and

Morison’s Equation,” ASCE Journal of Waterway, Port,

Provided by IHS under license with API

Licensee=Indonesia location/5940240008

Not for Resale, 10/22/2008 00:07:12 MDT

No reproduction or networking permitted without license from IHS