Аракелян А.К., Афанасьев А.А. Вентильные электрические машины и регулируемый электропривод. Книга 1
Подождите немного. Документ загружается.


31
A
5
. Для окрестности в плоскости
t
имеем:
t a R e R e
j l
5 5 5
, (
R
5
0 ) . (1.18)
После подставки (1.18) в (1.1) с учетом (1.16) будет иметь:
dz j C
a x x x
x x x x
d
1 3 4 7
1 2 5
6
. (1.19)
Интегрируя (1.19) по дуге с бесконечно малым радиусом
и учитывая величины изменения
z
и
(соответственно
j
и
( ) ), получим с учетом формулы (1.13) седьмое уравнение
для исходной системы:
a x x x x x x x
n
1 3 4 7 1 2 5
6
2
( ) . (1.20)
Регуляризация определенных интегралов (1.5) от функции
( )
t
с разрывами типа бесконечности в некоторых точках
t x
j
производится путем вычитания от нее и одновремен-
но сложения с ней другой функции (
1
( )
t
), совпадающей в
точке разрыва с исходной функцией [123, 258]
( ) ( ) ( ) ( )
t t t t
1 1
. (1.21)
Разность этих функций:
( ) ( ) ( )
t t t
1
уже не будет содержать особенности в данной точке
( ( )
x
j
0 ), и определенный интеграл от нее находится чис-
ленным методом, а интеграл от третьего слагаемого (1.21)
(функции
1
( )
t
) может быть найден аналитическим путем.

32
Причем:
1
1
( ) ( )
t D t x
j
j
,
где
D
t
t x
t x
j
j
j
lim
( )
( )
1
.
С учетом сказанного уравнения системы (1.6) для функ-
ции ( )
t
вида (1.17) примут форму
f t dt D x a
a
x
1 1 1 1 1
2
1
1
( ) , (1.22)
где
1
1
1
( )
t t
D
t x
n
( ) ;
D
x
x a x x x x x x
x x x x x x
n
1
1
1 1 1 3 1 4 1 7
1 2 1 5 1
6
( )( )( )( )
( )( )( )
;
1 1
0( )
x
.
f t dt D D x x
x
x
2 2 1 2 2 1
2
1
2
( ) ( ) , (1.23)
где
2
1
1
2
2
( )
t t
D
t x
D
t x
n
( ) ;
D
x
x a x x x x x x
x x x x x x
n
2
2
2 1 2 3 2 4 2 7
2 1 2 5 2
6
( )( )( )( )
( )( )( )
;

33
2 1
2
1 2
( )
x
D
x x
;
2 2
1
1 2
( )
x
D
x x
.
f t dt D x x
x
x
3 3 2 3 2
2
2
3
( ) , (1.24)
где
3
2
2
( )
t t
D
t x
n
( ) ;
3 2
0( )
x
.
f t dt D x x
x
x
4 4 5 5 4
2
4
5
( ) , (1.25)
где
4
5
5
( )
t t
D
t x
n
( ) ;
D
x
x a x x x x x x
x x x x x x
n
5
5
5 1 5 3 5 4 5 7
5 1 5 2 5
6
( )( )( )( )
( )( )( )
;
4 5
0( )
x
.
f t dt D D x x
x
x
5 5 5
6 6
5
2
5
6
( ) ( ) , (1.26)
где
5
5
5
6
6
( )
t t
D
t x
D
t x
n
( ) ;

34
D
x
x a x x x x x x
x x x x x x
n
6
6
6
1
6
3
6
4
6
7
6
1
6
2
6
5
( )( )( )( )
( )( )( )
;
5 5
6
5
6
( )
x
D
x x
;
5
6
5
5
6
( )
x
D
x x
.
f t dt t dt D
x
x
x
x
6 6
0
6
0
0
3
4
3
4
( ) ( ) ln , (1.27)
где
6
0
( )
t t
D
t
n
( ) ;
D
a x x x
x x x x
n
0
1 3 4 7
1 2 5
6
;
6
0 0( ) .
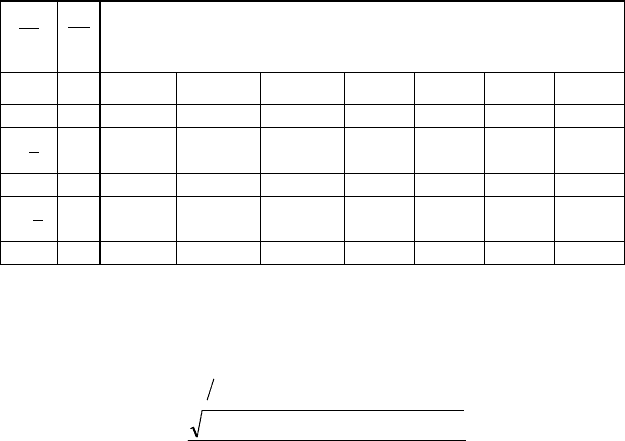
В табл.1.1 приведены результаты решения уравнения (1.6)
методом дифференциального продолжения решения по па-
раметру для различных значений глубин пазов
h
1
и
h
2
при
следующих исходных данных
3
:
b b b
n
1 2 3
2
5 3 2 0 255 10
; ; ; , м.
Для областей с бесконечно глубокими пазами, содержа-
щих, допустим,
Q
пазов, первые
Q
+1 уравнения исходной
системы (1.6) будут алгебраическими (безинтегральными).
Они получаются путем предельных преобразований диффе-
ренциального уравнения (1.1) в окрестностях точек, соответ-
ствующих открытым вершинам пазов и зазора. Это можно
проиллюстрировать на примере восьмиугольной области
рис. 1.2. Для нее имеем:
3
Òочность расчетов интегралов: относительная погрешность -10
-10
;
абсолютная погрешность -10
-15
; окончание итерационного процес-
са при максимальной невязке - 10
-7
. Для бесконечно глубоких па-
зов эти показатели имели соответственно значения: 10
-15
; 0; 10
-10
.
35
Òаблица1.1
h
1
h
2
Значения постоянных
a
2
a
3
a
4
a
6
a
7
a
8
a
9
5 3 -2.5360
-2.0292
-0.2876
2.4390
27.935
40.235
824.65
8
1
3
5 -2.3093
-2.2468
-0.2893
2.4510
32.735
34.238
819.93
12.5
7.5
-2.2802
-2.2757
-0.2894
2.4512
33.422
33.532
819.86
16
2
3
10
-2.2781
-2.2778
-0.2894
2.4512
33.473
33.481
819.85
-2.2781
-2.2781
-0.2894
2.4513
33.475
33.475
819.83
a
1
=
—10;
a
4 =
0;
a
8
=
;
x
T
x x x a a a a a
1 2 5 2 3 5
6
7
.
Поскольку
n
*
=
7 по формулам (1.2), (1.13), (1.4) найдем:
C
t
t a t x t x t x
t t x t x
n
;
( )
( )( )( )( )
( )( )
.
1 2 3 5
1 4
(1.28)
Первые три уравнения системы (1.6) получаются путем ин-
тегрирования уравнения (1.1) по дуге с бесконечно малым
радиусом в верхних полуокрестностях точек
a
2
; a
4
; a
6
.
Такому
движению изображающей точки в плоскости
t
соответствует
смещение ее образа в плоскости
z
соответственно на вели-
чины:
b j b
2 1
; ;( ) .
Например , для окрестности точки
a
2
имеем:
t a R e R dt jR e d
j j
2 2 2 2
, ( ) ; . (1.29)
После подстановки (1.29) в (1.28) получим:
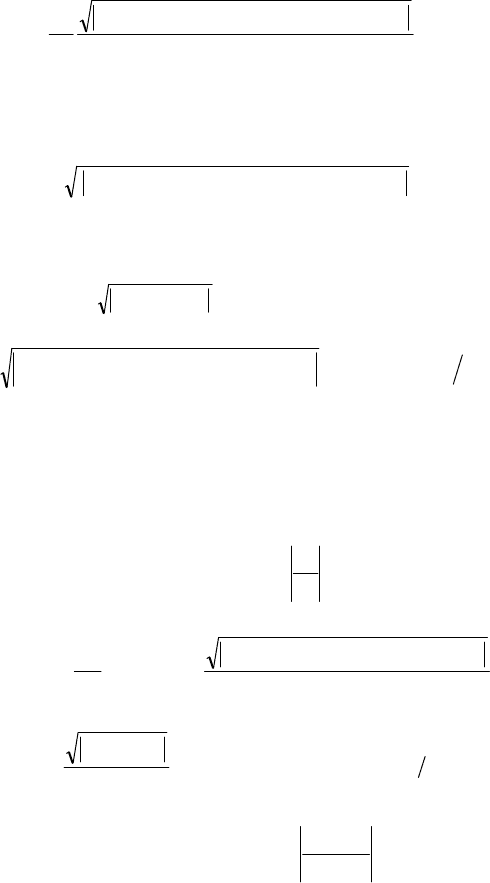
36
dz
x a x x x x x x
x x x
d
n
( )( )( )( )
( )
1 1 1 2 1 3 1 5
1 4
.
Интегрирование этого уравнения и двух аналогичных дает
выражения:
f x a x x x x x x
1 1 1 1 2 1 3 1 5
( )( )( )( )
b x x x l
n
2 1 1 4 1
0( ) / ; , (1.30)
f a x x x x x
n
2 1 2 3 5 1 4
/ ;
l
2
0 ; (1.31)
f x a x a x a x a b x x x
n
3 4 1 4 2 4 3 4 5 1 4 4 1
;
l
3
0 . (1.32)
Два следующих уравнения (1.33) и (1.34) отвечают извест-
ным заданным результатам интегрирования уравнения (1.1) в
интервалах изменения переменной
t
соответственно от
x
2
до
x
3
и от
a
1
до
x
2 .
f t dt C
x
x
x
x
4 4
3
2
2
3
( ) ln , (1.33)
где
( ) ( )
*
t t
C
t
4
;
*
( )
( )( )( )( )
( )( )
t
t a t x t x t x
t t x t x
1 2 3 5
1 4
;
C
a x x x
x x
4
1 2 3 5
1 4
0 0 ; ( ) ;
l b b
n
4 3 2
( ) .
f t dt C
x x
a x
a
x
5 1 5
2 1
1 1
1
2
( ) ln , (1.34)

37
где
1
5
1
( ) ( )
*
t t
C
t x
;
C
x a x x x x x x
x x x
5
1 1 1 2 1 3 1 5
1 1 4
( )( )( )( )
( )
;
1 1 5
0 0( ) ;
x l
.
Решение полученных уравнений (1.30)—(1.34) примени-
тельно к исходным данным предыдущего примера с конеч-
ной глубиной пазов приведено последней строке табл. 1.1.
Видим, что найденные значения постоянных при достаточно
глубоких пазах (начиная примерно
h
b
2 5, ) практически не
отличаются от их значений при бесконечных глубоких пазах.
Для последнего варианта (
n
*
7
) время счета постоян-
ных комбинированным методом (методом интегрирования
уравнения (1.11) и уточнения его решения итерационным
методом Ньютона) на ЭВМ ЕС—1022 составило около 8 ми-
нут.
1.2.3. Постоянные замкнутого многоугольника
В предыдущем случае, когда многоугольники незамкнуты
в бесконечно удаленных точках (в двух или более), расчет
постоянных может облегчен путем оценки магнитной прово-
димости зазора потоку униполярного намагничивания [151].
Этот поток создается проводниками с током, помещенными
в бесконечно удаленные точки магнитного зазора, одной из
которых при конформном отображении будет соответство-
вать начало координат плоскости
t
. При наличии предвари-
тельных сведений о значениях постоянных точное решение
системы (1.6) может быть найдено методом Ньютона. В рас-
сматриваемом случае получение предварительной информа-
ции о постоянных отмеченным образом исключается и ре-
шение исходной системы (1.6) (включая и расчет модуля по-
стоянной
Ñ
) может быть достаточно надежно реализовано
методом продолжения решения по параметру, когда исход-
ная система уравнений представляется в форме (1.7).
38
В качестве примера рассмотрим отображение верхней по-
луплоскости на 11-угольную область (рис. 1.3), которая соот-
ветствует участку магнитной цепи синхронного двигателя с
постоянными тангенциально намагниченными магнитами
[235].
Примем
a
1
10 ;
a
5
0
;
a
11
;
x
T
x x x a a a a a a a a C
1 2 9 2 3 4
6
7 8 9 10
.
Рис. 1.3. Конформное отображение закрытой многоугольной области
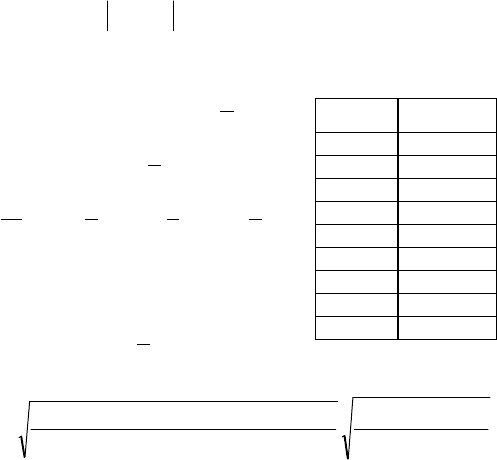
39
Обозначим длины сторон многоугольника:
A A l j
j j j
1
1 2 9( , ,..., ) .
Для указанной области имеем:
1 2 4 8 9
1
2
;
5
6
3
2
;
3
11
8
;
7
9
8
;
10
3
8
;
11
5
8
.
Из формул (1.2), (1.4) следует
arg
C
3
8
;
( )
( )
( )( )( )( )( )
( ) ( )
( )
t
t t x
t a t x t x t x t x
t x t x
t x
4
1 1 3
6
7
2
3
5
8
5
8
.
Исходную систему уравнений, представленную в форме
(1.7), оказалось удобней (по времени счета) решать итераци-
онным методом по формуле (1.12), не прибегая к интегриро-
ванию уравнения (1.11). В табл. 1.3 представлены результаты
расчета.
Здесь вторая строка содержит начальные значения пере-
менных при
0
, а нижняя срока — значения этих пере-
менных при
Т 1
— т. е. искомое решение .
Начальные значения были выбраны произвольно (произ-
вольность выбора ограничивалась только следующими из-
вестными данными: все неизвестные больше
a
1
10 ;
x x j x j x
j j j j
1
1 2 8 0 1 2 3 0( , ,..., ); ( , , ); ;
j
4 5 8, ,..., )) .
Òаблица 1.2
j
l
j
,м
1 0,0015
2 0,003
3 0,0385
4 0,002
5 0,0015
6 0,011
7 0,01
8 0,0004
9 0,0269

40
Начальные шаги в
движении по
были
сравнительно малыми
(10
—3
), на последующих
участках интервала (1.8)
сходимость итераций в
уравнении (1.12) обес-
печивалась и при отно-
сительно больших ша-
гах (вплоть до 0,1). Вре-
мя счета постоянных
составило 90 мин.
Выводы
1. Разработана мето-
дика расчета постоян-
ных Кристоффеля-Шварца, основанная на приведении ис-
ходной системы нелинейных уравнений к эквивалентной
системе с искусственно введенным параметром, которая мо-
жет быть дополнительно преобразована в систему обыкно-
венных дифференциальных уравнений. Обе новых системы
могут быть решены средствами стандартного математическо-
го обеспечения ЭВМ.
2. Определенные интегралы в исходных уравнениях от
функции с разрывами типа бесконечности представлены в
виде суммы из двух интегралов, из которых первый (с по-
дынтегральной функцией, не содержащей разрыва) находит-
ся численным методом, а второй (с разрывной функцией) —
аналитически.
1.3. Магнитное поле в воздушном зазоре электрической
машины при униполярном намагничивании сердечников
1.3.1. Общие особенности расчета магнитного поля
Будем рассматривать магнитное поле при униполярном
намагничивании двух ферромагнитных сердечников с беско-
нечно большой магнитной проницаемостью, разделенных
Пере-
менные
0
T
= 1
x
1
6 9,9998
x
2
3 9,9923
x
3
1 0,1751
x
4
0,5 0,3043
x
5
2 0,4528
x
6
4 0,4532
x
7
16 0,4532
x
8
64 1,575
x
9
10
4
0,0588
Òаблица 1.3
