Архіпова О.С. Вища математика
Подождите немного. Документ загружается.


- 230 -
Y
π
0
π
3
π
X
Рис
. 11.4
Розв
’
язання
.
Обчислимо
коефіцієнти
Фур
'
є
:
( )
∫ ∫ ∫
π
π
−
π
−
π
π=
π
+−
π
=
π
=
0
0
2
2
0
,
6
511
)(
1
dxxdxxdxxfa
∫ ∫ ∫
π
π− π−
π
π
+−
π
=
π
=
0
0
2
cos
1
cos
1
cos)(
1
kxdxxkxdxxkxdxxfa
k
.
Маємо
:
∫∫
π−
π−
π−
=−=
=
=
==
=
0
0
0
sin
1
sin
sin
1
coscos kxdx
k
kx
k
x
kx
k
v
kxdxdv
dxduxu
kxdxx
( )
;
11
cos
1
2
0
2
k
kx
k
k
+−−
==
π−
∫∫
π
π
π
=−=
=
=
==
=
0
0
2
0
2
2
sin
2
sin
sin
1
cos
2
cos kxdxx
k
kx
k
x
kx
k
v
kxdxdv
xdxduxu
kxdxx
=
+−−=
−=
=
==
=
∫
π
π
0
0
cos
1cos2
cos
sin
kxdx
kk
kx
x
k
k
kx
v
kxdxdv
dxduxu
( )
( )
.1
2
sin
112
2
0
2
k
k
k
kx
k
kk
−
π
=
+
π−−
−=
π
Виходить
:
( )
( )
( )
.
113
1
2111
222
kkk
a
k
k
k
k
π
−−
=
−+
−−
π
=
- 231 -
Аналогічно
:
(
)
32
0
0
2
1)1(2
sin
1
sin
1
sin)(
1
k
kxdxxkxdxxkxdxxfb
k
k
π
−−
=
π
+−
π
=
π
=
∫ ∫ ∫
π
π− π−
π
,
тобто
π
−
=
непарне.якщо,
4
парнеякщо,0
32
k
k
k
b
k
Отже, розкладання функції в ряд Фур'є має вигляд
∑
∞
=
−
−π
−
π
−−
+π=
1
222
.)12sin(
)12(
4
cos
1)1(3
12
5
)(
k
k
xk
k
kx
k
xf
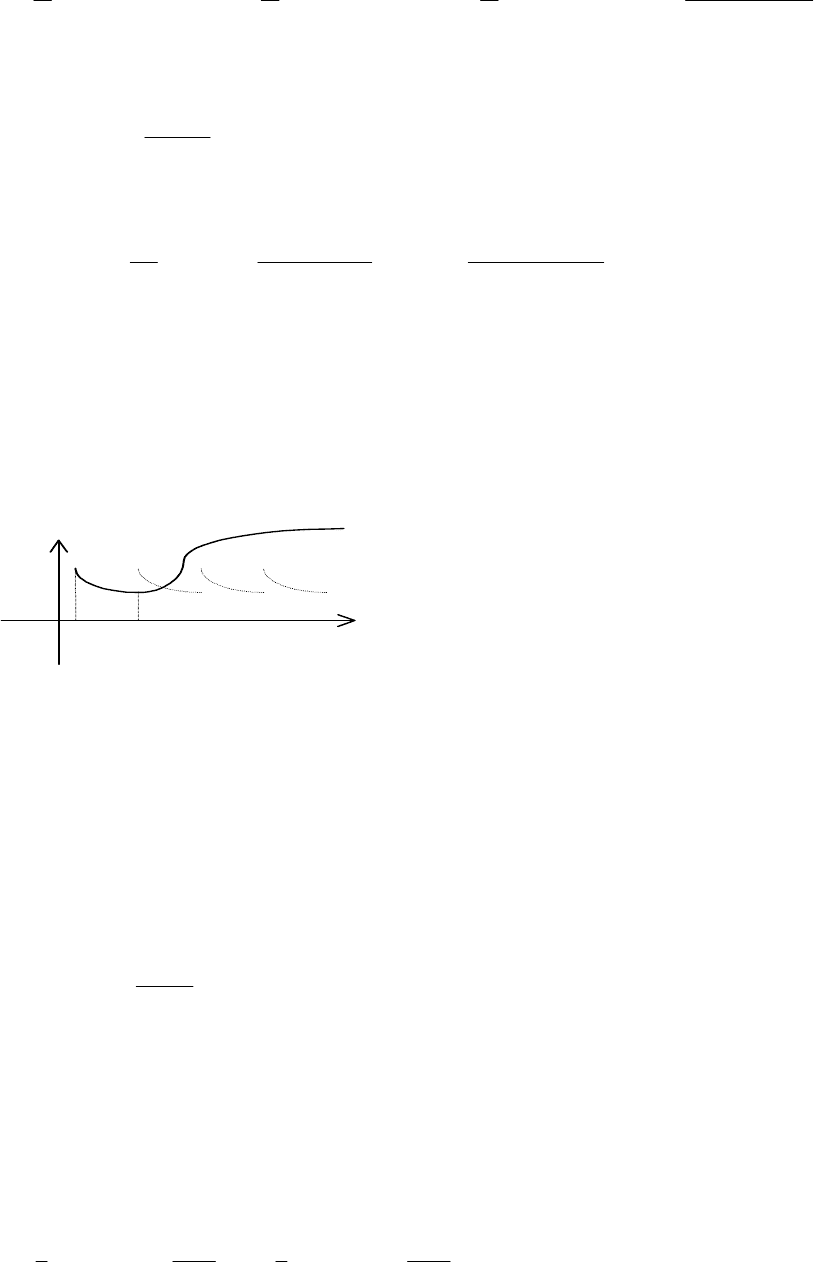
11.5.3. Періодичне продовження і розкладання в ряд Фур'є
неперіодичної функції
Нехай неперіодична функція
(
)
xf , графік якої наведено на рис. 11.5
суцільною лінією, цікавить нас лише на інтервалі
(
)
ba, .
Y
y = f(x )
y = F (x )
0 a b X
Рис. 11.5
Побудуємо періодичну функцію
(
)
xF із періодом
a
b
T
−
≥
, що
збігається з
(
)
xf на відрізку
[
]
ba, . Геометрично для цього потрібно виконати
перенесення графіка функції
(
)
xf паралельно осі OX праворуч і ліворуч на
відстані
,...
,...,
2
,
nT
T
T
(рис. 11.5). Цей процес називається періодичним
продовженням функції
(
)
xf за межі відрізка
b
T
a
x
a
=
+
≤
≤
з періодом
a
b
T
−
=
,
2
ab
l
−
= .
Якщо
(
)
xf задовольняє умови теореми Діріхле, то і
(
)
xF їх теж
задовольняє і, отже, може бути подана у вигляді ряду Фур'є. Через збіг
(
)
xf
та
(
)
xF на
[
]
ba, отриманий ряд і буде рядом Фур'є неперіодичної функції
(
)
xf ,
[
]
bax ,
∈
∀
.
У точках неперервності функції
(
)
xF маємо:
∫ ∫
−
π
=
π
=
l
l
b
a
k
dx
l
xk
xf
l
dx
l
xk
xF
l
a ,cos)(
1
cos)(
1
- 232 -
( )
∫
−
==
π
=
b
a
k
ab
lkdx
l
xk
xf
l
b ,
2
,,2,1sin)(
1
K
( )
.sincos
2
)(
1
0
,
∑
∞
=
π
+
π
+=
k
kk
ba
l
xk
b
l
xk
a
a
xf
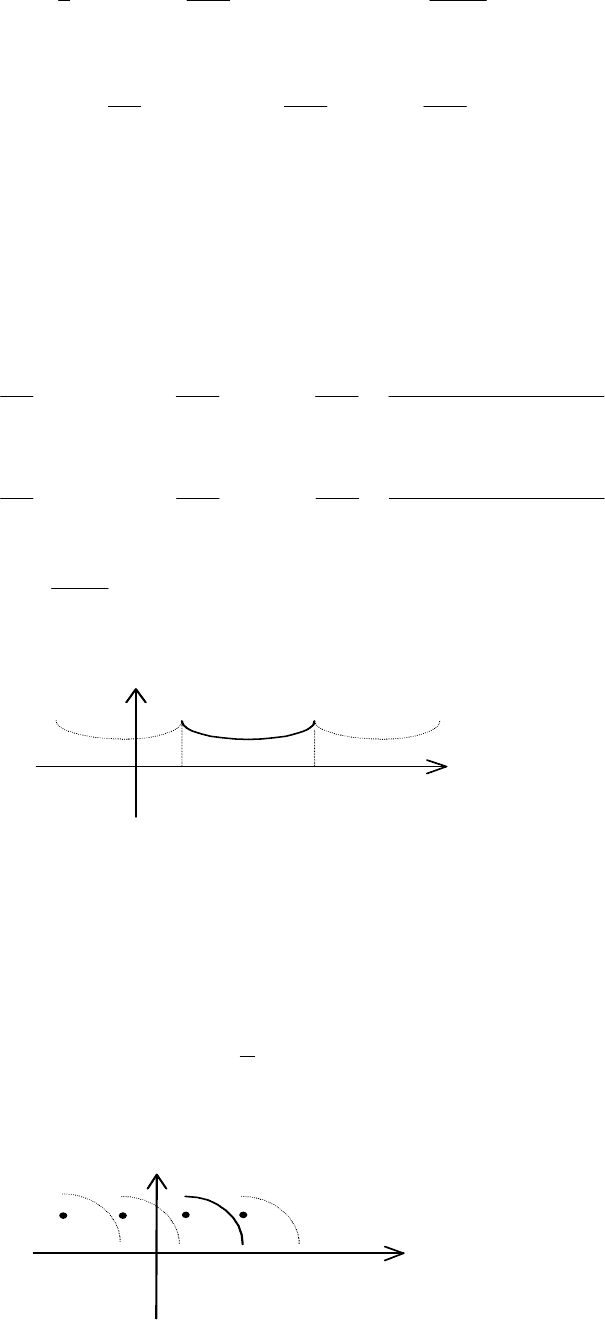
При цьому, якщо
(
)
(
)
bfaf
=
, на кінцях інтервалу
(
)
ba, періодично
продовжена функція
(
)
xF розривів не має (рис. 11.6).
У точках розриву
(
)
xf усередині інтервалу
(
)
ba, і на кінцях інтервалу
(
якщо
(
)
(
)
bfaf
≠
) сума ряду дорівнює півсумі односторонніх границь
функції
(
)
xf , тобто
∑
∞
=
−++
=
π
+
π
+
1
0
;
2
)0()0(
sincos
2
k
kk
xfxf
l
xk
b
l
xk
a
a
при
)
,
(
b
a
x
∈
;
∑
∞
=
−++
=
π
+
π
+
1
0
;
2
)0()0(
sincos
2
k
kk
bfaf
l
xk
b
l
xk
a
a
при
b
x
a
x
=
=
;
,
−
=
2
ab
l .
Y
у = F (x )
0 a b X
Рис. 11.6
Якщо
(
)
(
)
bfaf
≠
, на кінцях інтервалу
(
)
ba, маємо розриви 1-го роду;
оскільки функція
(
)
xF – періодична, за її значення в точках розриву
a
і
b
можна взяти однакові значення, які дорівнюють середньому арифметичному
граничних значень
(
)
)0()0(
2
1
−++ bfaf , що збігається з сумою ряду Фур'є
(
рис. 11.7).
у = F (x)
0 a b X
Рис. 11.7
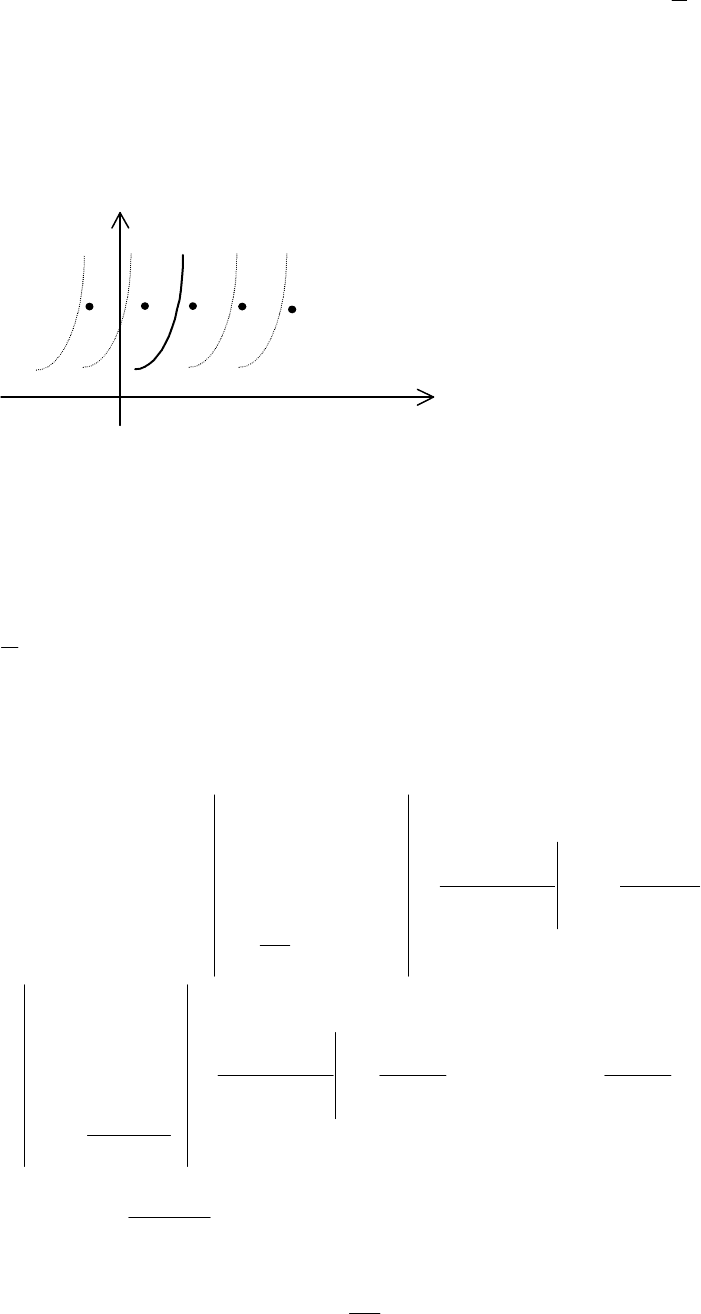
- 233 -
Вважаючи також у точках розриву
(
)
xf значення функції рівним
середньому арифметичному граничних значень
(
)
)0()0(
2
1
−++ xfxf ,
одержуємо, що періодична функція
(
)
xF – це сума ряду Фур'є, що збігається
з
(
)
xf на
[
]
ba, . Графік суми ряду Фур'є є сукупністю кривих та ізольованих
точок.
Приклад. Зобразити
2
)( xxf = рядом Фур'є в (1; 3) (рис. 11.8).
Y y = F(x)
9
5
1
-3 -1 0 1 3 5 X
Рис. 11.8
Розв’язання. Період
1
,
2
1
3
2
=
=
−
=
=
l
l
T
; у точках розриву
(
)
,...2,1,0,12
=
+
=
kkx сума тригонометричного ряду дорівнює
5)31(
2
1
22
=+ , що можна прийняти і як значення функції
(
)
xF .
Знаходимо:
∫
=π=
3
1
cos)( xdxkxfa
k
∫∫
=
π
π
−
π
π
=
π
π
=
π=
==
=π=
3
1
3
1
2
3
1
2
2
2
1
2
xdx
k
xk
k
xkx
xk
k
v
xdxkdv
xdxduxu
xdxkx
sinsin
sin
coscos
−⋅π
π
=π
π
+
π
π
=
π
π
−=
π=
==
=
∫
3cos3(
)(
2
cos
)(
2
)(
cos2
cos
sin
2
3
1
2
3
1
2
k
k
xdxk
kk
xkx
k
xk
v
xdxkdv
dxduxu
,
)1(4
)cos
22
π
−
=π−
k
k
k
де ,)1(3coscos;0sin3sin
k
kkkk −=π=π=π=π
∫ ∫
===π
3
1
3
1
2
0
.
3
26
;0cos dxxaxdxk
- 234 -
Аналогічно обчислюються коефіцієнти
k
b :
∫
π
−
=π=
3
1
.
)1(
8sin)(
k
xdxkxfb
k
k
Одержимо розкладання в ряд Фур'є:
∑
∞
=
π
π
−
π
π
−+=
1
22
)3;1(
2
.
sin
2
cos
)1(4
3
13
k
k
k
xk
k
xk
x
Скориставшись значенням суми
∑
∞
=
π
=
1
2
2
6
1
k
k
,
одержимо, наприклад, при
1
=
x
суму ряду Фур'є, яка дорівнює 5:
∑
∞
=
=+=
π
⋅
π
+=
π
π−
+=
1
2
222
,5
3
2
3
13
6
4
3
13cos)1(
4
3
13
)1(
k
k
k
k
S
що збігається з середнім арифметичним односторонніх границь:
.5)91(
2
1
3
2
1
2
2
1
=+=
+
==
xx
xx
11.5.4. Розкладання в ряд Фур'є функцій, заданих на відрізку
[
[[
[
]
]]
]
l0,
При практичному використанні рядів Фур'є як проміжок, на якому нас
цікавить поводження функції, зручно взяти
[
]
l,0 , тобто
l
b
a
=
=
,
0
.
Поставимо задачу побудови ряду Фур'є для функції, заданої на
[
]
l,0 .
Поза відрізком
[
]
l,0 поводження функції для нас не має значення.
Таким чином, проміжок
[
]
l,0 можна вважати періодом, проте в цьому
випадку необхідно обчислювати коефіцієнти
k
a і
k
b , тобто будувати повний
ряд Фур'є.
Задачу розкладання в ряд Фур'є можна розв’язати і так: виберемо
довільну функцію на відрізку
[
]
0,l
−
і визначимо на всьому відрізку
[
]
ll,
−
деяку функцію
[
]
[
)
−∈
∈
=
0
0
,),(
,),(
)(
lxxg
lxxf
xF .
Функція
(
)
xF визначена в інтервалі завдовжки
l
2
; розкладається у свій ряд
Фур'є на відрізку
[
]
ll,
−
, за винятком, можливо, точок
0
,
=
±
=
x
l
x
і точок
розриву функцій
(
)
xf і
(
)
xg .
Однак перевага віддається найчастіше парному або непарному
продовженню функції на проміжок
[
)
0,l
−
, коли утворюється розкладання в
неповний ряд Фур'є.
- 235 -
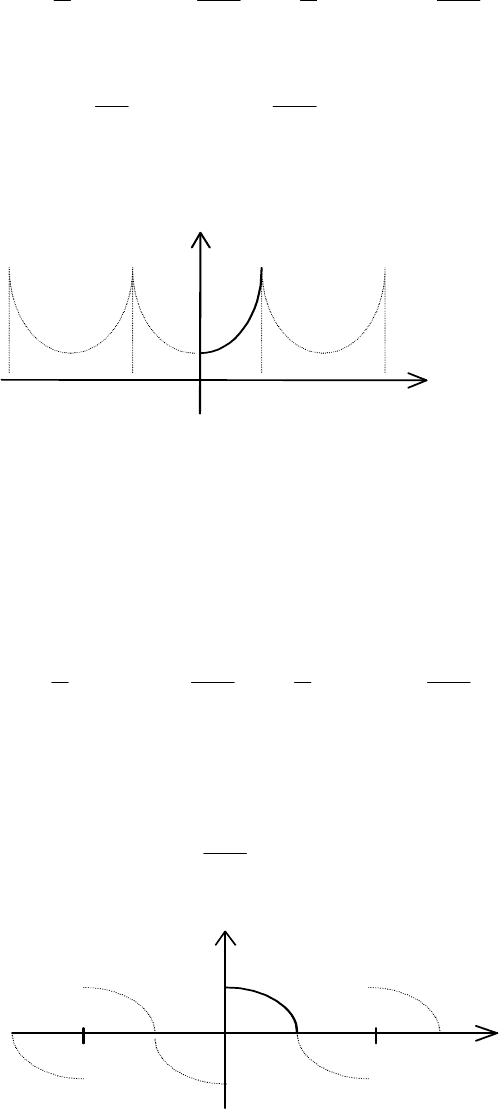
а) Продовжимо функцію парним способом на проміжок
[
)
0,l
−
,
вважаючи
[
]
[
)
−∈−
∈
=
0,),(
,0),(
)(
1
lxxf
lxxf
xf (
рис. 11.9), тоді
(
)
,...2,10
=
=
kb
k
;
∫ ∫
π
=
π
=
l l
k
dx
l
xk
xf
l
dx
l
xk
xf
l
a
0
0
1
cos)(
2
cos)(
2
,
(
)
,...2,1,0
=
k ;
[ ]
∑
∞
=
π
+=
1
0
,0
cos
2
)(
k
k
l
l
xk
a
a
xf .
При
0
=
x
та
l
x
=
даний ряд збігається відповідно до
(
)
00
+
f і до
(
)
0
−
lf .
Y
-3l -l l 3l X
Рис. 11.9
б) При непарному продовженні (рис. 11.10) вважаємо:
[
]
[
)
−∈−−
∈
=
0,),(
,0),(
)(
1
lxxf
lxxf
xf ,
тоді
(
)
,...2,1,00
=
=
ka
k
;
∫ ∫
π
=
π
=
l l
k
dx
l
xk
xf
l
dx
l
xk
xf
l
b
0
0
1
sin)(
2
sin)(
2
,
(
)
,...2,1
=
k .
При непарному продовженні в точках
0
=
x
та
l
x
=
сума тригонометричного
ряду дорівнює 0 і сам ряд має вигляд
[ ]
∑
∞
=
π
=
1
,0
sin)(
k
k
l
l
xk
bxf .
Y
-2 l -l 0 l 2 l 3 l X
Рис. 11.10
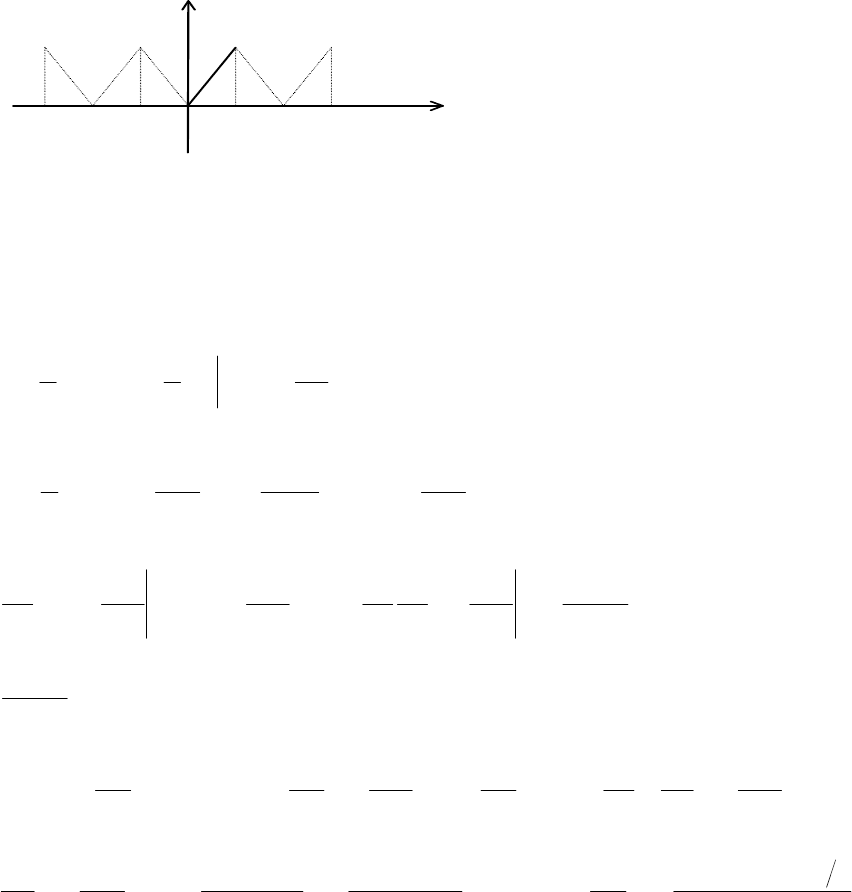
- 236 -
Відзначимо, що при різних аналітичних виразах функції )(
1
xf на
[
)
0,l
−
і на проміжку
(
)
l,0 , ми одержуємо різні аналітичні вирази однієї і тієї
ж функції
(
)
xf : або у вигляді ряду косинусів, або у вигляді ряду синусів, або
у вигляді повного ряду Фур'є.
Теорема. Функцію
(
)
xf , що задана і диференцюється на
(
)
l,0 , можна
нескінченною множиною способів розкласти в тригонометричний ряд.
Можливість вибору продовження функції дозволяє, наприклад,
побудувати ряд, у якому амплітуди гармонік спадають швидше, або ряд,
коефіцієнти якого обчислюються простіше.
Приклад. Розкласти за косинусами функцію
x
x
f
2
)
(
=
, задану на [0,3]
(
рис. 11.11).
Y
6
-9 -6 -3 0 3 6 9 X
Рис. 11.11
Розв’язання. На проміжок [-3,0] функція продовжується парно,
виходить,
(
)
,...2,10
=
=
kb
k
,
3
=
l
, період
6
=
T
. Маємо:
;3
2
;6
3
2
2
3
2
3
0
0
3
0
2
0
∫
====
a
xxdxa
∫ ∫
=
π
⋅π
⋅
=
π
=
3
0
3
0
)
3
(sin
3
43
3
cos2
3
2 xk
xd
k
dx
xk
xa
k
( )
=−π
π
=
π
ππ
=
π
−
π
π
=
∫
1cos
12
3
cos
34
3
sin
3
sin
4
22
3
0
3
0
3
0
k
k
xk
kk
dx
xkxk
x
k
( )
(
)
11
12
22
−−
π
=
k
k
;
[ ]
( )
(
)
∑
∞
=
−
π
−
π
−
π
+=
π
−−
π
+=
1
2222
3;0
3
3
cos
3
2
3
cos2(
12
3
3
cos
1
11
12
32
k
k
xxxk
k
x
( )
( )
( )
( )
∑
∞
=
+
π+
π
−=−
π+
+
−−
π
−
0
2222
.
12
312cos24
3)
3
12
cos
12
2
3
5
cos
5
2
k
k
xkxk
k
x
KK
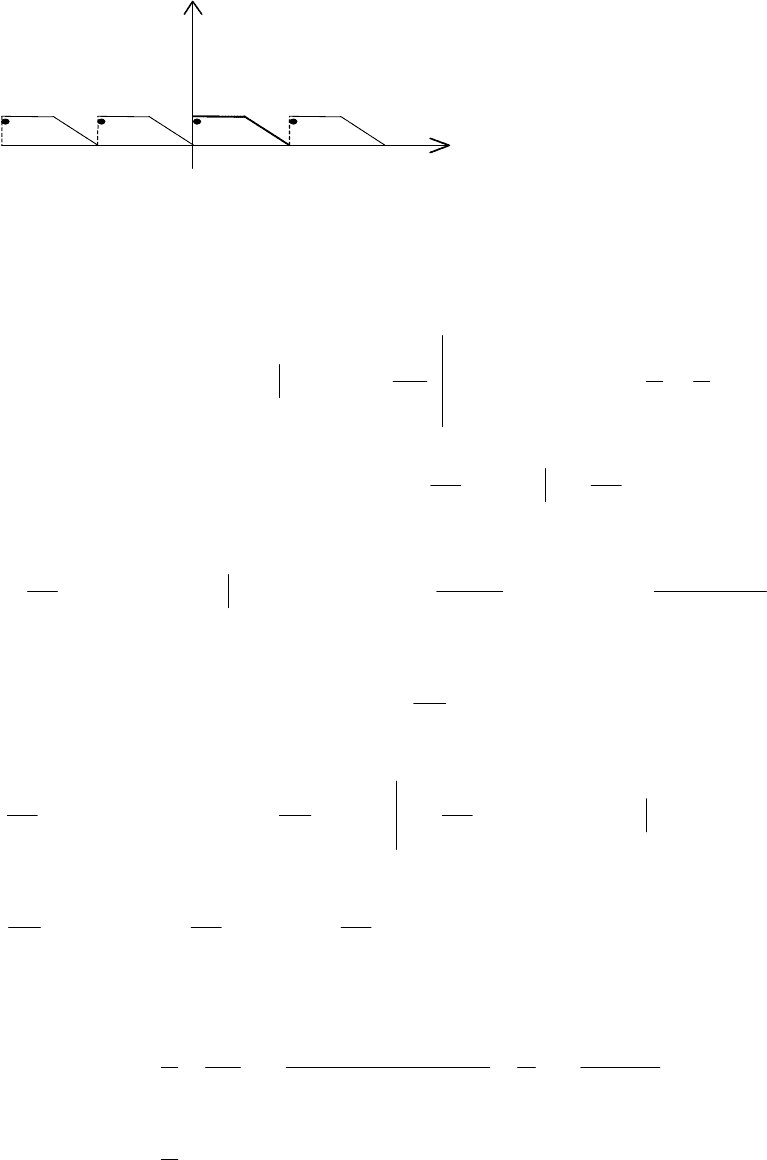
- 237 -
Приклад. Розкласти в ряд Фур'є функцію
[
]
[ ]
∈−
∈
=
2;1,2
1;0,1
)(
xx
x
xf (
рис.
11.12).
Y
1
-4 -2 0 2 4 X
Рис. 11.12
Розв’язання. Маємо:
2
2
,
1
=
=
=
l
T
l
.
( )
∫ ∫
=+−−+=
−+=−+=
1
0
2
1
2
1
2
1
0
0
2
3
2
1
2241
2
22
x
xxdxxdxa ;
( )
=π−
π
−π
π
=π−−π=
∫ ∫ ∫
1
0
2
1
2
1
1
0
)(sin)2(
1
sin
1
cos2cos xkdx
k
xk
k
xdxkxxdxka
k
( ) ( )
( )
(
)
222
2
1
2
1
11
cos1
)(
1
sinsin2
1
π
−−
=π−
π
−
=
π−π−
π
−=
∫
k
k
k
xdxkxkx
k
k
;
( )
∫ ∫ ∫
+π
π
−
=π−−π=
1
0
2
1
1
0
)(cos
1
sin2sin xkd
k
xdxkxxdxkb
k
( )
π−π−
π
+π
π
−
=π−
π
+
∫∫
2
1
2
1
1
0
2
1
coscos2
1
cos
1
)(cos)2(
1
xdxkxkx
k
xk
k
xkdx
k
,
1
)(cos
1
)1(cos
1
π
=π
π
+−π
π
−
=
k
k
k
k
k
де
∫
=π
2
1
0cos xdxk .
Отже,
( )
==
∈
π
π
+
π−−
π
+
=
∑ ∑
∞
=
∞
=
.2;0,
2
1
.2;0,
sin1cos)1)1((1
4
3
)(
1 1
22
xx
x
k
xk
k
xk
xf
k k
k
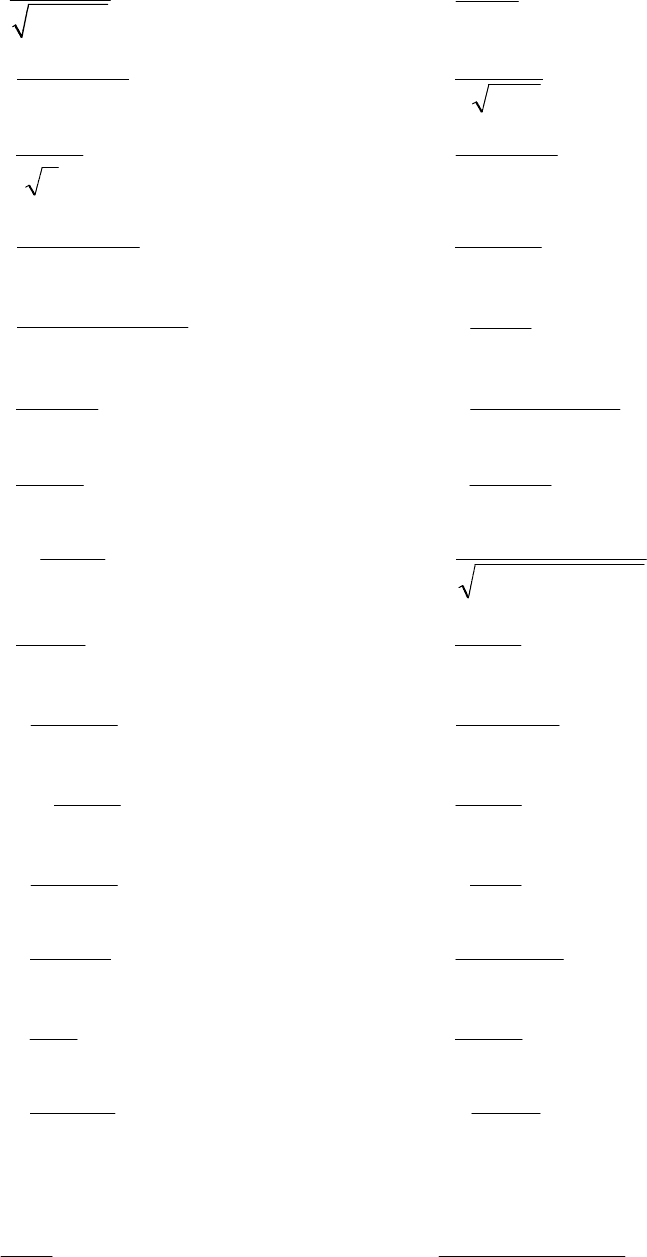
- 238 -
Контрольні
завдання
до
розділу
11
Завдання
1.
Дослідити
збіжність
числових
рядів
:
1
11.1.1.
( 1)
n
u
n n
=
+
;
1
11.1.16.
2 1
n
n
n
u
n
+
=
−
;
)110(
1
.2.1.11
+
=
nn
u
n
;
1
1
.17.1.11
+
=
nn
u
n
;
( )
n
n
n
u
2
12
.3.1.11
−
= ;
2
)12(
1
.18.1.11
−
=
n
u
n
;
1)1(
1
.4.1.11
2
−+
=
n
u
n
;
nn
n
n
u
3
2
.19.1.11
5
+
= ;
)13)(23(
1
.5.1.11
+−
=
nn
u
n
;
n
n
u
n
ln
1
.20.1.11 = ;
1
2
.6.1.11
2
2
+
=
n
n
u
n
;
)3)(2(
1
.21.1.11
++
=
nn
u
n
;
1
.7.1.11
2
+
=
n
n
u
n
;
1
2
1
.22.1.11
2
−
=
n
u
n
;
( )
n
n
n
n
u
1
3
3
.8.1.11
+
= ;
)12)(12(
1
.23.1.11
+−
=
nn
u
n
;
5
6
.9.1.11
−
=
n
n
u
n
;
1
5
2
.24.1.11
+
=
n
n
n
u ;
)1(
12
.10.1.11
+
+
=
nn
n
u
n
;
2
)12(
4
.25.1.11
+
=
n
n
n
u ;
(
)
n
n
n
n
u
1
3
12
.11.1.11
+
+
= ;
n
n
n
u
3
12
.26.1.11
−
= ;
1
2
)1(
.12.1.11
5
+
+
=
n
n
u
n
;
n
n
n
n
u
1
2
.27.1.11
−
= ;
1
2
.13.1.11
3
+
=
n
n
u
n
;
1
1
.28.1.11
2
+
+
+
=
n
n
n
u
n
;
n
n
n
u
2
1
.14.1.11 = ;
1
5
12
.29.1.11
+
+
=
n
n
n
u ;
2
3
1
.15.1.11
2
−
=
n
u
n
;
n
n
n
n
u
2
)
1
2
(.30.1.11
−
= .
Завдання
2.
Дослідити
збіжність
числових
рядів
:
11.2.1.
∑
∞
=
+
1
1
!
n
n
n
n
; 11.2.16.
(
)
∑
∞
=
−⋅⋅⋅⋅⋅
1
5
23741
n
n
!n
n
;
- 239 -
11.2.2. !
2
1
ntg
n
n
⋅
π
∑
∞
=
; 11.2.17.
(
)
( )
∑
∞
=
+⋅⋅⋅⋅⋅
+
1
12753
!12
n
n
n
n
;
11.2.3.
(
)
∑
∞
=
+
1
4
3
3
!2
n
n
n
n
; 11.2.18.
(
)
( )
∑
∞
=
+
−⋅⋅⋅⋅⋅
1
!12
13852
n
n
n
;
11.2.4.
(
)
(
)
( )
∑
∞
=
+
+
1
!14
!12
n
n
n
n
; 11.2.19.
∑
∞
=
+
+
1
4
34
1!
n
n
nn
;
11.2.5.
(
)
( )
∑
∞
=
−⋅⋅⋅⋅⋅
+⋅⋅⋅⋅⋅
1
13852
12753
n
n
n
; 11.2.20.
( )
∑
∞
=
+
1
3
!32
10
n
n
n
n
;
11.2.6.
(
)
∑
∞
=
+
+
1
3
12
!22
n
n
n
; 11.2.21.
(
)
( )
∑
∞
=
+⋅⋅⋅⋅⋅
−⋅⋅⋅⋅⋅
1
5314118
12531
n
n
n
;
11.2.7.
( )
∑
∞
=
+
+
+
1
3
21
!2
42
n
n
n
n
; 11.2.22.
( )
∑
∞
=
+
1
!37
3
n
n
n
n
;
11.2.8.
(
)
( )
∑
∞
=
−
1
!13!
!2
n
nn
n
; 11.2.23.
∑
∞
=1
!4
n
n
n
n
n
;
11.2.9.
(
)
( )
∑
∞
=
+
1
!3
!2
n
n
n
; 11.2.24.
(
)
( )
∑
∞
=
+
+
1
1
!2
n
n
n
n
;
11.2.10.
( )
∑
∞
=
+
1
2
1
!
n
n
n
n
; 11.2.25.
(
)
( )
( )
∑
∞
=
+
1
2
!312
!
n
n
n
n
;
11.2.11.
(
)
( )
∑
∞
=
+
1
2
!2
25
n
n
n
n
; 11.2.26.
(
)
( )
∑
∞
=
+
−⋅⋅⋅⋅⋅
1
!322
34951
n
n
n
n
;
11.2.12.
(
)
∑
∞
=
+
1
!23
n
n
n
n
n
; 11.2.27.
( )
∑
∞
=
+
1
2
!13
6
n
n
n
;
11.2.13.
∑
∞
=
+
1
2
3
!
3
n
n
tg
n
n
; 11.2.28.
( )( )
∑
∞
=
+
1
6
1
sin
!12
!
n
n
n
n
;
11.2.14.
(
)
∑
∞
=
⋅
1
!25
!3
n
n
n
n
; 11.2.29.
∑
∞
=1
2
!
2
n
n
n
arctg
;
11.2.15.
(
)
∑
∞
=1
2
2
!
n
n
n
; 11.2.30.
(
)
( )
∑
∞
=
+
+
+
1
32
!2
32
n
n
n
n
.
Завдання
3.
Знайти
інтервал
збіжності
степеневого
ряду
:
11.3.1.
1)12(
)3()1(
++
−−
=
nn
x
u
nn
n
; 11.3.16. ;
!
)1(
3/
n
xn
u
nn
n
+
=
11.3.2.
2
)1(
!3
+
=
n
xn
u
nn
n
; 11.3.17. ;
9
)1(
2
n
n
n
n
x
u
−
=
