Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.

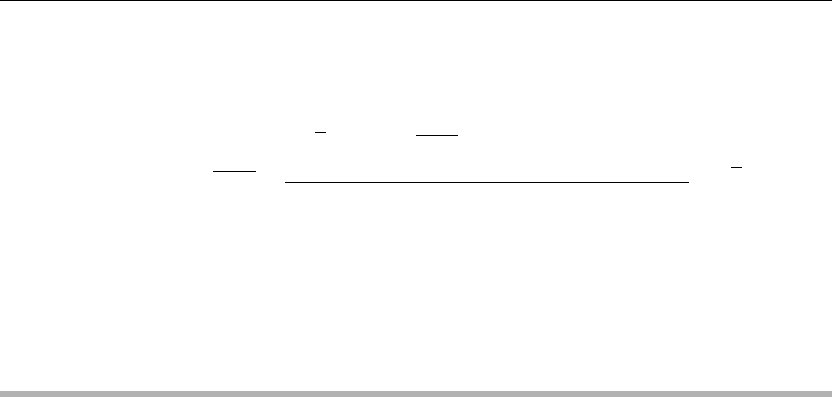
488 Chapter 8
Finally, the solution for the variable portion of the problem is constructed from the super-
position of the products of the time-dependent solutions and the given spatial eigenfunctions,
and this reads
v(x, t) =
∞
n=1
⎛
⎜
⎜
⎜
⎜
⎝
C(n)e
−
n
2
π
2
t
4
+
4
√
2
n
2
π
2
e
−
n
2
π
2
t
4
−n
2
π
2
cos(t) −4 sin(t)
nπ
n
4
π
4
+16
⎞
⎟
⎟
⎟
⎟
⎠
√
2 sin(nπx)
The arbitrary constants C(n) are determined from the initial conditions for the problem.
8.3 Initial Condition Considerations for the
Nonhomogeneous Heat Equation
Substitution of the initial condition into the general solution for the variable portion v(x, t),
from Section 8.2, yields
v(x, 0) = f(x) −s(x, 0)
Substituting the preceding into the following general solution for v(x, t)
v(x, t) =
∞
n=0
⎛
⎝
C(n)e
−kλ
n
t
+
t
0
G1(t, τ)Q
n
(τ)dτ
⎞
⎠
X
n
(x)
at time t = 0 yields
f(x) −s(x, 0) =
∞
n=0
C(n)X
n
(x)
This is the familiar Fourier series expansion of the left-hand side of the equation, and the C(n)
are the Fourier coefficients. Taking the inner product of both sides, with respect to the
orthonormalized eigenfunctions X
n
(x) and the weight function w(x) = 1, and assuming
validity of the interchange between the summation and integration operations, yields
a
0
(
f(x) −s(x, 0)
)
X
m
(x) dx =
∞
n=0
C(n)
⎛
⎝
a
0
X
m
(x)X
n
(x)dx
⎞
⎠
From the statement of orthonormality of the spatial eigenfunctions, the preceding equation
reduces to
a
0
(
f(x) −s(x, 0)
)
X
m
(x)dx =
∞
n=0
C(n)δ(m, n)

Nonhomogeneous Partial Differential Equations 489
Due to the properties of the Kronecker delta function, only one term (m = n) survives this sum,
and the resulting Fourier coefficient reads
C(n) =
a
0
(
f(x) −s(x, 0)
)
X
n
(x)dx (8.2)
Now that we have evaluated the coefficients C(n), we can write the final solution to our
original nonhomogeneous partial differential equation as the sum of the linear portion plus the
transient portion as follows:
u(x, t) =
∞
n=0
⎛
⎝
C(n)e
−kλ
n
t
+
t
0
G1(t, τ)Q
n
(τ)dτ
⎞
⎠
X
n
(x) +s(x, t)
Note that if there is no nonhomogeneous source term h(x, t) in the system, and if the boundary
conditions are time invariant, then the transient portion of the solution v(x, t) goes to zero as t
goes to infinity, and the only remaining term in the solution is the linear term s(x, t). For this
reason, this linear portion of the solution is referred to as the “steady-state” or “equilibrium”
solution to the partial differential equation.
We now demonstrate these concepts for the illustrative problem given in Section 8.2.
DEMONSTRATION: From the given initial condition on the problem, we have
v(x, 0) = f(x) −s(x, 0)
which evaluates to
f(x) −s(x, 0) = x(1 −x)
SOLUTION: The coefficients C(n) are evaluated from the integral
C(n) =
a
0
(
f(x) −s(x, 0)
)
X
n
(x)dx
Substituting the preceding into this integral yields
C(n) =
1
0
x(1 −x)
√
2 sin(nπx)dx
Evaluation of this integral gives
C(n) =−
2
√
2
(−1)
n
−1
n
3
π
3

490 Chapter 8
for n = 1, 2, 3,....Thus, the solution for the variable portion of the problem reads
v(x, t) =
∞
n=1
⎛
⎜
⎝
2
√
2
1 −(−1)
n
e
−
n
2
π
2
t
4
n
3
π
3
+
4
√
2
n
2
π
2
e
−
n
2
π
2
t
4
−n
2
π
2
cos(t) −4 sin(t)
nπ
n
4
π
4
+16
⎞
⎟
⎟
⎟
⎟
⎠
√
2 sin(nπx)
Finally, the solution to our problem is the sum of the linear plus the variable portions evaluated
earlier—that is, u(x, t) = v(x, t) +s(x, t). This yields
u(x, t) =sin(t)(1 −x) +
∞
n=1
⎛
⎜
⎝
2
√
2
1 −(−1)
n
e
−
n
2
π
2
t
4
n
3
π
3
+
4
√
2
n
2
π
2
e
−
n
2
π
2
t
4
−n
2
π
2
cos(t) −4 sin(t)
nπ
n
4
π
4
+16
⎞
⎟
⎟
⎟
⎟
⎠
√
2 sin(nπx)
Note how the solution satisfies the given boundary and initial conditions. The details for the
development of this solution along with the graphics are given later in one of the Maple
worksheet examples.
8.4 Example Nonhomogeneous Problems for the
Diffusion Equation
We now consider solutions to some example nonhomogeneous problems for the heat or
diffusion equation using Maple.
EXAMPLE 8.4.1: We seek the temperature distribution u(x, t) in a thin rod whose lateral
surface is insulated over the interval I ={x |0 <x<1}. The left end of the rod is held at a
fixed temperature of 10, and the right end is held at the fixed temperature of 20. There is no
internal heat source. The thermal diffusivity of the rod is k = 1/20, and the rod has an initial
temperature distribution u(x, 0) = f(x) given as follows.
SOLUTION: The nonhomogeneous diffusion equation is
∂
∂t
u(x, t) = k
∂
2
∂x
2
u(x, t)
+h(x, t)

Nonhomogeneous Partial Differential Equations 491
The boundary conditions are nonhomogeneous type 1 at the left and type 1 at the right:
u(0,t)= 10 and u(1,t)= 20
The initial condition is
u(x, 0) = 60x −50x
2
+10
The internal heat source term is
h(x, t) = 0
The solution is u(x, t) = v(x, t) +s(x, t), where s(x, t) is the linear portion of the solution and
v(x, t) is the variable portion of the solution, which satisfies the partial differential equation
∂
∂t
v(x, t) = k
∂
2
∂x
2
v(x, t)
+q(x, t)
where
q(x, t) = h(x, t) −
∂
∂t
s(x, t)
Assignment of system parameters
> restart: with(plots):a:=1:k:=1/20:h(x,t):=0:
> A(t):=10:B(t):=20:kappa[1]:=1:kappa[2]:=0:kappa[3]:=1:kappa[4]:=0:
> b(t):=(kappa[3]*a*A(t)+A(t)*kappa[4]−B(t)*kappa[2])/(kappa[1]*kappa[3]*a+
kappa[1]*kappa[4]−kappa[2]*kappa[3]);
b(t) := 10 (8.3)
> m(t):=(kappa[1]*B(t)−A(t)*kappa[3])/(kappa[1]*kappa[3]*a+kappa[1]*kappa[4]−
kappa[2]*kappa[3]);
m(t) := 10 (8.4)
Linear portion of solution
> s(x,t):=m(t)*x+b(t);s(x,0):=eval(subs(t=0,s(x,t))):
s(x, t) := 10x +10 (8.5)
By the method of separation of variables, the variable solution is
v(x, t) =
∞
n=0
X
n
(x)T
n
(t)

492 Chapter 8
where T
n
(t) is the solution to the time-dependent differential equation
d
dt
T
n
(t) +kλ
n
T
n
(t) = Q
n
(t)
and X
n
(x) is the solution to the spatial-dependent eigenvalue equation
d
2
dx
2
X
n
(x) +λ
n
X
n
(x) = 0
with boundary conditions
X(0) = 0 and X(1) = 0
The corresponding homogeneous eigenfunction problem consists of the given Euler equation,
along with the homogeneous boundary conditions that are type 1 at the left and type 1 at the
right. The allowed eigenvalues and corresponding orthonormal eigenfunctions are obtained
from Example 2.5.1.
> lambda[n]:=(n*Pi/a)ˆ2;
λ
n
:= n
2
π
2
(8.6)
> X[n](x):=sqrt(2/a)*sin(n*Pi/a*x);X[m](x):=subs(n=m,X[n](x)):
X
n
(x) :=
√
2 sin(nπx) (8.7)
for n = 1, 2, 3,....
Statement of orthonormality with the respective weight function w(x) = 1
> w(x):=1:Int(X[n](x)*X[m](x)*w(x),x=0..a)=delta(n,m);
1
0
2 sin (nπx) sin(mπx)dx = δ(n, m) (8.8)
Time-dependent equation
> diff(T[n](t),t)+k*lambda[n]*T[n](t)=Q[n](t);
d
dt
T
n
(t) +
1
20
n
2
π
2
T
n
(t) = Q
n
(t) (8.9)
> q(x,t):=h(x,t)−diff(s(x,t),t);
q(x, t) := 0 (8.10)
> Q[n](t):=Int(q(x,t)*X[n](x),x=0..a);Q[n](t):=expand(value(%)):
Q
n
(t) :=
1
0
0dx (8.11)
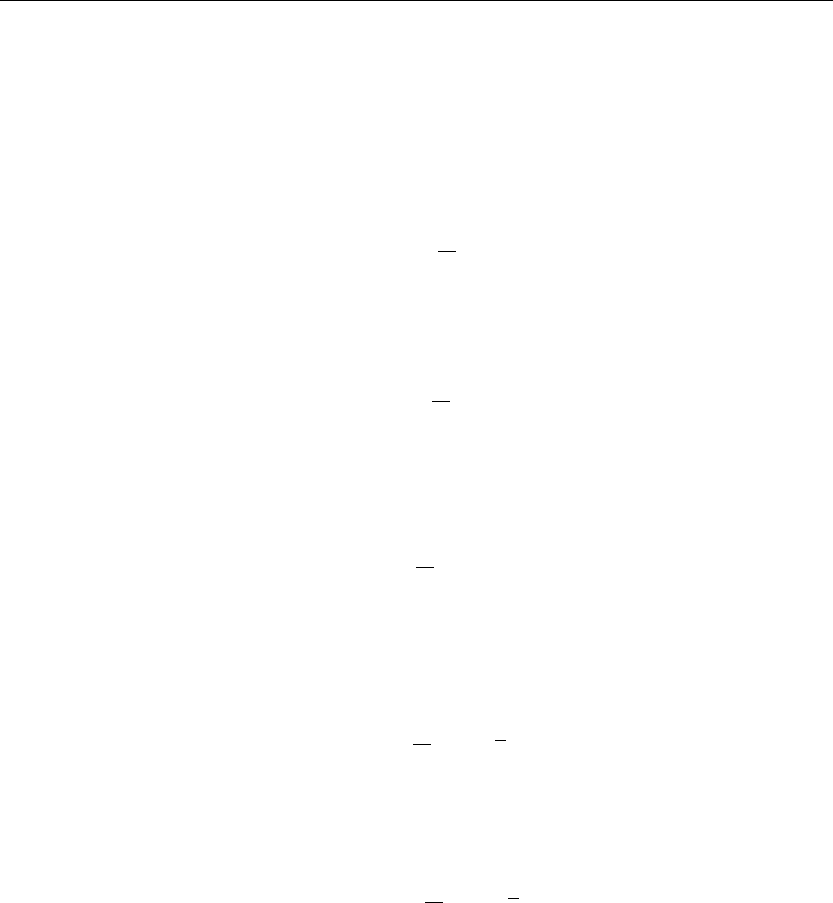
Nonhomogeneous Partial Differential Equations 493
> Q[n](t):=simplify(factor(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},Q[n](t))));
Q[n](tau):=subs(t=tau,%):
Q
n
(t) := 0 (8.12)
Basis vector
> T1(t):=exp(−k*lambda[n]*t);
T 1(t) := e
−
1
20
n
2
π
2
t
(8.13)
First-order Green’s function
> G1(t,tau):=simplify(T1(t)/(subs(t=tau,T1(t))));
G1(t, τ) := e
−
1
20
π
2
n
2
(t−τ)
(8.14)
Time-dependent solution
> T[n](t):=eval(C(n)*T1(t)+Int(G1(t,tau)*Q[n](tau),tau=0..t));T[n](t):=value(%):
T
n
(t) := C(n)e
−
1
20
n
2
π
2
t
+
t
0
0dτ (8.15)
Generalized series terms
> v[n](x,t):=simplify(eval(T[n](t)*X[n](x)));
v
n
(x, t) := C(n)e
−
1
20
n
2
π
2
t
√
2 sin(nπx) (8.16)
Variable portion of solution
> v(x,t):=Sum(v[n](x,t),n=1..infinity);
v(x, t) :=
∞
n=1
C(n)e
−
1
20
n
2
π
2
t
√
2 sin(nπx) (8.17)
The Fourier coefficients C(n) are determined from the integral in Section 8.3 for the special
case where
> f(x):=60*x−50*xˆ2+10;
f(x) := 60x −50x
2
+10 (8.18)
Substituting this into the integral for C(n) yields

494 Chapter 8
> C(n):=Int((f(x)−s(x,0))*X[n](x),x=0..a);C(n):=expand(value(%)):
C(n) :=
1
0
(50x −50x
2
)
√
2 sin(nπx) dx (8.19)
> C(n):=simplify(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},C(n)));
C(n) := −
100
√
2(−1 +(−1)
n
)
n
3
π
3
(8.20)
for n = 1, 2, 3,....
> T[n](t):=(C(n)*T1(t)+int(G1(t,tau)*Q[n](tau),tau=0..t));
T
n
(t) := −
100
√
2(−1 +(−1)
n
)e
−
1
20
n
2
π
2
t
n
3
π
3
(8.21)
Generalized series terms
> v[n](x,t):=simplify(eval(T[n](t)*X[n](x)));
v
n
(x, t) := −
200(−1 +(−1)
n
)e
−
1
20
n
2
π
2
t
sin(nπx)
n
3
π
3
(8.22)
Final solution (linear plus variable portion)
> u(x,t):=eval(Sum(v[n](x,t),n=1..infinity)+s(x,t));
u(x, t) :=
∞
n=1
⎛
⎝
−
200(−1 +(−1)
n
)e
−
1
20
n
2
π
2
t
sin(nπx)
n
3
π
3
⎞
⎠
+10x +10 (8.23)
First few terms of sum
> u(x,t):=s(x,t)+sum(v[n](x,t),n=1..3):
ANIMATION
> animate(u(x,t),x=0..a,t=0..5,thickness=3);
The preceding animation command displays the spatial-time-dependent solution of u(x, t) for
the given boundary conditions and initial conditions. The animation sequence here and in
Figure 8.1 shows snapshots of the animation at times t = 0, 1, 2, 3, 4, 5. Note how the solution
satisfies the given boundary and initial conditions.

Nonhomogeneous Partial Differential Equations 495
ANIMATION SEQUENCE
> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):
> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):
> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):
> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=0..a,thickness=10);
26
24
22
20
18
16
14
12
10
0.2 0.4
x
0.6 0.8 10
Figure 8.1
EXAMPLE 8.4.2: We seek the temperature distribution u(x, t) in a thin rod whose lateral
surface is insulated over the interval I ={x |0 <x<1}. The left end of the rod is up against a
temperature bath with an oscillatory temperature variation, and the right end is held at the fixed
temperature of zero. There is no internal heat source. The thermal diffusivity of the rod is
k = 1/4, and the rod has an initial temperature distribution u(x, 0) = f(x) given as follows.
SOLUTION: The nonhomogeneous diffusion equation is
∂
∂t
u(x, t) = k
∂
2
∂x
2
u(x, t)
+h(x, t)
The boundary conditions are nonhomogeneous type 1 at the left and homogeneous type 1 at the
right:
u(0,t)= sin(t) and u(1,t)= 0
The initial condition is
u(x, 0) = x(1 −x)
The internal heat source term is
h(x, t) = 0

496 Chapter 8
The solution is u(x, t) = v(x, t) +s(x, t), where s(x, t) is the linear portion of the solution and
v(x, t) is the variable portion of the solution, which satisfies the partial differential equation
∂
∂t
v(x, t) = k
∂
2
∂x
2
v(x, t)
+q(x, t)
where
q(x, t) = h(x, t) −
∂
∂t
s(x, t)
Assignment of system parameters
> restart: with(plots):a:=1:k:=1/4:h(x,t):=0:
> A(t):=sin(t):B(t):=0:kappa[1]:=1:kappa[2]:=0:kappa[3]:=1:kappa[4]:=0:
> b(t):=(kappa[3]*a*A(t)+A(t)*kappa[4]−B(t)*kappa[2])/(kappa[1]*kappa[3]*a+kappa[1]*
kappa[4]−kappa[2]*kappa[3]);
b(t) := sin(t) (8.24)
> m(t):=(kappa[1]*B(t)−A(t)*kappa[3])/(kappa[1]*kappa[3]*a+kappa[1]*kappa[4]−
kappa[2]*kappa[3]);
m(t) := −sin(t) (8.25)
Linear portion of solution
> s(x,t):=m(t)*x+b(t);s(x,0):=eval(subs(t=0,s(x,t))):
s(x, t) := −sin(t)x +sin(t) (8.26)
By the method of separation of variables, the variable solution is
v(x, t) =
∞
n=0
X
n
(x)T
n
(t)
where T
n
(t) is the solution to the time-dependent differential equation
d
dt
T
n
(t) +kλ
n
T
n
(t) = Q
n
(t)
and X
n
(x) is the solution to the spatial-dependent eigenvalue equation
d
2
dx
2
X
n
(x) +λ
n
X
n
(x) = 0

Nonhomogeneous Partial Differential Equations 497
with boundary conditions
X(0) = 0 and X(1) = 0
The corresponding homogeneous eigenfunction problem consists of the Euler equation, along
with the homogeneous boundary conditions, which are type 1 at the left and type 1 at the right.
The allowed eigenvalues and corresponding orthonormal eigenfunctions are obtained from
Example 2.5.1.
> lambda[n]:=(n*Pi/a)ˆ2;
λ
n
:= n
2
π
2
(8.27)
> X[n](x):=sqrt(2/a)*sin(n*Pi/a*x);X[m](x):=subs(n=m,X[n](x)):
X
n
(x) :=
√
2 sin(nπx) (8.28)
for n = 1, 2, 3,....
Statement of orthonormality with the respective weight function w(x) = 1
> w(x):=1:Int(X[n](x)*X[m](x)*w(x),x=0..a)=delta(n,m);
1
0
2 sin(nπx) sin(mπx) dx = δ(n, m) (8.29)
Time-dependent equation
> diff(T[n](t),t)+k*lambda[n]*T[n](t)=Q[n](t);
d
dt
T
n
(t) +
1
4
n
2
π
2
T
n
(t) = Q
n
(t) (8.30)
> q(x,t):=h(x,t)−diff(s(x,t),t);
q(x, t) := cos(t)x −cos(t) (8.31)
> Q[n](t):=Int(q(x,t)*X[n](x),x=0..a);Q[n](t):=expand(value(%)):
Q
n
(t) :=
1
0
(cos(t)x −cos(t))
√
2 sin(nπx) dx (8.32)
> Q[n](t):=simplify(factor(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},Q[n](t))));
Q[n](tau):=subs(t=tau,%):
Q
n
(t) := −
√
2 cos(t)
πn
(8.33)
Basis vector
