Arya S.P.S. Introduction to Micrometeorology

Подождите немного. Документ загружается.

148 10 Neutral Boundary Layers

Here,

the neutral

PBL

height is assumed to be proportional to

u*ifwith

estimated coefficient of proportionality of about 0.

.3,

so that h = O..3u*if.

A satisfactory confirmation of Eq. (10.11) and empirical determination

of the similarity functions

and

cannot be made from atmospheric

observations, because a strictly neutral, stationary, and barotropic PBL,

which is not constrained by any inversion from above, is so rare in the

atmosphere that relevant observations

the same do not exist. The

averages

wind profiles measured under slightly unstable and slightly

stable conditions

appear

to follow the above similarity scaling. Some

laboratory simulations of the neutral Ekman layer in a rotating wind tun-

nel flow have also confirmed the same. Of course, there is plenty of

experimental support for the validity of the velocity-defect law [Eq.

(10.10)] in nonrotating flows.

10.2

SURFACE

ROUGHNESS

PARAMETERS

The aerodynamic roughness of a flat and uniform surface may be char-

acterized by the average height

)

of the various roughness elements,

their areal density, characteristic shapes, and dynamic response charac-

teristics (e.g., flexibility and mobility). All the characteristics would be

important, if one were interested in the complex flow field within the

roughness or

canopy

layer. There is not much hope for a generalized and,

at the same time, simple theoretical description of such a three-dimen-

sional flow field in which turbulence dominates

over

the mean motion. In

theoretical and experimental investigations of the fully developed surface

layer, however, the surface roughness is characterized by only one or two

roughness characteristics which can be empirically determined from

wind-profile observations.

The

roughness length

parameter

introduced in Eq. (10.6) is one such

characteristic. In practice,

is determined from the least-square fitting of

Eq.

(10.6) through the wind-profile data, or by graphically plotting In z

versus U

and

extrapolating the best-fitted straight line down to the level

where

U = 0, its intercept on the ordinate axis being In zn. One should

note however, that this is only a mathematical or graphical procedure for

estimating

and that Eq. (10.6) is not expected to describe the actual

wind profile below the tops of roughness elements. An assumption im-

plied in the derivation of

(10.6) is that Zo q z.

Empirical estimates of the roughness parameter for various natural

surfaces can be

ordered

according to the type of terrain (see Fig. 10.5) or

the average height of the roughness elements (see Fig.

10.6). Although

varies

over

five orders of magnitude (from

10-

m for smooth water sur-

10.2 Surface Roughness Parameters 149

*Very

hilly mountainousareas

r:---------------------------,

3:-...

2 )*centers atcities with very toll buildings

*Centers of small towns

*outskirts of towns

I g }*Centers atlargetowns,cities

2 } Many trees, hedges,few buildings

Forests

Fairly level wooded country

10-~

Many hedges

Few

trees ,summer time

Isolated trees

Uncut

grass

Farmland

Long

grass(~60cm),

crops

Airports(runway area)

Fairly level grass plains

Fewtrees, winter time

Cutgrass

(~3cm)

-2

10 9

zo(m) 4

2 Notural snowsurface(farmland)

9 Off-sea wind incoastal areas'

5 Desert(tlat)

3 >Large expanses

water

Calm open sea

41-

Snow-covered

flat

or rolling

ground

.J)

Ice,mud

flats

Heteroae

neous terrain

Fig. 10.5 Typical values, or range of values, of the surface roughness

parameter

for

different types of terrain.

[From

tables by the Royal Aeronautical Society (1972).]

150 10 Neutral

Boundary

Layers

100

.-------r---------.-----~---.,.__---__r--___,

•

log

zo=

-1.24+

1.19

logh

(KUNG,

1961)

--~

0.10

0.01

L£=--

...l.-

---I.

L-

..L..

-L

---l

100

0.01 0.10

1.0

AERODYNAMIC

ROUGHNESS

(m)

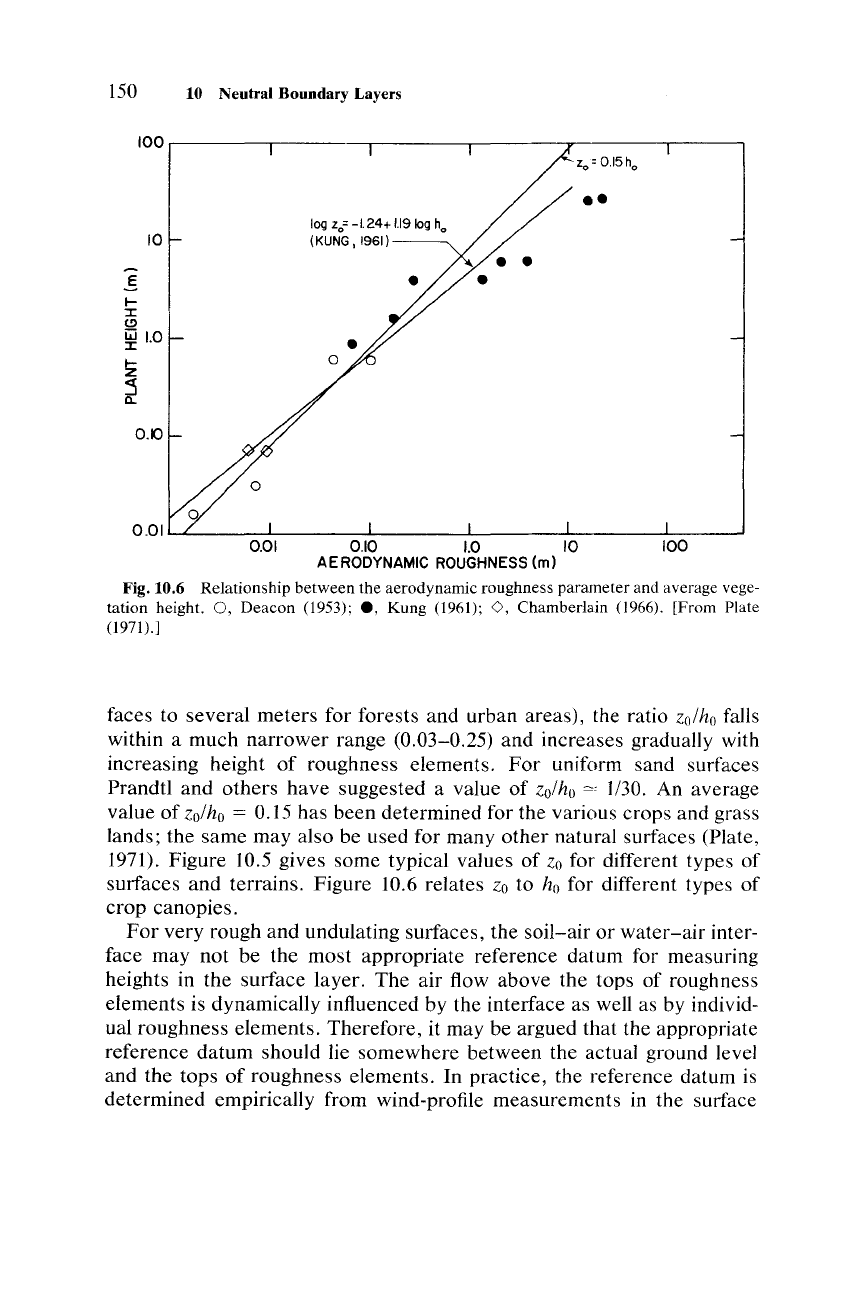
Fig.10.6

Relationship

between

the aerodynamic roughness

parameter

and average vege-

tation height.

Deacon

(1953);

Kung

(1961);

Chamberlain (1966). [From Plate

(1971).]

faces to several meters for forests and urban areas), the ratio

zslh«

falls

within a much

narrower

range (0.03-0.25) and increases gradually with

increasing height of roughness elements.

For

uniform sand surfaces

Prandtl and others have suggested a value of

zo/h

1/30. An average

value of

zo/h

= 0.15 has been determined for the various crops and grass

lands; the same may also be used for many

other

natural surfaces (Plate,

1971). Figure 10.5 gives some typical values of

for different types of

surfaces and terrains. Figure 10.6 relates

zo to h

for different types of

crop

canopies.

For

very rough and undulating surfaces, the

soil-air

water-air

inter-

face may not be the most appropriate reference datum for measuring

heights in the surface layer. The air flow above the tops of roughness

elements is dynamically influenced by the interface as well as by individ-

ual roughness elements. Therefore, it may be argued that the appropriate

reference datum should lie somewhere between the actual ground level

and the tops of roughness elements. In practice, the reference datum is

determined empirically from wind-profile measurements in the surface

10.2 Surface Roughness Parameters 151

,;"

r"'-

loge

=0.9

~Iog

- 3./5

f-/

f-(S

~NHI

L,t

~69

·1

0.02

0.0

0.02 0.05 OJ 0.2 0.5 I 2 5 10 20

VEGETATION HEIGHT

(rn)

Fig. 10.7 Relationship

between

the zero-plane displacement and average vegetation

height for different types of vegetation. [After Stanhill (1969).]

E 10

::E

w 2

..J

w 0.5

0.2

0.05

layer

under

near-neutral stability conditions.

The

modified logarithmic

wind-profile law

used

for this

purpose

Ulu-;

= (Ilk) In(z' -

do)/zo

(10.12)

in which dois called zero-plane displacement or displacement length and

z' is

the

height

measured

above

the ground level.

For

a plane surface, dois

expected

to lie between

zero

and h

depend-

ing on

the

areal density of roughness elements.

The

displacement height

may be

expected

to increase with increasing roughness density and ap-

proach

a value

to h

for

very

dense

canopies in which the flow within

the

canopy

might

become

stagnant, or independent of the air flow above

the

canopy.

These

expectations

are

indeed borne out by empirical esti-

mates

dofor vegetative canopies (see Fig. 10.7) which indicate that the

appropriate

datum

for wind-profile

measurements

over

most vegetative

canopies

is displaced

above

the

ground level by

70-80%

of the average

height

vegetation.

The

zero-plane displacement in an urban boundary

layer

can

similarly be

expected

to be a large fraction of the average

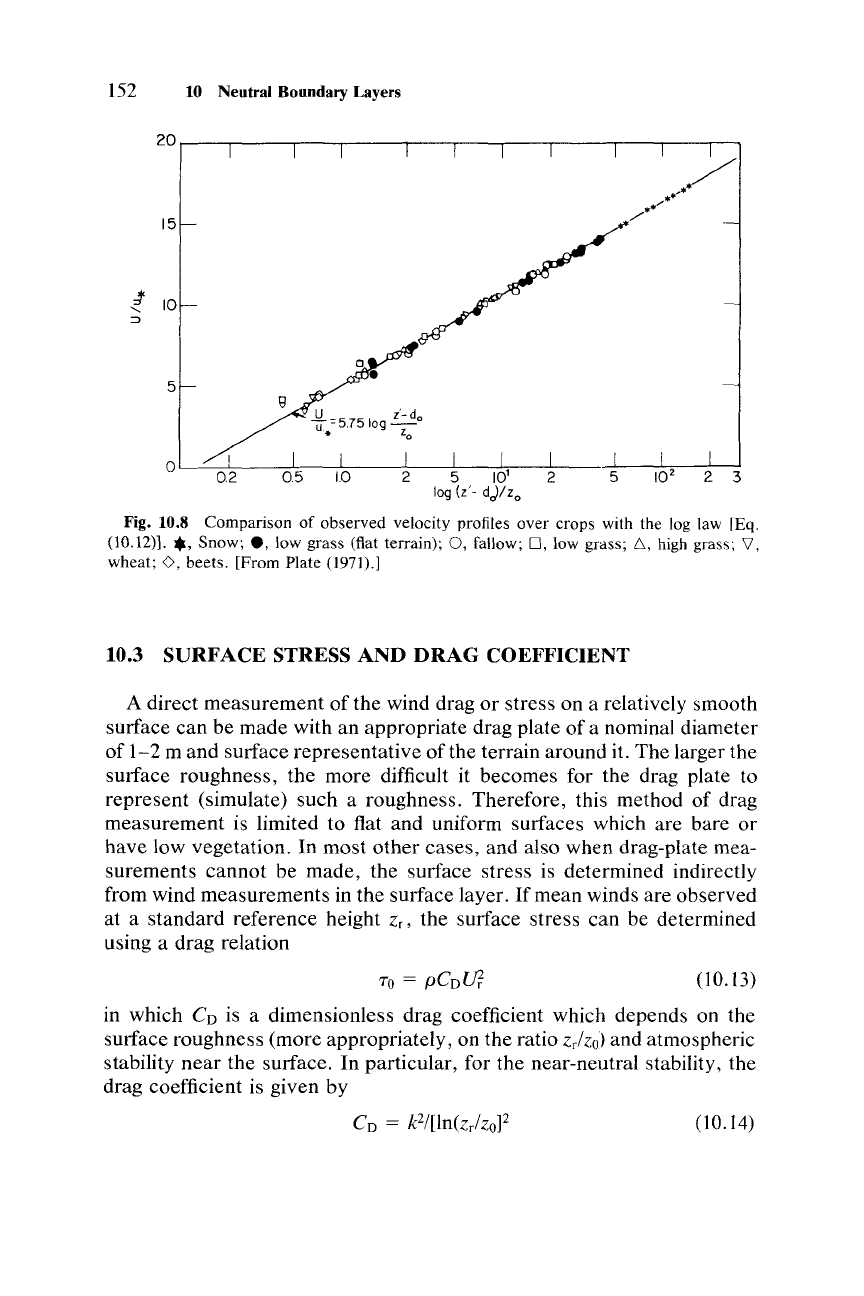
building height. Figure 10.8 shows a verification of

Eq.

(10.12) against

observed

wind profiles

over

vegetative surfaces.

152 10 Neutral Boundary Layers

20....--..,....----,...---r---..,....---...,---,.----r---,----r--,----,

,-"

! 10

:::>

JL=

575

log

u.. Zo

2 5 10' 2

log (z - ddlzo

Fig. 10.8 Comparison of observed velocity profiles over crops with the log law [Eq.

(10.12)] . • , Snow;

low grass (flat terrain);

fallow; D, low grass; L., high grass;

\I,

wheat;

beets. [From Plate (1971).]

10.3

SURFACE

STRESS

AND

DRAG

COEFFICIENT

A direct measurement of the wind drag or stress on a relatively smooth

surface

can

be made with an appropriate drag plate of a nominal diameter

1-2

m and surface representative of the terrain around it. The larger the

surface roughness, the more difficult it becomes for the drag plate to

represent (simulate) such a roughness. Therefore, this method of drag

measurement is limited to flat and uniform surfaces which are bare or

have low vegetation. In most

other

cases, and also when drag-plate mea-

surements cannot be made, the surface stress is determined indirectly

from wind measurements in the surface layer. If mean winds are observed

at a standard reference height

z., the surface stress can be determined

using a drag relation

70 =

pCDlfl

(10.13)

in which CD is a dimensionless drag coefficient which depends on the

surface roughness (more appropriately, on the ratio

zr/zol

and atmospheric

stability

near

the surface. In particular, for the near-neutral stability, the

drag coefficient is given by

(10.14)

10.4 Turbulence 153

which follows from Eqs. (10.6) and (10.13).

Note

that for a given Zr,

increases with increasing surface roughness.

For

a standard reference

height

10 rn, values of CD range from 1.2 x 10-

for large lake and

ocean surfaces at moderate wind speeds

< 6 m sec:") to 7.5 x 10-

for tall

crops

and moderately rough (zo < 0.1 m) surfaces.

For

very rough

surfaces (e.g., forests and urban areas), however, a reference height

m would not be adequate; it must be at least 1.5 times the height of

roughness elements. In some applications the surface geostrophic wind

(Go) or the actual wind speed

at the top of the

PBL

is chosen as the

reference velocity in

Eq.

(10.13).

Equation

(10.13), with prescribed values

CD, is often used for para-

meterizing the surface stress in large-scale atmospheric circulation

models.

Because

specification

eddy viscosity also involves To or us ,

Eq. (10.13)

can

also be used in certain K models of the PBL.

detailed

measurements

wind profile in the surface layer are available from a

micrometeorological mast, u*

under

near-neutral conditions can be deter-

mined from the least-square fitting

Eq. (10.6) to the profile

data

or from

a single graphical plot

In Z versus U.

Note

that

in the latter case, the

slope

the best-fitted straight line must be equal to klu«.

10.4 TURBULENCE

Turbulence in a neutrally stratified boundary layer is entirely

me-

chanical origin and depends on the surface friction and vertical distribu-

tion

wind shear.

From

similarity considerations discussed in Section

10.3, the primary velocity scale is u; and normalized standard deviations

velocity fluctuations

(aju*,

Ju«,

and o-wlu*) must be constants in the

surface

layer

and some functions

the normalized height felu; in the

outer

layer. Surface

layer

observations from different sites indicate that

under

near-neutral conditions

o-ju*

-= 2.5, o-v!u* -= 1.9, and o-,vlu* -= 1.3

(Panofsky and

Dutton,

1984, Chap. 7). Observed values

turbulence

intensity

(o-jV)

are

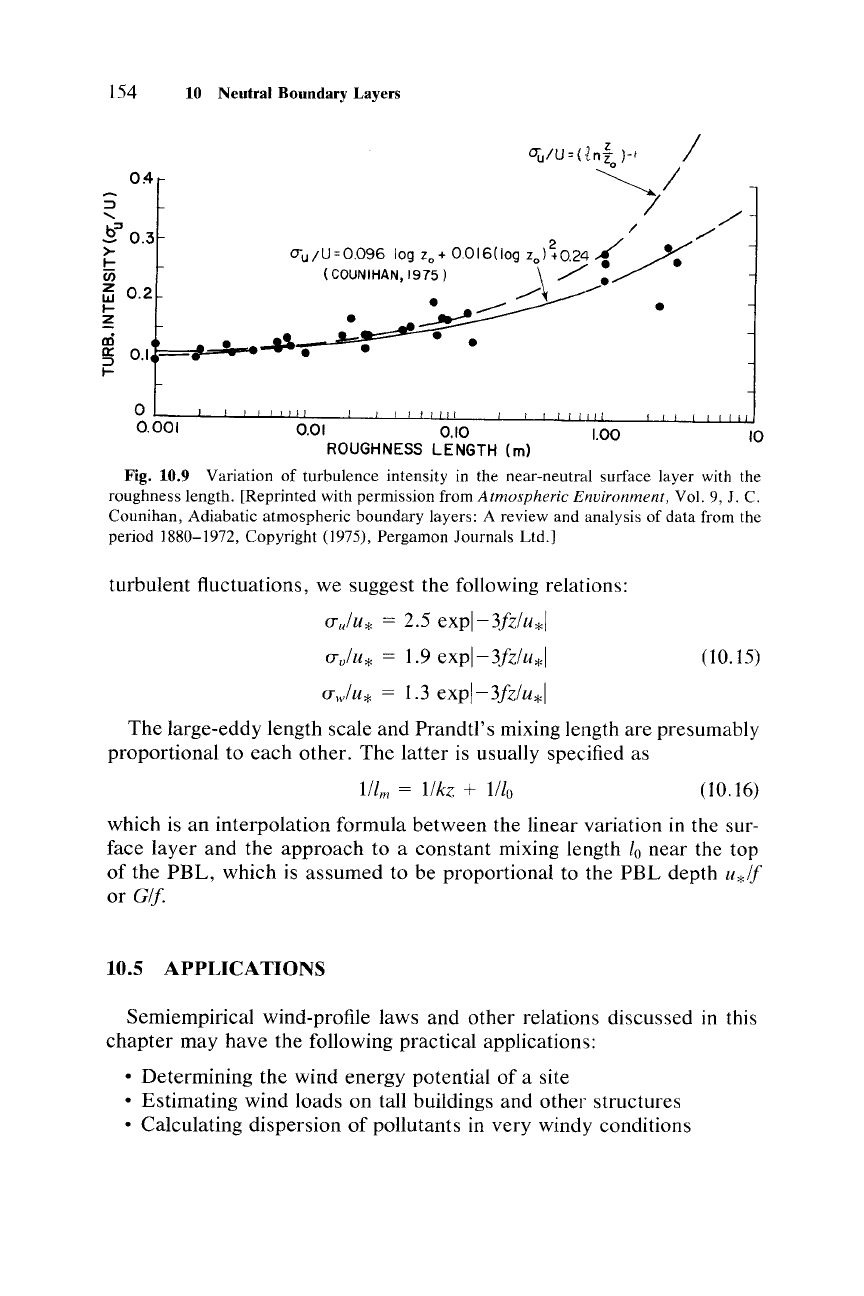
shown

in Fig. 10.9 as function

the roughness

parameter.

These

are

compared with the theoretical relation

a.l

U =

1/In(zlzo), which is

based

o-ju*

= 2.5 and the logarithmic wind-profile

law.

The

above theoretical relation seems to overestimate turbulence

intensities

over

very

rough surfaces. Counihan (1975) has suggested an

alternative empirical relationship between

o-jU

and log

, which pro-

vides a

better

fit to the observed

data

in Fig. 10.9.

Measurements

in the

upper

part

of the neutral

PBL

are lacking, as

pointed

out

earlier,

but

numerical model results indicate approximately

exponential

decrease

o-ju*,

etc.,

with height.

For

rough estimates of

154 10 Neutral Boundary Layers

•

::::l

b'"

0.3

e;;

0.2

I-

a:i

.ll.

0.1l--=-

.....

a.:·

...

-...-·

I-

1.00

0.01 0,10

ROUGHNESS LENGTH

(m)

Fig. 10.9 Variation of turbulence intensity in the near-neutral surface layer with the

roughness length, [Reprinted with permission from

Atmospheric Environment, Vol. 9, J. C.

Counihan, Adiabatic atmospheric boundary layers: A review and analysis of data from the

period

1880-1972, Copyright (1975), Pergamon Journals Ltd.]

(10.15)

turbulent fluctuations, we suggest the following relations:

a.fu

; = 2.5 expl-3!zlu*1

U'v!u*

= 1.9

expl-

3!zlu*1

U'wlu*

= 1.3 expl-3!zlu*1

The large-eddy length scale and Prandtl's mixing length are presumably

proportional to each other. The latter is usually specified as

IIl

lIkz

+ lila (10.16)

which is an interpolation formula between the linear variation in the sur-

face layer and the approach to a constant mixing length

near the top

of the

PBL,

which is assumed to be proportional to the

PBL

depth u*1f

Glf

10.5

APPLICATIONS

Semiempirical wind-profile laws and

other

relations discussed in this

chapter may have the following practical applications:

• Determining the wind energy potential of a site

• Estimating wind loads on tall buildings and other structures

• Calculating dispersion of pollutants in very windy conditions

Problems and Exercises 155

• Characterizing aerodynamic surface roughness

• Parameterizing the surface drag in large-scale atmospheric models, as

well as in wave height and storm surge formulations.

PROBLEMS

AND

EXERCISES

1. Show

that

in the constant-stress surface layer, the power-law wind

profile

[Eq.

(10.2)] implies a power-law eddy viscosity profile [Eq.

(10.3)]

and that the two exponents are related as n =, 1 - m.

2. Derive the logarithmic wind-profile law on the basis of the eddy viscos-

ity and mixing-lengths hypotheses, assuming

= kr, and Ki; = kzu;

in the constant-stress surface layer.

3. Using the logarithmic wind-profile law, plot the expected wind profiles

(using a linear height scale) to a height of

100 m for the following

combinations of the roughness parameter

(zo) and the mean wind speed

at 100 m:

(a)

20 = 0.0] m; U

IOO

= 5, 10, 15, and 20 m

sec

(b) U

IOO

= ]0 m sec

20 = 10-

10-

and]

ill

Also calculate for each profile the friction velocity u; and the drag

coefficient Co for a reference height of 10 m, and show their values on

the graphs.

4. The following mean velocity profiles were measured during the

Wangara Experiment conducted

over

a uniform short-grass surface

= 10 cm)

under

near-neutral stability conditions:

Mean wind speed

(m sec-I)

Height

(m)

Period

Period 2

0.5 7.82

4.91

1 8.66 5.44

9.54

6.06

10.33

6.64

8 11.22

7.17

16 12.01

7.71

(a) Determine the roughness parameter and the surface stress for each

the above observation periods. Take p = J.25 kg

(b)

For

both the periods estimate eddy viscosity, mixing length, and

standard deviation of vertical velocity fluctuations at

20 m.

5. If the

sea

surface behaves like a smooth surface at low wind speeds

156 10 Neutral Boundary Layers

< 2.5 m

sec'),

like a completely rough surface at high wind

speeds

> 7.5 m

sec-I),

and like a transitionally rough surface at

speeds in

between,

express and plot the drag coefficient

as a func-

tion

in the range 0.5

sec-

50, assuming the fol-

lowing:

(a)

= O.13v/u* in the aerodynamically smooth regime

(b)

0.02uVg

the

aerodynamically rough regime

(c)

= 2 X 10-

m in the transitional regime

Chapter 11

Momentum and Heat Exchanges

with Homogeneous Surfaces

11.1

THE

MONIN-OBUKHOV

SIMILARITY

THEORY

In the previous chapter, we showed that the atmospheric surface layer

under neutral conditions is characterized by a logarithmic wind profile

and nearly uniform (with respect to height) profiles of momentum flux and

standard deviations of turbulent velocity fluctuations.

It was also men-

tioned

that

the neutral stability condition is an exception rather than the

rule in the lower atmosphere. More often, the turbulent exchange of heat

between the surface and the atmosphere leads to thermal stratification of

the surface layer and, to some extent, of the whole PBL, as shown in

Chapter 5.

has

been

of considerable interest to micrometeorologists to

find a suitable theoretical or semiempirical framework for a quantitative

description

the mean and turbulence structure of the stratified surface

layer. The

Monin-Obukhov

similarity theory has provided the most suit-

able and acceptable framework for organizing and presenting the micro-

meteorological data, as well as for extrapolating and predicting certain

micrometeorological information where direct measurements of the same

are not available.

1I.1.1

THE

SIMILARITY

HYPOTHESIS

The basic similarity hypothesis first proposed by Monin and Obukhov

(1954) is that in a horizontally homogeneous surface layer the mean flow

and turbulent characteristics depend only on the four independent vari-

ables: the height above the surface z, the friction velocity

U*, the surface

kinematic

heat

flux Ho/pc

and the buoyancy variable g/To (this appears

in the expressions for buoyant acceleration and static stability given ear-

lier). The simplifying assumptions implied in this similarity hypothesis are

that the flow is horizontally homogeneous and quasistationary, the turbu-

lent fluxes

momentum

and

heat are constant (independent of height),

157