Balakumar Balachandran, Magrab E.B. Vibrations

Подождите немного. Документ загружается.

In addition, in Sections 9.3.1 and 9.3.2, we assume that the axial load is ab-

sent and that the elastic foundation is not present; that is,

(9.49)

The boundary conditions simplify accordingly.

The effect of axial load and elastic foundation on the free oscillations of

beams is considered in Section 9.3.3, and beams with varying cross-sections

are considered in Section 9.3.5. In light of the assumptions given by Eqs.

(9.48) and (9.49), Eq. (9.40) reduces to

(9.50)

Equation (9.50), along with the appropriate boundary conditions given by

Eqs. (9.47) or chosen from Table 9.1, represent the governing equations of

a damped beam

subjected to transverse loading. We study the free response

of the undamped system ﬁrst, and then use this as a basis to determine the re-

sponse of the damped system subjected to dynamic forcing in Section 9.4.

Before proceeding to the next section, a few comments about Eq. (9.50)

are in order. This equation is a partial differential equation with a fourth-

order spatial derivative and a second-order time derivative. Since the highest

spatial derivative is fourth order, four boundary conditions are needed. Simi-

larly, since the highest time derivative is second order, two initial conditions

are needed. In the rest of this chapter, it is assumed that appropriate informa-

tion is available to completely deﬁne the response determined as a solution of

Eq. (9.50).

EXAMPLE 9.1

Boundary conditions for a cantilever beam with an extended mass

Consider a uniform cantilever beam that has an extended rigid mass M

at-

tached to its free end as shown in Figure 9.6. Comparing this system to the

system shown in Case 9 in Table 9.1, we note the mass center is located away

from x  L and the discrete springs are attached away from x  L. The

mass has a mass moment of inertia J

about its center of mass. In addition,

a linear spring with stiffness k

is attached to the free end of the mass and

a torsion spring with stiffness k

is attached to the center of the mass. In

 rA

 f 1x,t 2

p1x,t 2 0

and

 0

560 CHAPTER 9 Vibrations of Beams

Although the beam interior is undamped, due to the presence of damping elements at the

boundaries, the beam system is considered a damped system.

D. Zhou, “The vibrations of a cantilever beam carrying a heavy tip mass with elastic supports,”

J. Sound Vibration, Vol. 206, No. 2, pp. 275–279 (1997); H. Seidel and L. Csepregi, “Design

optimization for cantilever-type accelerometers,” Sensors and Actuators, Vol. 6, pp. 81–92

(1984); C. L. Kirk and S. M. Wiedemann, “Natural Frequencies and Mode Shapes of a Free-Free

Beam with Large End Mass,” J. Sound Vibration, Vol. 254, No. 5, pp. 939–949, 2002.

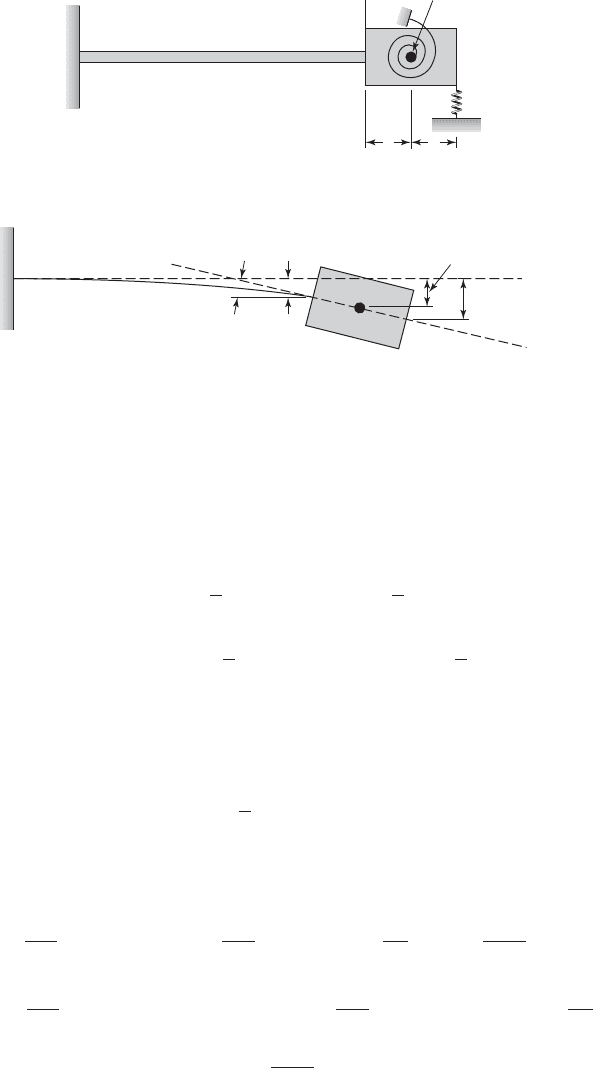
Figure 9.6b, the transverse displacements are shown at several locations on

the extended mass. With this information, we shall obtain an expression for

the discrete Lagrangian G

at the right end of the beam. Using Eq. (9.21) as a

guide, we obtain the following expression for G

at x  L

(a)

where the prime denotes the derivative with respect to x and the overdot de-

notes the derivative with respect to time. For the system of Figure 9.6, the

function G

is obtained from Eq. (9.19) by setting k

 p  f

 0; that is,

(b)

Upon substituting Eqs. (a) and (b) into Eqs. (9.30b) and (9.31b) and per-

forming the indicated operations, we obtain, respectively,

(c)

 1J

 M

0x0t

xL

ck

 d

2w  M

 Ak

 k

 d

xL

 ck

w  M

 1d

 d

 M

0x0t

xL

1x,t,w,w

,w¿,w

¿,w– 2

3rAw

 EIw–



 3d

 d

4w¿



w¿

1t,w

,w¿

2

 d



9.2 Governing Equations of Motion 561

x  0

x  L

 d

w

(d

 d

)w

w

, J

Center of mass

(a)

(b)

FIGURE 9.6

(a) Cantilever beam with an

extended mass attached to its free

end and (b) displacement at several

locations on the extended mass.

When d

 d

 0, Eqs. (c) reduce to those given by Eqs. (9.47b) with p  c

 0. The other two boundary conditions are given by the ﬁrst entry of Table 9.1.

9.3 FREE OSCILLATIONS: NATURAL FREQUENCIES AND MODE SHAPES

9.3.1 Introduction

In this section, free oscillations of undamped, homogeneous and uniform

beams are examined in detail. To this end, we use Eqs. (9.50) and (9.41b) and

set the external nonconservative loading f

(x,t) to zero and obtain the fol-

lowing governing equation of the beam for 0  x  L:

(9.51)

In order to keep the discussion general in terms of boundary conditions, we

consider the system shown in Figure 9.7. We place a translation spring with

constant k

and a torsion spring with constant k

at x  0 and place a transla-

tion spring with constant k

and a torsion spring with constant k

at x  L. In

addition, at x  L there is a rigid body with a mass M

that has a mass mo-

ment of inertia J

. Then, from Eqs. (9.47a) with p  c

 M

 J

 0, the

boundary conditions at x  0 are

(9.52a)

From Eqs. (9.47a) with p  c

 0, M

 M

, J

 J

, the boundary condi-

tions at x  L are

(9.52b)

In writing Eqs. (9.52), we have employed the compact notation that

w

x0

 w10,t 2,

x0

 w¿10,t2,

x0

 w–10,t2,

EIw‡1L,t 2 k

w1L,t 2 M

1L,t 2

EIw–1L,t 2k

w¿1L,t 2J

¿1L,t 2

EIw‡10,t 2k

w10,t 2

EIw–10,t 2 k

w¿10,t 2

 rA

 rAg

562 CHAPTER 9 Vibrations of Beams

x  0 x  L

, J

FIGURE 9.7

Beam with spring elements at left

and right boundaries and an inertia

element at the right boundary.

9.3 Free Oscillations 563

and so on. In addition, we have used the fact that EI is constant.

For a given set of initial conditions, the response of the beam governed

by Eqs. (9.51) and (9.52) is expressed as

(9.53)

where w

(x) is the static response or the static-equilibrium position and

dyn

(x,t) is the displacement measured from the static-equilibrium position.

The static-equilibrium position satisﬁes the static-equilibrium equation

(9.54)

and the following boundary conditions at x  0

(9.55a)

and the following boundary conditions at x  L

(9.55b)

Although the solution of Eq. (9.54) subject to the boundary conditions

Eqs. (9.55) can be found, this is not explicitly carried out here. Nevertheless,

the droop of a beam due to its own weight is given by w

(x). Any constant

loading acting on a distributed-parameter system will inﬂuence the static-

equilibrium position of that system. For most commonly used structural

materials and geometries, the static deformation w

(x) due to gravity and

other static loading is assumed to be small in magnitude and this deformation

is often ignored in the analysis. However, there are cases such as an aircraft

wing, where the static deformation is pronounced and cannot be ignored.

In MEMS, residual stresses due to the fabrication process can lead to a static

deformation.

In Sections 3.2 and 7.2, it was shown the static-equilibrium position of a

single degree-of-freedom system is determined by solving an algebraic equa-

tion and the static-equilibrium position of a multi-degree-of-freedom system

is determined by solving a system of algebraic equations, respectively. Here,

by contrast, we ﬁnd that the static-equilibrium position of a beam is deter-

mined by solving a differential equation.

EIw‡

1L 2 k

1L 2

EIw–

1L 2k

w¿

1L 2

EIw‡

10 2k

10 2

EIw–

10 2 k

w¿

10 2

 rAg

w1x,t 2 w

1x 2 w

dyn

1x,t 2

0x0t

x 0

 w

¿10,t 2

Y. Yee, M. Park, and K. Chun, “A sticking model of suspended polysilicon microstructure in-

cluding residual stress gradient and post release temperature,” J. Microelectromechanical Sys-

tems, Vol. 7, No. 3, pp. 339–344 (1998).

On substituting Eq. (9.53) into Eqs. (9.51) and (9.52) and making use

of Eqs. (9.54) and (9.55), we ﬁnd that the oscillations about the static-

equilibrium position are described by

(9.56)

subject to the following boundary conditions at x  0

(9.57a)

and the following boundary conditions at x  L

(9.57b)

Equation (9.56) is a linear, homogeneous partial-differential equation

that is used to describe the free oscillations of the beam about the static-

equilibrium position. As discussed in the context of ﬁnite degree-of-freedom

systems, gravity loading does not appear in the equation governing the

dynamic response w

dyn

(x,t) of the beam. Based on the form of Eq. (9.56), we

assume that there is a separable solution; that is,

(9.58)

where W(x) is a function that depends only on the spatial variable x and G(t)

is a function that depends only on the temporal variable t. By assuming this

form of solution, we are assuming that every point on the beam has the same

time dependence. In other words, the ratio of displacements at two different

points on a beam is independent of time.

On substituting Eq. (9.58) into (9.56) and rearranging the terms, we

obtain

(9.59)

Since the left-hand side consists only of terms that are functions of time and

the right-hand side consists only of terms that are functions of the spatial vari-

able x, the ratio on each side must be a constant; that is,

(9.60)

where l is a constant. Based on the experience gained with free oscillations

of undamped ﬁnite degree-of-freedom systems in Sections 4.2 and 7.4, it

is known that the free oscillations of vibratory systems are described by sine

or cosine harmonic functions.

Noting that the beam is undamped, and



rAW

 l



rAW

dyn

1x,t 2 W1x2G1t 2

EIw‡

dyn

1L,t 2 k

dyn

1L,t 2 M

dyn

1L,t 2

EIw–

dyn

1L,t 2k

w¿

dyn

1L,t 2 J

dyn

1L,t 2

EIw‡

dyn

10,t 2k

dyn

10,t 2

EIw–

dyn

10,t 2 k

w¿

dyn

10,t 2

dyn

 rA

dyn

 0

564 CHAPTER 9 Vibrations of Beams

As discussed in Chapter 4, this will not be true of an unstable vibratory system. In general, for

an undamped linear vibratory system in the absence of rotation, it can be said that unbounded

oscillations do not occur and that the bounded oscillations that do occur are harmonic in form.

assuming that there is no damping in the boundary conditions, we set the con-

stant l as

(9.61)

Upon making use of Eqs. (9.60) and (9.61), we obtain the temporal eigen-

value equation

(9.62)

which has a solution of the form

(9.63)

In the harmonic solution given by Eq. (9.63), G

and G

are arbitrary con-

stants that will be determined by the initial conditions and v is an unknown

quantity to be determined. The quantity v, which describes the frequency of

oscillation of the beam in its free state, is called the natural frequency. As we

will see later in this section, there is an inﬁnite number of natural frequencies

for the beam. On substituting Eq. (9.58) into Eq. (9.56) and making use of

Eq. (9.62), we arrive at

(9.64a)

Since Eq. (9.64a) has to be satisﬁed for all time and for arbitrary G(t) not nec-

essarily zero, the only way this is possible is if we have

(9.64b)

Similarly, substituting Eq. (9.58) into Eq. (9.57) and making use of Eq. (9.62),

we arrive at the following boundary conditions at x  0

(9.65a)

and the following boundary conditions at x  L

(9.65b)

Equations (9.64b) and (9.65) represent the spatial eigenvalue problem. As

in the eigenvalue problems encountered in Chapters 4 and 7, the trivial solution

W(x)  0 is a solution of Eqs. (9.64b) and (9.65). However, we are not interested

in this trivial solution, but in determining the special values of v, called the

eigenvalues, for which W(x) will be nontrivial. In the terminology of spatial

eigenvalue problems, these nontrivial functions are called the eigenfunctions. In

the case of the beam, the eigenvalues provide us the natural frequencies and the

eigenfunctions provide us the mode shapes. The natural frequencies and mode

shapes depend on the boundary conditions and the geometry of the beam. This

dependence will be explored in the following sections.

EIW‡1L 2 k

W1L 2 v

W1L 2 1k

 v

2W1L2

EIW–1L 2k

W¿1L 2 v

W¿1L 2 1k

 v

2W¿1L 2

EIW‡10 2k

W10 2

EIW–10 2 k

W¿10 2

 rAv

W  0

aEI

 rAv

W bG1t2 0

G1t 2 G

sin vt  G

cos vt

 v

G  0

l v

9.3 Free Oscillations 565

9.3.2 Natural Frequencies, Mode Shapes, and

Orthogonality of Modes

We shall now determine the natural frequencies and mode shapes for a gen-

eral set of boundary conditions and discuss an important property of mode

shapes, the orthogonality property. To elaborate on this property and to de-

termine the conditions that go with this property, it is not necessary to deter-

mine explicitly the natural frequencies and mode shapes. Therefore, we ﬁrst

present a discussion on this property, and then we illustrate how Laplace

transforms with respect to the spatial variable can be used to determine the

natural frequencies and mode shapes for uniform beams subjected to arbitrary

boundary conditions.

Orthogonal Functions

An orthogonal function is deﬁned as follows. If a sequence of real functions

(x)}, n  1, 2, . . . , has the property that over some interval

(9.66)

where d

is the Kronecker delta function,

then the functions are said to form

an orthogonal set with respect to the weighting functions p

(x) and p

(x) on that

interval. The quantity is called the norm of the function w

(x). Hence, if m

and n are different from each other—that is, we have two different orthogonal

functions—the integral given by Eq. (9.66) evaluates to zero. This property is

analogous to the orthogonality property associated with vectors; that is, the

scalar dot product of two identical vectors is the square of the vector’s magni-

tude, while the scalar dot product of two orthogonal vectors is zero.

In the present context, the mode shapes W

(x) will take the place of w

(x)

in Eq. (9.66) and the weighting function will be determined by the stiffness

and inertia properties of the system. The material presented here parallels that

presented in Section 7.3.2 for systems with multiple degrees of freedom.

Spatial Eigenvalue Problem in Terms of Nondimensional Quantities

Before proceeding further, we introduce the following notations:

(9.67)m

 rAL, j

 m



, B



j  1,2

 E/r, r

 I/A, t



h  x/L,



 v

rAL



 v



1x 2w

1x 2 p

1x 2

ddx  d

566 CHAPTER 9 Vibrations of Beams

 1, n  m, d

 0, otherwise.

In Eq. (9.67), h is a nondimensional spatial variable,  is a nondimensional

frequency coefﬁcient, c

is the longitudinal (or bar) speed along the x-axis of

the beam, r is the radius of gyration of the beam’s cross-section about the

neutral axis, m

is the mass of the beam, t

is a characteristic time of the beam,

and K

and B

are nondimensional translation and torsion spring constants, re-

spectively. On substituting the appropriate expressions from Eqs. (9.67) into

Eqs. (9.64b) and (9.65), the result is

(9.68)

with the following boundary conditions at h  0

(9.69a)

and the following boundary conditions at h  1

(9.69b)

where the prime () will be used from this point on to denote the derivative

with respect to h. It is noted that in Eqs. (9.68) and (9.69), W(h) has the units

of displacement.

Orthogonality Property of Mode Shapes

We assume that 

is an eigenvalue and W

(h) is the associated eigensolution

or mode shape of the system given by Eqs. (9.68) and (9.69); that is,

(9.70)

and at h  0

(9.71a)

and at h  1

(9.71b)

Let W

(h) be another solution of Eqs. (9.68) and (9.69), which corre-

sponds to the mth natural frequency coefﬁcient 

, where 



. We now

–¿ 11 2 aK





11 2

–112 aB





¿112

‡102K

10 2

–102 B

¿102



 0

W‡11 2 aK





bW11 2

W–11 2 aB





bW¿112

W‡10 2K

W10 2

W–10 2 B

W¿10 2



W  0

9.3 Free Oscillations 567

multiply Eq. (9.70) by W

(h), integrate over the interval 0  h  1, and use

integration by parts to obtain

(9.72)

Performing the same set of operations, but reversing the order of m and n,

we get

(9.73)

After subtracting Eq. (9.73) from Eq. (9.72), the resulting expression is

which is written in expanded form as

(9.74)

Upon substituting the boundary conditions given by Eqs. (9.71) into

Eq. (9.74), we arrive at

(9.75)

Since 



, the expression inside the brackets must equal zero. This

leads to

(9.76a)



dh 

11 2W

11 2

W¿

11 2W¿

11 2 d

1





dh 

11 2W

11 2

W¿

11 2W¿

11 2d 0

 W¿

10 2W –

10 2 0

 W

10 2W‡

10 2 W¿

11 2W–

11 2 W¿

10 2W–

10 2 W¿

11 2W–

11 2

1





dh  W

11 2W –¿

11 2 W

10 2W –¿

10 2 W

11 2W ‡

11 2

1





dh  W

–¿ `

 W

–¿ `

 W

¿W

– `

 W

¿W

– `

 0



–W

–dh 



dh  0



dh 



dh  W

W‡

 W¿

– `



–W

–dh 



dh  0



dh 



dh  W

W‡

 W¿

– `

568 CHAPTER 9 Vibrations of Beams

9.3 Free Oscillations 569

where d

is the Kronecker delta and

(9.76b)

Equation (9.76a) is written as

(9.77)

where d(h  1) is the delta function. Equation (9.77) is a special case of

Eq. (9.66) if we identify x with h, p

(x) with 1  (M

)d(h  1), p

(x) with

)d(h  1), W

(h) with w

(x), and W

(h) with dw

(x)/dx.

Equation (9.76a) represents the orthogonality condition for the beam and

the boundary conditions, and the functions W

(h) that satisfy this condition

are called orthogonal functions. They can be shown to form a complete set of

orthogonal functions.

It is also pointed out that the form of the expression

on the left-hand side of Eq. (9.77) is symmetric in the spatial functions W

(h)

and W

(h); that is, the form of the equation does not change if the functions

(h) and W

(h) are interchanged. This type of symmetry is characteristic

of self-adjoint systems whose eigenfunctions are known to be orthogonal

functions.

Based on Eqs. (9.76) and (9.77), it should be clear that for all of the

boundary conditions shown in Table 9.1, the mode shapes are orthogonal func-

tions. The orthogonality property of the modes was established for beams with

uniform and homogeneous properties; that is, beams with constant ﬂexural

rigidity EI, constant mass density r, and constant area of cross-section A. It can

be shown that an orthogonality condition similar in form to Eqs. (9.76) also ap-

plies to beams with nonuniform and inhomogeneous properties.

Solutions for Natural Frequencies and Mode Shapes

We shall now determine the speciﬁc form of W

(h) by solving Eqs. (9.68) and

(9.69). In order to ﬁnd this speciﬁc form, we ﬁrst need to solve for the eigen-

value 

. To determine this eigenvalue, we need to determine the characteris-

tic equation whose roots will provide us the eigenvalues of the system. The

eigenvalue 

and the associated eigenfunction W

(h) are determined by

solving the boundary-value problem using Laplace transforms. Instead of



W¿

1h 2W¿

1h 2d1h  1 2dh  d



c1 

d1h  1 2dW

1h 2W

1h 2dh





1h 2dh 

11 2

W¿

11 2

E. B. Magrab, ibid, Chapter 1.

L. Meirovitch, Principles and Techniques of Vibrations, Prentice Hall, Upper Saddle River, NJ,

Chapter 7 (1997).