Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

Problems 95

2.47. A designer chooses the dimensions of a component so as to give a safety factor

of 1.5 against fatigue failure based on a reliability of 50%. What will be the probabil-

ity of fatigue failure if the fatigue data for the material follow the Weibull distribution

with modulus b =20?

2.48*. Twelve standard rotating bending tests on nominally identical specimens of a

certain steel yielded the following results for S

′

: 392, 401, 372, 386, 425, 417, 398,

407, 381, 400, 411, 391 MPa. Sketch the cumulative reliability distribution R(S) and

estimate S

and the Weibull parameter b in equation (2.78).

Section 2.3.3

2.49. A bar of rectangular cross section 20 mm ×3 mm has a central hole of diameter

6 mm. Find the maximum tensile stress if the bar is subjected to a tensile force of 5

kN.

2.50. The bar of Problem 2.49 is subjected to a bending moment M =1.8 Nm about

the more ﬂexible bending axis. Find the maximum tensile stress near the hole.

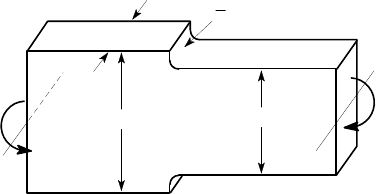
2.51. A bar of thickness 1 in. has a symmetric step change in width from 2 in. to

1.5 in. through a ﬁllet radius of 1/8 in., as shown in Figure P2.51. It is subjected to

a bending moment of 4000 lb in. Find the maximum tensile stress at the change of

section.

4000 lb in

radius

1.5

all dimensions in inches

Figure P2.51

2.52. The bar of Problem 2.49 is subjected to an alternating tensile load F =

cos(

t), where F

= 2 kN. If the bar is machined from AISI 1010 steel (S

= 324

MPa), ﬁnd the safety factor against fatigue failure with a reliability of 50%.

2.53. The bar of Problem 2.51 is machined from AISI 1040 steel for which S

83 ksi. It is subjected to an alternating bending moment M = M

cos(

t). Find the

maximum value of M

if the reliability against fatigue failure is to be no less than

99%. An appropriate value of C

is 0.9.

96 2 Material Behaviour and Failure

2.54. Figure P2.54 shows a cylindrical shaft with a change in section through a ﬁllet

radius of 0.8 mm. The shaft transmits an alternating torque T = T

cos(

t), where

=3 Nm, it is to be manufactured from a steel with S

=800 MPa and is required to

have a reliability of 99.99% against fatigue failure. Determine whether a machined

shaft will meet this requirement, or whether it is necessary to grind the shaft.

0.8 R

φ8

φ10

all dimensions in mm

Figure P2.54

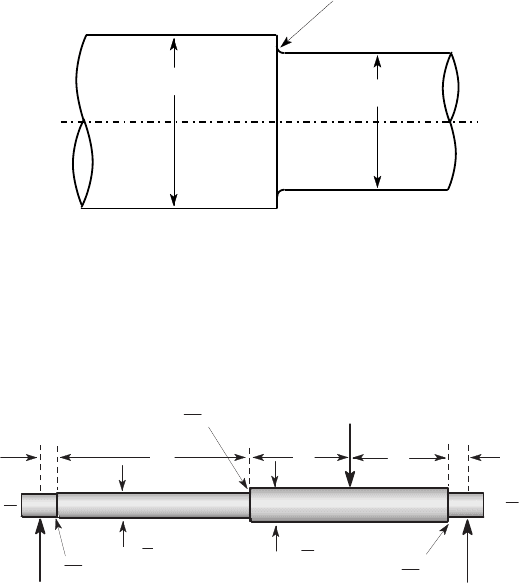
2.55*. The shaft shown in Figure P2.55 is loaded in rotating bending by the 400 lb

force. The shaft is made from steel hardened to 350 BHN and the surface is ground.

Find the factor of safety against fatigue failure, based on a reliability of 50%.

400 lb

all dimensions in inches

Figure P2.55

Hint: After ﬁnding the reactions R

, sketch the bending moment diagram. It

should then be obvious which point will be most likely to fail in fatigue.

Section 2.3.4

2.56. Figure P2.56 shows a bar of cross section 20 ×5 mm with a central hole of di-

ameter 4 mm. It is subjected to a tensile force F which ﬂuctuates between maximum

and minimum values of 10 kN and 8 kN respectively. Determine the safety factor

against eventual fatigue failure with a reliability of 50% if the bar is machined from

steel with S

=324 MPa and S

=210 MPa.

Problems 97

φ 4

all dimensions in mm

Figure P2.56

2.57. A cold drawn rectangular bar is 1.6 in wide, 0.2 in thick and has a machined

central hole of diameter 0.2 in. Estimate the maximum cyclic tensile force (loading

zero to maximum) that can be applied to the bar if the steel has a hardness of 180

BHN and a yield stress of 60 ksi.

2.58. Figure P2.58 shows a spring which is formed from 20 mm ×2 mm cold drawn

steel plate and then hardened to 510 BHN. The bends have an inner radius of 2 mm

for which K

is estimated as 1.9. The force F ﬂuctuates between 40 N and 200 N

during normal service. Estimate the probability of eventual fatigue failure and indi-

cate where it is most likely to occur. Assume a surface factor intermediate between

‘machined’ and ‘hot rolled’ in Figure 2.27.

all dimensions in mm

Figure P2.58

2.59. The fatigue stress concentration factor in an engineering component is esti-

mated to be K

=1.72 and the calculated nominal tensile stresses are

=340 MPa,

= 50 MPa. If the material has an endurance limit S

= 185 MPa, yield stress

=350 MPa and ultimate strength S

=525 MPa, estimate the safety factor against

eventual fatigue failure.

98 2 Material Behaviour and Failure

2.60*. The shaft of the disk sander of Figure P2.60 is made of steel of S

= 900

MPa, S

=750 MPa, S

′

=480 MPa. The most severe loading condition occurs when

pressing the sanding disk against an object near the outer radius with sufﬁcient force

almost to stall the motor. Assuming a coefﬁcient of friction of 0.6 between the disk

and the object and a motor stall torque of 12 Nm, determine the safety factor against

eventual fatigue failure if the relevant surfaces are machined.

radius 1

φ16

φ18

100

fillet

all dimensions in mm

Figure P2.60

2.61. A cylindrical pressure vessel of 1 m diameter is made from hot rolled steel plate

of thickness 4 mm, with properties S

= 800 MPa, S

= 560 MPa, S

′

= 425 MPa. It

is loaded by an internal pressure p, which ﬂuctuates between zero and a maximum

value. Find the maximum permissible working pressure if the vessel is to have an

inﬁnite life with a safety factor of 1.8.

Energy Methods

The ‘intuitive’ or direct way to formulate problems in mechanics of materials is to

analyze the structure into simple components, with internal forces acting between

them. We then use the equations of equilibrium, geometrical conditions and stress-

strain laws to develop a system of governing equations. In some cases, the equilib-

rium equations alone are sufﬁcient to determine the internal forces and the problem

is described as statically determinate. By contrast, in statically indeterminate prob-

lems, the full system of equations must generally be solved, even if only the internal

forces are required.

Energy methods are an alternative to the direct approach — they do not provide

additional information about the system, but instead generally replace one of the

steps in the direct formulation. It is important to know which step is being replaced

by a particular energy formulation, since otherwise we might write what is essentially

the same equation in two different forms and end up with a redundant system of

equations.

The advantages of energy methods will become apparent through the examples

treated in this chapter. Notably, they can often be used to obtain the required answer

without solving for a set of auxiliary quantities that are of no particular interest, and

they also lend themselves to approximate solutions. In particular, they are central to

the development of the ﬁnite element method, which is discussed in more detail in

Appendix A.

Energy methods are a subset of a broader class of methods based on the varia-

tional calculus and known as variational methods. In fact it is possible to develop all

the equations used in this chapter from purely mathematical arguments without ever

making reference to the concept of energy. However, many of the following argu-

ments will be easier for the reader to grasp in an energy formulation, simply because

the physical ideas of conservation of energy and what is involved in doing work on

a system can be called into play to aid our mathematical reasoning.

J.R. Barber, Intermediate Mechanics of Materials, Solid Mechanics and Its Applications 175,

2nd ed., DOI 10.1007/978-94-007-0295-0_3, © Springer Science+Business Media B.V. 2011

100 3 Energy Methods

3.1 Work done on loading and unloading

When a deformable structure is loaded, the applied forces do work. We describe

the structure as elastic if this work can be recovered on unloading, which in turn

requires that the relation between force and deformation is the same on loading and

unloading.

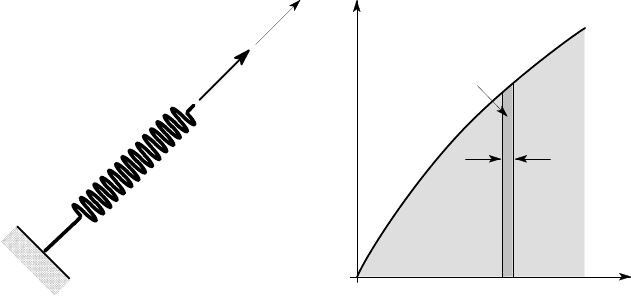
We can illustrate this for the case of the simplest system — a spring subject to

a tensile force F, as shown in Figure 3.1 (a). The displacement u at the end of the

spring increases with F as shown in Figure 3.1 (b).

δu

δW

(a) (b)

Figure 3.1: Work done in extending a spring

The work done during loading W is given by the product of the force and the dis-

tance through which it acts. However, the force F varies during the process because

F is a function of u, so we have to develop an expression for W in integral form. We

ﬁrst note that the increment of work done

W in increasing the displacement from

u to u+

u is F(u)

u (the product of the instantaneous force and the increment of

displacement). This increment of work done is equal to the area of the darkly shaded

strip in Figure 3.1 (b). The total work done W can be seen as the sum of a set of

similar strips and is therefore equal to the area under the force-displacement curve,

shown with lighter shading in Figure 3.1 (b). It is obtained by integration as

W =

F(u)du . (3.1)

If the structure is elastic, the same relation will hold between F and u during both

loading and unloading and the work done by the force on loading will be exactly

equal to that done against the force (and hence recovered) during unloading. For

inelastic structures, the unloading curve lies below the loading curve, as in Figure

3.2, and not all the work will be recovered. There will be a loss corresponding to the

shaded area between the two curves. This is called hysteresis loss and the lost work

is generally released in the form of heat.

3.2 Strain energy 101

unloading

Figure 3.2: Hysteresis losses on loading and unloading

An important class of elastic structures is that for which the load-displacement

relation is linear as shown in Figure 3.3. In this case, we can deﬁne a stiffness k such

that

F = ku . (3.2)

In other words, k is the slope of the straight line in Figure 3.3. It follows from equa-

tions (3.1,3.2) that the work done in extending a linear spring of stiffness k is

W =

kudu =

. (3.3)

Figure 3.3: Linear load-displacement relation

3.2 Strain energy

Since the work we do on loading an elastic structure is recovered on unloading,

it is natural to think of the energy as being ‘stored’ in the deformed structure. In

102 3 Energy Methods

other words, we think of the structure as a kind of reservoir for energy that is ﬁlled

up during loading and emptied during unloading. The energy stored in this way is

referred to as strain energy and is denoted by the symbol U. Since there is no energy

loss,

U = W . (3.4)

In other words, the strain energy stored in the structure in a deformed state is equal

to the total net work we had to do on the structure to deform it.

The easiest way to ﬁnd U is to devise a simple loading history or scenario that

will lead to the desired state and then sum the work we have to do to get there. For

the simple case of a linear spring, equations (3.3, 3.4) lead to the expression

U =

. (3.5)

Two alternative forms of this equation can be obtained using equation (3.2). We have

U =

Fu (3.6)

and

U =

. (3.7)

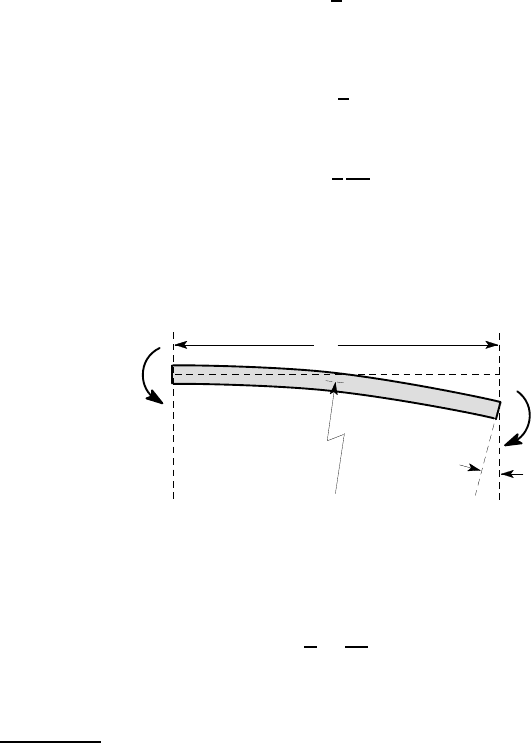
Example 3. 1

A uniform elastic beam of length L, and ﬂexural rigidity EI, is subjected to equal and

opposite moments M at each end. Find the strain energy stored in the beam.

Figure 3.4: Initially straight beam in bending

If the beam is initially straight, it will bend into a circlular arc, as shown in Figure

3.4. The radius of curvature R is given by the classical bending equation (1.17) as

(3.8)

and hence, if the left end of the beam is ﬁxed,

the right end will rotate through an

angle

It is not necessary to impose this restriction. If both ends of the beam rotate, both moments

will do work, but the net work done depends only on the difference between the rotations of

3.3 Load-displacement relations 103

. (3.9)

The moment at the right end of the beam therefore does work during its application,

leading to the result

U = W =

, (3.10)

where we have used equation (3.9) to express M in terms of

By analogy with equations (3.6,3.7), we can use (3.9) to obtain the alternative

expressions

U =

(3.11)

and

U =

2EI

(3.12)

for the strain energy stored in a beam subject to pure bending.

Notice that the work done by a moment is the product of the moment and the

angle (in radians) through which it acts. All the energy arguments in this chapter

can be restated to apply to moments or torques by replacing forces by moments and

displacements by rotations.

3.3 Load-displacement relations

We have suggested that an elastic component can be considered as a kind of reservoir

for strain energy. It follows that, for a structure made up of several connected com-

ponents, the strain energy stored is simply the sum of that stored separately in each

of the components. This can be proved formally by drawing free-body diagrams for

the separate components and noting that the work done by the internal forces thereby

exposed must sum to zero, because internal forces will appear in equal and opposite

pairs that move through the same displacements.

This result can be used to obtain a very efﬁcient solution for the local displace-

ment of a determinate elastic structure due to a single external force F. We ﬁrst draw

free-body diagrams for the various components of the structure, use the arguments

of the previous section to ﬁnd the strain energy stored in each component and add

up the various contributions. We then equate this expression to the work done in

applying the force, given by equation (3.1).

the two ends, which is still given by (3.9). Another way of stating this is to decompose the

motion into (i) that in which the left end is ﬁxed and (ii) an arbitrary rigid body rotation.

During the rigid body rotation, the two end moments do equal and opposite amounts of

work that are therefore self-cancelling. In fact, a more general theorem of this kind can be

proved — viz. that a self-equilibrated system of forces acting on a body does no work if the

body executes an arbitrary rigid mody motion.

104 3 Energy Methods

If the structure is linear — i.e. if all the components obey Hooke’s law and the

deformations are small — we can then use (3.6) to write

U =

Fu ; u =

(3.13)

to get an immediate expression for the displacement u.

However, the method can also be used for non-linear problems. If we write u(F)

as the displacement due to the force F, the work done W and hence the strain energy

U can be written in terms of u(F) as

U = W =

dF . (3.14)

Differentiating with respect to F, we then have

∂

. (3.15)

Thus, if the strain energy is a known (non-linear) function of F, we can determine

du/dF and hence integrate it to obtain u(F). In the special case of linearity, U will

be quadratic in F [see for example equation (3.7)], the right hand side of (3.15) will

be constant and the result reduces to (3.13).

Example 3. 2

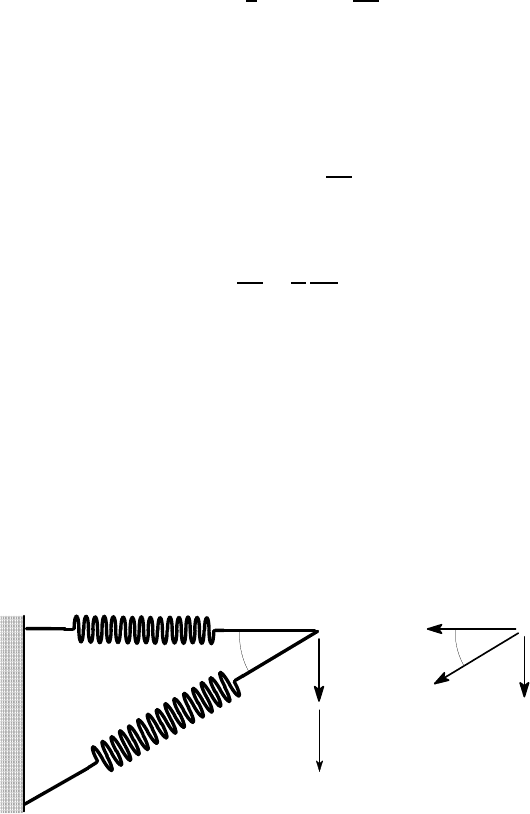
Find the vertical displacement u of the point A for the structure of Figure 3.5(a),

loaded by a vertical force, F. The linear springs are assumed to be capable of trans-

mitting loads in either tension or compression, without buckling.

(a) (b)

Figure 3.5: A structure loaded by a single external force F

First, we use the equilibrium equations to ﬁnd the tensile forces F

in the two

springs of stiffness k

respectively. Equilibrium of the pin at A (Figure 3.5 (b))

demands that