Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

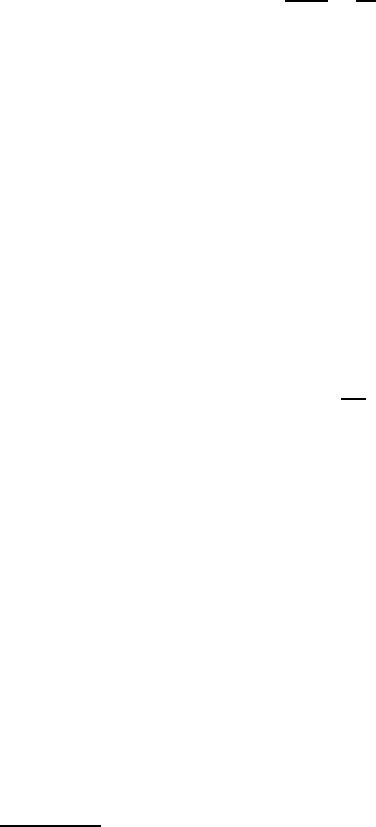
3.5 The principle of stationary potential energy 115

Notice that the constant

Ω

representing the potential energy in the horizontal

position, disappears on differentiation. The value of

Ω

is therefore of no importance

to the calculation and the datum for potential energy can be chosen arbitrarily.

We can also determine the stability of the deformed conﬁguration by performing

a second differentation. We obtain

∂

Since springs must have positive stiffnesses, this derivative is positive and it follows

that equation (3.40) deﬁnes a minimum of total potential energy and hence a stable

equilibrium conﬁguration. We shall return to the question of stability of elastic sys-

tems in Chapter 12. The remainder of this chapter will be limited to the use of energy

methods in the determination of equilibrium conﬁgurations.

3.5.1 Potential energy due to an external force

Example 3.4 was formulated in terms of gravity, since the concept of gravitational

potential energy will be familiar to many readers from elementary physics and dy-

namics. However, the problem would be essentially unchanged if the bar, instead of

having mass M, were subjected to a vertical external force F of magnitude Mg at its

mid-point B. The displacement could then be written in terms of F as

We can generalize the idea of the potential energy to describe the effect of an

external force F in any direction. The potential energy of such a force is

Ω

= −F · u , (3.41)

where u is the displacement of its point of application from some ﬁxed datum. Thus,

Ω

is the work done against the force during the deformation. The force is assumed to

be constant

and apply throughout the motion, so if the deformation were reversed,

this work would be recovered and is therefore legitimately deﬁned as potential en-

ergy.

3.5.2 Problems with several degrees of freedom

In Example 3.4, the bar has only one degree of freedom. Once u

is speciﬁed, the

position of the bar and hence the extensions of the two springs are deﬁned. The

position of the bar could alternatively have been characterized using the angle

See footnote 5 on page 110.

Notice once again that there is no factor of 1/2 in this expression, since the force remains

constant throughout the deformation, in contrast to that in a spring which increases linearly

from zero during extension.

116 3 Energy Methods

from the horizontal (see Figure 3.10 (b)). We would then have to determine the strain

energy and potential energy in terms of

instead of u

and the statement of the

principle of stationary potential energy would be written

∂Π

∂θ

=0. The same ﬁnal

result would be obtained.

A good strategy is to sketch the system in a representative deformed conﬁgu-

ration and then determine the minimum number N of independent displacements

and/or angles needed to deﬁne the conﬁguration completely. We shall refer to these

displacements and/or angles as the degrees of freedom of the system and refer to

them as u

, where i = (1,N). In view of the above discussion, it is clear that the

choice of the u

is not unique, but the number of degrees of freedom N must be the

same whatever choice is made.

The degrees of freedom u

completely deﬁne the deformed conﬁguration and

hence they also deﬁne the extended length of all springs and the distance moved by

all external forces. We can therefore write the strain energy and potential energy in

terms of the u

. The principle of stationary potential energy is then written in the

form that the partial derivative of

with respect to each degree of freedom must be

zero — i.e.

∂Π

∂

= 0 (3.42)

for i=(1,N). This provides N equations to determine the N unknowns u

, and hence

determine the deformed conﬁguration of the system.

Example 3. 5

Determine the horizontal displacement of the point A for the structure of Figure

3.5(a), loaded by a vertical force F.

This system has two degrees of freedom, since (i) we need two coordinates to

deﬁne the position of the point A and (ii) the springs are extensible so there are no

kinematic constraints on this position within the plane. The choice of degrees of

freedom is arbitrary, but a convenient choice is to take the horizontal and vertical

displacements of A as u

respectively, as shown in Figure 3.11.

Figure 3.11: Displacements of the point A

With these displacements, the potential energy of the force F is

Ω

= −Fu

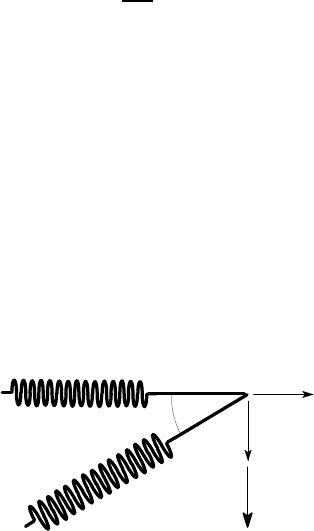
3.5 The principle of stationary potential energy 117

To ﬁnd the strain energy stored in the two springs in terms of the two degrees

of freedom u

, we need to use kinematic arguments to ﬁnd the extensions of the

springs.

If the displacements u

are small in comparison with the original lengths of

the springs, the change in length of each spring depends only on that component

of displacement parallel to the spring. For example, the horizontal displacement u

causes an increase in length

= u

in spring 1, but the vertical displacement u

causes no increase in length. Instead, it simply causes spring 1 to rotate about its

ﬁxed support through a small clockwise angle, as shown in Figure 3.12 (a).

(a) (b)

Figure 3.12: Kinematics of spring extension

Similarly, the extension

of spring 2 depends only on the component of dis-

placement parallel to spring 2. We can ﬁnd this by resolving the components u

into this direction, as shown in Figure 3.12 (b), with the result

= u

cos30

−u

sin30

We can now write the strain energy in the two springs as

√

−

Collecting results, we have

Ω

= −Fu

−

√

The principle of stationary potential energy now gives the two equations

∂Π

∂

= 0 ;

∂Π

∂

= 0 ,

from which

−

√

= 0 (3.43)

−

√

−F = 0 . (3.44)

118 3 Energy Methods

The solution of these equations is





F ; u

√

. (3.45)

Notice that the vertical displacement u

is the same as we obtained in §3.3 [equa-

tion (3.21)], as we should expect, but the earlier method (equating the work done by

the force to the total strain energy stored) was unable to give a value for the horizontal

displacement u

Notice also that the same equations (3.43, 3.44) could have been obtained by

ﬁnding the forces in the springs from their extensions and then writing two equilib-

rium equations for the pin at A. The forces in the springs are given by

= k

cos30

−u

sin30

) .

Substituting these results into the equilibrium relations (3.16, 3.17) for the pin at A,

we obtain (3.43, 3.44) as before.

3.5.3 Non-linear problems

In developing the principle of stationary potential energy, we appealed to the idea that

a system cannot escape from a minimum energy state unless some external energy

source is provided. This argument makes no assumptions about linearity and hence

the principle can be applied to non-linear systems, provided the components are all

elastic.

Non-linear effects can arise in mechanics problems from two sources. Material

non-linearities occur if the components are constructed from non-linear elastic ma-

terials — i.e. materials for which stress and strain are not linearly related, but which

do follow the same curve on loading and unloading. Geometric non-linearities arise

when the displacements are no longer small in comparison with the dimensions of

the structure. In both cases, the principle of superposition fails — i.e. when two loads

are applied to a structure, the deformation is not generally equal to the sum of that

produced by each load acting separately.

The application of the principle of stationary potential energy involves the same

steps as in linear problems, but of course the non-linearity of the resulting equations

generally leads to more complicated algebra.

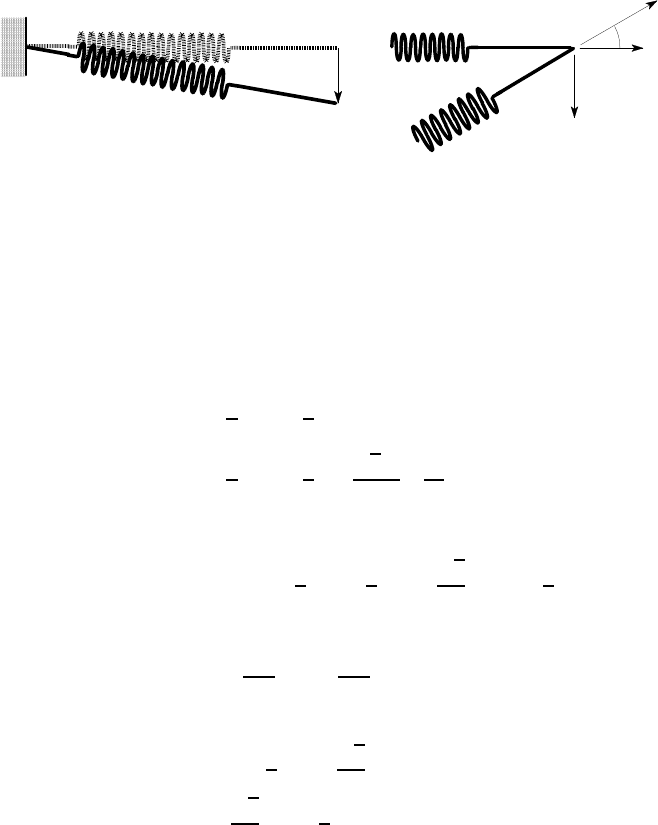
Example 3. 6

Figure 3.13 (a) shows a mass M which is free to slide in a frictionless vertical groove

and attached to a spring. The spring is unstretched in the horizontal conﬁguration

This condition is important since for inelastic components, some of the work done during

loading is dissipated as heat and is not recoverable on unloading.

3.5 The principle of stationary potential energy 119

of Figure 3.13 (a) and has a non-linear relation between tensile force F and the

extension u given by

F = Cu

as shown in Figure 3.14. Find the equilibrium conﬁguration of the system.

(a) (b)

Figure 3.13: Mass constrained by a groove and supported by a non-linear spring

F = Cu

Figure 3.14: Force extension curve for the non-linear spring

As in equation (3.1), we can compute the strain energy stored in the spring by

equating it to the work done during extension, with the result

U =

du =

. (3.46)

The mass has one degree of freedom which we shall characterize by the angle

between the spring and the horizontal in the deformed position, as shown in Fig-

ure 3.13 (b). We shall make no assumptions about smallness of the deformations

and hence the problem exhibits both material and geometric non-linearity. In the

deformed position, the potential energy of the mass is

Ω

= −MgL tan

and the deformed length of the spring is Lsec

, corresponding to an extension

u = L(sec

−1) .

Substituting into equation (3.46), we obtain

120 3 Energy Methods

U =

(sec

−1)

and hence

= U +

Ω

(sec

−1)

−MgL tan

The equilibrium conﬁguration is then determined from the condition

∂Π

∂θ

(sec

−1)

sin

cos

−

MgL

cos

= 0

and hence

sin

(sec

−1)

which can be solved numerically for

3.6 The Rayleigh-Ritz method

To use the principle of stationary potential energy, we have to characterize the kine-

matics of the deformation in terms of a ﬁnite number of degrees of freedom u

and

this can only be done for systems consisting of rigid bodies connected by springs. By

contrast, a continuous elastic body (e.g. a laterally-loaded beam) has an inﬁnite num-

ber of degrees of freedom, because it is capable of being deformed into an inﬁnity of

different shapes by appropriate external loads.

However, we can use the principle of stationary potential energy to develop an

approximate solution to the problem. We ﬁrst assume some approximate form for

the solution, containing a number of arbitrary constants, which constitute the degrees

of freedom in the solution. We then use the stationary potential energy theorem to

determine ‘optimal’ values for these constants. This is known as the Rayleigh-Ritz

method. It is similar to the process of ﬁtting the best curve to a set of data points,

where ‘best’ is here interpreted in the sense of minimizing some measure of error,

such as the sum of the squares of the shortest distances from the points to the line (the

so-called ‘least squares’ ﬁt). The principle of stationary potential energy provides a

natural criterion for choosing the best approximation in a given class.

By approximating the deformation by an expression with a ﬁnite number of de-

grees of freedom, we are constraining the solution to lie in a subset of the actually

inﬁnite number of kinematically possible states of deformation. The accuracy of the

resulting approximation will clearly depend on the choice of this subset. There are

no deterministic rules for choosing an appropriate approximate form, other than the

requirement that it should satisfy the kinematic boundary conditions of the problem.

The best strategy is to rely on our ‘non-engineering’ intuition (see Chapter 1) to

sketch the expected deformed shape of the body and only then seek a mathematical

expression that can describe this shape. We shall give various examples of this pro-

cess and its effect on the accuracy of the resulting approximation in the following

pages.

3.6 The Rayleigh-Ritz method 121

Example 3. 7

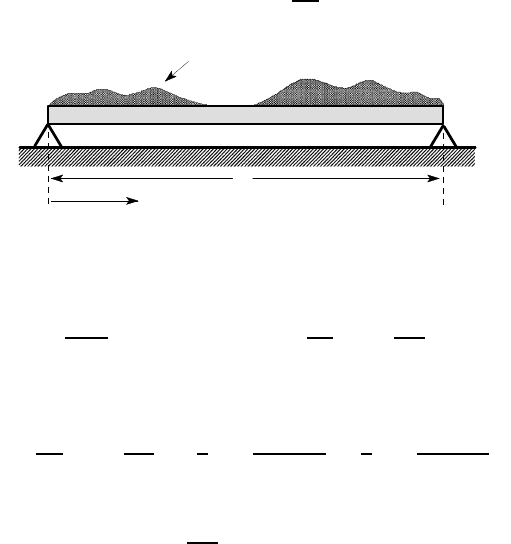
A cantilever beam is built-in at z = 0 and subjected to a uniformly distributed load

per unit length, as shown in Figure 3.15. Use the Rayleigh-Ritz method to ﬁnd an

approximate expression for the deﬂection of the beam.

Figure 3.15: Cantilever subjected to a uniform lateral load

Clearly, the beam will bend downwards, but for consistency with other beam

problems in Chapters 4,7,12, we shall use the sign convention that positive dis-

placements u(z) are upwards. The slope and deﬂection must be zero at z = 0 —

i.e. u(0) = u

′

(0) = 0 — so we assume the simplest polynomial approximation that

satisﬁes these conditions, which is

u = Cz

. (3.47)

This is a one term approximation — i.e. there is only one degree of freedom, rep-

resented by the constant C which must be determined by applying the principle of

stationary potential energy.

In order to determine the strain energy, we need to express equation (3.24) in

terms of the displacement, rather than the bending moment. Noting that

M = −EI

from the elementary bending theory, and substituting for M into (3.24), we obtain

U =





dz . (3.48)

Substituting for u from equation (3.47) and evaluating the integral, we ﬁnd

U =

(2C)

dz = 2EIC

L .

The potential energy of the external load

Ω

can be found by thinking of the load

as a set of concentrated forces, w

dz, each of which moves downwards through a

distance (−u), since the sign convention for u is positive upwards. Thus,

Ω

u(z)dz = w

dz =

The total potential energy is therefore

w per unit length

122 3 Energy Methods

= U +

Ω

= 2EIC

L +

and the principle of stationary potential energy

∂Π

∂

C =0 then gives

4EICL +

= 0 and hence C = −

12EI

Substituting this result into equation (3.47), we obtain the approximate solution for

the displacement of the beam as

u(z) = −

12EI

. (3.49)

Of course, this problem can very easily be solved exactly by using equilibrium

arguments to ﬁnd the bending moment and then integrating the bending moment-

curvature relation. The exact expression for the displacement is

u = −



−



. (3.50)

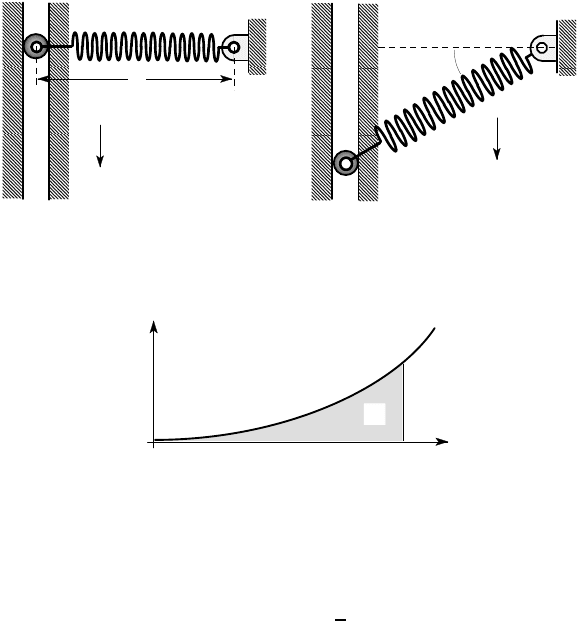
Figure 3.16: Comparison of exact and approximate solutions for u(z)

The exact and approximate deﬂection curves are compared in Figure 3.16. The ap-

proximate expression signiﬁcantly underestimates the actual deﬂection. For example,

it predicts only two thirds of the correct displacement at the free end B. The approx-

imation is even poorer in other more detailed respects. For example, it is based on a

constant curvature along the beam and hence implies a constant bending moment

M = −EI

whereas the actual bending moment is a function of z given by

M =

(L −z)

Thus, the approximation underestimates the maximum bending moment (at z = 0) by

a factor of 3.

3.6 The Rayleigh-Ritz method 123

These results are fairly typical for a Rayleigh-Ritz approximation with only one

degree of freedom. The approximation will generally be found to underestimate max-

imum deﬂections by anything up to 50% and signiﬁcantly larger errors will be found

in estimates for force resultants or stresses. The underestimate is associated with the

fact that the assumed approximate form constrains the permitted shape of the body

and hence tends to produce a stiffening effect. The true equilibrium state must have a

lower total potential energy than the approximate one and this implies that if the con-

straint is relaxed, the external loads will lose potential energy by moving in their own

directions. This trend will also be apparent if the constraint is partially removed by

the addition of one or more additional degrees of freedom. Thus, the addition of an

extra degree of freedom always moves the total energy nearer to the true equilibrium

state and hence is associated with an improvement in accuracy.

There are ways to improve the accuracy of the Rayleigh-Ritz approximation

without making the calculation signiﬁcantly more complicated, but we should not

underestimate the value of a method that can produce an estimate even within 50%

of the correct result using such a simple procedure. In this context, we note

(i) In the early stages of the design process, we often want just an order of magni-

tude estimate of a physical quantity, to determine which components, quantities

or locations are critical in the proposed design and hence whether the concept

is feasible (see Chapter 1). When these strategic questions have been answered,

there are many techniques available (all of course much more time consuming)

for getting more accurate predictions for the limited number of quantities that

have been identiﬁed as critical.

(ii) Although the numerical values obtained from the method are grossly approx-

imate, the parametric form is correct. For example, equation (3.49) correctly

predicts that the maximum deﬂection will be a numerical multiple of wL

/EI.

This is very useful in the design process, since it gives us a good indication of

what changes in the design parameters will be beneﬁcial and how much effect

they will have. By contrast, similar information can be obtained from purely nu-

merical methods only by performing multiple solutions for different parameter

values and analyzing the results.

(iii) In Example 3.7, the exact solution is not much more difﬁcult than the approx-

imate one and we have deliberately made this choice to enable simple compar-

isons to be made. To get a more realistic idea of the relative simplicity of the

method, the reader should consider a more complex problem such as Problem

3.20. The exact solution for this indeterminate problem would involve the use of

singularity functions and the imposition of boundary conditions would then lead

to a set of simultaneous algebraic equations. By contrast, the Rayleigh-Ritz so-

lution would be only marginally more complicated than Example 3.7. In fact, the

reader is recommended to think through the procedure involved in a conventional

solution to any of the problems he/she solves using any of the energy methods

This is one of the major advantages of the use of total potential energy as a criterion for

the ‘best’ approximation. It ensures that the addition of extra degrees of freedom always

improves the approximation, regardless of the choice of form.

124 3 Energy Methods

treated in this chapter, in order to develop a sense of the relative advantages of

the various methods in different contexts.

3.6.1 Improving the accuracy

The obvious way to improve the accuracy of a Rayleigh-Ritz approximation is to

use a representation with more degrees of freedom. From an algebraic point of view,

there are practical limits to this process. We saw in Example 3.5 that even the use

of two degrees of freedom signiﬁcantly increases the complexity of the solution and

it largely defeats the object of the excercise to use more than two. The only excep-

tions to this rule are those in which the terms corresponding to additional degrees of

freedom can be described in a suitably condensed notation, such as a series.

Series solutions

Consider, for example, the simply-supported beam of Figure 3.17, subjected to a dis-

tributed load w(z). A fairly general approximation to the deformed shape, satisfying

the end conditions u(0)=u(L)= 0 can be written in terms of the Fourier series

u(z) =

∑

i=1

sin





. (3.51)

Figure 3.17: Simply-supported beam subjected to arbitrary loading w(z)

The strain energy is then found by substituting (3.51) into (3.48), with the result

U =

∑

i=1

∑

j=1

sin





sin





dz . (3.52)

To evaluate the integral, we use the results

sin





sin





cos



(i − j)



−

cos



(i + j)



cos





dz = 0 ; n 6= 0

= L ; n = 0 , (3.53)

w(z) per unit length