Барковський В.В., Барковська Н.В. Вища математика для економістів

Подождите немного. Документ загружается.

321

Частина 11. Визначені та невласні інтеграли

Частина 11

ВИЗНАЧЕНІ ТА НЕВЛАСНІ ІНТЕГРАЛИ

Визначений інтеграл є одним із основних понять математичного

аналізу

і широко використовується в різних галузях науки, техніки

та

в економічних дослідженнях.

11.1. Означення та властивості визначеного інтеграла

11.1.1. Задачі, що привели до поняття визначеного інтеграла

Розглянемо

дві задачі – геометричну та фізичну.

1. Обчислення площі криволінійної трапеції. Нехай на відрізку





визначена неперервна функція



fx

і будемо поки що

вважати

, що



0fx

для усіх







Фігуру, обмежену кривою



fx

, відрізком





осі

, пря!

мими

a

та



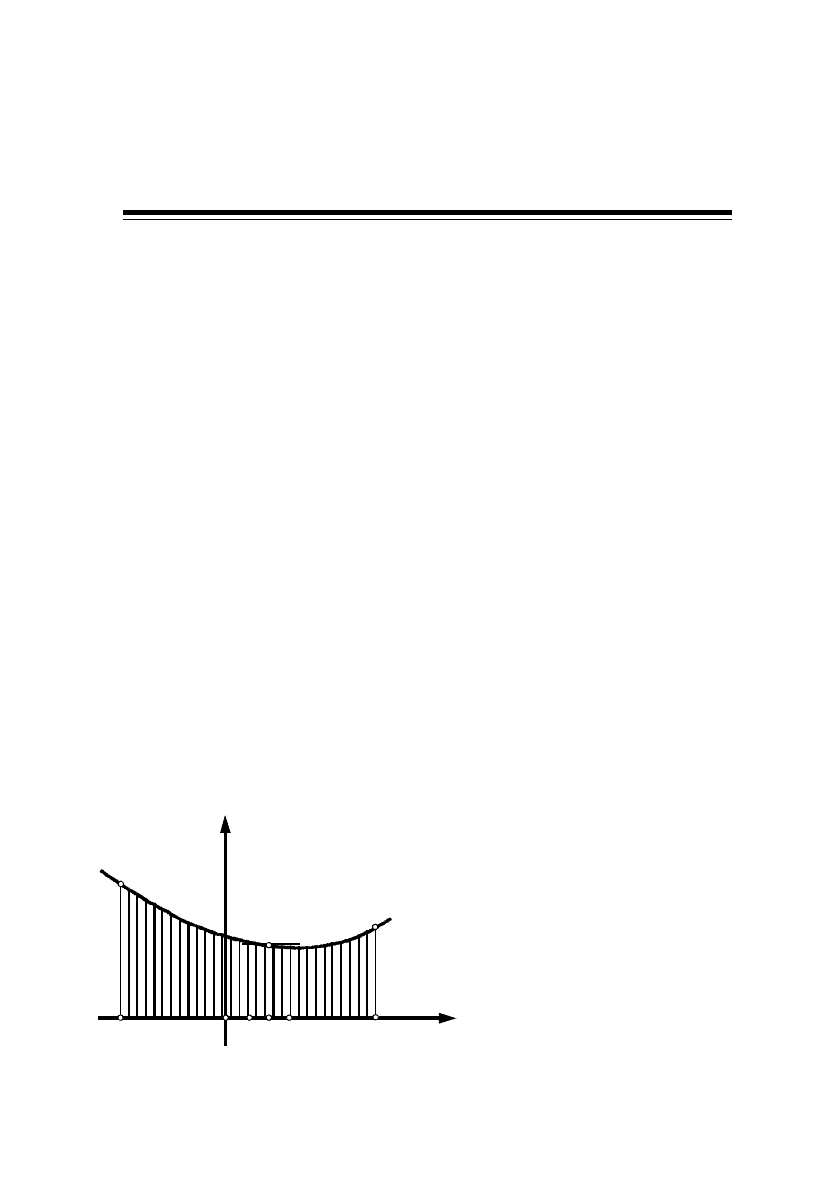
, називають криволінійною трапецією (див.

мал. 1). В окремих випадках може



fa

або



fb

і тоді

відповідна

сторона трапеції стягується в точку.

Для обчислення площі

цієї криволінійної трапеції

поділимо

відрізок





,ab

до!

вільним чином на

частин

точками

012 k

ax x x x

b 

Довжини цих частин

,1,2,,

kkk

xxx k n



  



y = f(x)

k–1

N–1



Мал. 1.

322

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

Перпендикуляри до осі

, проведені із точок ділення до пере!

тину із кривою





, розділяють усю площу трапеції на

вузь!

ких криволінійних трапецій. Замінимо кожну із цих трапецій пря!

мокутником з основою



та висотою





, де

kkk







Площа кожного такого прямокутника дорівнює







Сума площ усіх таких прямокутників буде дорівнювати

   

11 2 2

nn kk

fxfx fx fx

  



     



 .

Таким чином, площа

криволінійної трапеції наближено дорів!

нює цій сумі, тобто



Sf x









Ця формула буде тим точнішою, чим менша величина



Щоб одержати точну формулу для обчислення площі

криво!

лінійної трапеції, треба в цій формулі перейти до границі, коли

x

Тоді



max 0

lim

Sfx











. (1)

2. Обчислення шляху, який пройшла точка. Нехай по!

трібно визначити шлях

, який пройшла матеріальна точка, що

рухається

в одному напрямі із змінною швидкістю



за час

від

до

Поділимо проміжок часу

Tt

на

частин:

,,,.

tt t 



Позначимо через



довільний момент часу із проміжку

t

а зна!

чення швидкості у цій точці позначимо



,1,2,,.

Vf k n







323

Частина 11. Визначені та невласні інтеграли

11.1.2. Означення визначеного інтеграла та його зміст

Нехай

функція



задана на відрізку





. Розіб’ємо цей

відрізок

на

частин точками ділення

012

ax x x x b

У кожному проміжку











довжиною

kkk



 

обере!

мо довільну точку



і обчислимо відповідне значення функції





1,2,...,

kn

Побудуємо суму











, яку називають інтегральною су!

мою для функції



на відрізку





Точка, що рухається з постійною швидкістю

на проміжку часу

t

, проходить за цей час шлях

Vt

, а за час

Tt

вона пройде шлях



11 2 2

nn kk k k

Vt Vt Vt Vt f t





       





Будемо вважати, що шлях

, пройдений точкою, наближено до!

рівнює цій сумі. Коли

t

, тоді змінна швидкість на проміжку

t

мало відрізняється від постійної

. Тому дійсне значення шля!

ху, пройденого точкою за час

Tt

буде дорівнювати границі цієї

суми

при

max 0

t

, тобто



max 0

lim

Sft











. (2)

До аналогічної суми зводиться задача про роботу змінної сили,

що направлена по прямій лінії – траєкторії руху точки, до якої при!

кладена ця сила та інші задачі.

324

Барковський В.В., Барковська Н.В. «Вища математика для економістів»



Означення 1. Якщо існує скінчена границя інтегральної суми

при

max 0

x

, незалежна від способу ділення відрізка





на ча&

стини та вибору точок



, то ця границя називається визначеним

інтегралом від функції



на відрізку





і позначається



fxdx



Математично це означення можна записати так:

  

max 0

lim

fxdx f x













. (3)

Відмітимо, що числа

та

називають нижньою та верхньою

межами

, відповідно.

Згідно з цим означенням рівності (1) та (2) тепер можна записа!

ти у вигляді

 

SfxdxSftdt



(4)

тобто площа криволінійної трапеції

та шлях

, пройдений точкою

із

змінною швидкістю



Vft

виражаються визначеним інтегралом.

Перевірка існування скінченої границі інтегральної суми для

кожної

функції утруднена. Але такої перевірки робити не треба тому,

що використовують таку відому теорему.



Теорема 1. Якщо функція



неперервна на відрізку





або обмежена і має скінчену кількість точок розриву на цьому

відрізку, то границя інтегральної суми існує, тобто функція



інтегрована на





325

Частина 11. Визначені та невласні інтеграли

11.1.3. Основні властивості визначеного інтеграла

Із

означення (3) визначеного інтеграла та основних теорем про

границі

випливають слідуючі властивості.

Постійний множник можна виносити за знак визначеного інтег!

рала, тобто якщо

– стала, то

 

fxdx A fxdx



Визначений інтеграл від алгебраїчної суми скінченої кількості

функцій

дорівнює такій самій алгебраїчній сумі інтегралів від кож!

ного доданку, тобто

  

bb b

aa a

fx fx f x dx

f x dx f x dx f x dx



 







 



3. Якщо поміняти місцями межі інтегрування, то визначений

інтеграл

змінює свій знак на протилежний, тобто

 

xdx f xdx



Визначений інтеграл з рівними межами дорівнює нулю, тобто



fxdx



для будь!якої функції



Якщо

 

fx x











то



()

fxdx xdx







Якщо

та

– найбільше та найменше значення функції



на відрізку





, то

326

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

11.2. Обчислення визначених інтегралів

Раніше ми навчились знаходити невизначені інтеграли. Тому для

обчислення

визначених інтегралів доцільно встановити зв’язок між ними.

11.2.1. Зв’язок між визначеним та невизначеним інтегралами



Означення 2. Визначений інтеграл з постійною нижньою ме&

жею та змінною верхньою межею називають інтегралом із змінною

верхньою межею

Щоб мати звичне позначення, змінну верхню межу позначимо

через

, а змінну інтегрування

. Одержимо інтеграл



tdt



, який

є функцію

, тобто

 

Ф xftdt





Теорема 2. Якщо



неперервна функція, то похідна

визначеного інтеграла від неперервної функції по змінній верхній

межі дорівнює значенню підінтегральної функції для цієї верх

ньої межі, тобто

  

xftdtfx















. (5)

  

mb a f xdx Mb a  



  

fxdx f b a







, де





  

bcb

aac

xdx fxdx f xdx



;

acb



327

Частина 11. Визначені та невласні інтеграли

Доведення. Надамо аргументу

приріст

x

, тоді функція



Ф x

одержить приріст, який згідно з властивістю 8 визначеного інтеграла

можна

записати у вигляді

   

   

xxxx xx

axa x

Фx Фx x Фx

f t dt f t dt f t dt f t dt

 



 



До останнього інтеграла застосуємо властивість 7, тоді

   

Ф x

xxx



 

, де





Згідно з означенням похідної маємо



 

00 0

lim lim lim

xx x

xfx

xffx



  





 



що й треба було довести.



Теорема 3. Визначений інтеграл від неперервної функції до

рівнює різниці значень будьякої її первісної для верхньої та ниж

ньої меж інтегрування, тобто якщо



є первісна функції



, то має місце рівність

  

fxdx Fb Fa



, (6)

яка називається формулою НьютонаЛейбніца.

Доведення

. Нехай



деяка первісна функції



fx. За теоре!

мою 2



tdt



також первісна для



. Але дві первісні функції



відрізняються лише на постійний доданок

. Тому

  

ftdt Fx C



. (7)

328

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

Ця рівність (7) при відповідному обранні

буде тотожністю,

тобто має місце для усіх

Для визначення

візьмемо у формулі (7)

a

. Тоді

   

ftdt Fa C Fa C C Fa  



Отже,

    

tdt Fx Fa



Якщо у цій рівності покласти



, то одержимо

    

ftdt Fb Fa



Змінюючи змінну інтегрування

на

, одержимо формулу (6),

що й треба було довести.

Відмітимо, що різницю

 

bFa



позначають часто так:



, тобто

  

xFbFa



Тому формулу Ньютона!Лейбніца (6) можна записати у вигляді

 

xdx Fx





Ця формула вказує не тільки на зв’язок визначеного інтеграла з

невизначеним

, але й спосіб обчислення



fxdx





Приклад 1. Обчислити

3xdx





329

Частина 11. Визначені та невласні інтеграли



Розв’язання.



22 33

33 3 21819

113

xdx xdx x









11.2.2. Інтегрування частинами

Якщо

проінтегрувати обидві частини рівності

     

dux vx vxdux uxdvx



 



в межах від

до

, то одержимо

    

bbb bb

aaa aa

duxvx vxdux uxdvx uv vdu udv



  



 

Звідси одержуємо важливу формулу інтегрування частинами виз!

наченого інтеграла:

udv u v vdu

 



. (8)



Приклад 2. Обчислити інтеграл

cosxxdx







Розв’язання. Нехай

ux

cosdv xdx

, тоді знаходимо

du dx



cos sinvxdxx



(взята первісна без сталої С).

Застосовуючи до заданого інтеграла формулу (8), одержимо

cos sin sinxxdxxx xdx





 



2sin2 0sin0cos cos2 cos00x



 

     

330

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

11.2.3. Заміна змінної у визначеному інтегралі



Теорема 4. Нехай задано інтеграл



xdx



, де



не

перервна на відрізку





,ab . Зробимо підстановку











, де





неперервна диференційована функція на

відрізку







Якщо:

1) при зміні

від



до



змінна

змінюється від

до

, тобто

 

 



;

2) складна функція













визначена і неперервна

на відрізку







, тоді має місце рівність

   

fxdx f t tdt















. (9)

Доведення. Нехай



деяка первісна для функції



, тобто

 





. Розглянемо складну функцію













. Застосовую!

чи правило диференціювання складної функції, одержимо



   

dF t

ttftt



 





 

 



 

Це означає, що функція













є первісною для функції

 









Звідси, за формулою Ньютона!Лейбніца і рівностей







та







, одержуємо