Барковський В.В., Барковська Н.В. Вища математика для економістів

Подождите немного. Документ загружается.

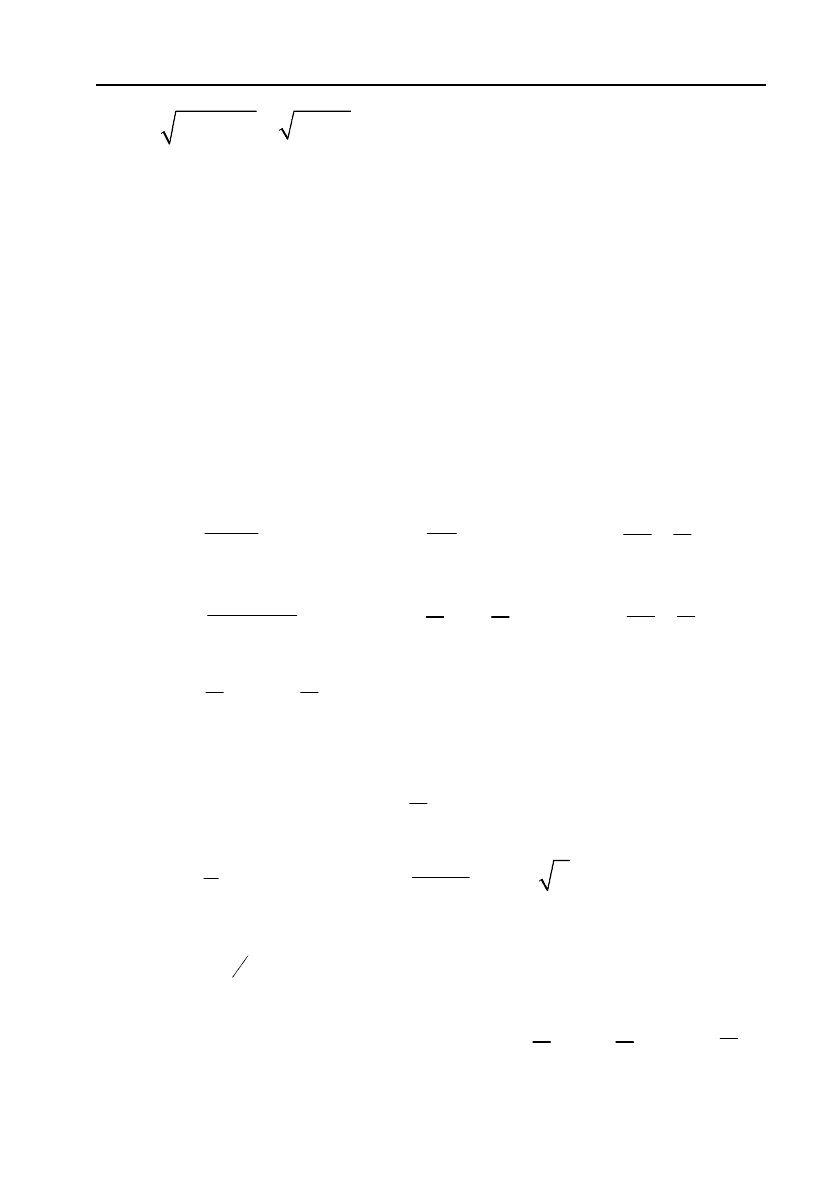
371

Частина 12. Звичайні диференціальні рівняння

110ydx xdy

;f)



110ydx xdy

;

cos ctg 0ydx xdy 

Знайти загальний розв’язок лінійних диференціальних рівнянь

першого

порядку:

а)





;b)

sin





;

с)

yyx





;d)



14 3xyxy





;





;f)

xy y





;

yyx







Знайти загальний розв’язок однорідних диференціальних

рівнянь

першого порядку:







; b)





; c)





;







; e)





; f)





;

sin











Знайти загальний розв’язок рівняння Бернуллі:

а)

22 3

1xy y xy



 

; b)





; с)

ln 0xy y x y



 

;

yyy





; e)

yxy







Знайти розв’язок задачі Коші:

а)







20y 

;b)

yye







11y 

;

с)







01y 

;d)

sin











;

372

Барковський В.В., Барковська Н.В. «Вища математика для економістів»









11y 

Знайти загальний розв’язок диференціального рівняння друго!

го порядку:

а)

 



; b)



20yy y

 

 

; с)



10xy y

 

 

;

yyxe

 



; e)



20yyy



 

 

Знайти загальний розв’язок рівняння:

а)





; b)

430

yyy

 



; с)

yy y

 

 

;





; е)

230

yyy

 



; f)

yyy

 



Розв’язати задачі економічного змісту:

а) Швидкість зростання кількості населення пропорційна

кількості

населення. Знайти закон зростання населення держави, в

якій

у 1990 р. було 50 млн. населення. Яка кількість населення буде

2000 р.?

Відносно попиту кількості одиниць

певного товару варті!

стю

за кожну одиницю відомо, що еластичність попиту, яка виз!

начається формулою





, постійна і дорівнює



. Знайти

функцію

попиту на цей товар.

с) Еластичність попиту на деякий товар постійна і дорів!нює



2

. Визначити функцію попиту вигляду



fx

, якщо

p 

коли

4x 

Еластичність попиту на певні вироби змінюється разом із

зміною

вартості кожного виробу за законом







Визначити функцію попиту вигляду



fx

, якщо

010





, коли

15x 

373

Частина 12. Звичайні диференціальні рівняння

e) Кількість населення деякого міста



(

вимірюється рока!

ми) задовольняє диференціальному рівнянню



0,1 1 10

yy y







Через скільки років населення цього міста зросте з 100 000 до

500 000?

Еластичність попиту товару

200x







. Визначити функцію

попиту

вигляду



x

, якщо

0 200x



, коли

190x 

Інвестиція величиною 10 тисяч гривень зростає неперервно із

швидкістю

пропорційною 5%. Знайти:

значення інвестиції у довільний час

;

чому буде дорівнювати інвестований капітал через 8 років?

через скільки років інвестиція буде дорівнювати 20 тисяч гри!

вень?

температура

охолодження тіла змінюється за законом



kT T



де

– температура навколишнього середовища.

Знайти формулу для



у випадку, коли

постійна і



0TT

374

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

Частина 13

ЧИСЛОВІ ТА СТЕПЕНЕВІ РЯДИ

Методи інтегрування, викладені у частині 10, можна розглядати

як

обґрунтування таблиці інтегралів (наприклад, таблиці 6 додатку).

Частина 13 може розглядатись як обґрунтування таблиць значень

експоненціальних

функцій



, логарифмічних функцій (наприк!

лад, таблиць 2 і 3 додатку). Наближені значення цих функцій часто

використовують

при розв’язуванні задач, в тому числі і економічно!

го змісту. Крім того, методи цієї частини застосовуються до: знаход!

ження наближених значень інтегралів, які часто зустрічаються в теорії

імовірностей

та у страховій справі і не можуть бути виражені еле!

ментарними функціями; при розв’язуванні диференціальних рівнянь.

Відомо, що найкращими таблицями, якими користуються в усіх

країнах

біля 100 років, є чотиризначні математичні таблиці В.М.Бра!

діса, бо наведені у цих таблицях значення функцій знайдені з точн!

істю до п’ятого знаку. Ці таблиці складались декілька років студен!

тами першого та другого курсів під керівництвом професора

.М.Брадіса з використанням понять, ознак та формул, з якими ми

ознайомимось

у цій частині.

13.1. Числові ряди

13.1.1. Загальні поняття

Нехай

задана нескінченна послідовність чисел

123

,,,,,

aaa a

Вираз

123 n

aaa a



називають нескінченним число

вим рядом

, числа

123

,,,,,

aaa a

— членами ряду,

— за

гальним членом цього ряду

Отже, від послідовності ми перейшли до ряду.

За допомогою знака суми ряд можна записати так:

375

Частина 13. Числові та степеневі ряди







де

приймає значення від 1 до



Щоб задати числовий ряд, треба задати його загальний член

у вигляді формули



afn

за якою для будь!якого

можна знайти відповідний член ряду.

Наприклад, нехай загальний член ряду





, тоді відповід!

ний ряд буде:

12 3

2510 1

   





або









Іноді задають декілька перших членів ряду і треба записати увесь

ряд

, тобто знайти його загальний член.

При цьому треба знаходити загальний член ряду по можливості

простішого

вигляду.

Наприклад, знайти загальний член ряду

234

11 1 1

222 32 42







Маємо: перший член ряду

a 

, другий член ряду

a 



a 



a 



. Отже, шукана функція повинна мати вигляд

дробу

, чисельник якої дорівнює 1, а знаменник повинен дорівнюва!

ти

n

, тобто загальний член заданого ряду буде





а ряд має вигляд









376

Барковський В.В., Барковська Н.В. «Вища математика для економістів»



Означення 1. Частковою сумою числового ряду (1) назива&

ють суму

перших т членів цього ряду, тобто

212

Saa

;

3123

Saaa

; ...;

12mm

Saa a





Означення 2. Сумою

числового ряду







називають гра&

ницю його часткової суми

при

n 

, тобто

lim lim

SS a

 







. (2)



Означення 3. Якщо границя часткової суми ряду є скінчене

число

, то ряд називають збіжним і позначають цей факт так:









Якщо границя часткової суми не існує або дорівнює



, то число&

вий ряд називають розбіжним.



Означення 4. Числовий ряд вигляду

121

aq a aq aq aq







    





(3)

називають рядом геометричної прогресії із знаменником

та пер

шим членом



Приклад 1. Дослідити збіжність ряду геометричної прогресії.



Розв’язання. При

1q 

часткова сума

визначається за відо!

мою формулою суми спадної геометричної прогресії:

aaq







Тому сумою ряду у цьому випадку буде

377

Частина 13. Числові та степеневі ряди

lim lim

11 1

aaq a

qq q

 



 



 



тобто ряд збігається та його сума





Якщо 1q  , то частковою сумою ряду буде

aq a







, а сума

ряду



lim lim 1

SS q

 

 



тобто ряд розбігається.

Якщо

1q 

, то

Saa ana 



, тому сума ряду буде

lim lim

SS na

 



тобто ряд розбігається

Якщо

1q 

, то

Sa

0S 

Sa

0S 

, ...

Послідовність таких часткових сум границі не має (вона залежить

вік

способу прямування

до



), тому ряд розбігається.

Отже, ряд геометричної прогресії збігається при

1q 

і розбі!

гається при

1q 



Означення 5. Числовий ряд вигляду

111 1

ppp p





    





(4)

називають узагальненим гармонічним рядом.

Математиками доведено, що при



узагальнений гармоніч!

ний ряд розбігається, а при



цей ряд збігається.

При



ряд (4) приймає вигляд

378

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

13.1.2. Деякі властивості числових рядів

Нехай

задано числовий ряд

123 1 2nn nm

aaa a a a

 

   



(1)

Якщо в цьому ряду відкинути перші

членів, то одержимо ряд,

який називають залишком ряду (1) після

&го члена і позначають

тобто

12nn n nm

ra a a

 

 



(6)



Теорема 1. Якщо ряд (1) збігається, то збігається і його

залишок, і, навпаки, якщо збігається залишок, то збігається й

ряд (1).

Доведення

. Нехай ряд (1) збігається. Розглянемо часткову суму

nm

членів ряду



nm n n n nm

SSaa a



  



. (7)

Зафіксуємо номер

і нехай

m 

. Тоді границя



, існує

за

умовою і дорівнює сумі ряду

При фіксованому

є постійне число, тому границя



nn nm

aaa

 

 

при

m 

існує і дорівнює

. Отже,

SS r

(8)

Нехай тепер залишок збігається. Доведемо, що ряд також збігаєть!

ся. Знову в рівності (7) зафіксуємо

та перейдемо до границі при

m 

. Границя існує тому, що за умовою залишок збігається, а

часткова

сума

при фіксованому

є постійне число. Отже, гра!

ниця

1111 1

234





 





(5)

і називається гармонічним рядом. Цей ряд розбігається.

379

Частина 13. Числові та степеневі ряди

lim

nm n n

SSr







Із рівності (7) випливає: якщо ряд (1) розбігається, то і залишок

розбігається

, і, навпаки, якщо залишок розбігається, то ряд також

розбігається

Із рівності (8) випливає, що

rSS

, тому при

n 

зали!

шок збіжного ряду

r 



Наслідок. Якщо в ряді (І) суму перших п членів відкинути, то

це

не вплине на збіжність чи розбіжність ряду.



Теорема 2. Якщо члени збіжного ряду







помножити на

число

, то одержаний ряд







також буде збіжним, а його

сума помножиться на



Теорема 3. Якщо ряди







та







збігаються, то ряд











також збігається, причому сума останнього ряду до

рівнює

SS S

, де













Доведення

теореми 2 та теореми 3 випливає із означення

збіжності

числового ряду та властивостей границі.

380

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

13.1.3. Необхідна ознака збіжності ряду



Теорема 4. Якщо ряд







збігається, то його загальний

член

a 

при

n 

, тобто

lim 0





. (9)

Доведення. Дійсно,

1nnn

aSS





, звідси одержимо



lim lim lim lim 0

nnn nn

nn nn

aSS SSSS



   

    

що й треба було довести.

Якщо умова (9) не виконується, то числовий ряд розбігається.

Наприклад, ряд









розбігається тому, що

lim lim lim 1

nn n

  





Відмітимо, що умова збіжності (9) є лише необхідною умовою.

Так, гармонічний ряд







задовольняє умову (9), але цей ряд роз!

біжний.

13.1.4. Достатні ознаки збіжності додатних числових рядів

більш повних курсах вищої математики доведені слідуючі до!

статні ознаки збіжності додатних числових радів, які бажано зрозу!

міти та використовувати.



Ознака порівняння. Нехай треба дослідити збіжність задано&

го ряду









. (10)