Бауэр Ф.Л., Гооз Г. Информатика. Том 1

Подождите немного. Документ загружается.

2.2. Формулы

111

с Необлагаемая налогом часть

дохода

(300 марок, на супруже-

скую пару 600 марок)

Доходы

от сдачи внаём и в аренду

7. Прочие

доходы

а Сумма

доходов

(при пожизненной ренте лишь соответствую-

щая

часть)

b Расходы на рекламу (максимум на общую

сумму

200 марок)

8. Сумма, не облагаемая возрастным налогом, для родившихся до

2 1 1917

а Полная заработная плата, не считая

доходов

от социального

обеспечения

b Сумма положительных величин под номерами с 1 по 3 и с 5

по

7 (но не считая

дохода

от пожизненной ренты)

9. 40 % итоговой суммы, но не больше

3000

марок на каждого из

супругов

[Всё — в марках ФРГ. В оригинальном формуляре все пояснения даны прямо

на

бланке в соответствующих строках. — Изд. ред 1

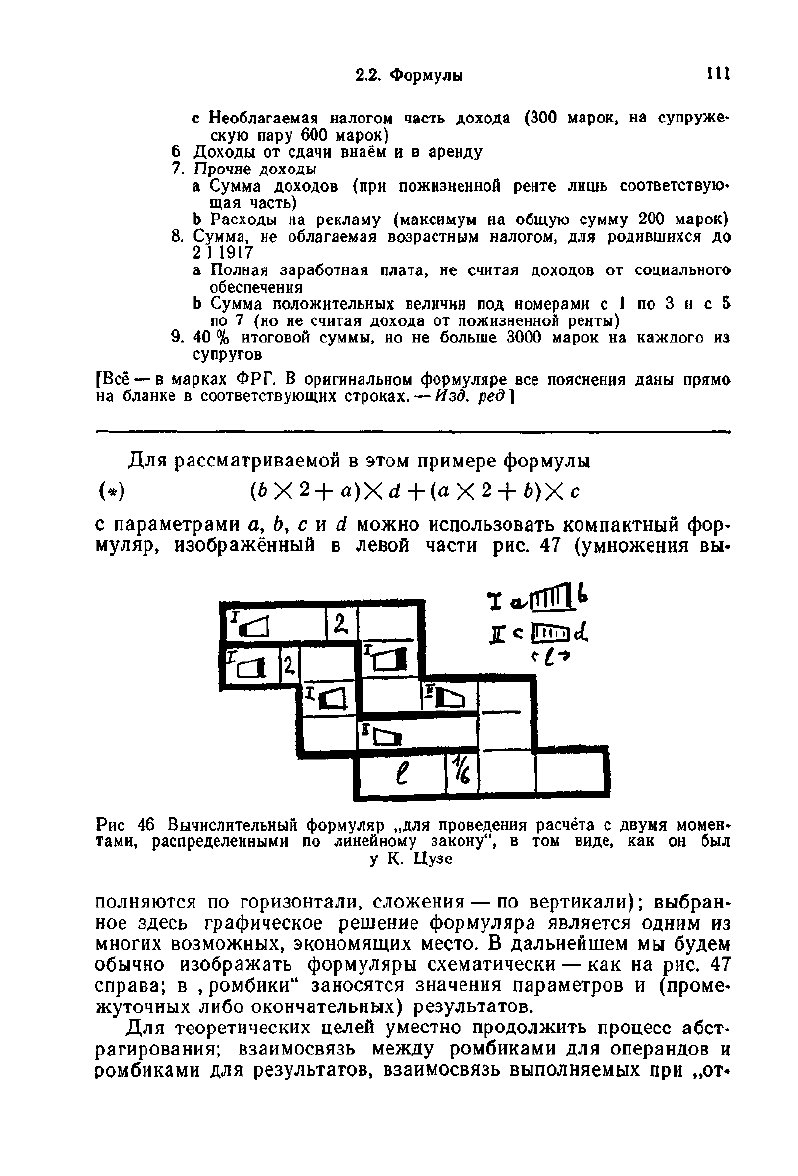
Для рассматриваемой в этом примере формулы

с параметрами а, Ь, с и d можно использовать компактный фор-

муляр, изображённый в левой части рис. 47 (умножения вы-

'а

:галП1П>

Рис

46 Вычислительный формуляр „для проведения расчёта с двумя момен-

тами, распределенными по линейному закону", в том виде, как он был

У К. Цузе

полняются

по горизонтали, сложения — по вертикали); выбран-

ное

здесь графическое решение формуляра является одним из

многих возможных, экономящих место. В дальнейшем мы

будем

обычно изображать формуляры схематически — как на рис. 47

справа; в ,ромбики" заносятся значения параметров и (проме-

жуточных либо окончательных) результатов.

Для теоретических целей уместно продолжить процесс абст-

рагирования;

взаимосвязь

между

ромбиками для операндов и

ромбиками

для результатов, взаимосвязь выполняемых при „от-

112

Гл. 2 Основные понятия программирования

работке" формулы подстановок выражается топологически '•

деревом

Канторовича

или

схемой

потока

данных

отвечаю-

щими

данной формуле (обычно они изображаются так, как по-

казано

на рис. 48).

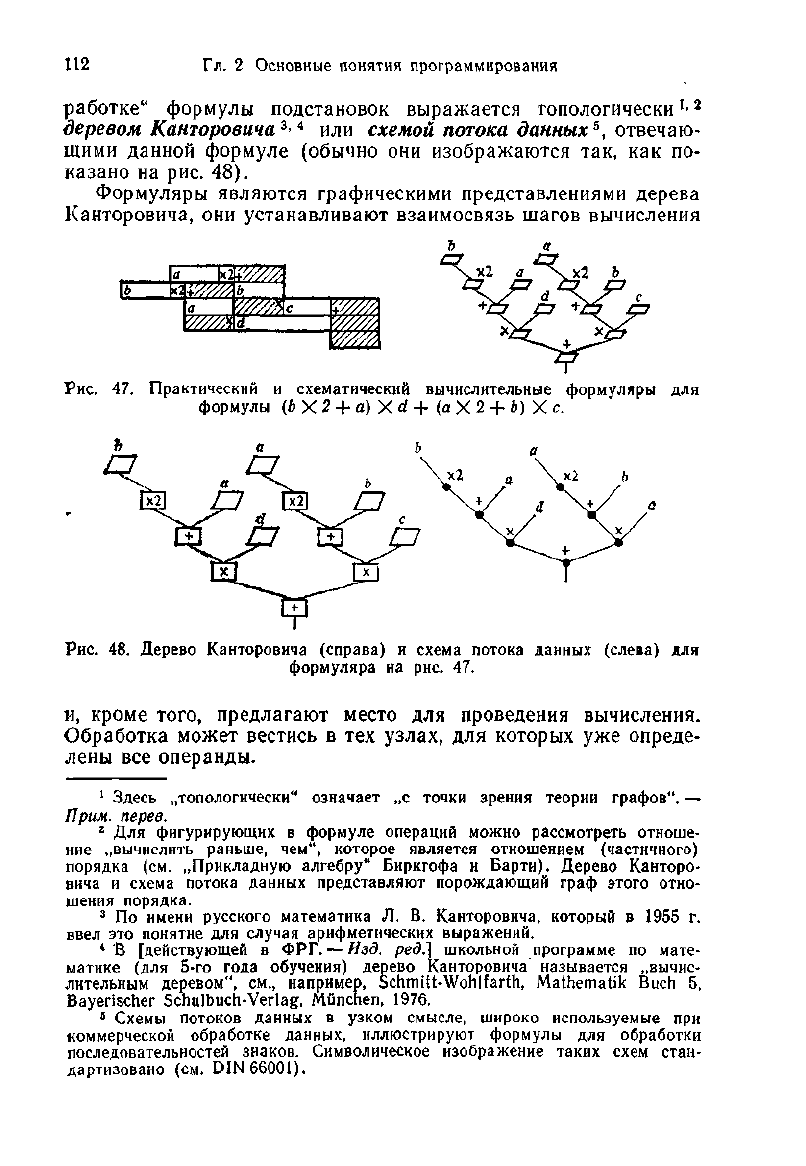
Формуляры являются графическими представлениями дерева

Канторовича,

они устанавливают взаимосвязь шагов вычисления

У////Л

ШУЯ с

у/////.

У////Л

Рис.

47. Практический и схематический вычислительные формуляры для

формулы

(Ь

X 2 + а) X d + (а X 2 +

Ь)

X с.

Рис.

48. Дерево Канторовича (справа) и

схема

потока данных (слева) для

формуляра на рис. 47.

и,

кроме того, предлагают место для проведения вычисления.

Обработка может вестись в тех

узлах,

для которых уже опреде-

лены все операнды.

Здесь „топологически" означает „с точки зрения теории графов". —

Прим.

перев.

Для фигурирующих в формуле операций можно рассмотреть отноше-

ние

„вычислить раньше, чем", которое является отношением (частичного)

порядка (см. „Прикладную

алгебру"

Биркгофа и Барти). Дерево Канторо-

вича и

схема

потока данных представляют порождающий граф этого отно-

шения

порядка.

По имени русского математика Л. В. Канторовича, который в 1955 г.

ввел это понятие для случая арифметических выражений.

В [действующей в ФРГ. — Изд. ред.] школьной программе по мате-

матике (для 5-го

года

обучения) дерево Канторовича' называется „вычис-

лительным деревом", см., например, Schmitt-Wohlfarth, Mathematik Buch 5,

Bayerischer

Schulbuch-Verlag,

Munchen, 1976.

Схемы потоков данных в узком смысле, широко используемые при

коммерческой обработке данных, иллюстрируют формулы для обработки

последовательностей знаков. Символическое изображение таких

схем

стан-

дартизовано (см. DIN

66001).

2.2. Формулы

113

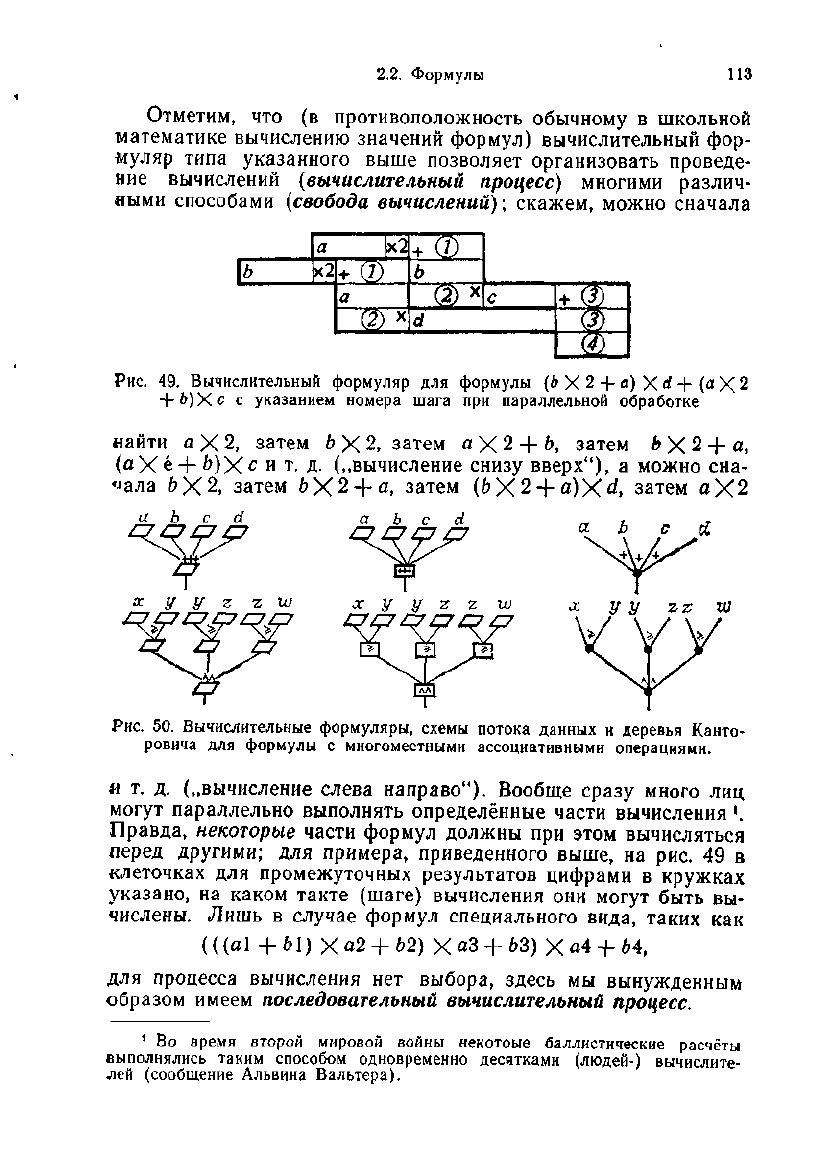
Отметим,

что (в

противоположность обычному

школьной

математике вычислению значений формул) вычислительный

фор-

муляр типа указанного выше позволяет организовать проведе-

ние

вычислений

{вычислительный процесс)

многими различ-

ными

способами

(свобода вычислений);

скажем, можно сначала

(

Рис.

49.

Вычислительный формуляр

для

формулы

(Ь X 2 + а) X d + (а X 2

Ь)Хс с

указанием номера шага

при

параллельной обработке

найти

а X 2,

затем

b X 2,

затем

с X 2 + й,

затем

6 X 2 + а,

(аХе

+ Ь)Х

с и т

- Д-

(„вычисление снизу вверх"),

можно

сна-

чала

6X2,

затем

ЬХ% + а,

затем

(6X2 + a)Xd,

затем

гг Ю

Рис.

50.

Вычислительные формуляры, схемы потока данных

деревья Канто-

ровича

для

формулы

многоместными ассоциативными операциями.

т. д.

(„вычисление слева направо"). Вообще сразу много

лиц

могут

параллельно выполнять определённые части вычисления

Правда,

некоторые

части формул должны

при

этом вычисляться

перед другими;

для

примера, приведенного выше,

на рис. 49 в

клеточках

для

промежуточных результатов цифрами

кружках

указано,

на

каком такте (шаге) вычисления

они

могут

быть

вы-

числены.

Лишь

случае

формул специального вида, таких

как

(((а\

+ Ы) Ха2 + Ь2) ХаЗ +

ЬЗ)

Ха4 + Ь4,

для процесса вычисления

нет

выбора, здесь

мы

вынужденным

образом имеем

последовательный вычислительный процесс.

Во

время второй мировой войны некотоые баллистические расчёты

выполнялись

таким способом одновременно десятками (людей-) вычислите-

лей (сообщение Альвина Вальтера).

114

Гл. 2. Основные понятия программирования

В общем

же

случае

формулы обычно допускают совместное

вычисление

(см. 1.6.1); в

частности,

так

обстоит дело, когда

них встречаются многоместные ассоциативные операции

(рис.

50).

Части вычислительного процесса, которые

могут

вы-

полняться

параллельно, называются

подпроцессами.

2.2.2.3.

Строгость операций

Прежде всего резюмируем сказанное выше относительно

вы-

числения

значений формул:

результат

формулы, которая

не

сводится

обозначению

па-

раметра

или

стандартному обозначению, определяется рекур-

сивно:

он

получается применением доминирующей операции

формулы

результатам формул-операндов.

Поэтому

результат

формулы останется

тем же

самым, если

некоторую подформулу заменить

на её

результат.

При

этом

та или

иная операция вполне может обладать

тем

свойством,

что (в

определённых

случаях)

её

результат

можно»

Рис.

51.

Дерево Канторовича

для

формулы sin(x)X,(y/x).

указать

ещё до

того,

как

станут известны

все

операнды.

Так,

например,

результат

умножения

>левая

формула <Х> правая формула<

уже известен, если вычислен

результат

клевой формулы<

и ока-

залось,

что он

равен нулю;

этом

случае

результат

жравой

формульк можно вообще

не

вычислять. Аналогично обстоит

дело

конъюнкцией

дизъюнкцией высказываний.

Особая обработка такого рода ситуаций должна проводиться

не

„тайком",

явно,

посредством надлежащего разбора случаев.

Соответствующие средства

будут

введены

2.2.3.

связи

этим

сформулируем следующий принцип:

Все базовые операции используемых вычислительных струк-

тур должны быть

строгими,

т. е. при их

применении

вычисли-

тельных формулярах

при

всех

обстоятельствах должны вычис-

ляться

все их

операнды.

При

этом

не

только, скажем, формула

1/0

2.2. Формулы

115

не

имеет определённого результата (операция

.'/.

является

ча-

стично определённой,

см.

2.1.3.3),

но и

результат

формулы

ох

(I/O)

не

определён; вычислигзльный формуляр

для

формулы

sinWX

Ху/х)

деревом Канторовича, представленным

на рис. 51, при

= 0 не

даёт

никакого результата.

2.2.2.4.

Преобразование формул

Если

применить

формуле, которая определена

над

некото-

рой

вычислительной структурой, какие-либо законы этой струк-

туры,

то

получится

эквивалентная

формула, которая определяет

то

же

самое отображение

Обычно преобразованной формуле

(несмотря

на её

эквивалентность исходной) отвечает

другой

вы-

числительный формуляр,

а с ним и

другое

дерево Канторовича.

Иногда

эти

изменения незначительны,

как

будет,

например,

случае, если приведённую выше формулу

(*) над Z с

помощью

закона

коммутативности преобразовать

виду

Формуле

(*)

эквивалентны также (получаемые

при

использо-

вании

закона дистрибутивности

в Z)

формула

(отличающаяся

от

исходной лишь взаимной заменой

Ь на с и а

на

d) и

формула

(а

X с +

X d) X 2 +

(а

X d +

X с)

с одним дополнительным умножением, вычислительный форму-

ляр

для

которой изображён

на рис. 52.

точки зрения возможностей параллельной работы пред-

ставляет интерес нахождение

для

заданной формулы

не

только

эквивалентной

ей

формулы

наименьшим числом операций,

но

формулы, которая допускает вычисление

за

наименьшее число

вычислительных шагов (тактов).

Для

вычисления значения

по-

линома

х*

а\х

+ а

х + а

имеется формула

(((а0Х

х + а\)Х х + а2)Х х+ аЗ)Х х+ а4,

Эквивалентность формул включает

себя также

совпадение обла-

стей определения соответствующих отображений. Формула

х X (у/х) над

\ {0} и

формула

у над Z не

эквивалентны!

116

Гл. 2. Основные понятия программирования

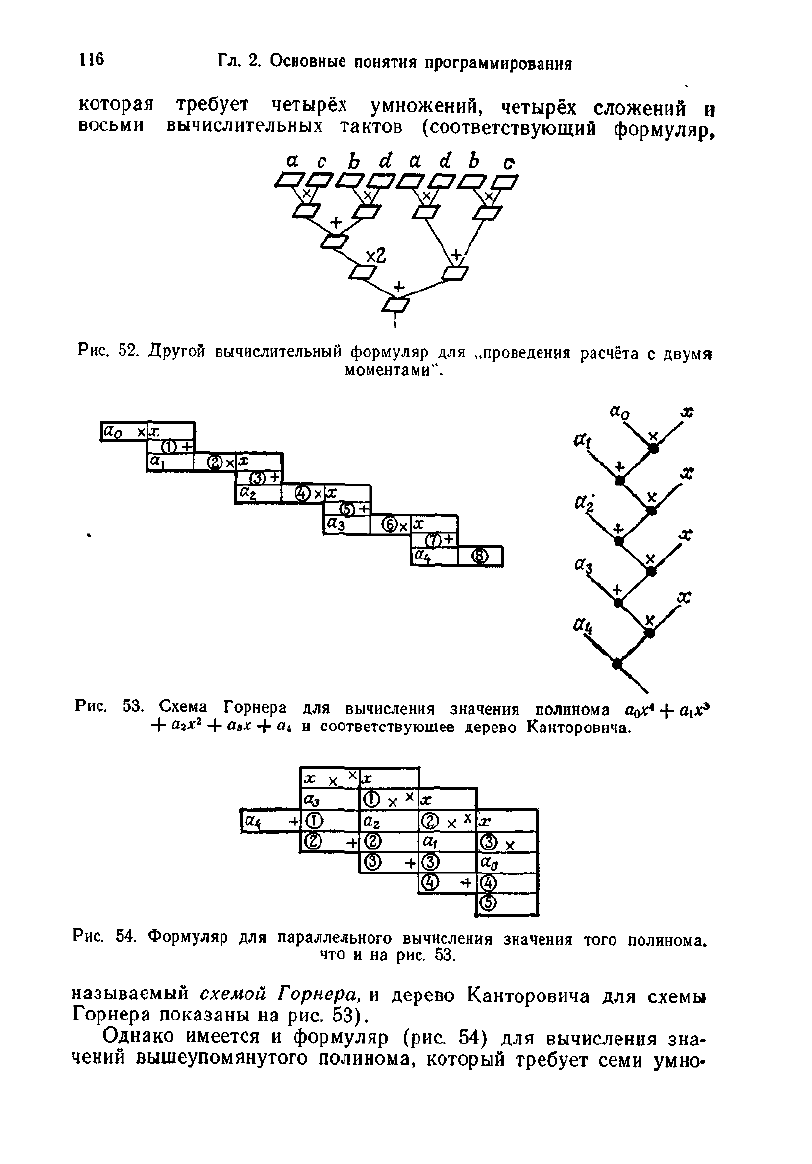
которая

требует

четырёх умножений, четырёх сложений и

восьми вычислительных тактов (соответствующий формуляр,

а с Ъ d a. d Ъ о

Рис.

52. Другой вычислительный формуляр для „проведения расчёта с двумя

моментами".

©хх

(51

Рис.

53. Схема Горнера для вычисления значения полинома

х*

пгх

-\- азХ + а

и соответствующее дерево Канторовича.

©X

® +

CD +

® X

Рис.

54. Формуляр для параллельного вычисления значения того полинома,

что и на рис. 53.

называемый

схемой

Горнера,

и дерево Канторовича для схемы

Горнера показаны на рис. 53).

Однако имеется и формуляр (рис. 54) для вычисления зна-

чений

вышеупомянутого полинома, который

требует

семи умно-

2.2.

Формулы

117

жений

и четырёх сложений, но зато

даёт

значение полинома

всего за пять вычислительных тактов (на полях промежуточных

результатов указано цифрами в кружках, на каком наименьшем

такте этот

результат

может быть вычислен). Обобщение на по-

линомы

произвольной степени является очевидным '.

Способ формального описания таких формуляров с много-

кратным

применением промежуточных результатов мы изучим в

3.1.1.

2.2.3.

Условные

формулы

Если

помимо композиции операций ввести в игру ещё и раз*

бор случаев, то мы получим

условные

формулы.

2.2.3.1.

Альтернатива

последовательный

разбор

случаев

Простейший

разбор случаев — это

альтернатива

которая

состоит из

двух

подформул —

да-формулы

нет-формулы,

одна

из

которых и подлежит обработке (говорят также о

двух

ветвях

альтернативы).

Выбор выполняется на основе результата, вырабатываемого

некоторой

другой

формулой — некоторым высказыванием, кото-

рое называется

условием.

Вырабатываемым результатом усло-

вия

является значение истинности, т. е. либо Т (и

тогда

„вы-

бери да-формулу"), либо F („выбери нет-формулу"). Таким

образом, условные формулы имеют следующий вид:

if >условиес

then

>да-формула<

else

>нет-формулас fi

(алгол-68)

или

(>условие<-»ода-формула>; Т-*>нет-формула<) (лисп)

Фигурирующие здесь символы if,

then,

else

и fi

служат

дальней-

шими

примерами использования словесных символов.

Имеются схемы каскадного типа, для которых число тактов пропор-

ционально

лишь логарифму степени полинома.

Называемая также

бинарным

разбором

случаев.

(Правильнее было бы

говорить о

диадическом

разборе

случаев

[см. первое подстрочное примечание

в разделе

2.1.3.5.

— Изд.

ред.].)

В русскоязычной версии алгола эта формула выглядит так:

если >условие< то >формула-ТО<

иначе

>формула-ИНАЧЕ<

всё.

Здесь

если,

то,

иначе-

дословные переводы соответствующих английских

слов, а вместо fi (if „наоборот") поставлено не

илсе,

всё.—

Прим.

изд. ред:

Т стоит вместо »истина«; последовательная редакция этой формулы

дана

ниже.

118

Гл. 2.

Основные понятия программирования

В качестве да- или нет-формул (как и в качестве условия)

•могут

стоять как (простые) формулы, так и условные формулы:

Условные

формулы

сами

являются

формулами.

Примеры

(с параметрами подходящего сорта):

(1) if х > О

then

else

— х fi,

(2) if a

then

else

0 fi,

^3) if tn > n

then

else

n fi,

<4)

if x>0

then

else

(if *>0

then

else

-1 fi) fi.

Стало быть, с помощью разбора случаев операции взятия абсо-

лютного значения, максимума (минимума) и знака

могут

быть

сведены к другим операциям над целыми, соответственно над

вещественными числами. При опускании скобок (они не нужны)

последний пример принимает вид

if x>Q

then

else

if x> О

then

else-

1 fi fi.

Таким

образом, разбор случаев с более чем двумя ветвями мож-

но

реализовать с помощью вложенных альтернатив.

Для того частного случая вложения, когда, как в послед-

нем

примере, каждый раз (если не считать самого конца) в

нет-случае ставится новое условие и потому все завершающие

fi сосредоточиваются у правого края

(последовательный

разбор

случаев)

вводится сокращенная форма записи (else if „стяги-

ваются" до

elsf),

скажем для вышеприведённого примера

if JC>0

then

elsf

*>0

then

else

—1 fi (алгол-68)

(отметим, что при этом все внутренние fi опускаются} или

(*>0->1;

х>0->0; Т->-1) (лисп).

В паскале завершающее fi опускается, но есть

возможность

„расставить скобки" с помощью

словарных

скобок

begin

и end

begin

if >условие<

then

>да-формула<

else

>нет-формула< end.

Обычные правила применения продукций

алгоритмах Маркова также

Приводят

последовательному разбору случаев.

Begin

• -

начало,

end

- конец.

—

Прим.

изд. оед.

2.2. Формулы 119

Это верно и для последовательного разбора случаев, при кото-

ром

else

If не стянуты в

elsf.

Примеры:

begin if x > 0 then x

else

—x end (паскаль),

begin if x>0 then 1

else

if *>0 then 0

else

—1 end

(паскаль).

В стандартном паскале, однако, условные формулы, строго го-

воря,

не предусмотрены, в частности их нельзя подставлять в

другие формулы. Однако условные формулы запрятаны за та-

кими

конструкциями, как

begin if >условие< then >Res< <= >да-формула<

else

>Res< -<= >нет-формула< end,

где >Res< — это обозначение

результата,

см. 2.3.1.1.

Само

собой разумеется, что обе ветви альтернативы, да-

формула и нет-формула, должны иметь результат одного и

того же сорта (вида, типа), и тогда условная формула приво-

дит к тому же сорту. Далее, очевидно, что формуле

if >условие< then >да-формула<

else

>нет-формула< fi

эквивалентна

формула

>условие< then >нет-формула<

else

>да-формула< fi

(перестановка

ветвей

альтернативы при отрицании условия).

Пример

лг + if х > 0 then x

else

— x fi

показывает, что условные формулы

могут

выступать как со-

ставная часть (простой) формулы — правда не в паскале.

Впрочем, такие формулы можно преобразовать к „обычному"

виду, перенося соответствующую операцию (это возможно, по-

скольку все операции у нас строгие) в да-формулу и в нет-фор-

мулу:

if х > 0 then х + х

else

х — х fi.

Применение

законов из вычислительной структуры Z даёт

окончательно

if x>0 then хХ%

else

0 fi.

При

работе с объёмистым, обширным разбором случаев — осо-

бенно

вложенного типа — весьма полезен так называемый „ме-

тод таблиц решений". Этому подходу близок (а функциональ-

но

тождествен) подход с использованием двузначных схем

(„алгебра схем"), см. гл. 4.

120

Гл. 2.

Основные понятия программирования

2.2.3.2.

Охраняемый разбор случаев

Альтернатива является частным (двучленным) случаем

охраняемого

(контролируемого,

защищаемого) разбора случаев

€

ветвями:

if >условие

1< then

>формула

[] >условие

2< them

формула

[] >условие

m then

>формула

m fi,

при

котором перед каждой формулой ставится некоторое

условие, называемое

охраняющим, или защищающим, или ко-

ротко

—

стражем.

Альтернативе

if >условие(

then

>да-формула<

else

>нет-формула<

fi,

эквивалентен

охраняемый разбор случаев

двумя ветвями

if >условие<

then

>да-формула<

[] ~1 >условие<

then

>нет-формула<

fi.

Примеру

(1) из 2.2.3.1

соответствует охраняемый разбор

слу-

чаев

if х > 0 then х

•

х<0 then —х fi.

Трёхчленный пример доставляет операция

sign (см.

2.1.3.7

табл.

11):

if x>0 then 1

= 0 then 0

•

х<0 then -1 fi.

Порядок,

котором записываются отдельные ветви охраняемо-

го разбора случаев, неважен.

Не

говоря

уже о том, что

охра-

няемый

разбор случаев обладает поэтому совершенно симмет-

ричной

структурой

и в

явном виде предъявляет условия

для

всех

ветвей,

частности

и для

ветви

else в

случае

альтерна-

тивы,

охраняемом разборе случаев заключены принципиаль-

но

новые возможности.

именно, может случиться,

что

сразу

несколько

стражей

дадут

значение »истина«. Тогда открыт

вы-

бор

между

соответствующими формулами,

этот выбор может

быть осуществлён произвольно. Такой недетерминистиче-

ский

(см. 1.6.1)

разбор случаев может привести

формулам,