Бауэр Ф.Л., Гооз Г. Информатика. Том 1

Подождите немного. Документ загружается.

2.3.

Подпрограммы

131

fac

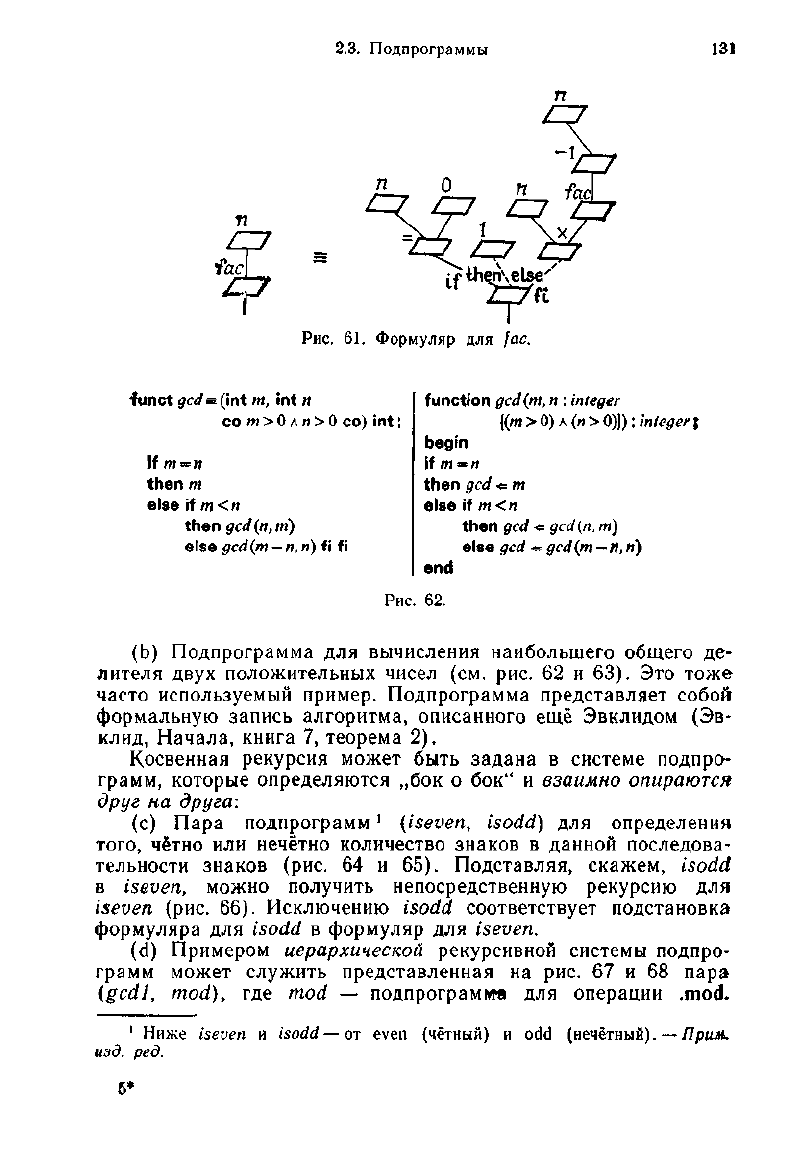
Рис.

61. Формуляр для fac.

funct

gcd=(int m, int и

сот>0ли>0

со) int:

If w = n

then

else

if m<n

then

gcd{n,m)

else

gcd(m-n,n) fi fi

function

gcd(m,

integer

((m

> 0) л (n > 0)();

integer

begin

if m = n

then

gcd « m

else

if m</i

then

gcd

gcd(n,m)

else

.^crf «

gcd(m

—n,

end

Рис.

62.

(b) Подпрограмма для вычисления наибольшего общего де-

лителя

двух

положительных чисел (см. рис. 62 и 63). Это тоже

часто используемый пример. Подпрограмма представляет собой

формальную запись алгоритма, описанного ещё Эвклидом (Эв-

клид,

Начала, книга 7, теорема 2).

Косвенная

рекурсия может быть задана в системе подпро-

грамм, которые определяются

„бок

о бок" и

взаимно

опираются

друг

на

друга:

(iseven,

isodd)

для определения

того, четно или нечётно количество знаков в данной последова-

тельности знаков (рис. 64 и 65). Подставляя, скажем,

isodd

iseven,

можно получить непосредственную рекурсию для

iseven

(рис. 66). Исключению

isodd

соответствует подстановка

формуляра для

isodd

в формуляр для

iseven.

(d) Примером

иерархической

рекурсивной системы подпро-

грамм может служить представленная на рис. 67 и 68 пара

{gcdl,

mod), где mod — подпрограмм для операции .mod.

Ниже

iseven

isodd

— от even (чётный) и odd

(нечётный).—

Прим.

изд. ред.

Б*

132 Гл.

Основные понятия программирования

•

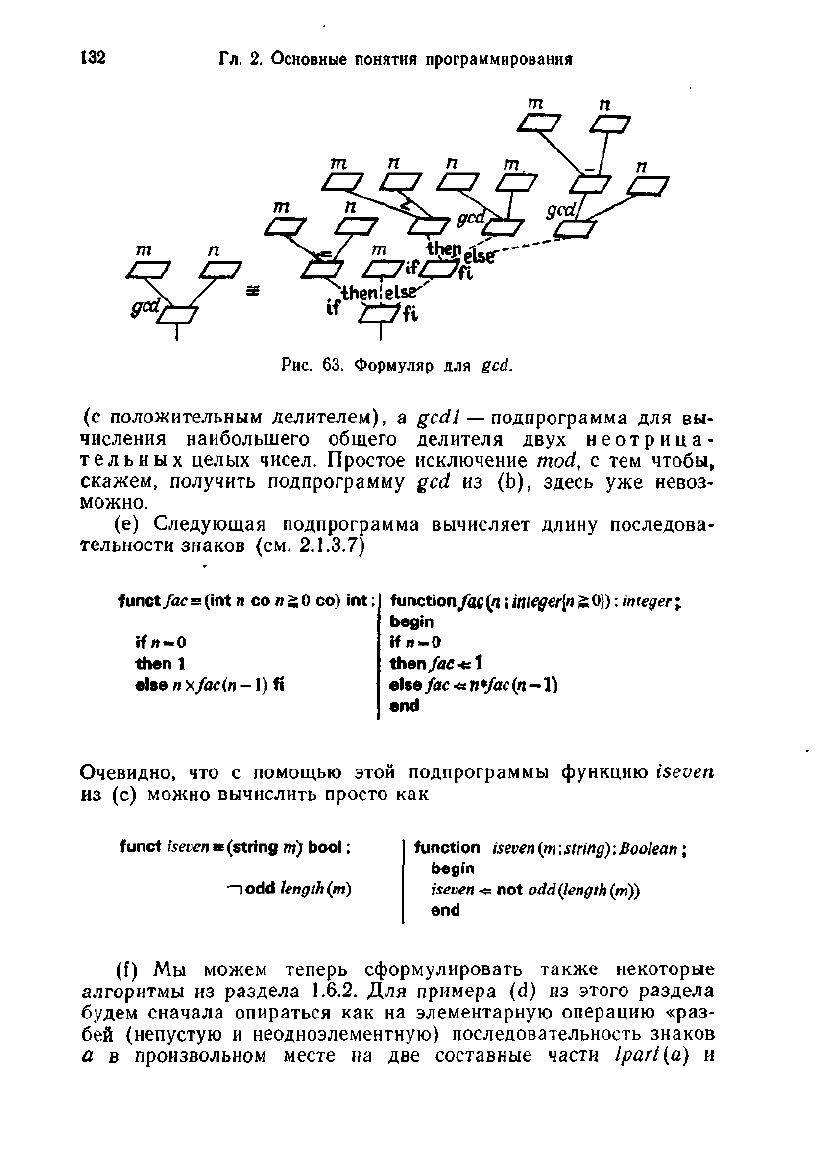
Рис.

63.

Формуляр

для gcd.

(с

положительным делителем),

gcdl

—

подпрограмма

для вы-

числения

наибольшего общего делителя

двух

неотрица-

тельных

целых чисел. Простое исключение

mod, с тем

чтобы,

скажем, получить подпрограмму

gcd из (Ь),

здесь

уже

невоз-

можно.

(е) Следующая подпрограмма вычисляет длину последова-

тельности знаков

(см.

2.1.3.7)

funet/ас

(int

n со п>0 со) int;

if n

thenl

else

nxfac(n-Y)

function/ec

(ч:

Ыедег[п

0}):

integer

begin

n»0

then

fac-*1

end

Очевидно,

что с

помощью этой подпрограммы функцию

iseven

из

(с)

можно вычислить просто

как

funct

iseven

(string

bool:

—\

odd

length

(m)

function

iseven

{m:

string):

Boolean;

begin

iseven

•<=

not

odd(length

(m))

end

(f)

Мы

можем теперь сформулировать также некоторые

алгоритмы

из

раздела

1.6.2. Для

примера

(d) из

этого раздела

будем

сначала опираться

как на

элементарную операцию «раз-

бей (непустую

неодноэлементную) последовательность знаков

а в

произвольном месте

на две

составные части Ipart(a)

2.3. Подпрограммы

133

•f

unct

iseven

(string

bool:

if/и«О

then true

else

isodd

(rest

(m)) f

funct

isodd

(string

m) boo!:

if m = О

then false

else

неуеп (rest(m)) fi

function

iseven

(m:

string):

Boolean

;

begin

isemply(m)

then

iseven

true

else

«wen

«isodd

(rest

(in))

end

function

isodd(m:

string);

Boolean;

begin

isempty

(m)

then

Morfrf

false

else

w<wW

iseven

(rest

(m))

end

Рис.

64.

ГП

Ideven

isodd

777

rest

isodd

if*

rest

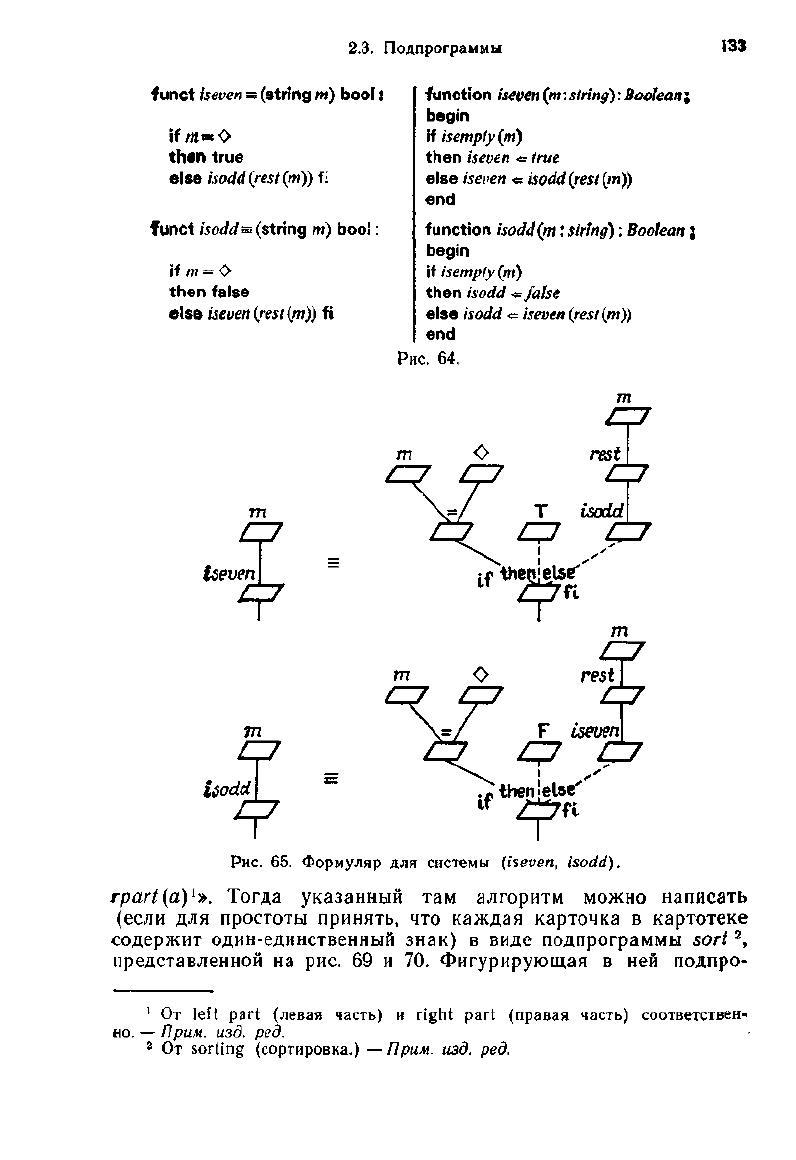
Рис.

65. Формуляр для системы

(iseven,

isodd).

rpart(a)

».

Тогда указанный там алгоритм можно написать

(если для простоты принять, что каждая карточка в картотеке

содержит один-единственный знак) в виде подпрограммы

sort

представленной на рис. 69 и 70. Фигурирующая в ней подпро-

От

left

part (левая часть) и right part (правая часть) соответствен-

но.

— Прим. изд. ред.

От sorting (сортировка.) —Прим. изд. ред.

134

Гл. 2. Основные понятия программирования

unct

iseven

(string

bool:

if/и=<>

then true

elsf

re,st(m)*=.

then false

else

iseven

(rest (rest

(m)))

function

{seven

(m:string):

Boolean

;

begin

if isempty{m)

then

iseven

•«

true

else

if isemply(rest(m))

then

faew/i

false

else

йеуея

iseven

(rest (rest

(т))У

end

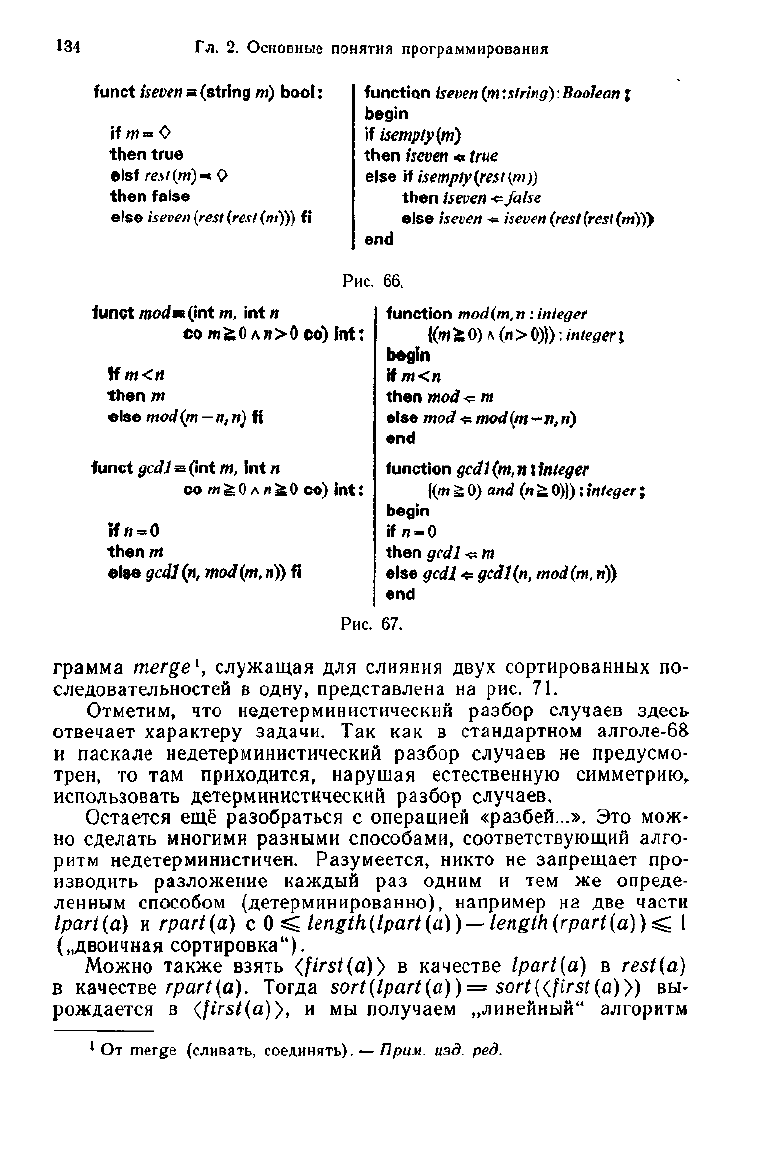
Рис.

66.

funct/nw/«E(int m, int n

сот£;0лл>0со)

Int:

!f m<n

then

else

mod(m—n,n)

unct

<?cdi = (int m, Int и

со /и а

л и SO со) int:

then M

else

grill

(p, mod(rn, n)) fi

function

mod(m, n :

integer

{(т^0)^(п>0)}):

integeri

begin

if/»<n

then

mod

•<=

else

/ио</

•<=

mod(m

—it,

end

function

^cJ/ (w, n I

integer

{(m

> 0)

a«rf

(n Ь 0)}): i

begin

if n = 0

then

gcdl

•* m

else

gcdl

gcdl(n,

mod(m, и))

end

Рис.

67.

грамма

merge

служащая для слияния

двух

сортированных по-

следовательностей в одну, представлена на рис. 71.

Отметим, что недетерминистический разбор случаев здесь

отвечает характеру задачи. Так как в стандартном алголе-68

паскале недетерминистический разбор случаев не предусмо-

трен,

то там приходится, нарушая естественную симметрию,

использовать детерминистический разбор случаев.

Остается ещё разобраться с операцией «разбей...». Это мож-

но

сделать многими разными способами, соответствующий алго-

ритм недетерминистичен. Разумеется, никто не запрещает про-

изводить разложение каждый раз одним и тем же опреде-

ленным

способом (детерминированно), например на две части

Ipart(a) и

rpart(a)

с 0 < length(Ipart(a)) —

length(rpart(a))^

(„двоичная

сортировка").

Можно

также взять

(first

(а)} в качестве Ipart (а) в

rest

(а)

качестве

rpart

(а). Тогда

sort

(Ipart (a)) =

sort

((first

(а)}) вы-

рождается в (first(а)), и мы получаем „линейный" алгоритм

От merge (сливать, соединять). — Прим. изд. ред.

2.3.

Подпрограммы

135

mpd.

" then;

else

/~7fi

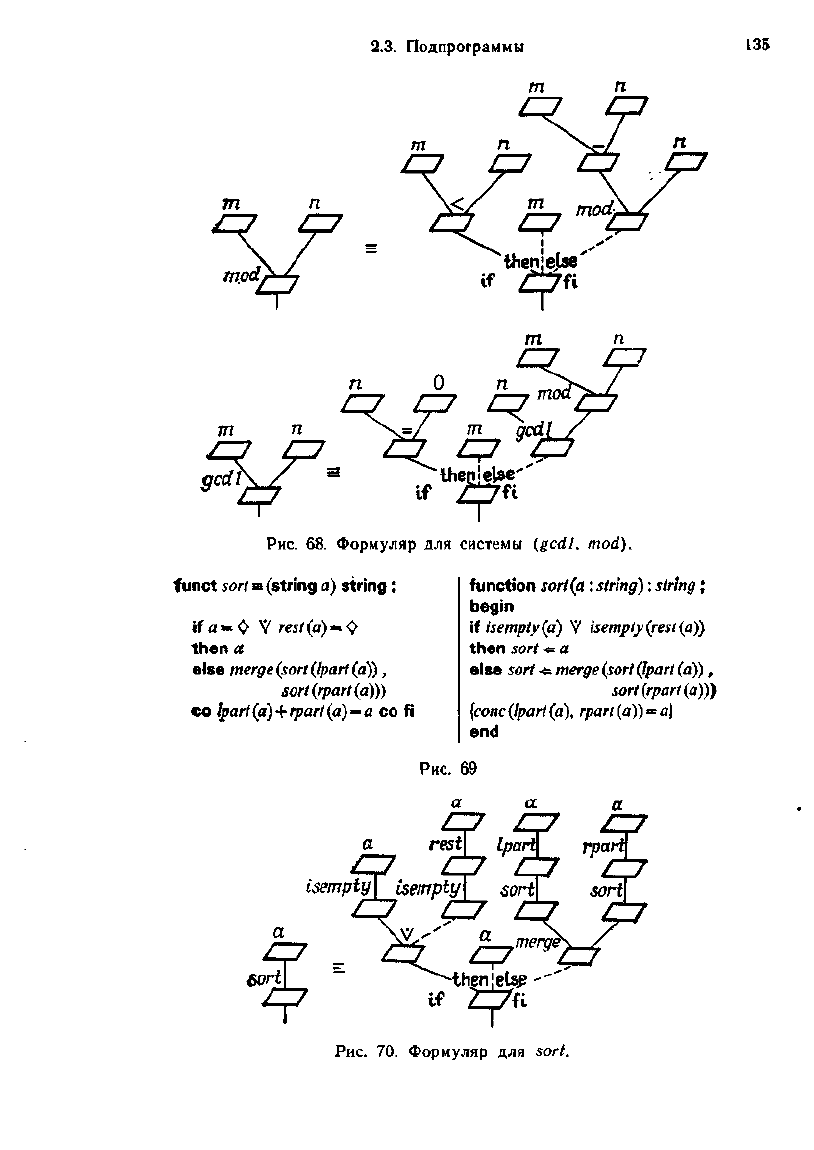
Рис.

68.

Формуляр

для

системы

(gcdl, mod).

funct sort

(string a) string :

a=<>

rest(a)=<}

then a

else

merge(sort(lpart(a)),

sort(rpart

(a)))

со

Ipart

(a)+rpart

(а)" а со fi

function sort (a: string): string;

begin

isempty

(a)

isempty(rest(a))

then sort

else

5orf * merge

(sort

(Ipart

(a)),

sort

(rpart

(a)))

[cone

(Ipart

(a),

rpart

(a)) =

end

Рис.

isempty\

isempty

sort

Рис.

70.

Формуляр

для

sort.

136

Гл.

Основные

понятия

программирования

funct

merges (string

u,v)

string:

if w=<0>

then

Dv-0

then

else M

first

(u)ufirst(v)

then

first

(u))

merge

(rest

(u)

first (u)>

first

(у)

then

0"rs/(V))-f

merge

(rest

(v),ii)

fifi

function

me^e

(i/,

v: siring):

begin

isempty(u)

then

me/ge

-*>

isempty(v)

then

merge

end

then

merge

-^prefix

(first

(u),

merge

(rest

(u),v))

first

(u)>first

(v)

then

/ие/#е

-«=

prefix

(first

(v),

merge(rest(v),u)y

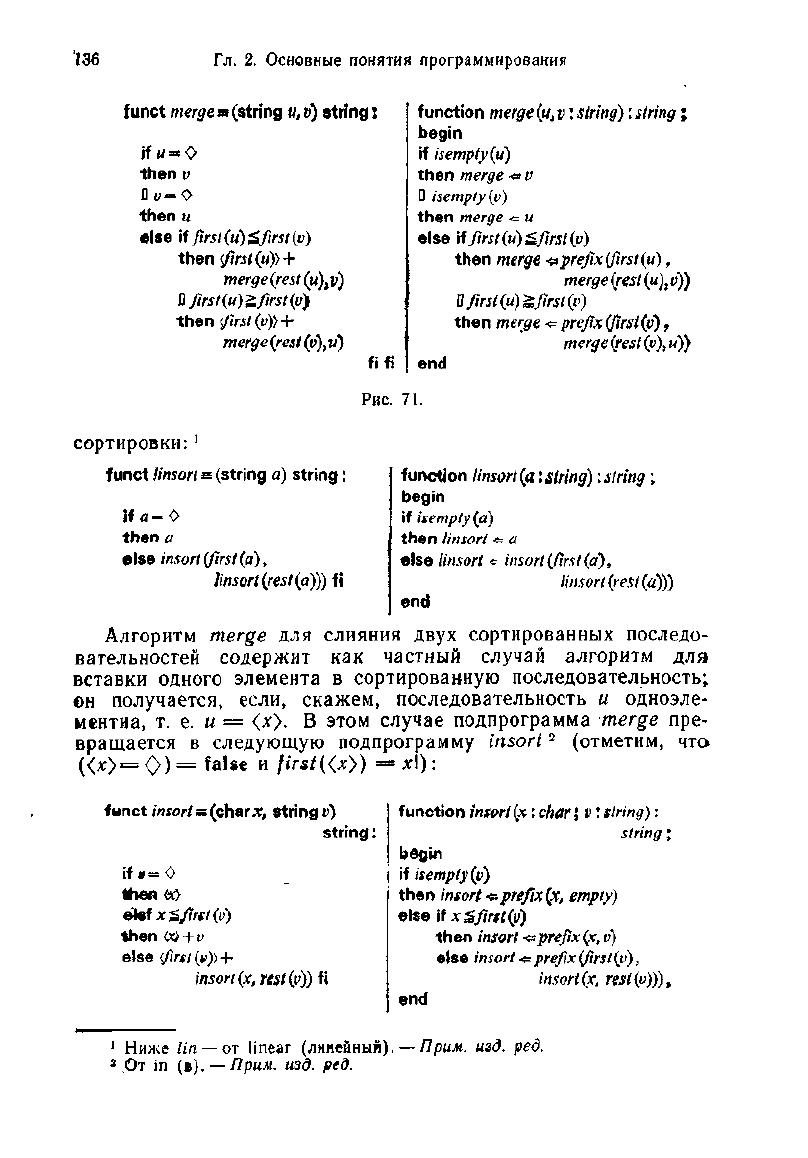
Рис.

71.

сортировки

funct

linsort

(string

string:

a=0

then

else

insort

(first

(a),

]insort(rest(a)))

function

linsort

(fl

string):

string;

begin

isemply

(a)

then

linsort

else

/w.w/

insort

(first

(a),

linsort

(rest

(a)))

end

Алгоритм

merge

для

слияния

двух

сортированных последо-

вательностей содержит

как

частный случай алгоритм

для

вставки одного элемента

сортированную последовательность;

©н

получается, если, скажем, последовательность

одноэле-

ментна,

т. е. и =

<х>.

этом случае подпрограмма

merge

пре-

вращается

следующую подпрограмму

insort

(отметим,

что

fl и

first((х})

=х\):

funct

insert

3(charx,

string и)

string:

if»=O

-then

<*>

etef

x£.firtt(v)

then

else

$/?/•«

(n)>

insort(x,rest{v))

function

insort(x;cfter;

v:string):

string;

begin

isemply

(v)

then

insort

oprefixQc,

empty)

else

\fx£fint(p)

then

iViJort

-«prefix

(x,

else insort <= prefix (first

(v),

insort

(x,

rest(y)))

end

Ниже

/in

— от

linear

(линейный).

—

Прим.

изд. ред.

От in

(в).

—

Прим.

изд. ред.

2.3.

Подпрограммы

137

Теперь

linsort

можно использовать

insert

вместо

merge,

что

даёт

funet

Hnsorlis

(string

о)

string

if a=O

then

else

merge

(first

(a)>,

linsort

(rest

(a)))

function

linsort

(a'.String)

•

string

begin

isempty(a)

then

linsort

else

linsort

merge

(prefix

(first

(a),

empty),

lms*rl(rett(*)))

end

Приведённый

примере

(е)

раздела

1.6.2

иедетерииниетичемяш

алгоритм вставки является

белее

общим.

Он

шртюмтт

к сле-

дующей подпрограмме:

funct

insort

(char

string.о)

string:

Ifp-Ф

then

Of)

«Isf

x <

first

(rpart

(v))

then

insort

(x,

Jpart(v))-t

rpart

(v)

else lpart(v) +

insort

(x,

rpart

(v))

function

insort(x:char;

V.string):

string;

begin

isemply

(v)

then

insort

•&

prefix

(x,

empty)

else

if x

first

(rpart

(v))

then

insort

•<=

cone

(insort

(x,

lpart(v))

rpart

(v))

else

insort

conc(lpart(v),

insort

(x,

rpart

(f)))

end

Снова

можно получить „линейную" редакцию алгоритма, взяв

(first(v)}

качестве Ipart(v)

res^(u)

качестве

rpart

(v); она

аналогична вышеприведенной линейной редакции.

(g) Некоторые смешанные операции,

которых говорилось

2.1.3.7,

могут быть теперь введены рекурсивным образом;

на-

пример,

операцию выбора

i-ro

знака

из

данной последователь-

ности

можно определить

так:

•

funct

sel в

(string

a, int i

со 1

length

(a)

co)char:

then

first (a)

/>1

then sel(rest(a),i-l)

function

sel(a:

string;

integer

{(1

£ 0 and

length (a))});

char;

begin

if/«I

then

sel

first

(a)

D/>1

then

sel«

sel (rest (a),

i -1)

end

Ниже

sel — от

select (выбирать).

—

Прим.

изд. ред.

138 Гл. 2.

Основные

понятия

программирования

Отметим, что в

алголе-68

вместо

sel(a,

i) используется обозна-

чение a[i].

2.3.3.

Рекурсивная

машина

обработки

формуляров

Ход исполнения подпрограммы определён отвечающим ей

формуляром с точностью до

совместности.

Если в самом фор-

муляре снова в качестве операции встречается подпрограмма ',

то необходимо создать формуляр этой подпрограммы

(вызов

подпрограммы,

или

обращение

подпрограмме),

а затем ре-

зультат

её исполнения передать обратно. Это относится и к

рекурсивно определённым подпрограммам — с той лишь осо-

бенностью, что при таких рекурсивных обращениях требуются

новые экземпляры формуляра самой исходной подпрограммы.

При

каждом вызове в новый экземпляр формуляра преж-

де всего заносятся слева соответствующие значения аргументов-

(call

by value

). Каждый такой формуляр называют

воплоще-

нием

подпрограммы; для обозримости можно в

ходе

вычисления

нумеровать все воплощения и соответствующие вызовы.

случае

рекурсии особенно важно, чтобы в

результате

разбора случаев реализовался выбор, который сокращает ра-

боту;

после того как обозначения параметров заменены значе-

ниями,

проставленными слева на формуляре, как можно рань-

ше вычисляются и в основном формуляре, и во

всех

его после-

дующих

воплощениях значения условий и затем исключаются

недопустимые ветви. Рекурсия заканчивается на воплощениях,

которых нет больше ветвей, содержащих рекурсивные вызо-

вы.

Процесс вычисления

завершается

(для заданного набора

значений

параметров), если он

требует

лишь конечного числа

воплощений.

Деятельность человека, который работает с формулярами

указанным образом, может быть очевидным путём механизиро-

вана. Так мы приходим к понятию (мысленной) рекурсивной

машины

—

машины

обработки

формуляров,

в которой по-

прежнему сохраняется полная свобода вычислений. Отметим,

что новый экземпляр формуляра создаётся и

тогда,

когда те же

самые значения уже ранее встречались,— машина обработки

формуляров не учитывает (на описанном здесь уровне) воз-

можность многократного использования однажды полученного

результата.

В частности, упомянутое выше исключение недопустимых

ветвей заведомо возможно, если в условиях нет рекурсивных

Для базовых операций, т. е. для элементарных операций рассматра-

ваемых вычислительных структур, никакого формуляра не требуется.

Вызов значением (англ.). —

Прим.

изд. ред.

2.3. Подпрограммы 139

вызовов. Ещё наглядней случай

линейной

рекурсии,

при кото-

рой,

кроме того, в отдельных ветвях разбора случаев рекурсив-

ный

вызов встречается не более одного раза;

тогда

при

каждом воплощении порождается не более одного нового

воплощения.

Впрочем, почти все ранее изложенные примеры

попадают в этот класс.

Для подпрограммы fac из 2.3.2 машина обработки формуля-

ров работает, как показано на рис. 72. Типичным для рекурсии

•является „задерживание" вычислений, откладывание их „на

потом",—

лишь когда на воплощении

fac

(i)

заканчивается ре-

курсия,

становятся выполнимыми и выполняются вычисления,

отложенные на потом ' в /ас

(2)

fac

fac^

;

окончательный ре-

зультат

поставляет основной формуляр /ас

<0)

. В частном слу-

чае выполнение отложенных операций может свестись к про-

стой передаче результатов отдельных воплощений, как это по-

казано

на рис. 73 для примера вызова

gcdl

(15, 9), см.

2.3.2.

Такие

вызовы называются

гладкими

(или

регулярными).

Если

линейной рекурсии имеются только гладкие вызовы, то гово-

рят о

повторительной

рекурсии.

В линейно-рекурсивных программах — если отвлечься от уже

упоминавшейся совместности для формуляра — порядок, в кото-

ром порождаются требуемые воплощения, определён однозначно.

В общем

случае

это не всегда так: если в какой-то ветви имеется

несколько

вызовов, то при определённых условиях возможны

различные порядки порождения и

даже

параллельная ра-

бота.

Это отражено на рис. 74 для примера программы

sort

из

2.3.2,

в предположении что выполняется двоичная сортировка.

Здесь для последовательности знаков длины 2" получается ров-

но

— 1 воплощений, но всего лишь п + 1 тактов, при

линейной

же сортировке требуется 2" воплощений, но зато 2" так-

тов. Также и в отношении расхода времени на сравнение зна-

ков,

которое необходимо проводить при исполнении подпро-

граммы

merge,

двоичная сортировка выгодней: она

требует

мак-

симум (п—1)Х2+ 1 сравнений, в то время как линейная

сортировка — до 2"-

Х(2" — 1) сравнений.

Во

всех

предыдущих примерах молчаливо принималось оче-

видное правило: начинать новое воплощение, а значит и созда-

вать новый формуляр только

тогда,

когда все аргументы под-

готовлены. Это всегда

будет

предполагаться и в дальнейшем,

т. е. мы принимаем следующий принцип:

Определённая

посредством

описания

подпрограммы

опера-

ция

всегда

рассматривается

как

строгая.

На рис. 59 ромбики, отвечающие задержанным операциям, заштрихо-

ваны.

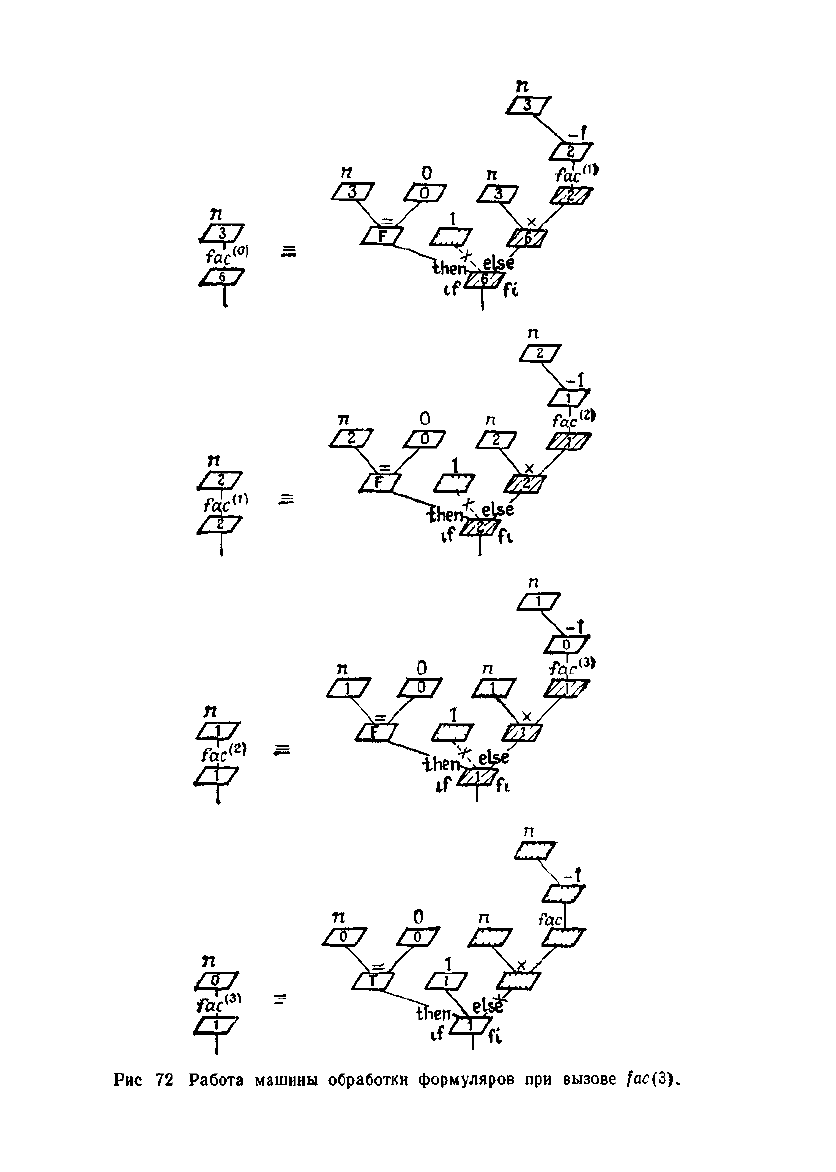
Рис

72 Работа машины обработки формуляров при вызове fac(3).