Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

15.1 Stationary ﬂuid solutions 511

Incidently, we could have found equation (15.25) directly by evaluating equation (15.8)

in a corotating frame. In the corotating frame the velocity must vanish; that means that the

continuity equation (15.6) is satisﬁed identically if ∂

= 0 in that frame. The left hand

side of (15.8) also vanishes with ∂

= 0. Since the corotating frame is not inertial, we

have to include a ﬁctitious centrifugal force in the Euler equation (15.8). We can account

for this term by replacing the Newtonian potential 

with the effective potential



eff

= 

−



. (15.26)

Substituting this relation into equation (15.8) yields equation (15.25) as before.

In summary, we can construct Newtonian models of corotational binaries by solving the

(algebraic) integrated Euler equation (15.25) for the enthalpy h together with Poisson’s

equation (15.5) for the Newtonian potential 

. In these equations the orbital angular

velocity  and the constant of integration C appear as eigenvalues that must be determined

along with solving the equations. We will provide an example of how this can be done

with the help of an iterative algorithm in Section 15.2 below.

Irrotational binaries

For irrotational binaries the curl of the velocity ﬁeld v

has to vanish,



ijk

= 0. (15.27)

We can enforce this by choosing v

to be the gradient of a velocity potential ,

= D

 (irrotational ﬂow). (15.28)

The Euler equations (15.19) now become

−

D

) + D

) =−D

h − D



, (15.29)

which we can again integrate once to ﬁnd the integrated Euler equation

−

D

 + V

 + h + 

= C, (15.30)

where C is again a contant of integration. We now eliminate V

with the help of equa-

tion (15.16)toﬁnd

D

 − k

 + h

Newt

+ 

= C

Newt

. (15.31)

For a given velocity ﬁeld, expressed in terms of , we can intepret this result as an algebraic

equation for the enthalpy h, as we did before for corotating ﬂow.

In contrast to the corotating case, the continuity equation (15.20) is not satisﬁed identi-

cally for irrotational ﬂow. Substituting equation (15.28) we ﬁnd that equation (15.20)now

512 Chapter 15 Binary neutron star initial data

becomes an elliptic equation for the velocity potential ,

 =



− D





ln ρ

. (15.32)

Since the ﬂuid velocity is only deﬁned in the stellar interior, this equation holds in the

stellar interior only, and we need to supply a boundary condition on the stellar surface. At

the surface the density vanishes, so regularity of the right-hand side of equation (15.32)

demands that



− D







surface

= 0. (15.33)

Since D

is normal to the surface, this relation represents a Neumann boundary condition

for .

Exercise 15.2 Show that the boundary condition (15.33) can also be derived from

demanding that, in the corotating frame, the ﬂuid velocity must be tangent to the

stellar surface.

One challenging conceptional issue is already evident: we need to solve equation (15.32)

subject to the boundary condition (15.33), but a priori we don’t know where the stellar

surface, and hence the boundary, is located. One common approach to solving this problem

is to introduce “surface-ﬁtting” coordinates, in which the stellar surface always corresponds

to a ﬁxed coordinate surface.

In summary, then, we can construct Newtonian models of irrotational binary neutron

stars by solving the integrated Euler equation (15.31) for the enthalpy h, the continuity

equation (15.32), subject to the boundary conditions (15.33), for the velocity potential ,

and Poisson’s equation (15.5) for the Newtonian potential 

. As in the corotational case,

the orbital angular velocity  and the constant of integration C appear as eigenvalues, and

have to be solved for together with the equations.

15.1.2 Relativistic equations of stationary equilibrium

We now follow a very similar approach to derive the corresponding equations for relativis-

tic ﬂuids, starting with the conservation of energy-momentum (15.1) and the continuity

equation (15.2). We ﬁrst note that we can rewrite (15.1)as

∇

(hu

) +∇

h = 0. (15.34)

for isentropic conﬁgurations (see equation 5.63). This result is now the relativistic equiv-

alent of the Newtonian Euler equations (15.8).

As in the Newtonian case we proceed by expressing the derivative operators in equa-

tions (15.2) and (15.34) in terms of a Lie derivative along ξ

hel

. Towards that end, we write

See Ury

u and Eriguchi (1999) for a numerical implemention.

15.1 Stationary ﬂuid solutions 513

the ﬂuid 4-velocity u

= u

(ξ

hel

+ V

). (15.35)

Here we assume that ξ

hel

is timelike inside the stars, and we normalize ξ

hel

so that its time

component is unity, ξ

hel

= 1. We also choose V

to be purely spatial, n

= 0, so that it

plays a role that is very similar to that of its Newtonian counterpart in equation (15.16).

In a coordinate system that is comoving with ξ

hel

, i.e., a corotating coordinate system, the

spatial components of the ﬂuid velocity reduce to u

. For a corotating ﬂuid we again

have V

= 0. For convenience of notation we will also deﬁne the spatial projection of hu

= γ

. (15.36)

We now ask the reader to prove two useful identities in exercise 15.3.

Exercise 15.3 Derive the two relations

hel

∇

(hu

) = γ

hel

(hu

) + hD





− hu

(15.37)

and

∇

(hu

) = V

+ hu

. (15.38)

Hint: Choose a coordinate basis as in Chapter 2.7 so that n

= 0 and use equa-

tion (2.62).

We can now relate the spatial projection of the covariant derivative along u

in equa-

tion (15.34) to the Lie derivative along ξ

hel

and spatial derivatives by adding equa-

tions (15.37) and (15.38),

∇

(hu

) = u



hel

∇

(hu

) + γ

∇

(hu

)



= u



hel

(hu

) + hD





+ V



. (15.39)

Combining this result with equation (15.34)weﬁnd

hel

(hu

) + D





+ V

− D

) = 0. (15.40)

With the help of equation (2.63) we can also express equation (15.2)as



hel

(ρ

) + ρ

∇

hel



+ D

(αu

) = 0. (15.41)

Since we have not yet used the fact that ξ

hel

is a Killing vector, equations (15.40)and

(15.41) are still completely general. As in the Newtonian derivation we can now specialize

In this section we follow the notation and approach of Shibata (1998).

514 Chapter 15 Binary neutron star initial data

to equilibrium conﬁgurations by invoking that ξ

hel

be a helical Killing vector.

In this

case the Lie derivatives along ξ

hel

, as well as the divergence ∇

hel

, must vanish, so that

equations (15.40) and (15.41)reduceto





+ V

− D

) = 0 (15.42)

and

(αu

) = 0. (15.43)

Exercise 15.4 Show that in the Newtonian limit equations (15.42)and(15.43)

reduce to the Newtonian equations (15.19)and(15.20).

Hint: Use exercise 2.28 and equation (5.22) to ﬁnd the Newtonian limits of α and

αu

As in the Newtonian case, equations (15.42) and (15.43) simplify further for either

corotational or irrotational ﬂuid ﬂow. We will discuss these two cases separately in the

following two sections.

15.2 Corotational binaries

We can construct corotational binaries by requiring that the ﬂuid ﬂow vanish in the frame

corotating with the binary,

= 0. (15.44)

With this choice, the continuity equation (15.43) is satisﬁed identically, as in our Newtonian

analysis, and the Euler equations (15.42) reduce to





= 0. (15.45)

We can again integrate these equations immediately to obtain the integrated Euler equation

= C, (15.46)

where C is a constant of integration. In fact, this result proves relation (5.58).

From the normalization u

=−1wealsohave

αu



1 + γ



1/2

(15.47)

Recall that for relativistic binaries, we seek a quasiequilibrium state, for which ξ

hel

is really only an approximate Killing

vector; see the discussion leading up to equation (12.63).

In some of the literature this expression is incorrectly refered to as the Bernoulli equation; compare equations (5.57)

and (5.58) and the related discussion in Chapter 5.

15.2 Corotational binaries 515

(see equation 5.11). In a typical application, the spatial metric will be rescaled conformally,

= ψ

¯γ

. Given a choice for the conformal background metric ¯γ

, and given values

for the lapse α, the conformal factor ψ, and the shift β

, we can use equations (15.35)and

(15.11) (adopting the form 15.13 when working in Cartesian coordinates) to obtain u

Substituting this result into equation (15.46) yields an algebraic expression for h.

Exercise 15.5 Show that, for a conformally ﬂat spatial metric, the enthalpy h

satisﬁes

− ψ



(y − β

)

+ (x +β

)

+ (β

)

,

1/2

= C (15.48)

if the axis of rotation is aligned with the z-axis. Verify that this expression reduces

to equation (15.25) in the Newtonian limit.

Hint: Use exercise 2.28.

In typical applications equation (15.48) – or an equivalent equation if the background is

not conformally ﬂat – is solved in conjunction with the conformal thin-sandwich equations

(3.109)–(3.112) listed in Box 3.3. The latter provide a set of equations for the conformal

factor ψ, the lapse α, and the shift β

in terms of matter sources that depend on h.

Furthermore, we can use equation (15.48) to compute h algebraically in terms of ψ, α,

and β

. As before, the constants  and C appear as eigenvalues in this equation, and have

to be determined in the course of solving for the ﬁeld and matter variables.

It is worth noting why it is the conformal thin-sandwich formalism of Chapter 3.3,

rather than the conformal transverse-traceless approach of Chapter 3.2, that is relevant in

this context. A quick glance at equation (15.48)revealsthatwerequirealapseα and a

shift β

to solve the quasiequilibrium problem. The conformal thin-sandwich formalism

provides these functions, while the conformal transverse-traceless formalism does not.

More fundamentally, we wish to construct ﬂuid conﬁgurations that are in quasiequilibrium,

so that Lie derivatives along a timelike Killing vector vanish. To impose this condition, we

need to constrain the behavior of the spacetime in a neighborhood of a spatial slice  and

not merely on . The conformal thin-sandwich formalism is an approach that allows us to

impose quasiequilibrium in just this fashion.

A number of different numerical algorithms have been implemented to construct simul-

taneous solutions to the integrated Euler equation (15.48) and the ﬁeld equations (3.109)–

(3.112).

We will describe one such scheme, namely that of Baumgarte et al. (1997, 1998a),

which is based on a similar scheme for constructing rotating stars developed by Hachisu

(1986). We will also focus on the Newtonian problem, which is simpler than the relativistic

case, and yet captures all the key ingredients of the numerical scheme. Instead of the rela-

tivistic integrated Euler equation (15.48) we will therefore solve its Newtonian counterpart

(15.25), and instead of the ﬁeld equations (3.109)–(3.112) we will solve Poisson’s equation

(15.5).

See, e.g., Baumgarte et al. (1998a); Marronetti et al. (1998); Gourgoulhon et al. (2001); Taniguchi and Gourgoulhon

(2002).

516 Chapter 15 Binary neutron star initial data

We start by choosing an equation of state. For simplicity, we adopt a -law equation of

state

P = ( − 1)ρ

 (15.49)

(see equation 5.17). For isentropic ﬂuids, this equation of state is equivalent to a polytropic

equation of state of the form

P = Kρ



,= 1 + 1/n, (15.50)

where n is the polytropic index and K is the gas constant (see exercise 5.5). Choosing

a polytropic equation of state allows for several simpliﬁcations in our scheme, but very

similar algorithms can be used for any other equation of state, even if it exists only in

tabulated form.

The Newtonian enthalpy h

Newt

that appears in equation (15.25) can then be written as

Newt

=  +

= (n + 1)

. (15.51)

If we also assume that the binary rotates about the z-axis, the integrated Euler equation

(15.25) takes the form

(n + 1)

+ 

−



+ y

) = C

Newt

. (15.52)

For polytropes it is convenient to introduce the dimensionless density parameter

q ≡

, (15.53)

in terms of which we have

= K

−n

, P = K

−n

n+1

. (15.54)

Since physical units enter the problem only through the constant K , we can introduce

dimensionless coordinates

x = K

−n/2

x and similar for y and z,asinequation(14.17).

The angular velocity scales as

 = K

n/2

 and the Laplace operator as

= K

.In

terms of these quantities, equation (15.52) becomes

(n + 1) q + 

−



(

) = C

Newt

, (15.55)

and Poisson’s equation becomes



= 4πq

. (15.56)

We simplify the problem further by treating equal-mass binaries. These binaries form a

two-parameter family of solutions that can be parametrized, for example, by the maximum

Here we depart from our previous notation convention: the bar denotes the nondimensional operator, and not the

conformally-related operator as deﬁned elsewhere in the book.

15.2 Corotational binaries 517

density of each star and their separation. Instead of using the absolute separation of the

binary stars, we will specify their relative separation as follows: Assume that the binary lies

along the x-axis, i.e., the x-axis connects the points of maximum density in the two stars.

Let x = 0 reside at the center of mass, midway between the stars. Denote the coordinate

along x at the nearest point to the origin on the surface of one star by x

and at the farthest

point by x

. Also label the point of maximum matter density in the star by x

. We can then

parametrize the binary separation in terms of the relative separation s = x

An inﬁnite separation corresponds to s = 1, while a contact binary has a separation

s = 0.

In fact, it proves convenient to rescale not only

with respect to

(to deﬁne the

relative separation s), but all coordinates as well. Denoting these rescaled coordinates with

a caret, we deﬁne

x =

and similarly for

y and

z. The Laplace operator now rescales

, and we also have

 =

. Poisson’s equation now takes on the form



= 4π

. (15.57)

Equation (15.57) motivates the scaling relation



(15.58)

for the Newtonian potential, whereby equation (15.57) reduces to



= 4πq

. (15.59)

The integrated Euler equation (15.55) then takes the form

(n + 1) q +



−



(

) = C

Newt

. (15.60)

We now have to ﬁnd simultaneous solutions to equations (15.59) and (15.60)forq and



together with the eigenvalues

, C

Newt

and

. This can be accomplished by the following

iteration scheme:

Choose the polytropic index, then select a particular binary model by specifying the

maximum density, q

max

, and the relative binary separation s.

1. As a ﬁrst step in the iteration, provide an initial guess for the density proﬁle q.For

example, this can be a spherical density proﬁle with maximum density q

max

and properly

rescaled so that it is conﬁned between

and

2. Next, solve Poisson’s equation (15.59), which requires solving an elliptic equation. This

can be accomplished, for example, by employing the algorithms described in Chapter

6.2.2 for ﬁnite difference methods, or in Chapter 6.3.4 for spectral methods. Solving

equation (15.59) provides the rescaled Newtonian potential



This parametrization is not unlike that for a family of isolated, uniformly rotating stars, members of which can be

parametrized by their maximum density and the ratio between their polar and equatorial radii. It is therefore possible

to construct binary neutron stars with an iterative algorithm similar to one used for isolated rotating stars; see Chapter

14.1.2.

518 Chapter 15 Binary neutron star initial data

3. Then, determine the eigenvalues

, C

Newt

and

by evaluating the integrated Euler

equation (15.60) at the three points

= s,

= 1and

.Toﬁnd

, locate the (cur-

rent) point of maximum density along the x-axis. At all of these three points we know

the value of q:at

and

we must have q = 0, since both points lie on the stellar

surface, and at

we must have q = q

max

. Evaluating (15.60) at these three points

yields the three equations



−



= C

Newt



−



= C

Newt

(n + 1) q

max



−



= C

Newt

(15.61)

This set of equations can be solved iteratively for the eigenvalues

, C

Newt

and

4. With the values of the eigenvalues

, C

Newt

and

ﬁnd the new density distribution q

by solving equation (15.60) in the stellar interior.

5. Given the new density distribution q, now evaluate the residual of Poisson’s equation

(15.59). If this residual is larger than some predetermined tolerance, then the iteration

continues, beginning with step 2 above. Otherwise the solution has been obtained to

within the desired accurcay, and the iteration terminates.

The above iterative scheme describes the method to solve the Newtonian problem, but

a very similar algorithm can be used to solve the corresponding relativistic problem. The

equations are more complicated, of course, and instead of solving one equation for the

Newtonian potential we now have to solve the ﬁve equations (3.109)–(3.112)forα, ψ

and β

, but all of these changes can be accommodated by the above iteration scheme. One

complication arises from the scaling of the gravitational ﬁelds, which are less obvious in

the relativistic case. However, for the purposes of this iteration, we can rescale α and ψ in

such a way that in the Newtonian limit we recover the scaling relation (15.58).

Solving the above equations then allows us to construct relativistic, quasiequilibrium

binary neutron star models. Figure 15.1 shows a typical neutron star binary at a small sepa-

ration. Subjected to a small tidal distortion, the proﬁle of each star assumes a characteristic

prolate shape.

As a ﬁrst application, we can now generalize Oppenheimer–Volkoff sequences (see

Chapter 1.3). In an Oppenheimer–Volkoff sequence we ﬁx the equation of state and

construct spherically symmetric, static neutron stars with different central densities. Along

such a sequence, the conﬁguration with the maximum total mass-energy M(= M

ADM

)is

also the conﬁguration with the maximum rest-mass M

and locates the maximum central

density beyond which stars in isolation are radially unstable. Generalizing such sequences

to binaries, we can ﬁx the separation s and construct sequences of binaries with identical

15.2 Corotational binaries 519

Figure 15.1 Rest-mass density contours in the equatorial plane for a neutron star binary orbiting close to the

ISCO. These stars satisfy a polytropic equation of state with n = 1, and each star has a rest mass of

= 0.169,

corresponding to a compaction in isolation of (M/R)

∞

= 0.175. (The maximum-mass conﬁguration in isolation

has

= 0.180 and (M/R)

∞

= 0.215.) The lines correspond to contours of constant rest-mass density in

decreasing factors of 0.556. [From Baumgarte et al. (1998a).]

companions, parametrized by the maximum density inside each star.

Clearly, for inﬁnite

separation (s = 1) this sequence should reduce to an Oppenheimer–Volkoff sequence for

each companion, at least up to numerical error.

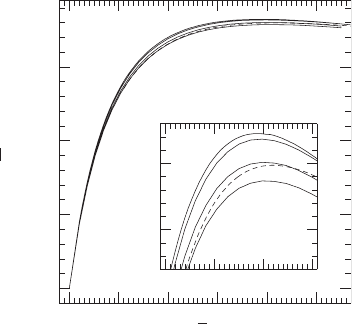
In Figure 15.2 we show some results for n = 1 polytropic binaries constructed by ﬁnite

differencing on a very coarse, 3-dimensional grid. These particular models were computed

on a uniform grid of (64)

grid points, with the outer boundary placed at such a distance

that the stellar interior along the x-axis is always covered by 17 grid points. The dashed

line represents the Oppenheimer–Volkoff sequence, while the solid lines represent binaries

of successively decreasing binary separation s, moving from the bottom to top curve. The

ﬁnite difference error in the binary calculations systematically underestimates the mass,

which explains why these curves do not converge to the Oppenheimer–Volkoff result as

one would expect. We nevertheless notice that the curves for smaller binary separations lie

above those for larger binary separation in the graph. This result implies that the maximum

allowed mass increases with decreasing binary separation and reﬂects the fact that tidal

forces serve to stabilize neutron stars against radial instability.

Figure 15.2 also has an important consequence for evolutionary sequences. For sufﬁ-

ciently large binary separations, at which the binary evolves very slowly, we can construct

We allow for the possibility that the maximum density does not reside at the coordinate “center” of the star.

Recall that Oppenheimer–Volkoff solutions satisfy ordinary differential equations, which can be solved to essentially

arbitrary precision.

See Baumgarte et al. (1998b) for a stability analysis of corotating, relativistic binary stars.

520 Chapter 15 Binary neutron star initial data

0 0.1 0.2

0.2

0.175

0.18

0.3

0.4

0.5

0.15

0.1

0.05

Figure 15.2 Rest mass

vs. central density ¯ρ

∗

along sequences of equal-mass, corotational binary

companions obeying an n = 1 polytropic EOS. Successive curves are for binary separations ranging from

s = 0.3 (bottom solid line), through 0.2 and 0.1, and extending to 0.0 (top line). The dashed line is the

Oppenheimer–Volkoff limiting curve for isolated static stars (s = 1). Due to ﬁnite difference errors, the numerical

values systematically underestimate the mass, hence some of the curves creep below the Oppenheimer–Volkoff

curve. The insert is a blow-up of the region around the maximum masses. [From Baumgarte et al. (1997).]

a quasiequilibrium inspiral sequence by “gluing” together quasiequilibrium models at

different binary separations. For binary neutron stars the rest mass M

(e.g., the baryon

number) must be constant along such an evolutionary sequence.

In Figure 15.2, such an

evolutionary sequence must start at very large separation with conﬁgurations lying close

to some point on the stable branch of the Oppenheimer–Volkoff sequence. As the binary

emits gravitational radiation, loses energy and angular momentum and spirals inward, it

must evolve along a horizontal line of constant rest mass M

in Figure 15.2. This implies

that the maximum density decreases as the binary separation decreases and the stars are

tidally elongated.

Whether the maximum density in binary neutron stars increases or decreases with

decreasing binary separation was once the subject of an interesting controversy.

Origi-

nally, a “star-crushing” effect was reported by Wilson and Mathews (1995),

whereby the

maximum density in binary neutron stars increases as the two stars approach each other,

ultimately triggering a radial instability and a “binary-induced” collapse to two individual

black holes prior to binary merger. This effect runs counter to Newtonian intuition and

calculations, which argue that a tidal elongation in a quasiequilibrium ﬂuid binary star

Compare the discussion in Chapter 12.4 for binary black holes.

See Kenneﬁck (2000) for an account of the sociological aspects of this controversy.