Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

15.2 Corotational binaries 521

−0.05

−0.15

2 2.5 3

3.5

−0.1

∆ r

max

∞

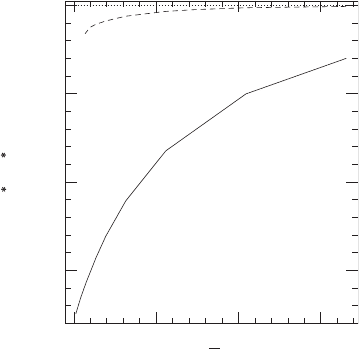
Figure 15.3 The relative change in the maximum density ρ

∗

max

/ρ

∗∞

max

as a function of the separation

d between

the locations of the maximum densities in an equal-mass, n = 1 polytropic binary with companions of rest-mass

= 0.18 (close to the maximum allowed mass for static stars). The solid line marks the changes in the density

for corotational binaries, and the dashed line for irrotational binaries. The dotted lines marks ρ

∗

max

= 0. This

graph shows that the central density decreases with decreasing binaries for both corotational and irrotational

binaries. Similar results hold for binaries of different masses and polytropic indices, and also for unequal-mass

binaries. [After Taniguchi and Gourgoulhon (2002).]

should reduce the density inside a star.

As a consequence, the “star-crushing” effect was

met with great skepticism in the community.

Our argument above, based on Figure 15.2, also suggests that the central density should

decrease, and not increase, with decreasing binary separation. However, this argument

only holds for corotational binaries. At small binary separations corotational binaries have

to spin very fast to keep up with the orbit. This spin by itself leads to a ﬂattening of

the star and hence may lead to a reduction in the central density, even in isolated stars.

Moreover, corotation is not maintained during binary inspiral for realistic neutron stars,

as we discussed in Section 15.1. The more relevant question is therefore how the central

density behaves in irrotational binaries. Anticipating ﬁndings from Section 15.3 we show

in Figure 15.3 results for irrotational quasiequilibrium binaries, as well as more accurate

results for corotational, binaries. This plot demonstrates that, while the effect is indeed

much smaller for irrotational binaries than for corotational binaries, the central density

decreases with decreasing binary separation in both cases.

Ultimately, the original controversy was resolved when a mistake was found in the cal-

culations of Wilson and Mathews (1995)andWilson et al. (1996)(seeFlanagan 1999).

Correcting this mistake reduced the size of the reported effect dramatically.

More signif-

icantly, no sign of a “crushing instability” has been observed in any other post-Newtonian

See Rasio and Shapiro (1999) for a review and references.

Mathews and Wilson (2000).

522 Chapter 15 Binary neutron star initial data

0 0.01 0.02

Ω

1.5

[Hz]

0.2

0.03 0.04

0.05

200 400

n = 1.0

(M −M

∞

) /M

600 800

0.04

0.03

0.02

0.01

−0.005

−0.01

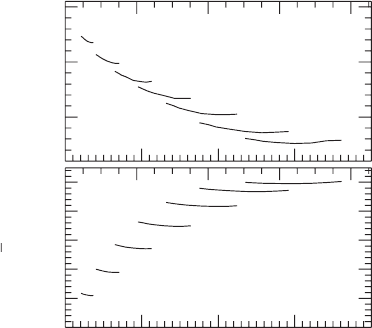
Figure 15.4 The binding energy and angular momentum as functions of orbital angular velocity for several

different values of the rest mass

. The curves are labeled by the compaction (M/R)

∞

that the stars would have

at inﬁnite binary separation, starting with 0.05 and increasing in steps of 0.0025 up to 0.2. The maximum

compaction of a stable, isolated, nonrotating n = 1 polytrope is 0.217. The upper label gives the orbital frequency

for stars with a rest mass of 1.5M



.[FromBaumgarte et al. (1998a).]

or fully relativistic simulation of neutron star inspiral and merger

as we will discuss in

Chapter 16, although no theorem has been proven to completely rule out the possibility.

As we discussed in Chapter 12.1, the innermost stable circular orbit (ISCO) marks a

transition from a slow, quasistationary inspiral to a rapid plunge and merger. While this

transition may not be particularly abrupt, crossing the the ISCO will mark a transition in

the emitted gravitational waveform away from a quasiperiodic chirp signal (see Chapter

16). Locating the ISCO and the orbital frequency to which it corresponds are therefore

important goals when constructing quasiequilibrium sequences of binary neutron stars.

We can identify the ISCO by locating the minimum of the total ADM energy M

ADM

along an evolutionary sequence of constant rest-mass M

(see Chapter 12.1). As discussed

in Chapter 12 in conjunction with equation (12.112),

ADM

= dJ, (15.62)

a minimum in the energy should coincide with a minimum in the angular momentum. In

Figure 15.4 we show some numerical results obtained on a coarse grid for the fractional

binding energy (M

ADM

− M

∞

ADM

)/M

and the angular momentum

J for sequences of

Such an effect can occur in binaries consisting of collisionless clusters; Shapiro (1998); Duez et al. (1999).

See, e.g., Favata (2006).

15.3 Irrotational binaries 523

Table 15.1 The orbital angular velocity , angular momentum J and ADM mass

ISCO

at the

ISCO, for corotating, equal mass, binary neutron stars with polytropic index n = 1. We tabulate

the rest-mass

, the ADM mass

∞

and the compaction (M/R)

∞

each star would have in

isolation (where R is the areal radius), as well as the angular velocity M

, angular momentum

tot

(where “tot” means total ADM value) and ADM mass

ISCO

≡ M

tot

/2attheISCO.

For this EOS the maximum rest mass in isolation is

max

= 0.180. [After Taniguchi and

Gourgoulhon (2002).]

∞

(M/R)

∞



ISCO

tot

)

ISCO

0.130 0.122 0.12 0.0139 1.136 0.1213

0.146 0.136 0.14 0.0175 1.075 0.1350

0.160 0.148 0.16 0.0217 1.028 0.1464

0.171 0.157 0.18 0.0253 0.994 0.1550

constant rest mass

. In the deﬁnition of the binding energy, M

∞

ADM

denotes the ADM

mass that this star would have at inﬁnite binary separation. We plot these quantities vs.

the orbital frequency instead of binary separation, because the former is a gauge-invariant

quantity while the latter is not.

Figure 15.4 suggests that the minima in the binding energy

(and hence the ADM mass) do indeed coincide with those of the angular momentum, and

thereby identify the ISCO.

In Table 15.1 we list the angular velocity M

, the total angular momentum J

tot

(where M

tot

is the total ADM mass of the binary system), and the individual ADM mass

ISCO

≡ M

tot

/2 at the ISCO for different values of the stellar rest mass M

for equal-

mass, n = 1 polytropes. As it turns out, only stars with sufﬁciently stiff equations of state

∼

1.0) encounter an ISCO before they touch, which is in qualitative agreement with

Newtonian results.

Stars with softer equations of state are more centrally condensed and

have more extended envelopes, so that they come into contact and merge before reaching

an ISCO.

As we discussed in Section 15.1 above, the assumption of corotation is very unrealistic,

since it requires an unrealistically large viscosity. To obtain results that are of greater

astrophysical relevance than those found in this section, we must consider irrotational

binaries.

15.3 Irrotational binaries

We can ﬁnd a set of equations that governs irrotational binaries in close analogy to our

Newtonian treatment in Section 15.1.1.

In general relativity, the vorticity tensor ω

can

Also, the observed gravitational wave spectrum is dominated by mass quadrupole emission at frequency f

= /π.

See, e.g., Rasio and Shapiro (1999) for a review and references.

The ﬁrst relativistic formalism for irrotational binaries in quasiequilibrium was presented in Bonazzola et al. (1997).

Subsequently, other approaches were developed by Asada (1998), Teukolsky (1998)andShibata (1998). Gourgoulhon

(1998) demonstrated that all of these formulations are equivalent. The derivation here follows that of Shibata (1998).

524 Chapter 15 Binary neutron star initial data

be deﬁned as

≡ P

(

∇

(hu

) −∇

(hu

)

, (15.63)

where P

= g

+ u

is the projection operator with respect to the ﬂuids’s 4-velocity

(equation 5.67). For irrotational binaries the vorticity must vanish,

= 0, (15.64)

which is equivalent to the Newtonian condition (15.27). For this to be the case, the quantity

must be the gradient of a velocity (scalar) potential ,

=∇

; (15.65)

cf. (15.28).

Exercise 15.6 Show that with equation (15.65) the continuity equation (15.2)

reduces to

∇



∇





= 0, (15.66)

while the Euler equation (15.34) is satisﬁed identically.

Exercise 15.7 (a) Use the Euler equation (15.34) to show that ω

can be written

=∇

(hu

) −∇

(hu

). (15.67)

(b) Evaluate equation (5.59) to show that for irrotational ﬂow in an isentropic ﬂuid

the circulation satisﬁes

C = 0.

With the deﬁnition (15.36), the spatial projection of equation (15.65) becomes

= D

. (15.68)

In the Euler equation (15.42) this result now eliminates the second term, so that we can

integrate the ﬁrst term once to ﬁnd

= C, (15.69)

where C is again a constant of integration.

It is now convenient to introduce a rotational shift vector

= β

+ k

, (15.70)

where k

is given by equation (15.11)ask

= ξ

hel

− t

. From equation (2.98)wehave

= αn

+ β

, so that we can write B

= ξ

hel

− αn

. (15.71)

We now solve equation (15.35)forV

, substitute equation (15.71)forξ

hel

, take the spatial

projection (to eliminate the αn

term), substitute equation (15.68)foru

, and obtain

15.3 Irrotational binaries 525

ﬁnally

 − B

. (15.72)

As we did for corotational binaries, we now use the normalization u

=−1 to express

in terms of the spatial components of the 4-velocity. Substituting equation (15.68) into

(15.47) yields

αu



1 + h

−2

D





1/2

. (15.73)

We next combine equations (15.69), (15.72) and (15.73)toﬁnd

αu

αh



C + B





. (15.74)

We digress to note an interesting result derived in exercise 15.8.

Exercise 15.8 Use L

hel

(hu

) = 0 to show that

hel

 = ξ

∇

 =−C



(15.75)

where C



is a constant.

Naively, we might have expected that the Lie derivative of  along the Killing vector

hel

vanishes. However,  is only a potential and not a measurable (physical) quantity. Only

the gradient of , ∇

 = hu

, is measurable, and therefore only for the gradient can we

impose the Lie derivative along ξ

hel

to vanish.

As we have found in exercise 15.8, this

introduces a constant of integration when we evaluate the Lie derivative of  itself. We

can now use the result (15.75) to provide an alternative derivation of equation (15.74)(see

exercise 15.9).

Exercise 15.9 Replace n

in hαu

=−hn

=−n

∇

 with the help of equa-

tion (15.71) to rederive equation (15.74).

We can ﬁnally combine equations (15.73) and (15.74)toﬁnd

(C + B

)

− D

D

. (15.76)

As in the Newtonian derivation, the integrated Euler equation (15.69) furnishes an algebraic

expression for the enthalpy h. We could have left this equation in the form (15.69), but

since h also appears in V

we have taken a few more steps to isolate h in equation (15.76).

We still need an equation for the velocity potential , which we can ﬁnd from the

continuity equation (15.43). Inserting (15.72)into(15.43) we obtain

(αρ

−1

) − D

(αu

) = 0. (15.77)

See also Teukolsky (1998), who shows formally that L

hel

= 0 = L

hel



d =



hel

 (see exercise A.3), which

implies equation (15.75).

526 Chapter 15 Binary neutron star initial data

To eliminate u

we can now insert equation (15.74) and ﬁnd, just like in the Newtonian

case, an elliptic equation for the velocity potential ,

 − D



C + B







C + B



− D





αρ

(15.78)

Equations (15.76) and (15.78) now provide two equations for the two ﬂuid variables h

and . Equation (15.78) is an elliptic equation and hence needs to be supplemented

with boundary conditions for  on the stellar surface. Since ρ

vanishes there, regularity

requires



C + B



− D







surface

= 0. (15.79)

This is again a Neumann boundary condition. Just like its Newtonian equivalent (15.33)

this condition enforces the ﬂuid ﬂow to be tangent to the surface.

Exercise 15.10 Show that in the Newtonian limit equations (15.76), (15.78)and

(15.79) reduce to the Newtonian equations (15.31), (15.32)and(15.33).

In most applications to date, the matter equations (15.76) and (15.78) have been solved

together with the conformal thin-sandwich equations (3.109)–(3.112)forthelapseα,the

shift β

and the conformal factor ψ. Constructing irrotational binaries is much more

involved than constructing corotational binaries. By contrast with corotational binaries,

where only one algebraic equation (15.46) has to be solved for the enthalpy, we now have

to solve the enthalpy equation (15.76) together with the elliptic equation (15.78) for the

velocity potential , subject to the boundary condition (15.79) on the surface of the star.

The latter adds another complication, since the location of the surface is not known a priori.

Bonazzola et al. (1999a)andGourgoulhon et al. (2001) solved this problem with the

help of a multidomain, spectral method that covers the entire computational domain with

several patches of coordinate systems. In particular, the interiors of the stars are covered

with spherical-type coordinate systems, which are constructed so that the surface of the

star lies at a constant value of the radial coordinate. Such coordinate systems are called

“surface-ﬁtting” coordinates, and are very well suited for imposing the boundary condition

(15.79). A similar algorithm, based on Newtonian simulations of irrotational neutron star

binaries,

has been used by Ury

u et al. (2000).

As a brief, technical detour, we point out why it is natural for these calculations in

spherical polar coordinate systems to use two computational domains, each one centered

on one of the binary companions. Consider an equation of the form

φ = RHS, (15.80)

Ury

u and Eriguchi (1999).

See also Ury

u and Eriguchi (2000).

15.3 Irrotational binaries 527

x [km]

y [km]

4020−20−40

−50

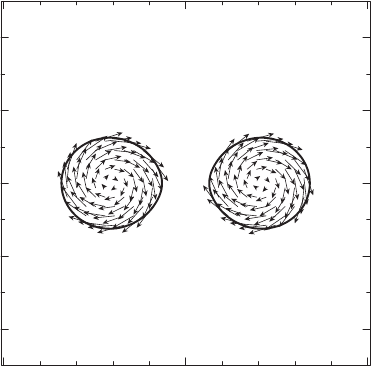
Figure 15.5 The internal velocity ﬁeld with respect to the corotating frame in the orbital plane for identical stars

of rest mass M

= 1.625M



at a coordinate separation of 41 km. The binary stars are irrotational and

constructed from an n = 1 polytropic EOS with K = 1.8 ×10

−2

/kg

. The thick lines mark the stellar

surfaces. [From Gourgoulhon et al. (2001).]

where RHS symbolizes some potentially nonlinear source terms on the right hand side.

We can choose to solve this equation by splitting it into the two equations

= RHS

(15.81)

where φ = φ

+ φ

and RHS = RHS

+ RHS

, and where each equation is now associated

with one of the two stars. The two equations in (15.81) can then be solved on two separate

computational domains, each one centered on one star. Clearly, the separation of the source

terms RHS into the two parts RHS

and RHS

is far from unique. One guiding principle

is to move those parts of RHS that are large in the neighborhood of star 1 into RHS

and similarly for the other star. Another principle is that each of the source terms should

asymptotically coincide with those for the corresponding isolated star when the binary

separation is large.

We show a typical binary conﬁguration and its internal velocity ﬁeld in Figure 15.5.As

we did for corotational binaries, we can determine the maximum allowed mass of neutron

stars in irrotational binaries by ﬁrst ﬁnding the mass as a function of central density for

ﬁxed separation, and then varying the separation. In Figure 15.6 we show results of Ury

et al. (2000), which demonstrate that, as in corotational binaries, the maximum mass

increases with decreasing separation. However, by comparing with Figure 15.2, we note

that the increase in maximum mass is smaller for irrotational binaries than for corotational

528 Chapter 15 Binary neutron star initial data

0.25 0.27 0.29 0.31 0.33 0.35

(ρ

max

)

0.177

0.178

0.179

0.18

0.181

0.182

Figure 15.6 The rest mass

as a function of maximum density ¯ρ

for separations

d = 1.3125, 1.375,

1.5, 1.625, 1.75, 1.875 and 2 (thick lines running from top to bottom) of irrotational, binary neutron stars

constructed from an n = 1 polytropic EOS. The dashed line is the Oppenheimer–Volkoff result. [From Ury

et al. (2000).]

binaries.

This result is not surprising, since neutron stars in corotational binaries are

spinning with respect to the inertial frame at rest with respect to the binary center. This

spin by itself increases the maximum mass of neutron stars.

It is also evident from

Figures 15.6 and 15.2 that, while the density along evolutionary sequences of irrotational

binaries of constant rest mass

decreases with decreasing separation, the decrease is

less than that for corotational binaries, which we had already anticipated in Figure 15.3.

As we have seen in Section 15.2, evolutionary sequences of corotational binaries typ-

ically end either at the ISCO or at contact. Irrotational sequences, on the other hand,

typically end when a cusp forms on the stellar surface, prior to reaching the ISCO or

contact.

Such a cusp forms when the stellar surface reaches an inner Lagrange point, so

that matter can start ﬂowing from one star to its companion.

A potential disadvantage of using spectral methods for constructing these binaries is

that the appearance of such a cusp on the stellar surface leads to Gibbs phenomena and

hence decreasing accuracy. Typically, sequences constructed with spectral methods must

therefore terminate shortly before the appearance of a cusp. To identify cusp formation,

many authors

introduce a “mass-shedding indicator” χ, deﬁned as the ratio between the

radial derivative of the speciﬁc enthalpy h on the neutron star equator at the point nearest

to the companion to the radial derivative at the pole,

χ ≡

∂

(ln h)

∂

(ln h)

pole

. (15.82)

This result is especially evident taking into account the coarse resolution used by Baumgarte et al. (1998a), which

underestimate the masses in Figure 15.2.

See, e.g., Cook et al. (1994b) as well as Chapter 14.

Bonazzola et al. (1999a); Ury

u and Eriguchi (2000); Ury

u et al. (2000).

See, e.g., Gourgoulhon et al. (2001).

15.3 Irrotational binaries 529

Table 15.2 The orbital angular velocity , angular momentum J and the ADM mass

M at cusp

formation, for irrotational, equal-mass, binary neutron stars with polytropic index n = 1. We tabulate the

individual rest mass

, the ADM mass

∞

and the compaction (M/R)

∞

each star would have in

isolation (where R is the areal radius), as well as the angular velocity M

, the angular momentum

tot

(where “tot” means total ADM value) and the ADM mass

CUSP

= M

tot

/2 at cusp formation.

For this EOS, the maximum rest mass in isolation is

max

= 0.180. [After Taniguchi and Gourgoulhon

(2002).]

∞

(M/R)

∞



CUSP

tot

)

CUSP

0.130 0.122 0.12 0.0142 0.997 0.1211

0.146 0.136 0.14 0.0181 0.947 0.1347

0.160 0.148 0.16 0.0222 0.910 0.1460

0.171 0.157 0.18 0.0265 0.881 0.1546

This indicator is identically one for a spherical star and falls to zero at the appearance of a

cusp. We can then tabulate χ as a function of binary separation, or orbital angular velocity,

and extrapolate to χ = 0 to identify the onset of cusp formation.

Ury

u et al. (2000) ﬁnd that equal-mass, irrotational binaries reach an ISCO before a cusp

appears only for very stiff equations of state (n

∼

2/3), while binaries with softer equations

of state form a cusp ﬁrst. In Table 15.2 we list some parameters for irrotational, equal-mass

n = 1 binaries at cusp formation. Comparing with the corresponding ISCO parameters

of corotational binaries in Table 15.1, we note that the cusp and ISCO occur at quite

similar frequencies. The corotational binaries have more angular momentum, because the

individual stars carry a spin in addition to the orbital angular momentum of the binary. We

also ﬁnd that the binding energy (

M −

∞

of corotational binaries is slightly larger

than for irrotational binaries. This is because the ADM mass

M of the former include the

additional spin kinetic energies of the individual stars.

For additional numerical results,

including models for different equations of state and unequal-mass binaries, we refer the

reader to the literature.

In all of the above calculations the matter equations (15.76), (15.78) and (15.79)have

been solved together with the conformal thin-sandwich formalism of Chapter 3.3 for the

gravitational ﬁelds, as summarized in Box 3.3. However, it is not clear that this formalism

is the best possible approach for constructing quasiequilibrium binaries. In particular,

this approach makes an ad hoc choice for the conformally-related background metric ¯γ

which may or may not lead to the best approximation of quasiequilibrium. Several authors

have therefore suggested alternative methods that may produce more accurate models of

compact binaries in quasiequilibrium.

See also the discussion in Duez et al. (2002).

See, e.g., Taniguchi and Gourgoulhon (2002, 2003).

See, e.g., Blackburn and Detweiler (1992); Andrade et al. (2004); Shibata et al. (2004); Friedman and Ury

u (2006)

and references therein.

530 Chapter 15 Binary neutron star initial data

One of these alternative approaches is the “waveless” approximation of Shibata et al.

(2004) that we discussed brieﬂy in Chapter 3.4. Ury

u et al. (2006) implemented this

scheme for binary neutron stars. As expected, for stars with small compaction they obtain

results that are very similar to those found with the conformal thin-sandwich approach

assuming conformal ﬂatness. For stars with a larger compaction, however, their results

show some deviation from both the conformally ﬂat models as well as third post-Newtonian

(3PN) point-mass calculations. For stars with a compaction (M/R)

∞

= 0.17, at a binary

separation at which the coordinate distance from the orbital center to the geometric center

of each star is 1.75R

∞

, the conformally related metric, for example, deviates from a ﬂat

metric by about 1%. The deviations in the binding energy are comparable. To establish

whether or not these models are closer to quasiequilibrium than the conformally ﬂat

models presumably requires a fully dynamical hydrodynamic simulation. We describe

such simulations for binary neutron stars in Chapter 16.

15.4 Quasiadiabatic inspiral sequences

In the previous sections we have discussed how we can construct individual models of

binary neutron stars in circular orbit at arbitrary binary separations. We have also mentioned

that we can “stitch” together models of constant rest mass M

to build evolutionary inspiral

sequences. In this section we will describe how such a “quasiadiabatic” approach can be

used to calculate the gravitational wave signal from the late inspiral phase, prior to plunge

and merger.

We start by approximating the binary orbit outside the ISCO as circular, and by treating

the orbital decay as a small correction. For each binary separation we can then ﬁnd the

matter distribution using the quasiequilibrium methods of the previous sections. Next we

need to ﬁnd the gravitational wave signal and luminosity at a given binary separation.

As a crude approximation we could simply use the quadrupole formula, equation (9.37),

but we can do better than that. We can substitute the quasiequilibrium matter proﬁles that

we obtained above as source terms in the Einstein ﬁeld equations, and then evolve these

equations. In effect, we are performing a relativistic hydrodynamics simulation without

having to resolve the hydrodynamic equations, given that the matter is in near equilibrium.

This approach is sometimes referred to as “hydro-without-hydro”.

Evolving the gravitational ﬁelds for the given binary matter distribution, we can then

read off the gravitational waveform and luminosity, and hence the rate at which the binary

loses energy at a given separation r . Combining this luminosity dM

ADM

/dt =−L

with

the derivative of the ADM mass with respect to separation r along a quasiequilibrium

Similar ideas have been suggested as possible solutions to the “intermediate compact binary problem” that may arise

if (point-mass) post-Newtonian techniques, which are favored for the modeling of the adiabatic inspiral phase, break

down at too large a binary separation for fully dynamical numerical relativity simulations to track the entire remaining

inspiral. Bridging the resulting gap between post-Newtonian and numerical relativity methods might then require some

“quasiadiabatic” technique similar to the one sketched in this section to treat the full inspiral phase (see Brady et al.

(1998) and Duez et al. 2002).

See Baumgarte et al. (1999).