Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

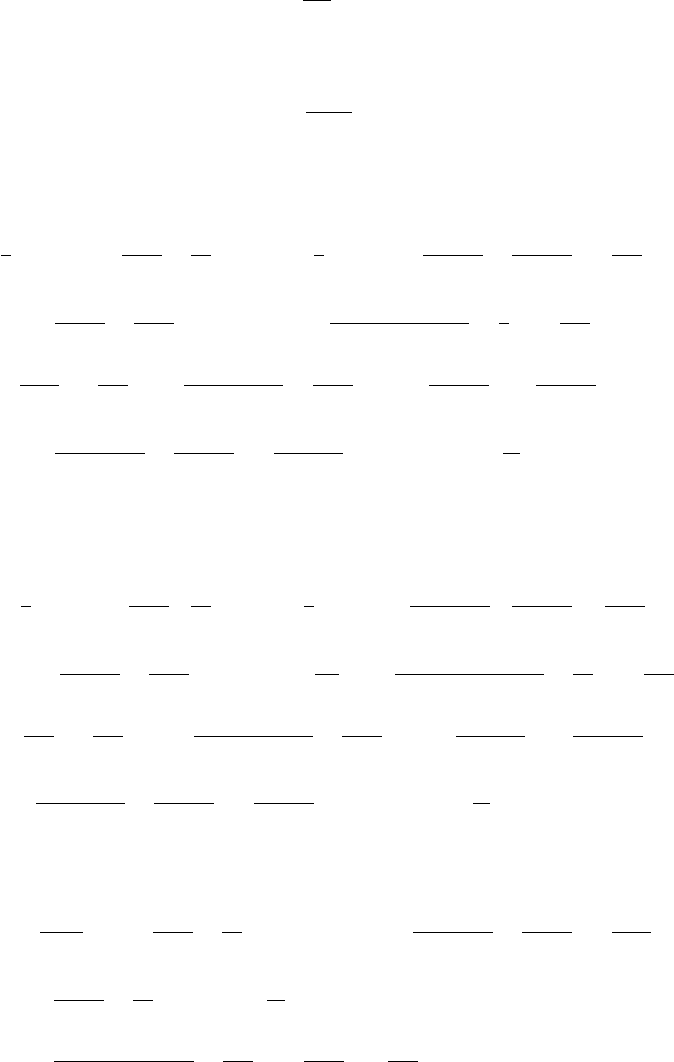
Appendix E Post-Newtonian results 621

to ﬁnd x, and hence ω, as a function of time. Since

d

dt

= ω, (E.18)

a further integration then yields the phase . It is convenient to express these results in terms of

a dimensionless measure of time,

 ≡

νc

3

5GM

(T − t), (E.19)

where T denotes the time of coalescence, at which point the angular speed ω diverges. Clearly, we

should abandon post-Newtonian methods well before this time. The ﬁrst integration now yields

x in terms of ,

x =

1

4



−1/4



1+



743

4032

+

11

48

ν





−1/4

−

1

5

π

−3/8

+



19583

254016

+

24401

193536

ν +

31

288

ν

2





−1/2

+



−

11891

53760

+

109

1920

ν



π

−5/8

+



−

10052469856691

6008596070400

+

1

6

π

2

+

107

420

C

−

107

3360

ln





256



+



3147553127

780337152

−

451

3072

π

2



ν −

15211

442368

ν

2

+

25565

331776

ν

3





−3/4

+



−

113868647

433520640

−

31821

143360

ν +

294941

3870720

ν

2



π

−7/8

+ O



1

c

8





. (E.20)

It is easy to verify that the leading-order term again agrees with the weak-ﬁeld, slow-velocity

result, which we derived in exercise 12.3. Integrating this expression again then yields the phase

 in terms of ,

 =−

1

ν



5/8



1+



3715

8064

+

55

96

ν





−1/4

−

3

4

π

−3/4

+



9275495

14450688

+

284875

258048

ν +

1855

2048

ν

2





−1/2

+



−

38645

172032

+

65

2048

ν



π

−5/8

ln





0



+



831032450749357

57682522275840

−

53

40

π

2

−

107

56

C

+

107

448

ln





256



+



−

126510089885

4161798144

+

2255

2048

π

2



ν +

154565

1835008

ν

2

−

1179625

1769472

ν

3





−3/4

+



188516689

173408256

+

488825

516096

ν −

141769

516096

ν

2



π

−7/8

+ O



1

c

8





. (E.21)

Here 

0

is a constant of integration that can be ﬁxed by the initial conditions. It is also possible

to combine the last two results and obtain the phase  in terms of the angular speed x,

 =−

x

−5/2

32ν



1 +



3715

1008

+

55

12

ν



x − 10π x

3/2

+



15293365

1016064

+

27145

1008

ν +

3085

144

ν

2



x

2

+



38645

1344

−

65

16

ν



π x

5/2

ln



x

0



+



12348611926451

18776862720

−

160

3

π

2

−

1712

21

C −

856

21

ln(16 x)

622 Appendix E Post-Newtonian results

+



−

15737765635

12192768

+

2255

48

π

2



ν +

76055

6912

ν

2

−

127825

5184

ν

3



x

3

+



77096675

2032128

+

378515

12096

ν −

74045

6048

ν

2



π x

7/2

+ O



1

c

8





, (E.22)

where x

0

is another constant of integration.

Finally we list the two gravitational wave polarization amplitudes h

+

and h

×

. Following

Blanchet et al. (2008) we write these as

h

+,×

=

2Gµx

c

2

r

H

+,×

+ O



1

r

2



, (E.23)

where r is the distance to the binary, and expand

H

+,×

=

∞



n=0

x

n/2

H

(n/2)

+,×

. (E.24)

To order 3PN, the coefﬁcients of the “+” polarization are given by

11

H

(0)

+

=−(1 + c

2

i

) cos 2ψ −

1

96

s

2

i

(17 + c

2

i

) , (E.25)

H

(0.5)

+

=−s

i



&

cos ψ



5

8

+

1

8

c

2

i



− cos 3ψ



9

8

+

9

8

c

2

i

'

, (E.26)

H

(1)

+

= cos 2ψ

&

19

6

+

3

2

c

2

i

−

1

3

c

4

i

+ ν



−

19

6

+

11

6

c

2

i

+ c

4

i

'

−cos 4ψ

&

4

3

s

2

i

(1 + c

2

i

)(1 − 3ν)

'

, (E.27)

H

(1.5)

+

= s

i

 cos ψ

&

19

64

+

5

16

c

2

i

−

1

192

c

4

i

+ ν



−

49

96

+

1

8

c

2

i

+

1

96

c

4

i

'

+cos 2ψ

$

−2π(1 + c

2

i

)

%

+s

i

 cos 3ψ

&

−

657

128

−

45

16

c

2

i

+

81

128

c

4

i

+ ν



225

64

−

9

8

c

2

i

−

81

64

c

4

i

'

+s

i

 cos 5ψ

&

625

384

s

2

i

(1 + c

2

i

)(1 − 2ν)

'

, (E.28)

H

(2)

+

= π s

i

 cos ψ

&

−

5

8

−

1

8

c

2

i

'

+cos 2ψ

&

11

60

+

33

10

c

2

i

+

29

24

c

4

i

−

1

24

c

6

i

+ ν



353

36

− 3 c

2

i

−

251

72

c

4

i

+

5

24

c

6

i



+ ν

2



−

49

12

+

9

2

c

2

i

−

7

24

c

4

i

−

5

24

c

6

i

'

11

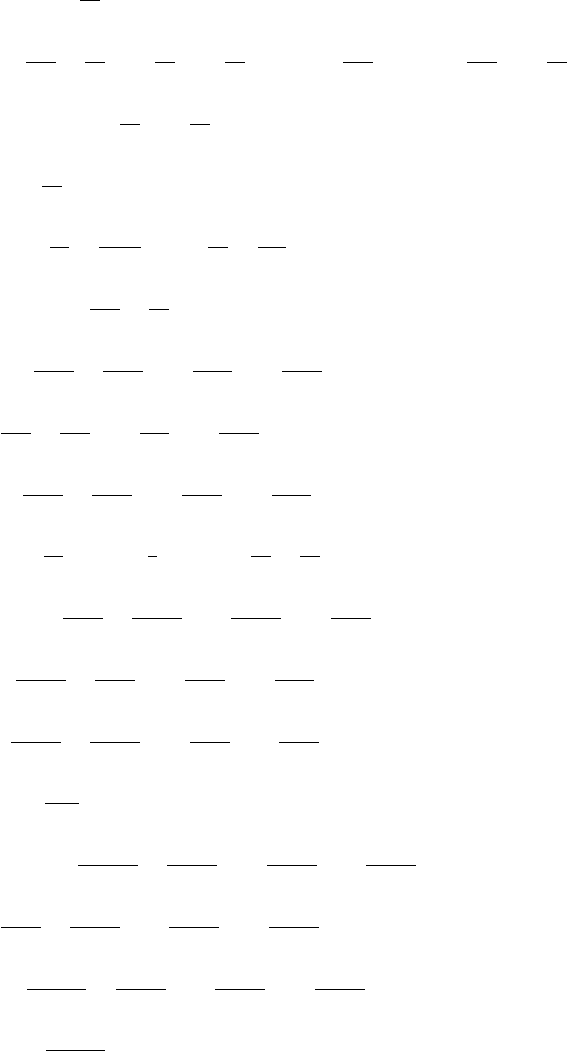
Note that the nonlinear memory (DC) term is included in the lowest order (“Newtonian”) H

(0)

+

term. For a discussion

see Arun et al. (2004).

Appendix E Post-Newtonian results 623

+π s

i

 cos 3ψ

&

27

8

(1 + c

2

i

)

'

+cos 4ψ

&

118

15

−

16

5

c

2

i

−

86

15

c

4

i

+

16

15

c

6

i

+ ν



−

262

9

+ 16 c

2

i

+

166

9

c

4

i

−

16

3

c

6

i



+ ν

2



14 − 16 c

2

i

−

10

3

c

4

i

+

16

3

c

6

i

'

+cos 6ψ

&

−

81

40

s

4

i

(1 + c

2

i

)



1 − 5ν + 5ν

2



'

+s

i

 sin ψ

&

11

40

+

5ln2

4

+ c

2

i



7

40

+

ln 2

4

'

+s

i

 sin 3ψ

&

−

189

40

+

27

4

ln(3/2)



(1 + c

2

i

)

'

, (E.29)

H

(2.5)

+

= s

i

 cos ψ

&

1771

5120

−

1667

5120

c

2

i

+

217

9216

c

4

i

−

1

9216

c

6

i

+ ν



681

256

+

13

768

c

2

i

−

35

768

c

4

i

+

1

2304

c

6

i



+ν

2



−

3451

9216

+

673

3072

c

2

i

−

5

9216

c

4

i

−

1

3072

c

6

i

'

+π cos 2ψ

&

19

3

+ 3 c

2

i

−

2

3

c

4

i

+ ν



−

16

3

+

14

3

c

2

i

+ 2 c

4

i

'

+s

i

 cos 3ψ

&

3537

1024

−

22977

5120

c

2

i

−

15309

5120

c

4

i

+

729

5120

c

6

i

+ ν



−

23829

1280

+

5529

1280

c

2

i

+

7749

1280

c

4

i

−

729

1280

c

6

i



+ ν

2



29127

5120

−

27267

5120

c

2

i

−

1647

5120

c

4

i

+

2187

5120

c

6

i

'

+ cos 4ψ

&

−

16π

3

(1 + c

2

i

) s

2

i

(1 − 3ν)

'

+s

i

 cos 5ψ

&

−

108125

9216

+

40625

9216

c

2

i

+

83125

9216

c

4

i

−

15625

9216

c

6

i

+ ν



8125

256

−

40625

2304

c

2

i

−

48125

2304

c

4

i

+

15625

2304

c

6

i



+ ν

2



−

119375

9216

+

40625

3072

c

2

i

+

44375

9216

c

4

i

−

15625

3072

c

6

i

'

+ cos 7ψ

&

117649

46080

s

5

i

(1 + c

2

i

)(1 − 4ν + 3ν

2

)

'

624 Appendix E Post-Newtonian results

+sin 2ψ

&

−

9

5

+

14

5

c

2

i

+

7

5

c

4

i

+ ν



32 +

56

5

c

2

i

−

28

5

c

4

i

'

+s

2

i

(1 + c

2

i

)sin4ψ

&

56

5

−

32 ln 2

3

+ ν



−

1193

30

+ 32 ln 2

'

, (E.30)

H

(3)

+

= πs

i

cos ψ

&

19

64

+

5

16

c

2

i

−

1

192

c

4

i

+ ν



−

19

96

+

3

16

c

2

i

+

1

96

c

4

i

'

+ cos 2ψ

&

−

465497

11025

+



856 C

105

−

2 π

2

3

+

428

105

ln(16 x)



(1 + c

2

i

)

−

3561541

88200

c

2

i

−

943

720

c

4

i

+

169

720

c

6

i

−

1

360

c

8

i

+ ν



2209

360

−

41π

2

96

(1 + c

2

i

) +

2039

180

c

2

i

+

3311

720

c

4

i

−

853

720

c

6

i

+

7

360

c

8

i



+ ν

2



12871

540

−

1583

60

c

2

i

−

145

108

c

4

i

+

56

45

c

6

i

−

7

180

c

8

i



+ν

3



−

3277

810

+

19661

3240

c

2

i

−

281

144

c

4

i

−

73

720

c

6

i

+

7

360

c

8

i

'

+πs

i

cos 3ψ

&

−

1971

128

−

135

16

c

2

i

+

243

128

c

4

i

+ ν



567

64

−

81

16

c

2

i

−

243

64

c

4

i

'

+s

2

i

cos 4ψ

&

−

2189

210

+

1123

210

c

2

i

+

56

9

c

4

i

−

16

45

c

6

i

+ ν



6271

90

−

1969

90

c

2

i

−

1432

45

c

4

i

+

112

45

c

6

i



+ ν

2



−

3007

27

+

3493

135

c

2

i

+

1568

45

c

4

i

−

224

45

c

6

i



+ν

3



161

6

−

1921

90

c

2

i

−

184

45

c

4

i

+

112

45

c

6

i

'

+ cos 5ψ

&

3125 π

384

s

3

i

(1 + c

2

i

)(1 − 2ν)

'

+s

4

i

cos 6ψ

&

1377

80

+

891

80

c

2

i

−

729

280

c

4

i

+ ν



−

7857

80

−

891

16

c

2

i

+

729

40

c

4

i



+ ν

2



567

4

+

567

10

c

2

i

−

729

20

c

4

i



+ν

3



−

729

16

−

243

80

c

2

i

+

729

40

c

4

i

'

+ cos 8ψ

&

−

1024

315

s

6

i

(1 + c

2

i

)(1 − 7ν + 14ν

2

− 7ν

3

)

'

+ s

i

sin ψ

&

−

2159

40320

−

19 ln 2

32

+



−

95

224

−

5ln2

8



c

2

i

+



181

13440

+

ln 2

96



c

4

i

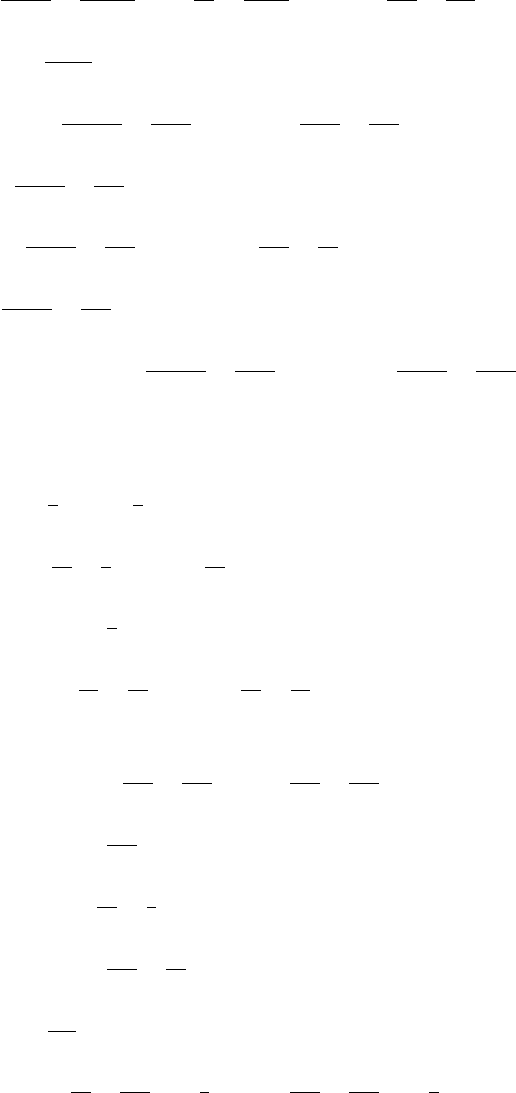
Appendix E Post-Newtonian results 625

+ν



81127

10080

+

19 ln 2

48

+



−

41

48

−

3ln2

8



c

2

i

+



−

313

480

−

ln 2

48



c

4

i

'

+ sin 2ψ

&

−

428 π

105

(1 + c

2

i

)

'

+ s

i

sin 3ψ

&

205119

8960

−

1971

64

ln(3/2) +



1917

224

−

135

8

ln(3/2)



c

2

i

+



−

43983

8960

+

243

64

ln(3/2)



c

4

i

+ ν



−

54869

960

+

567

32

ln(3/2) +



−

923

80

−

81

8

ln(3/2)



c

2

i

+



41851

2880

−

243

32

ln(3/2)



c

4

i

'

(E.31)

+ s

3

i

(1 + c

2

i

)sin5ψ

&

−

113125

5376

+

3125

192

ln(5/2) + ν



17639

320

−

3125

96

ln(5/2)

'

,

while the coefﬁcients for the cross-polarization are

H

(0)

×

=−2c

i

sin 2ψ, (E.32)

H

(0.5)

×

= s

i

c

i



&

−

3

4

sin ψ +

9

4

sin 3ψ

'

, (E.33)

H

(1)

×

= c

i

sin 2ψ

&

17

3

−

4

3

c

2

i

+ ν



−

13

3

+ 4 c

2

i

'

+c

i

s

2

i

sin 4ψ

&

−

8

3

(1 − 3ν)

'

, (E.34)

H

(1.5)

×

= s

i

c

i

 sin ψ

&

21

32

−

5

96

c

2

i

+ ν



−

23

48

+

5

48

c

2

i

'

−4π c

i

sin 2ψ

+s

i

c

i

 sin 3ψ

&

−

603

64

+

135

64

c

2

i

+ ν



171

32

−

135

32

c

2

i

'

+s

i

c

i

 sin 5ψ

&

625

192

(1 − 2ν) s

2

i

'

, (E.35)

H

(2)

×

= s

i

c

i

 cos ψ

&

−

9

20

−

3

2

ln 2

'

+s

i

c

i

 cos 3ψ

&

189

20

−

27

2

ln(3/2)

'

−s

i

c

i



&

3 π

4

'

sin ψ

+c

i

sin 2ψ

&

17

15

+

113

30

c

2

i

−

1

4

c

4

i

+ ν



143

9

−

245

18

c

2

i

+

5

4

c

4

i



626 Appendix E Post-Newtonian results

+ ν

2



−

14

3

+

35

6

c

2

i

−

5

4

c

4

i

'

+s

i

c

i

 sin 3ψ

&

27π

4

'

+c

i

sin 4ψ

&

44

3

−

268

15

c

2

i

+

16

5

c

4

i

+ ν



−

476

9

+

620

9

c

2

i

− 16 c

4

i



+ ν

2



68

3

−

116

3

c

2

i

+ 16 c

4

i

'

+c

i

sin 6ψ

&

−

81

20

s

4

i

(1 − 5ν + 5ν

2

)

'

, (E.36)

H

(2.5)

×

=

6

5

s

2

i

c

i

ν

+c

i

cos 2ψ

&

2 −

22

5

c

2

i

+ ν



−

282

5

+

94

5

c

2

i

'

+c

i

s

2

i

cos 4ψ

&

−

112

5

+

64

3

ln 2 + ν



1193

15

− 64 ln 2

'

+s

i

c

i

 sin ψ

&

−

913

7680

+

1891

11520

c

2

i

−

7

4608

c

4

i

+ ν



1165

384

−

235

576

c

2

i

+

7

1152

c

4

i



+ ν

2



−

1301

4608

+

301

2304

c

2

i

−

7

1536

c

4

i

'

+π c

i

sin 2ψ

&

34

3

−

8

3

c

2

i

+ ν



−

20

3

+ 8 c

2

i

'

+s

i

c

i

 sin 3ψ

&

12501

2560

−

12069

1280

c

2

i

+

1701

2560

c

4

i

+ ν



−

19581

640

+

7821

320

c

2

i

−

1701

640

c

4

i



+ ν

2



18903

2560

−

11403

1280

c

2

i

+

5103

2560

c

4

i

'

+s

2

i

c

i

sin 4ψ

&

−

32π

3

(1 − 3ν)

'

+ s

i

c

i

sin 5ψ

&

−

101875

4608

+

6875

256

c

2

i

−

21875

4608

c

4

i

+ ν



66875

1152

−

44375

576

c

2

i

+

21875

1152

c

4

i



+ ν

2



−

100625

4608

+

83125

2304

c

2

i

−

21875

1536

c

4

i

'

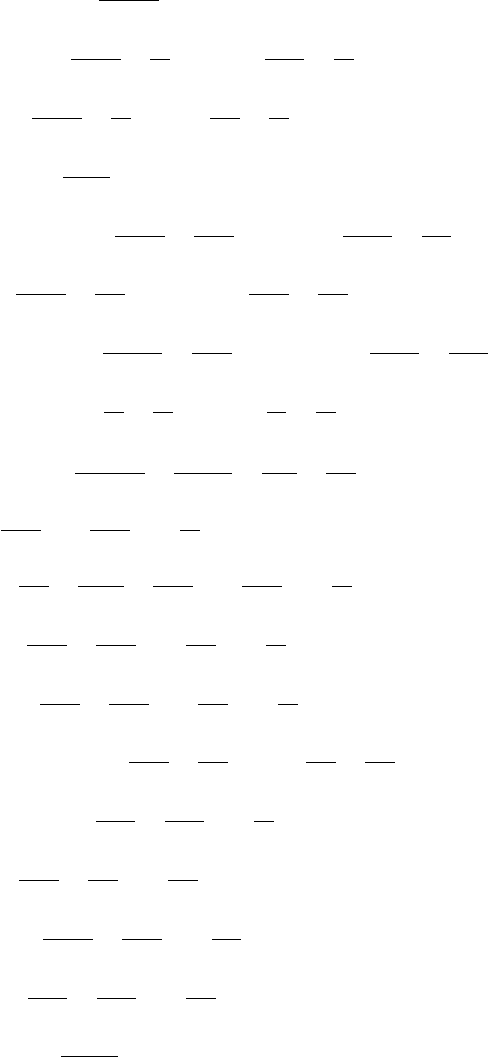
Appendix E Post-Newtonian results 627

+ s

5

i

c

i

sin 7ψ

&

117649

23040



1 − 4ν + 3ν

2



'

, (E.37)

H

(3)

×

=  s

i

c

i

cos ψ

&

11617

20160

+

21

16

ln 2 +



−

251

2240

−

5

48

ln 2



c

2

i

+ν



−

48239

5040

−

5

24

ln 2 +



727

240

+

5

24

ln 2



c

2

i

'

.

+c

i

cos 2ψ

&

856 π

105

'

+ s

i

c

i

cos 3ψ

&

−

36801

896

+

1809

32

ln(3/2) +



65097

4480

−

405

32

ln(3/2)



c

2

i

+ν



28445

288

−

405

16

ln(3/2) +



−

7137

160

+

405

16

ln(3/2)



c

2

i

'

+ s

3

i

c

i

cos 5ψ

&

113125

2688

−

3125

96

ln(5/2) + ν



−

17639

160

+

3125

48

ln(5/2)

'

+πs

i

c

i

sin ψ

&

21

32

−

5

96

c

2

i

+ ν



−

5

48

+

5

48

c

2

i

'

+c

i

sin 2ψ

&

−

3620761

44100

+

1712 C

105

−

4 π

2

3

+

856

105

ln(16 x)

−

3413

1260

c

2

i

+

2909

2520

c

4

i

−

1

45

c

6

i

+ ν



743

90

−

41 π

2

48

+

3391

180

c

2

i

−

2287

360

c

4

i

+

7

45

c

6

i



+ ν

2



7919

270

−

5426

135

c

2

i

+

382

45

c

4

i

−

14

45

c

6

i



+ν

3



−

6457

1620

+

1109

180

c

2

i

−

281

120

c

4

i

+

7

45

c

6

i

'

+πs

i

c

i

sin 3ψ

&

−

1809

64

+

405

64

c

2

i

+ ν



405

32

−

405

32

c

2

i

'

+s

2

i

c

i

sin 4ψ

&

−

1781

105

+

1208

63

c

2

i

−

64

45

c

4

i

+ ν



5207

45

−

536

5

c

2

i

+

448

45

c

4

i



+ ν

2



−

24838

135

+

2224

15

c

2

i

−

896

45

c

4

i



+ν

3



1703

45

−

1976

45

c

2

i

+

448

45

c

4

i

'

+ sin 5ψ

&

3125 π

192

s

3

i

c

i

(1 − 2ν)

'

628 Appendix E Post-Newtonian results

+s

4

i

c

i

sin 6ψ

&

9153

280

−

243

35

c

2

i

+ ν



−

7371

40

+

243

5

c

2

i



+ν

2



1296

5

−

486

5

c

2

i



+ ν

3



−

3159

40

+

243

5

c

2

i

'

+ sin 8ψ

&

−

2048

315

s

6

i

c

i

(1 − 7ν + 14ν

2

− 7ν

3

)

'

. (E.38)

We have used several new quantities and abbreviations in the above expressions. The phase

variable ψ is related to the orbital phase  by

ψ =  −

2GM

ADM

ω

c

3

ln



ω

0



, (E.39)

where

M

ADM

= m



1 −

νγ

2



+ O



1

c

4



(E.40)

is the ADM mass, and where ω

0

is some arbitrary constant frequency. It could be chosen, for

example, to be the entry frequency of a gravitational wave detector. We also use the dimensionless

mass difference  = (m

1

− m

2

)/M, and the abbreviations c

i

= cos i and s

i

= sin i, where i is

the inclination angle between the binary’s axis of rotation and the direction to the observer. The

waveforms can also be decomposed into spin-weighted tensor spherical harmonics, but we shall

refer the reader elsewhere for the expressions and further details.

12

Before closing this appendix we mention two alternative “resummation” techniques that have

been suggested to enhance the convergence of post-Newtonian approximations. Our description

above outlines the construction of a post-Newtonian approximation as a Taylor expansion in the

parameters γ or x (see equations E.10 or E.13). Such a polynomial expansion can converge

well only in the absence of poles in the functions that we aim to approximate. For small binary

separations, however, poles may appear. It has therefore been suggested that one construct,

from the information contained in the polynomial expansion, an expansion in terms of rational

functions.

13

The resulting expansion is an example of a so-called Pad

´

e approximant, which

sometimes converges faster than the corresponding Taylor expansion.

14

In yet another approach, the general relativistic binary problem is mapped onto that of a

test particle moving in an effective external metric, thereby reducing a two-body problem to an

effective one-body (EOB) problem.

15

Starting with a post-Newtonian expansion for the relativistic

two-body equations of motion, this approach may be viewed as a nonperturbative means of

resumming the post-Newtonian expressions. In Chapter 12.4 we have included EOB results in

our comparison with post-Newtonian predictions for locating the innermost stable circular orbit

for binary black holes.

12

See Blanchet et al. (2008).

13

See Damour et al. (1998).

14

See, e.g., Press et al. (2007) for a brief introduction.

15

See Buonanno and Damour (1999).

F

Collisionless matter

evolution in axisymmetry:

basic equations

Here we list the key equations describing a mean-ﬁeld, particle simulation scheme that can treat

the evolution of collisionless matter in axisymmetry according to general relativity.

1

The scheme

is a generalization of the one described in Chapter 8.2 for spherical systems and employs the

standard ADM form of the ﬁeld equations as listed in Box 2.1. We adopt spherical polar space-

time coordinates (t, r,θ,φ), assume axisymmetry and specialize to the case where there is no

net angular momentum.

2

In axisymmetry all quantities are functions only of (t, r,θ). We also

impose maximal slicing and quasi-isotropic spatial coordinates as our gauge conditions.

3

This

spatial gauge condition reduces to isotropic coordinates for Schwarzschild geometry.

4

The ﬁeld

equations listed below constitute a fully constrained approach to solving the Einstein ﬁeld equa-

tions for this problem, i.e., one which solves all of the constraint equations in lieu of integrating

evolution equations for some of the variables. Fully constraint schemes have the advantage over

unconstrained schemes that the constraints are guaranteed to be satisﬁed at all times, which may

in some cases also eliminate some instabilities associated with the evolution equations. Their

disadvantage is that the constraints constitute elliptic equations, which typically require more

computational resources to solve than explicit time evolution equations. This disadvantage is not

so severe, however, in 1 +1or2+ 1 spacetimes. A similar set of variables and ﬁeld equations to

the ones summarized below has been used to simulate the gravitational collapse of hydrodynamic

ﬂuids

5

and vacuum gravitational waves

6

in nonrotating, axisymmetric spacetimes, as well as the

head-on collision of neutron stars.

7

Gravitational ﬁeld equations

The metric is written as

ds

2

=−α

2

dt

2

+ A

2

(dr + β

r

dt)

2

+ A

2

r

2

(dθ + β

θ

dt)

2

+ B

2

r

2

sin

2

θdφ

2

. (F.1)

Here we used the fact that the absence of axial rotation demands invariance with respect to all

changes φ →−φ, which implies β

φ

= 0 = γ

rφ

= γ

θφ

. The simpliﬁed quasi-isotropic form of

1

Shapiro and Teukolsky (1991b, 1992a,b).

2

Evans (1984). For extension to rotating spacetimes, see Abrahams et al. (1994).

3

See Chapter 4 for a discussion.

4

For an alternative radial gauge choice, which reduces to Schwarzschild (areal) coordinates, see Bardeen and Piran

(1983) and Chapter 4.

5

See, e.g., Evans (1986).

6

Abrahams and Evans (1993).

7

Abrahams and Evans (1992).

629

630 Appendix F Collisionless matter evolution in axisymmetry

the 3-metric γ

ij

= diag(A

2

, A

2

r

2

, B

2

r

2

sin

2

θ) results from imposing the gauge conditions

∂

t

γ

rθ

= 0,∂

t

(r

2

γ

rr

− γ

θθ

) = 0, (F.2)

with initial conditions

γ

rθ

= 0, r

2

γ

rr

− γ

θθ

= 0. (F.3)

In addition to the metric coefﬁcients α, β

r

, β

θ

, A and B, we need to determine the components

of the extrinsic curvature tensor, K

i

j

. It is convenient to introduce the related quantities

ˆ

K

i

j

≡ A

2

BK

i

j

, (F.4)

and similarly for all other variables with a caret (i.e., all quantities with a caret are related to

“uncareted” quantities by a factor A

2

B).

The evolution equations are used to determine the “radiation variables” η ≡ ln(A/B) and

ˆ

K

r

θ

according to

∂

t

η =

α

A

2

B

ˆ

λ + β

r

∂

r

η + β

θ

∂

θ

η + ∂

θ

β

θ

− β

θ

cot θ, (F.5)

∂

t

ˆ

K

r

θ

=

1

r

2

∂

r

(r

2

β

r

ˆ

K

r

θ

) +

1

sin θ

∂

θ

(sin θβ

θ

ˆ

K

r

θ

)

−

α A

r sin θ



∂

θ

&

sin θ

A

∂

r

(Br)

'

−

1

A

2

∂

r

(Ar)∂

θ

(B sin θ)

-

+

ˆ

K

r

θ

(∂

θ

β

θ

− ∂

r

β

r

) + (2

ˆ

λ − 3

ˆ

K

φ

)∂

θ

β

r

− AB∂

θ



1

A

∂

r

α



+

B

Ar

∂

r

(Ar)∂

θ

α −

α

A

2

ˆ

S

rθ

, (F.6)

where

ˆ

λ ≡

ˆ

K

r

+ 2

ˆ

K

φ

, (F.7)

and where matter source terms like

ˆ

S

rθ

will be deﬁned below.

The momentum constraint equations, which we use to solve for

ˆ

K

r

,are

1

sin θ

∂

θ

(sin θ

ˆ

K

r

) +

T

sin

2

θ

∂

θ



sin

2

θ

T

ˆ

K

φ



=−

ˆ

S

θ

+

1

r

2

∂

r

(r

2

ˆ

K

r

θ

), (F.8)

1

r

3

∂

r

(r

3

ˆ

K

r

) +

ˆ

K

φ

∂

r

η =

ˆ

S

r

−

1

r

2

sin θ

∂

θ

(sin θ

ˆ

K

r

θ

), (F.9)

where T ≡ A/B. The Hamiltonian constraint yields an elliptic equation for ψ ≡ B

1/2

,

1

r

2

∂

r

(r

2

∂

r

ψ) +

1

r

2

sin θ

∂

θ

(sin θ∂

θ

ψ) =−

1

4

ψ

&

1

r

∂

r

(r∂

r

η) +

1

r

2

∂

2

θ

η

+

1

T

2

ψ

8



ˆ

λ

2

− 3

ˆ

λ

ˆ

K

φ

+ 3(

ˆ

K

φ

)

2

+



ˆ

K

r

θ

/r



2

-'

−

ˆρ

4ψ

. (F.10)

Maximal slicing ∂

t

K = 0 = K yields an elliptic equation for the lapse, which we combine

with the Hamiltonian constraint (F. 1 0 ) to obtain an elliptic equation for αψ,

1

r

2

∂

r

[r

2

∂

r

(αψ)] +

1

r

2

sin θ

∂

θ

[sin θ∂

θ

(αψ)] =

1

4

αψ

&

−

1

r

∂

r

(r∂

r

η) −

1

r

2

∂

2

θ

η

+

7

A

2

B

2



ˆ

λ

2

− 3

ˆ

λ

ˆ

K

φ

+ 3(

ˆ

K

φ

)

2

+



ˆ

K

r

θ

/r



2

-

+

1

B

(ˆρ + 2

ˆ

S)

'

. (F.11)

Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.