Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

17.2 Dynamical simulations 591

100

−23

−22

−21

−23

−22

−21

BHNS: NR+2.5PN

BHNS: NR

BHBS

Advanced LIGO

−23

−22

−21

Case E

Case A

Case D

1000

[Hz]

eff

[D = 100Mpc]

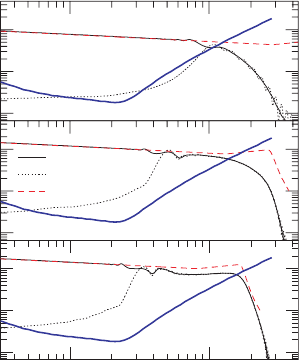
Figure 17.12 Gravitational wave power spectra for the q = 1, 3, and 5 cases (cases E, A, and D, respectively).

The solid curve in each panel shows the combined waveform found by attaching the restricted 2.5 order PN

waveform to the dominant modes computed by the numerical relativity simulation (NR), while the dotted curve

shows the contribution from the latter alone. The dashed curve shows the power spectrum for a nonspinning

black hole binary merger (BHBH) for black holes with the same mass ratios as the black hole–neutron star

binaries (BHNS); the later exhibit signiﬁcantly less power at higher frequencies, due to tidal disruption. The

heavier solid curve is the effective strain of the Advanced LIGO detector, deﬁned by h

LIGO

( f )(seetext).Toset

physical units, we assume a neutron star rest mass of M

= 1.4M



and a source distance of D = 100 Mpc.

[From Etienne et al. (2009).]

star is assumed to have a rest-mass of 1.4M



and the binary is placed at a distance of

100 Mpc. This is the distance required to reach one merger per year in one estimate,

assuming an overall rate of 10 mergers per Myr per Milky Way-equivalent galaxy (and

a density of these of 0.1 gal/Mpc

). This distance is roughly that of the Coma cluster,

and approximately ﬁve times the distance to the Virgo cluster. The gravitational wave

spectra of nonspinning binary black hole mergers with the same mass ratios as in the

three black hole–neutron star cases are also plotted for comparison. The ﬁgure shows

that the wave signal drops appreciably near the frequency corresponding to the onset

of neutron star tidal disruption. The difference in wave signals between binary black

hole and black hole mergers is seen to be marginally observable in the Advanced LIGO

frequency band in most cases. Distinguishing binary black hole from binary black hole–

neutron star inspirals and mergers may thus require narrow-band wave detection techniques

with advanced detectors. The observation of an accompanying GRB would also serve to

distinguish the two types of events (and would be a dramatic discovery!). Should the chirp

mass determination, combined with higher order PN waveform phase effects, allow for an

Belczynski et al. (2002).

−2−4−6−8

−8

−6

−4

−2

Y / M

X / M

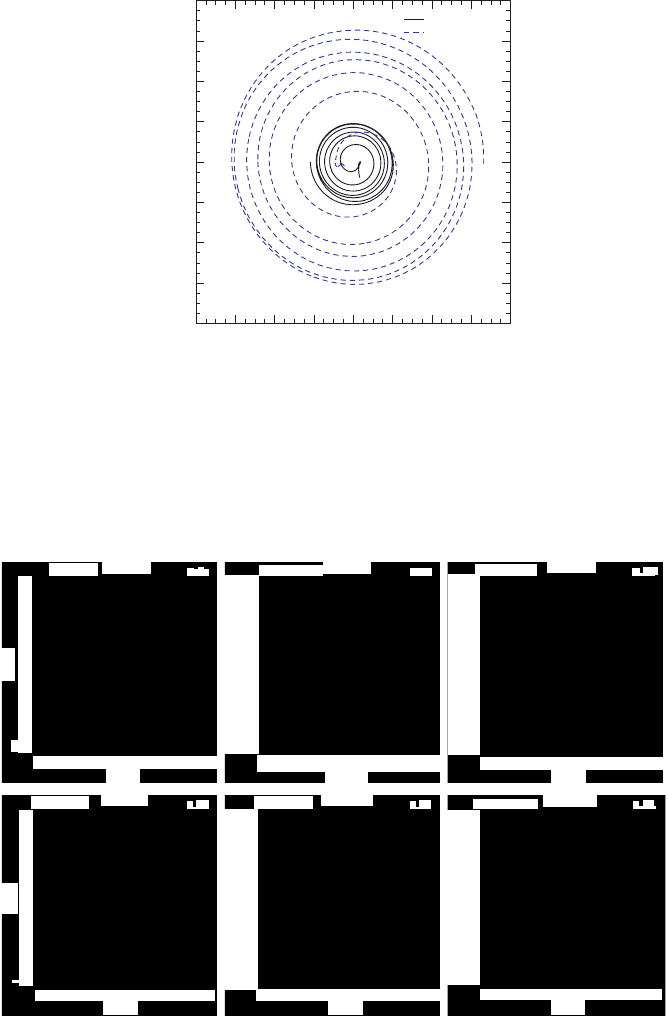
Figure 17.13 Trajectories of the black hole and neutron star coordinate centroids for the merger of an

irrotational neutron star orbiting a spinning black hole with spin J

= 0.75 (case B). Compare with

Figure 17.8 for the merger of an identical neutron star with a nonspinning black hole, assuming the same binary

mass ratio q = 3 and initial orbital angular velocity M ≈ 0.033. [From Etienne et al. (2009).]

t = 0.0M

t = 616. 7M

Case B

0.5c

t = 722.7M

Case B

0.5c

t = 1878.5M

Case B

0.5c

t = 998.9M

Case B

0.5c

t = 847.5M

Case B

0.5c

Y / MY / M

X / M X / M

−5

−10

−5

−10

X / M

−5

−10

X / M

−5

−10

X / M

−5

−10

X / M

−5

−10

Figure 17.14 Snapshots of rest-density contours and 3-velocity vectors at selected times during the merger of

an irrotational neutron star orbiting a black hole with spin a/M

= J

= 0.75, as shown in Figure 17.13

(case B). The contours represent the density in the orbital plane, plotted according to

= ρ

0,max

−0.38 j−0.04

, ( j = 0, 1,...,12), with darker gray scaling for higher density. The maximum initial

neutron star density is Kρ

0,max

= 0.126, where K is the initial polytropic gas constant, or

0,max

= 9 × 10

g/cm

(1.4M



)

. Arrows represent the velocity ﬁeld in the orbital plane. The apparent

horizon interior is marked by a ﬁlled black circle. In cgs units, the initial ADM mass for this case is

M = 2.5 × 10

−5

/1.4M



)s= 7.6(M

/1.4M



) km. [From Etienne et al. (2009).]

17.2 Dynamical simulations 593

0.0

−0.5

Case A

Case B

Case C

0.1

0.01

0 200 400 600 800 1000

(t − t

)/ M

a/M

= 0.75

Fraction Outside AH

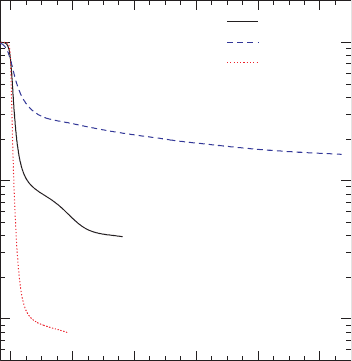
Figure 17.15 Rest-mass fraction outside the black hole as a function of time for the merger of an irrotational

neutron star orbiting a black hole with different initial black hole spins a/M

. Here the time coordinate is

shifted by t

, the time at which 25% of the neutron star rest-mass has fallen into the apparent horizon. [From

Etienne et al. (2009).]

independent determination of the individual masses and spins of the binary companions,

the measurement of the black hole-neutron star tidal disruption frequency should give a

good estimate of the neutron star radius and, hence, insight into the nuclear EOS.

Irrotational neutron stars with spinning black holes

Etienne et al. (2009) also explore the effects of black hole spin on the merger of black

hole–neutron star binaries. They consider irrotational neutron stars orbiting spinning black

holes, taking the black hole spins to be either aligned or anti-aligned with the orbital

angular momentum. They again use conformal thin-sandwich quasiequilibrium initial

data for the binaries and evolve models with the initial spin parameter of the black hole

between J

=−0.5 (anti-aligned) and 0.75, ﬁxing the mass ratio at q = 3 and the

initial orbital angular velocity at M ≈ 0.033. As the initial spin parameter increases,

the total initial angular momentum increases, requiring more gravitational wave cycles

to emit sufﬁcient angular momentum to bring the companions close enough to merge.

Not surprisingly, the binary undergoes more orbits before merger as J

increases:

for spins −0.5, 0.0, and 0.75, the binary inspiral phase lasts for 3.25, 4.5, and 6.5 orbits,

respectively. The coordinate trajectories of the apparent horizon and neutron star centroids

are shown in Figure 17.13 for the case with J

= 0.75 (case B).

Figure 17.14 shows snapshots of the density and velocity vectors at selected times during

the evolution for the J

= 0.75 case. The upper plots in the ﬁgure demonstrate that

the neutron star retains its shape for four orbits (upper middle), and begins shedding

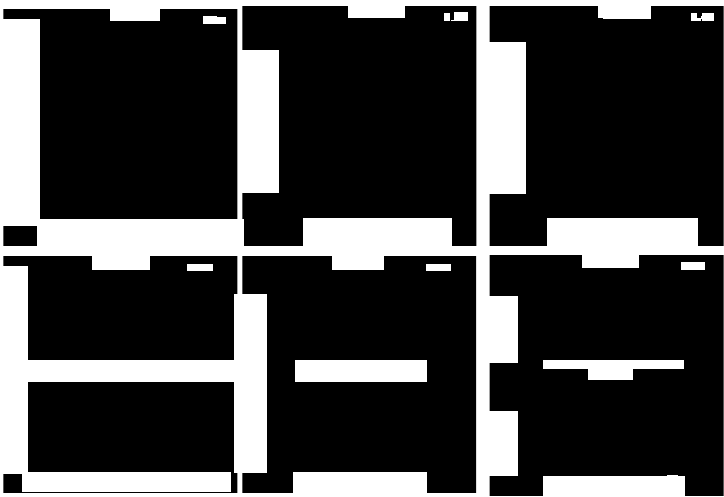
594 Chapter 17 Binary black hole–neutron stars

0.5c

Case E

X (km)

−20

−40

40200

−20−40

40200

−20−40

Case A

Case B

50 100

100

−100

−50

0.5c 0.5c

Y (km)

X (km) X (km)

0.5c 0.5c

0.5c

Case E Case A

−50

100

−100

100

−100

100

−50

Z (km)

X(km)

Y(km)

Figure 17.16 Snapshots of rest-density contours and 3-velocity vectors at the end of the simulations for three

binary black hole–neutron star merger scenarios (see text). The remnant disks are shown in the orbital plane

(upper row) and meridional plane (bottom rows). The contours represent the density plotted according to

= ρ

0,max

−0.1 j−3.3

( j = 0, 1,...,13) for cases A and B and ρ

= ρ

0,max

−0.19 j−2.32

( j = 0, 1,...,12) for

case E, with darker gray scaling for higher density. In all cases the maximum initial neutron star density is

Kρ

0,max

= 0.126, where K is the initial polytropic gas constant, or ρ

0,max

= 9 × 10

gcm

−3

(1.4M



)

Arrows represent the velocity ﬁeld. The apparent horizon interior in the orbital plane is marked by a ﬁlled black

circle. Length scales are speciﬁed in km, assuming the neutron star has a rest-mass of 1.4M



; it can be converted

to units of M via the formula M = 1.9(q + 1) km. [After Etienne et al. (2009).]

its outer layers due to tidal disruption only after about ﬁve orbits (upper right). In this

case the tail is quite massive (lower left), and by the time 75% of the mass has been

accreted (lower center) it is much larger than the tail measured at the same point for a

nonspinning black hole (lower left plot in Figure 17.9). The lower right plot is a snapshot

taken near the end of the simulation, when a quasistationary disk resides outside the BH.

The disk is massive: M

disk

≈ 15%, corresponding to 0.2M



for a 1.4M



neutron

star. The maximum density of the disk is ρ

0,max

≈ 5 × 10

gcm

−3

and the characteristic

temperature is T ∼ 5 × 10

K(or∼4 MeV), values which are similar to the nonspinning

case. However, the disk is about twice as large in size, with a characteristic radius of

disk

= 100 km, in addition to being much more massive.

Etienne et al. (2009) conclude from their simulations that the black hole-neutron star

inspiral phase lasts longer the larger the spin J

. Also, larger aligned spins form

more extensive and more massive disks: the ﬁnal disk mass grows from < 1% of the initial

neutron star rest mass when the black hole has a spin J

=−0.5 (case C) to ≈ 4%

17.2 Dynamical simulations 595

0.15

Case C

Case A

Case B

−0.15

200

(t − r

)/M

150 300

300

450

400

400200100

600

800

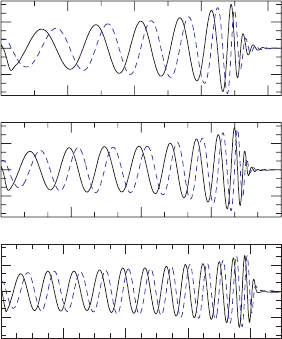
Figure 17.17 Gravitational wave signal for three binaries with mass ratio q = 3 and initial black hole spins (top

to bottom) J

=−0.5, 0, and 0.75. The black solid (blue dash) line denotes the (2,2) mode of h

)

extracted at r

= 43.4M.[FromEtienne et al. (2009).]

foraspinof0(caseA)to≈ 15% for a spin of 0.75 (case B). Figure 17.15 shows the rest

mass outside the black hole as a function of time for these three cases, illustrating once

again the two phases of mass consumption by the black hole. If the formation of a massive

disk about a rotating black hole is a prerequisite for a short-hard GRB, then it appears that

the more rapidly spinning and closely aligned the initial black hole, the more likely it is to

power such a source by binary black hole–neutron star merger.

A comparison between the ﬁnal disks formed in the three merger scenarios is shown in

Figure 17.16. Both the mass ratios and initial black hole spins are varied for a cross-the-

board comparison: recall that (q, J

) =(1, 0) for case E, (3, 0) for case A and (3,

0.75) for case B.

Finally, we show a comparison between gravitational waveforms emitted for three merger

scenarios in Figure 17.17. The mass ratios are all identical (q = 3) but the initial black

hole spins are varied: J

=−0.5 for case C, 0 for case A and 0.75 for case B.

Though tentalizing, all of these results are quite preliminary. Simulations that take

into account the detailed microphysics, including the correct hot, nuclear EOS, magnetic

ﬁelds and neutrino and photon transport, are necessary to fully assess the viability of and

mechanism for generating short-hard GRBs from binary black hole–neutron star mergers.

But much of the groundwork, especially the tool of numerical relativity, has been prepared

to carry out such simulations.

Epilogue

This is not the end.

It is not even the beginning of the end.

But it is, perhaps, the end of the beginning.

Winston Churchill (1942)

This brings us to the end of our introduction to numerical relativity. A quick glance

at the table of contents shows that we have covered a wide range of subjects, starting

with the foundations of numerical relativity and continuing with applications to different

areas of gravitational physics and astrophysics. Despite the breadth of our survey, we

have had to be selective in our choice of topics. Our focus has been on solving the

Cauchy problem in general relativity for dynamical, asymptotically ﬂat spacetimes, with

applications to compact objects and compact binaries. There are a number of alternative

approaches for solving Einstein’s equations that we did not touch on at all, such as the

characteristic approach and the Regge calculus. We also did not discuss in any detail

applications involving strictly stationary spacetimes, such as gas accretion onto Kerr black

holes, although some of the same schemes we described for matter evolution have been

used successfully to treat problems with ﬁxed background metrics. We trust that interested

readers will ﬁnd discussions of the subjects we omitted elsewhere in the literature.

We hope that our treatment laying out the foundations of numerical relativity will remain

relevant for the foreseeable future. However, we suspect that some of the large-scale

simulations we have chosen to illustrate different implementations will be superseded

by more sophisticated calculations. Such calculations will invariably incorporate more

detailed microphysics and will take advantage of more advanced computational algorithms

and hardware. Yet we would like to believe that, at the very least, the examples we have

selected to highlight will help preview and elucidate these more sophisticated, future

simulations. We invite our readers to assess this situation for themselves.

Exercise 18.1 Pick one of the applications of numerical relativity treated in this

book, such as binary neutron star mergers, or magnetorotational stellar collapse, or

one of the other topics. Perform a search of the recent computational literature to

determine what new physical input or methods of solution have been implemented

and what new results have emerged for this application since the writing of this

book.

596

Chapter 18 Epilogue 597

One exciting prospect is that numerical relativity will be applied to areas of gravitational

physics and astrophysics that have yet to take full advantage of this powerful computational

tool. It is possible, for example, that numerical relativity will prove useful to probe certain

aspects of cosmology where homogeneity is not applicable and where neither perturbation

theory nor Newtonian gravitation is adequate. It is also possible that numerical relativity

will play a greater role in investigating the higher-dimensional spacetimes that arise in

quantum ﬁeld theories, such as string theory. More than likely, there are areas that we

cannot even fathom now that will turn to numerical relativity in the future for computational

insight. We again leave it to future readers to identify such areas, or, even better, to lead

the charge!

Exercise 18.2 Do a casual search of the research literature and see if there are any

new applications of numerical relativity in physics or astrophysics that have not been

mentioned at all in this book.

Lie derivatives, Killing

vectors, and tensor densities

In this appendix we introduce a few of the mathematical concepts used in the book with which

some readers may be less familiar, namely, the Lie derivative, Killing vectors and tensor densities.

The aim of our presentation is to make these concepts transparent and easy to use in applications;

for a more complete and rigorous treatment we refer the reader to the discussions in, for example,

Schutz (1980) and Wald (1984).

A.1 The Lie derivative

Consider a (nonzero) vector ﬁeld X

in a manifold M.

We can ﬁnd the integral curves x

(λ)(or

orbits, or trajectories) of X

by integrating the ordinary differential equations

dλ

= X

(x(λ)). (A.1)

Here λ is some afﬁne parameter, and we use bold-face notation x instead of index notation x

for

the coordinate location in the argument to make the expressions more transparent. For a sufﬁciently

well-behaved vector ﬁeld X

a solution is guaranteed, at least locally, by the existence and

uniqueness theorem for ordinary differential equations. This procedure is completely equivalent

to ﬁnding the paths of ﬂuid particles, given their ﬂuid velocity. The integral curves x

(λ)are

now a family of curves in M, so that exactly one curve passes through each point in M (see

Figure A.1). Such a family is known as a congruence of curves. Obviously, at each point the

tangent to the integral curves is given by X

We would now like to deﬁne a derivative of a tensor ﬁeld, say T

,usingX

. This involves

comparing the tensor ﬁeld at two different points along X

,sayP and Q, and taking the limit as

Q tends to P. This is where we encounter a conceptual problem: what do we mean by comparing

two tensors at two different locations in the manifold M?

We could, of course, simply compare components of the tensor ﬁeld T

at P, T

(P) and at

Q, T

(Q). This leads to the deﬁnition of the partial derivative. Note, however, what happens

under a coordinate transformation. The tensors T

(P) and T

(Q) have to be transformed with

the transformation matrix evaluated at the two points P and Q. In general the two matrices will

be different, and, accordingly, the result of this differentiation cannot be a tensor. This is one way

to understand why the partial derivative of a tensor is not a tensor.

In order to differentiate a tensor in a tensorial manner, we therefore have to evaluate the two

tensors at the same point. To do so, we have to drag one tensor to the other point before we can

compare the two tensors. For example, we can drag T

(P) along X

to the point Q.AtQ,we

This section closely follows the discussion in d’Inverno (1992).

598

A.1 The Lie derivative 599

vector field

integral curves x

Figure A.1 A vector ﬁeld X

generates a congruence of curves x

drag

(P )

(

)

(P )

(Q )

Figure A.2 Dragging a tensor T

from P to Q.

can then compare the dragged tensor, which we will denote with primes, T



(Q), with the tensor

already present at Q, T

(Q) (see Figure A.2).

However, this recipe still leaves open how we drag T

along X

. One approach would be to

parallel-transport the tensor T

from P to Q. This idea leads to the deﬁnition of the covariant

derivative. Put into words, the covariant derivative measures by how much the changes in a tensor

ﬁeld along X

differ from being parallel-transported.

Parallel-transporting is not the only way of dragging T

along X

. In some sense an even more

straightforward approach is to view the dragging as a simple coordinate transformation from P to

Q. This, in fact, deﬁnes the Lie derivative. In other words, the Lie derivative along a vector ﬁeld

measures by how much the changes in a tensor ﬁeld along X

differ from a mere inﬁnitesimal

coordinate transformation generated by X

. Unlike the covariant derivative, the Lie derivative

does not require an afﬁne connection and hence requires less structure.

Consider now the inﬁnitesimal coordinate transformation



= x

+ δλ X

(x), (A.2)

which maps the point P, with coordinates x

, into the point Q, with coordinates x



.Weregard

this as an active coordinate transformation, which maps points (and tensors) to new locations in

the old coordinate system. Completely equivalently, a passive coordinate transformation assigns

new coordinate values to the old point.

Assuming a coordinate basis we can differentiate (A.2) to ﬁnd

∂x



∂x

= δ

+ δλ ∂

, (A.3)

600 Appendix A Lie derivatives, Killing vectors, and tensor densities

and, to ﬁrst order in δλ,

∂x



= δ

− δλ ∂

. (A.4)

We now start at point P, where the components of the tensor ﬁeld T

are T

(x). We map this

tensor into the primed tensor T



)atQ with the help of the coordinate transformation (A.2)



) =

∂x



∂x



(x)

= (δ

+ δλ ∂

)(δ

− δλ ∂

(x)

= T

(x) + δλ (∂

(x) − ∂

(x)) + O(δλ

). (A.5)

For the purpose of deﬁning the Lie derivative this is the result of dragging T

along X

from

P to Q. The components of the unprimed tensor already present at Q, T



), can be related to

(x) by Taylor expanding



) = T



) = T

+ δλ X

) = T

(x) + δλ X

∂

+ O(δλ

). (A.6)

We now denote the Lie derivative of T

with respect to X

as L

and deﬁne

≡ lim

δλ→0



) − T



)

δλ

(A.7)

This deﬁnition holds for any tensor of arbitrary rank and type (i.e., covariant and contravariant).

Note that we evaluate both tensors at the same point, so that the Lie derivative of a tensor is

again a tensor, and moreover a tensor of the same rank. Note also a subtlety of our abstract tensor

notation: The expression L

= (L

T )

implies that the Lie derivative of the tensor T

again a tensor of rank (

); it does not denote the Lie derivative of the a-b component of T

For our tensor T

of rank (

) we can insert (A.5) and (A.6)into(A.7) to ﬁnd

= X

∂

− T

∂

+ T

∂

. (A.8)

The Lie derivative of a general tensor ﬁeld can be found by ﬁrst taking a partial derivative of the

tensor and contracting it with X

, and then adding additional terms involving derivatives of X

as in (A.8) for each index, with a negative sign for contravariant indices and a positive sign for

covariant indices.

We can always introduce an adapted coordinate system, in which, for example, the coordinate

basis vector e

(0)

is aligned with X

, and all the other coordinates are constant along X

. Setting

= e

(0)

then yields

= δ

= (1, 0,...,0). (A.9)

We have used Greek indices as opposed to the Latin indices of our abstract index notation, since

this relationship for components only holds in these adapted coordinates. Writing equation (A.8)

in this coordinate system, we immediately ﬁnd

∂

∂x

. (A.10)

See also exercise (8.13) in Lightman et al. (1975).