Bear H.S. Understanding Calculus

Подождите немного. Документ загружается.

214

Understanding

Calculus

EXAMPLE 34.2

Graph

the

surface

z =

2~.

Solution

Thecross

sections

in theplanesz =

constant,

z 2: 0, are again

circles,

so this is a

surface

revolution

aboutthe

z-axis.

Thetracein the

xz-plane

is the part of the linez = 2xwithz 2:

general,

thez co-

ordinate

of a pointonthe

surface

is twicethe

distance

from

the

z-axis.

The

surface

is thecone

Figure

34.4.

The

following

surface

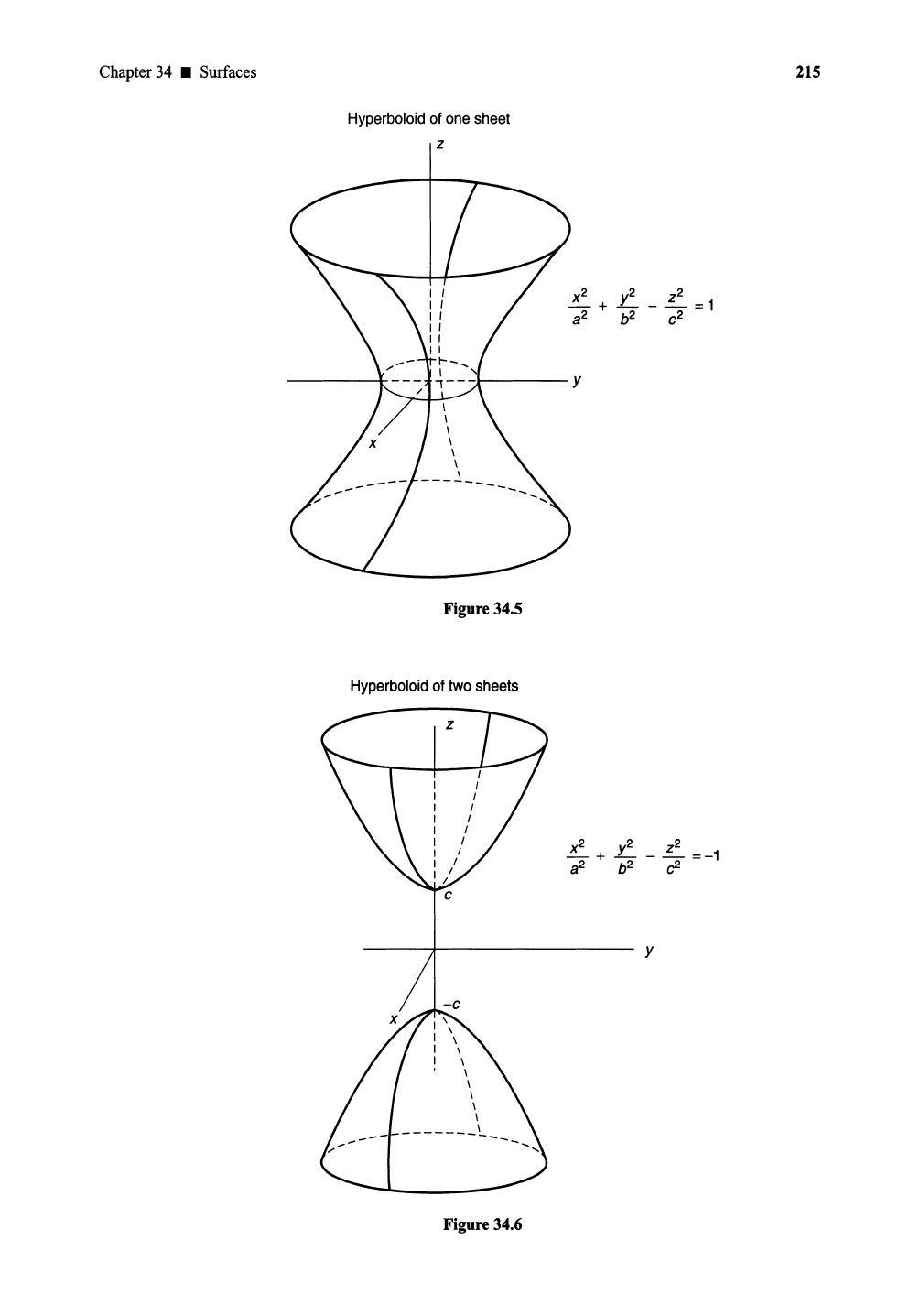
is calleda hyperboloid of one sheet

(Figure

34.5)

r Z2

-+---=1.

In eachplanez = k,the cross

section

is the ellipse

Ji2

- + - = 1

+-.

When

z =0 wegetthe ellipse

(34.5)

andwhenz = ±c,the cross

section

is the larger

ellipse,

-+-=1

with semi-axis

V2a

and

V2b

instead

and

b.The trace in the yz-plane (x = 0) is the hy-

perbola

Cone

~X2+

----~---------y

Figure 34.4

Chapter34 • Surfaces

Hyperboloid

of one sheet

t------y

Figure 34.5

Hyperboloid

of two sheets

215

Figure 34.6

216

Understanding Calculus

andthe

trace

inthe

xz-plane

(y = 0)is the

hyperbola

xl Z2

---=1.

The

graph

is the hyperboloid oftwosheets

shown

Figure

34.6.

The

surface

intersects

the

planes

for

Iki

;?; C, in the

ellipses

andthe

traces

in the

xz-plane

and

yz-plane

are

again

hyperbolas.

If a = b,the

figure

is a sur-

face

revolution.

PROBLEMS

Graphthe part of the following planesin the first octant.

34.1 The planex +2y +2z = 4.

34.2 The plane

2x+Y +4z - 8 = 0.

34.3 The planethroughthe line

x +y = 2 andthe point (0, 0, 1).

34.4 Theplane throughthe points (4, 1,0), (0, 5, 0) and (0, 0, 4).

34.5 The planex + 2y

= 4. (Thisplane is a cylindrical surface.)

Graphthe cylindrical surfaces.

34.6

= 9.

34.7

r+z2=

34.8 x = Z2.

34.9 x

+ (z - 1)2= 1.

34.10 x =

V"Y.

Findthe centerand radiusof the spheres.

34.11 x

+z2 - 2z = 3.

34.12 x

+r +Z2 - 4x + 2y - 6z = 11.

34.13 x

+3x +r +y +Z2

=~.

34.14 x

+Z2 - 2x+4y - 8z = -17.

34.15 (a) What is the highestpoint (i.e.,biggestz) on the sphere

+r +Z2 - 2x +4y -

+ 17=

(b) Describe the set wherethe sphereintersectsthe

xz-plane.

Graphthe

following

surfaces.

34.16 x

+ Z2 = 4.

34.17 x

+ z2 = y.

34.18 r + r

=z2.

34.19 z = 3(x

+r).

34.20 x

-z2

= 1.

34.21

r +Z2 = 1.

34.22 r + Z2 - r =

-1.

34.23 f + 1+

= 1.

Partial

Derivatives

Suppose

z = fix, y) is a

function

of the two

independent

variables

x andy. Ifwe fix oneof the

variables,

sayy, thenz

becomes

function

of the

single

variable

x, and we can

calculate

the

derivative

of z withrespect to x in the usual

way.

This

derivative,

the partial derivative of z

with respect to x, is

denoted

The curly-d is used to

indicate

that the other

variables

are

fixed.

Alternative

notations for the partial

derivative

withrespect tox are

f(x,

y) =

h(x,

y).

The

formal

definition of

= +( ) =

f(x

ax,y)

f(x,y)

...

x,y

lD1

A,.

•

Ax--+O

aA.

Thepartial

derivative

ofz withrespect toy is defined

similarly:

f(x,

y +

ay)

f(x,

=/(x,y)=hm

A •

Y dy--+O

Notice

that : and

areagain

functions

ofbothx andy.

Hereare some

sample

computations.

Iff(x,

y) =x

+ xy + 3

5, then

!x(x, y) = 2x+y,

!;(x,y)=x+

Iff(x,

y) =

xy2ex,

then

h(x,

y) =rex+ xy'e',

!;(x,

y) =

2xyex.

217

218

Understanding

Calculus

If z =x sin(x

+y), then

- = sin(x

+y) +

x(cos(x

y»2x,

- =x

cos(x

+y).

If z = xe", then

If there are three or more independentvariables, say u

=f(x, y, z), then u has a partial

derivative with respectto each of its independent variables. The notation is

au au au

fx(x,

y, z),

J;,(x,

y, z),

=!z(x,y, z).

For example,if

u =x

+yz+ sin y,

then

ax =

2xyeZ,

- =x

+2yz +2y

cosy,

- =x

+y.

The partial derivatives

fx(x,

y) and

J;,(x,

y) are functions of two variables, so they also

havepartial derivates. The functionj

(»,y) has the twopartialsfxx(x, y) andfxy(x, y). The func-

tion.!;(x,

y) similarlyhas two partials,.!;x(x, y)

andf>y(x,

y). If z =f(x, y), then these second

partials are indicatedwith the curly-dnotationas

follows:

az)

tflz

fxx(x,

y),

az)

tflz

ay ax

ayax

fxy(x,

y),

az)

tflz

ax ay

axay

J;,x(x,

y),

az)

dlz

- - = - =

(x y).

ay ay

ay2

>y'

For example, if

z =x

sin(xy),

(35.1)

Chapter35 • Partial

Derivatives

then

- =2xe

cos(xy),

a'lz

-2

2eY

- r

sin(xy),

a'lz

2xeY

cos(xy)

-xy

sin(xy).

ayax

219

(35.2)

The four

second

partials are

nominally

fourdistinct

functions,

but it turns out that the

two

mixed

partials,

andt:x,

arethe

same.

checkthis for the

function

(35.1)

above:

z =x

+sin(xy),

- =x

2eY

cos(xy),

a'lz

- =

2xeY

cos(xy)

-xy

sin(xy).

(35.3)

axay

Equations

(35.2)

and

(35.3)

arethetwo

mixed

partials, andtheyare

equal.

If the

mixed

second

partials are

continuous

(andtheyare forthe

common

functions

calculus),

then

t:x,

andthereare onlythreedistinct

second

partials.

EXAMPLE

35.1

Calculate

::,

t:x.

and

andverifythat the mixedsecondpartialsare equalif

y +

xy2

e",

Solution

ax =3x

y +

yeX

Jlz

= 3x

21J

xyeXY

ayax

'J ,

+ 2xy +

xeX

iPz

= 3x

+2y +

xyeXY.

axay

Themixedsecondpartialsare thesame,so theorderof differentiation doesn't

matter.

Thisis also

true forhigherorderpartial

derivatives.

For

example,

if youdifferentiate z withrespectto x, theny, then

x againyougetthe same

function

as if youdifferentiate withrespecttox twice,andthenwithrespectto

y, or if youfirst differentiate withrespecttoy, thendifferentiate twicewithrespecttox. In

symbols,

fxyx(x,

y) =

~xx(x,

y) =

fxxy(x,

y).

EXAMPLE

35.2

Show

thatfxxy(x,

andfxyx(x,

y) are the same forf(x, y) =

xy2

yeX.

Solution

f(x,

y) =

xy2

+yeX,

fx(x,y) =

yeX,

220

Understanding Calculus

fxx(x,

y) =

y~,

fxxy(x,y)

=~,

fxy(x,

y) = 2y + e,

fxyx(x,

y) =

ex.

Thus

!xyx(x,

y) = f

xxy(x,

y) =

ex.

PROBLEMS

and

aye

az az

and

aye

iPz

aiL·

az az

and

aye

iPz

axay

and

ayax·

u = se-

35.8 z = sin

cos 6

35.2 z = xy

sin(xy)

35.3 z = sec(x+y)

35.4 z = extan(x +2y)

35.5 z = x

y +

3xy2

35 6

~2+y2

iPz

aiL.

35.7 z =

,-2(1

- cos 6)

Findthe indicatedpartial

derivatives.

35.1 z = x

y +sin(x

+I)

35.9 V=

TTr2h

35.10 S = 5

Wp2

ar and

aB·

iPz

aer·

d ev

arr·

as as

and at·

iPu

and "Jj2.

au au

35.12 u = tan5 ar and

ao·

Check that the given mixed partials are the same for the following functions.

35.13 f(x, y, z) = x

+y3 +xz ; f

andfzxx.

35.14 f(x, y, z) =

+y2 ; f

andfzyy.

35.15 f(x, y, z) = x sin(yz) ;

J;,xz

andfxyz.

35.16 f(x, y, z) = x

cosZ

xxy

and

fxyx.

Showthat the

following

functions u(x,y) satisfyLaplace's equation

Uxx

+ u

35.17

u=x

-1.

35.18 U = 2xy.

35.19

U = x

3xy2.

35.20 U = excosy.

35.21 U = log(x

+I).

35.22 U = tarr'

35.11

Showthat the

following

functions satisfythe heat equation

Uxx

= u

35.23 U = e:'sinx.

35.24 u =

e--4t

cos 2x.

35.25 u =

coshax.

35.26

U = x

+ 2t.

35.27 U =

+ 12x

t +

12t2.

35.28 U =

•

Tangent

Plane

and

Differential Approximation

The partial

derivative

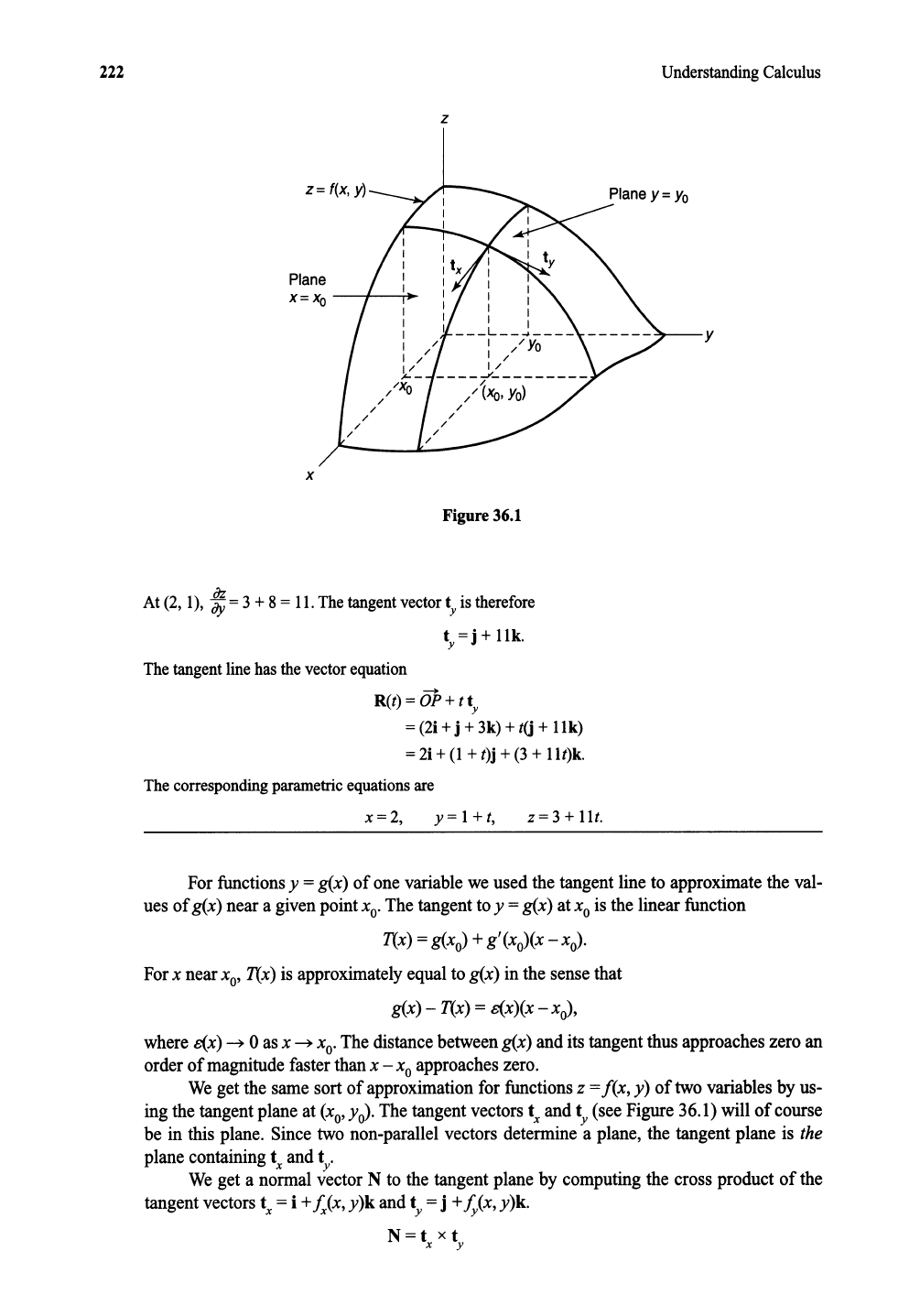
!x(x, y) represents the slopeof a certaincurvein the samewaythat the

one-variable

derivative

(x)

does.

The graph of z =

!(x,

y) is a surfacein three-space. If we

fix one variable, say

y =

Yo,

thenwe determine the curvewherethe planey =

intersects the

surface

z =f(x, y).

(Figure

36.1).

Thex-partial,!x(x,

Yo)

is the slopeof this curve,i.e.,the tan-

gent of the anglethe tangentline makeswiththe

xy-plane.

A tangent vector to the curve z = f(x,

Yo)

at a point (x

yo,f(x

Yo))

=i +!x(x

yo)k.

There is no j-componentin the vectort

since it lies in the planey =

whichis parallelto

the

xz-plane.

The

derivative

!;(x

y) is the slope of the curve wherethe plane x = X

intersects the

surface

z =f(x, y). A tangentvectorto this curveat (x

yo,!(x

Yo)

=j +!;(x

yo)k.

EXAMPLE 36.1

On the curve where the plane x = 2 intersects the surface z =

2xy2

- 2 find the tangent vector t at P

= (2, 1, 3). Write the vector equation

the tangent line to the curve at (2, 1, 3), and write the corre-

sponding parametric equations for the line.

Solution

Sincex is

constant

onthe

curve,

the

tangent

linewillhaveslope

atx = 2,y = I.

calculate

=31+4xy.

221

222

Understanding

Calculus

Plane

x=xo

Figure

36.1

At (2, 1),

= 3 +8 = 11.Thetangentvectort

is therefore

= j + 11k.

Thetangentlinehas the vectorequation

R(t)

=OP+

= (2i + j +3k) +t(j + 11k)

= 2i +(1 +t)j +(3 + 11t)k.

Thecorresponding parametric

equations

are

1 +t,

z = 3 +

lIt.

For

functions

y =g(x) of one variable we used the tangentline to approximate the val-

ues of

g(x) near a givenpointx

Thetangenttoy =g(x) at X

is the linearfunction

T(x)=g(x

+g'

(xo)(x

- x

o)'

Forx nearx

T(x) is approximately equalto g(x) in the sensethat

g(x) - T(x) = e(x)(x

-x

o)'

wheree(x)

0 asx

The distance betweeng(x)and its tangentthusapproaches zero an

orderof magnitude fasterthanx -

approaches zero.

get the same sort of approximation for functions z =

f(x,

y) of two variables by us-

ing the tangentplane at

Yo)'

The tangentvectors t

and t

(seeFigure36.1)will of course

be in this plane. Since two non-parallel vectors determine a plane, the tangentplane is

the

planecontaining t

andt

get a normal vectorN to the tangentplane by computing the cross product of the

tangentvectors

=i +

!x(x,

y)k

andt

=j +

!;(x,

y)k.

N=t

x t

x y

Chapter36 •

Tangent

Planeand Differential Approximation

j k

1 0 fx(x

Yo)

o 1 1;(x

Yo)

=-fx(x

yo)i- f;(x

yo)j+ k.

Hence the tangent plane to z = f(x, y) at (x

Yo,

zo)has the equation

-fx(x

yo)(x- x

- f;(x

Yo)(Y

Yo)

+(z-

zo)

= 0,

223

(36.1)

(36.2)

EXAMPLE

36.2

Findthe equationof the plane tangentto the surfacez = 2.ry+

- x at (1, 3).

Solution

Wefirst calculatej'jl, 3) and1;(I, 3).

fx(x,y)

=4xy - 1 ; fx(l, 3) = 11;

1;(x,y)

=2x

; 1;(1, 3) =29.

Sincef(l, 3)

= Zo = 32, the equationof the tangentplane is

z = 32 + 11(x - 1)+29(y- 3).

If z

= T(x,y) is the tangentplane (36.2), then the error betweenf(x, y) and T(x,y) is limitedby

the inequality

If(x,y) -

T(x,y)1

S e(x,y)

-xol+

Yol],

where e(x, y)

0 as (x, y)

Yo).

The error betweenthe function values and the tangentplane is

again an order of magnitude smallerthan the distancefrom

(x, y) to (x

Yo).

We can expressthis ap-

proximation as

follows:

(36.3)

For

and

small,the right side gives a good approximation tof(x

ax,

~y)

in terms of the

values

off

and its derivatives at (x

Yo).

EXAMPLE

36.3

Use the tangent plane approximation (36.3) to find the approximate value

off

(x, y) = x

e.v

+ cos y at

(0.9,0.2).

Solution

Wecan easilycomputef(x,y) and its partialsat (1,0), whichis near (0.9,0.2).

1,0) = 1

•

+ cos 0 =2;

fx(x,y)

=3x

;

fx(l, 0) =3;

1;(x,y) = x

siny ; 1;(1,0) = 1.

Nowuse

=-0.1 and

=0.2:

f(.9, .2) =

f(l,

0) +3(-0.1) + 1(0.2)=

2 - 0.3 + 0.2 = 1.9.

The calculatorgivesf(0.9, 0.2)

= 1.87,so our quickapproximation is off by only .03.