Bear H.S. Understanding Calculus

Подождите немного. Документ загружается.

246

Understanding Calculus

z =

f(x

, y)

+---y

llA

Figure 40.1

(40.2)

valueof x in [a, b], and calculate the area of the cross-section of solid

where

the planex =

constant intersects the

solid.

IfA(x) is this

area,

then

A(x) = r

f(x

,y)dy.

Nowthinkof

slicing

the

volume

intothinslicesof widthdx,

where

theareaof the sliceatx is

A(x). The

volume

of sucha sliceis dV = A(x)dx.

addup (integrate) all these

volumes

asx

runsfroma to b to getthetotal

volume

v = t A(x)dx =

t(rf(X,

y)dY)dx.

+--'---1--

Figure 40.2

(40.3)

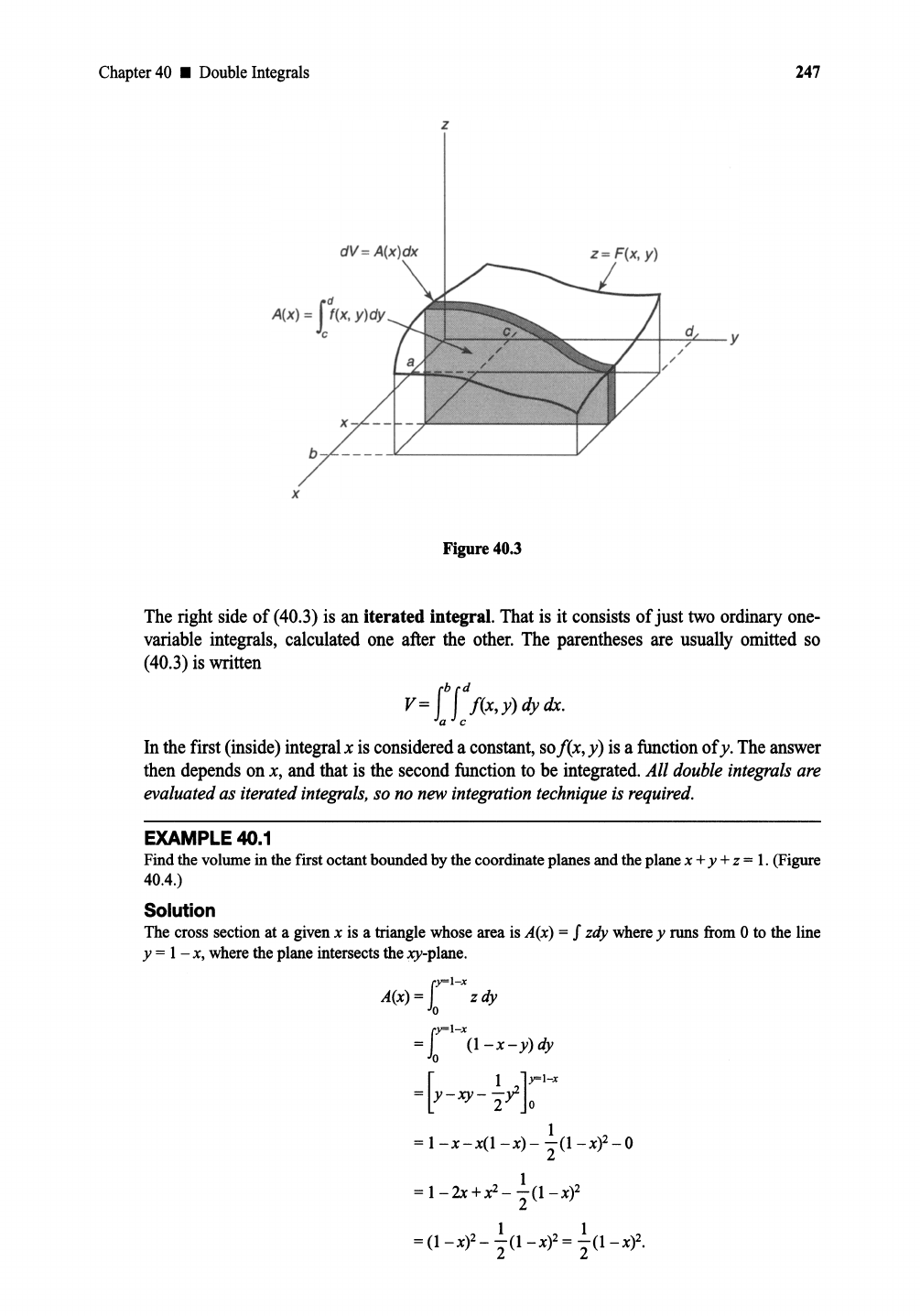
Chapter 40 • Double Integrals

=A(x)dx

Figure

40.3

Z = F(x , y)

247

The right side of

(40.3)

is an

iterated

integral.

That is it

consists

ofjust

two

ordinary

one-

variable

integrals,

calculated one after the

other.

The

parentheses

are

usually

omitted

(40.3)

is written

ttf(x,y)dydx.

a c

In thefirst

(inside)

integral

x isconsidered a

constant,

sof(x, y) isa

function

ofy.The

answer

then

depends

onx, and that is the

second

function

to be

integrated.

All

double

integrals

are

evaluated as iterated

integrals,

so no new

integration

technique

required

EXAMPLE

40.1

Find the volume in the first octant bounded by the coordinate planes and the plane x +y +z =1. (Figure

40.4.)

Solution

The cross section at a given x is a triangle whose area is A(x) =I zdy where y runs from 0 to the line

y = 1 - x, where the plane intersects the xy-plane.

l-X

A(x)=

0 z dy

l-X

(l-x-y)dy

[

]r=I-X

y-XY-"2

= I

-x-x(l-x)

_(l-X)2

- 0

1-2x+r-

-(I-xf

I I

=(I-X)2

"2(I-x

= "2(I-x)2.

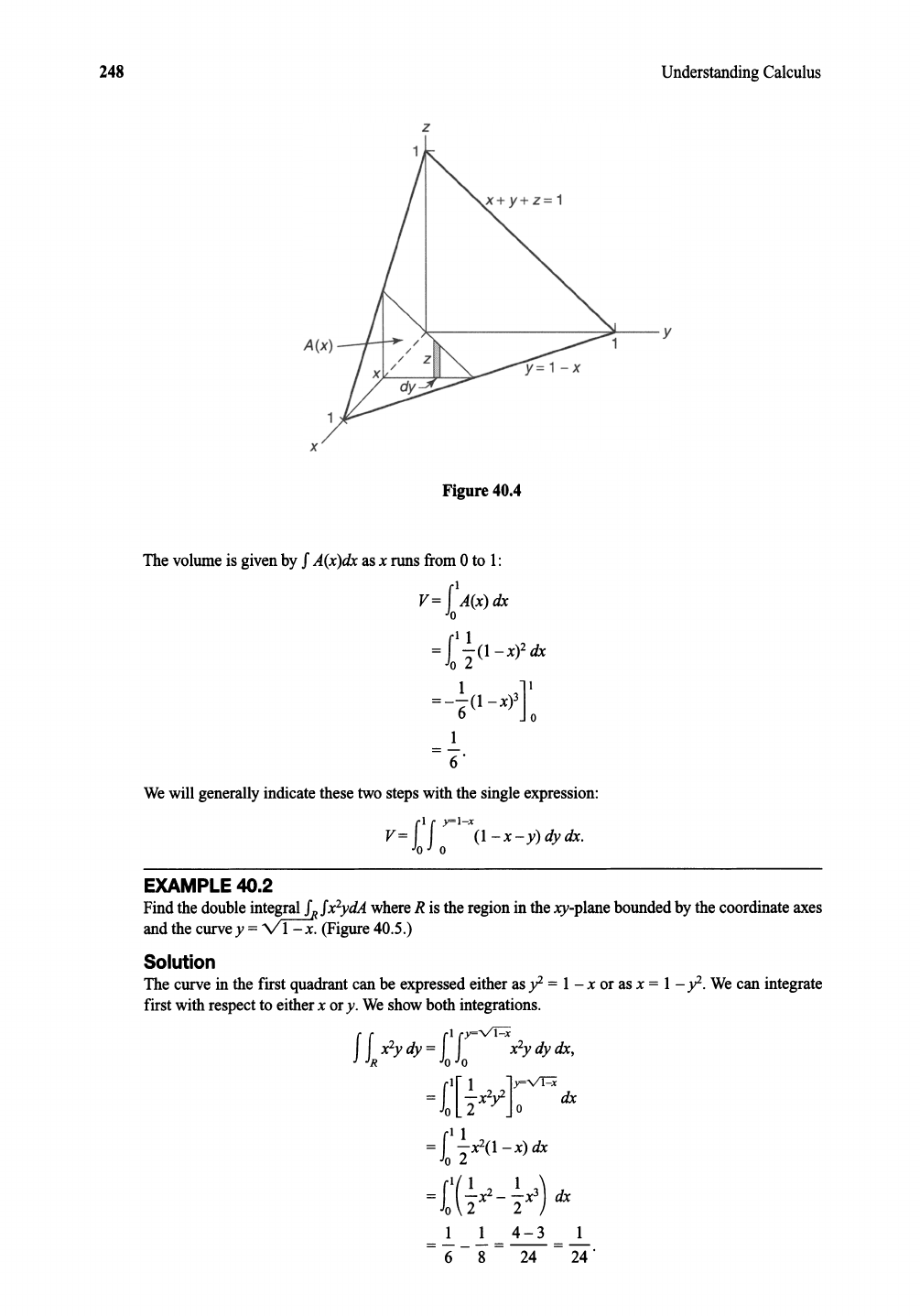
248

Understanding Calculus

A(x)--I-t"-"""""

~-----------:,ilJ---y

Figure 40.4

The

volume

is givenby JA(x)dxas x runs from0 to 1:

fA(X)dx

i 1

-(l-x}2dx

o 2

1 ] 1

=--(1-x)3

6 0

6 '

Wewillgenerally indicate thesetwostepswiththe singleexpression:

rl-x

0 0

(l-x-y)dydx

EXAMPLE

40.2

Findthe

double

inte~

rydA

whereR is the regionin the

xy-plane

bounded by the coordinate axes

andthe

curvey=Vl-x.

(Figure

40.5.)

Solution

The curve in the first quadrant can be expressed either as y = 1- x or as x = 1- y .Wecan integrate

first withrespectto eitherx ory. Weshowboth integrations.

rydy=

fI:vr=x

rydydx,

faT

]~VT=X

~r(l-x)

o 2

)

1 1

4-3

8=24=

24 '

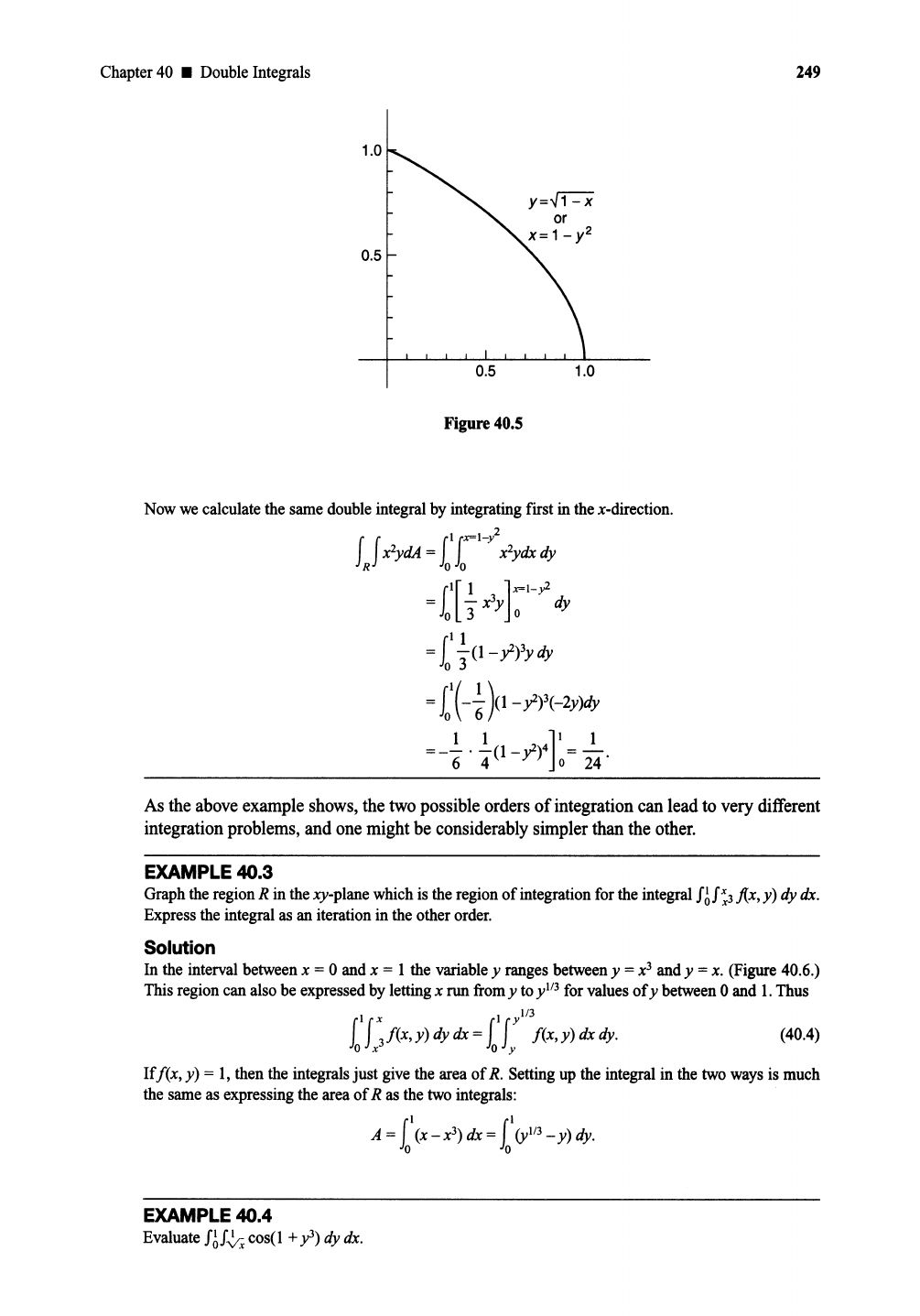
Chapter40 • DoubleIntegrals

249

1.0

0.5

0.5 1.0

Figure 40.5

Nowwecalculatethe samedoubleintegralby integrating first in thex-direction.

x=I-

ffrYdA=II

rydxdy

ROO

I[ 1

]X=l-r

= - x

030

I I

-(1

-1)3

o 3

-i

)(1-

y)3(-2y)dy

1 1 ] 1 1

=--

-(1-1)4

6 4 0

24·

As the

above

example

shows,

the twopossible ordersof integration can leadto very different

integration problems, and onemightbe considerably simplerthan the

other.

EXAMPLE 40.3

Graphthe regionR in the

xy-plane

whichis the regionof integration for the integral

fAf~3

f(x, y) dy dx.

Expressthe integralas an iterationin the other

order.

Solution

In the interval betweenx = 0 and x = 1 the variable y ranges betweeny =x

andy =x.

(Figure

40.6.)

Thisregioncan also be expressed by letting

x run fromy to yl/3for valuesofy between0 and 1.Thus

1 1 1/3

f:f(x,y)dydx=

I r

f(x,y)dxdy.

(40.4)

o x 0 y

If!(x, y) = 1, then the integralsjust givethe area of R. Settingup the integralin the two waysis much

the sameas expressing the areaof

R as the twointegrals:

A =f(x

-x

) dx =

f(y1l3

-y) dy.

o 0

EXAMPLE 40.4

Evaluate

fAf~

cos(1

+ y3)dy dx.

250

1.0

0.8

0.6

0.4

0.2

Understanding

Calculus

(1, 1)

-~~"""=---'-_--l..

.l...-_-'--x

0.2 0.4 0.6 0.8 1.0

Figure 40.6

Solution

Inthe form

presented,

weare

faced

withthe

impossible

integral

cos(1

+I)

dy.

Ouronlyhopeis that

the integration in the other orderwill be more

tractable

. The

region

of integration is the area

between

the curvey =

v'.X

andy = I, for 0 s x s 1.

(Figure

40.7.)

rewrite

the

integral

withthe iteration in

theotherorder:

I I I

x=i

cos(l +

dy dx=i f cos(l +

dxdy

Jx=a

=f(cos(l +

l)x

]~2)

=f[cos(l +

I)y]

I ] I I 1

sin(1

0 =

sin2 -

sin 1.

-.-.

..(1

,1)

Figure 40.7

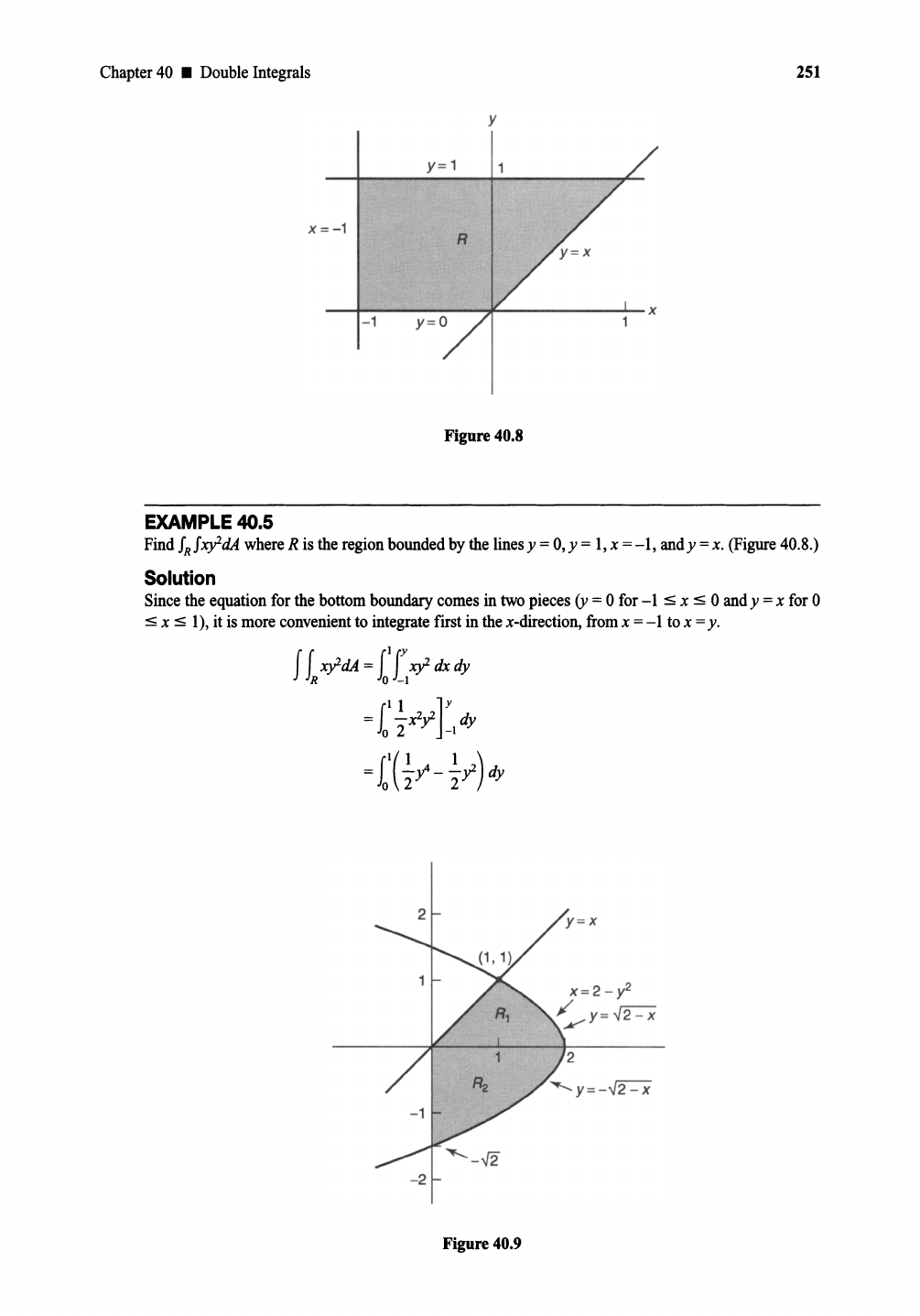
Chapter

40 •

Double

Integrals

- 1

Figure 40.8

251

EXAMPLE

40.5

Find

fRfxldA

where

R is the

region

bounded

bythe linesy = O,y = 1,x

=-1,

andy =x.

(Figure

40.8.)

Solution

Sincethe

equation

for the

bottom

boundary

comes

in twopieces(y =0 for-1 S x S 0 andy =x for0

S x S I), it is more

convenient

integrate

first in the

x-direction,

from

x =- I tox =y.

xldA

=fr

dx dy

R 0

-I

- 2

Figure 40.9

252 Understanding Calculus

5 !

! _

-4

_ 2-

- lOY - 6

0 - 10 - 6 - 60

--15'

EXAMPLE

40.6

Find ffR(1 +y)dA where R is the larger region boundedby the y-axis, the line y = x, and the curve

x = 2 -

y2.

(Figure

40.9.)

Solution

No matter whether we integrate first in the x-direction, or first in the y-direction, there are going

to have to be two integrals, because both the top boundary and the left boundary are given in two

pieces. If we integrate from left to right first we have the right hand boundary

x = 2 -

y2.

If we inte-

grate from downto up first we will havethe two boundarys

y = ±V2=X.

Polynomials

are easierthan

radicals, so we will integrate in the x-direction first, with separate integrals for

and R

(see Figure

40.9).

ff (1 +y)dA =f

r=2-

(1 +y)

the

0 x=y

= f(x +yx)

t:-?

= f([2 - Y+y(2 -

y)]

- [y +y]) dy

L\2

- Y+ 2y - Y - y - y) dy

L\2

- 2y+Y - y) dy

Y-

Y +

!y_

!y"]l

3 2 4 0

2 1 1 24 - 8 + 6 - 3 19

=2-3"+"2-"4=

=12'

Forthe lowerregionR

wehave

f f (1 +y)dA = r

r=2-

(1 +y)

the

-Y2

x=0

o ]X=2-y2

(x+yx)

-Y2

x=O

=r[2 - Y+y(2 -

y)]

-Y2

=r(2 + 2y - Y-y) dy

-V2

1 1 ] 0

= 2y - _y3 +

_ _ y4

4-V2

-2V2

+ +(2V2) + 2- 1]

2 4

=2V2-

3"V2+

1= 3

+ 1.

The final resultis

Chapter40 • DoubleIntegrals

(1+

y)dA = I

+ I

R R} R

19 4

=-+I+-V2

12 3

31 4

=U+"3

V2·

PROBLEMS

253

Evaluate the iteratedintegral. Graphthe regionof integration in the

xy-plane.

Calculate the same

integral by integrating in the opposite order, with the appropriate new limits. (The

answers

shouldbe the same.)

40.1

fJf~

+y) dy

dx.

40.2

fJf~xy

dx.

40.3

fJf

+y) dy

dx.

40.4

f~f~{

(2 +y) dxdy.

40.5

f~f~

xy2

dx.

Evaluate the

following

doubleintegrals.

40.6 fRfx2ydA, R = {(x,y): °S Y S x, os x S I}.

40.7 f

Rf(x

2)dA,

R is the regionbetweeny =X

ll2

andy

1l3,

°S X S 1.

40.8

fRfeY2dA,R={(x,y):osxS2y,OSyS

I}.

40.9

fRfyeXdA,

R = {(x,y) : °S x S

os y S I}.

40.10 fRf 2ydA,R is the regionboundedby the axesand the linesx + y = 1,x + y = 2.

40.11 Use symmetry arguments to show that the

following

integral is zero: f

Rfx(1

y)dA,

whereR is boundedbelowbyy =-1 +

Ixl

and abovebyy =

Line Integrals

As we saw in an earlier chapter, work is defined as force times distance. Specifically, the

work done by a constant force F acting along the segmentfrom a to b is F x (b - a). If the

force is not constant,sayF = F(x),then the workdone in movingfroma to b is

tF(x)

dx.

(41.1)

Now supposea particle movesalong the segmentfrom (xl' Yl) to (x

)

in the plane,

and a constantforce F

= ai +bj acts on the particle at every point of the segment. The work

done is again forcetimes distance,but now "force" meansthe component

ofF

along the seg-

ment.The vector from (xl' Y

)

to (x

)

is V = (x

Xl) i +

(Y2

- Y

)

j, and the component of

F along V is

IIFIlcos

8, where 8 is the angle between F and V. The force acts through a dis-

tance

IIVII,

<IlFllcos

IIVII

= F .

Supposethe forceis not constant,

(41.2)

F(x,y) =P(x, y) i + Q(x, y) j,

and the path is a curve C ratherthan a segment. Toevaluatethe workdoneby F movingalong

C we dividethe curveup into small pieces with points

(Xi'

on the curve. Let

- X

and aY

- Y

•

Then

i + aY

is the vector from

(Xi-I'

Yi-l) to

(Xi'

y).

Ifax

and aY

are small,

is closeto the curve, and

the workdone by F going from

(Xi-I'

Yi-l) to

(Xi'

is approximately

F(xi,y)·

=(Ptx;

i + Q(x

. (ax

i +

~Yi

=Pix;

y)ax

+ Q(x

y)aY

(41.3)

2SS

256

Understanding Calculus

The

actual

work

done

by F

moving

along

Cis the

limit

ofthe

sums

~~~

as all Sx, and

~Yi

approach

zero:

W= limI

F(xi,y)·

~Si

= limI Pix; y)Llx

+Q(x

Y)~Yr

Thislimitis calleda line integral and is denoted

fl' ds = !cP(X,y) dx+ Q(x,y) dy.

If C is parameterized by the equations

(41.4)

x =

I(t)

y = g(t),

a -s t :s; b,

thenthe line integral

(41.4)

evaluated

by substitutingj(r) forx, g(t) fory, andreplacing the

differentials

dxanddy byI'(t)dt,g'

(t)dt.

Theresulting expression is integrated overthe range

of the parameter; i.e., from

a to b, so

F·

ds =LP(x,y) dx+ Q(x,y) dy

c c

=t[P(f(t),

g(t»f'(t)

+Q(f(t), g(t»g'(t)] dt.

EXAMPLE

41.1

Let F(x,y) = (x + 1)i + 2xy j, and let Cbe the curvex = t

2,y

= 2t, 0

t -s 1.Find

fcF·

ds.

Solution

(F'ds=

l(x+l)dx+(2xy)dy

= f[(P+ l)2t + 2p(2t)2] dt

= f[2t

+ 2t+

8t3]

~t4+P+2t4]:

(41.5)

EXAMPLE

41.2

A particlemovesthroughthe forcefield F(x, y) = (x

i + xy j alongthe top half of the unit circle,

from(1, 0) to (-1, 0). Findthe workdone.

Solution

The workis givenby

(F'ds=

i(x

2+y2)dx+.xydy.

The curve is conveniently parameterized by

x = cos

(J,

y = sin

(J,

0 -s (J-s 71'.

The line integral, with dx =-sin (Jd(Jand dy =cos (Jd

(J,

becomes