Bhattacharjee J.K., Bhattacharyya S. Non-Linear Dynamics Near and Far from Equilibrium

Подождите немного. Документ загружается.

Preface

Non linear dynamics has been almost synonymous with the dynamics of a few

degrees of freedom. This is somewhat extra-ordinary given the fact that natural

phenomena are most often described by partial differentialequationswhichhavean

inﬁnite number of degrees of freedom and more often than not the relevant partial

differential equations are nonlinear. We thought that, for a change, it would be

worthwhile to focus on the continuous systems and describe some of the nonlinear

phenomena that have captured the attention of researchers over the last ﬁfty years.

Interestingly enough for these systems with inﬁnite degrees of freedom, it is real

life experiments (as opposed to computer simulations) that are more common

and this allows one to confront theoretical ﬁndings with laboratory experiments.

Calculations use idealised phenomenological models which have a fair amount of

approximation and try their best to describe the complex phenomena of the real

world and it is quite exhilarating when the calculations and observations match.

The theoretical analysis can proceed along two different routes-analytical and

computational. In this book, we have tried to bring together some of the analytical

tools which have been successful in producing results for systems which are close

to equilibrium as well as for those that are far from it. We hope the beginning

graduate students who want to take up the study of statistical physics will ﬁnd it

useful.

We are deeply indebted to Mr. J.K. Jain of Hindusthan Book Agency for

his tremendous patience and his willingness to help at evey stage. It was Prof

R. Ramaswamy of JNU, New Delhi who ﬁrst suggested that this could be done.

But for him, the project would not have been initiated. We would like to thank

Sagar Chakrabarty of SN Bose Centre, Kolkata, for his university help with the

ﬁnal proof reading.

Introduction

We will be concerned mainly with systems with inﬁnite degrees of freedom which

can however, be described by a few variables. These variables must necessarily

be ﬁelds i.e. functions of space and time. A typical example would be to try to

describe the ﬂow of air around us. The variables that would be necessary to describe

the state of air would certainly be its density, its temperature and its velocity. All

these variables (density, temperature and velocity) are, in general, functions of

space and time. They are mesoscopic variables. They do not reﬂect the variations

occurring at the molecular level. To deﬁne a density, it should be recalled, we take

a small volume (small compared to the total system size, yet large compared to

atomic dimensions) and consider the mass of this small volume. The ratio of mass

to volume remains constant for a reasonably large variationin the size of the volume

chosen and deﬁnes the density of the system. It fails to be a constant if the volume

becomes so small that it contains only a few molecules. In that case our description

in terms of a density fails. All the systems that we will talk about can be described

in terms of a coarse grained ﬁeld like the density. Because of the smallness (at

the macroscopic level) of the volume used in deﬁning density it can be considered

a local variable. This is what makes it a ﬁeld. Similarly we can talk about the

local temperature and local velocity. The local velocity is not the velocity of an

individual molecule but the velocity associated with a macroscopically small, yet

microscopically largevolumeof air. These ﬁelds evolvein time and space according

to some deﬁnite laws. Every separate system that we discuss will have its own rule

for evolution. All these systems have attracted a vast amount of attention for several

decades. A lot of spectacular progress has been made and a lot more remains to be

understood. Our aim in this book will be to describe a few analytic techniques which

have been very effective in providing some sort of common platform for widely

varying problems of dynamics. While often the eventual detailed understanding

2 1 Introduction

of these systems require extensive numerical work, some of the essential features

can often be captured by these analytic techniques. The confrontation between

calculations and real life experiments in such cases provides a good measure of the

worth of the theory. In this introductory chapter, our focus will be on providing a

glimpse of some of the more interesting comparisons of theory and experiment in

one of the systems we wish to study - the second order phase transitions.

The thing to stress, as the theme of this book, is the common platform of theo-

retical techniques suited for diverse problems - ‘universal’ techniques to borrow a

much used word. Universal was the key word that triggered a tremendous amount

of interest in critical phenomena in the nineteen sixties and seventies. Critical phe-

nomena exhibited universality and hence it was worth the effort spent to get to the

bottom of it. We will begin by explaining what universality meant in that context.

The two most common second order phase transitions or critical phenomena

are the paramagnet to ferromagnet transition at the Curie point and the gas liquid

transition at the critical point. These are second order transitions since they require

no latent heat.

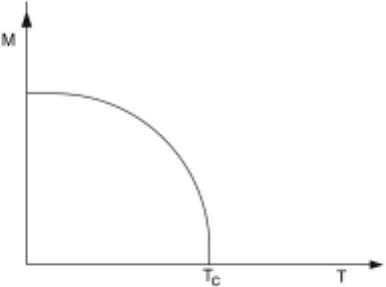
If a material like iron is taken and kept at a temperature signiﬁcantly higher

than the room temperature (but lower than its melting point, needless to say) then

it will not show any spontaneous magnetization. Spontaneous magnetization is the

magnetization that one obtains in the absence of any external ﬁeld. Experimentally

it is determined by switching on a small external ﬁeld, ﬁnding the magnetization

at different values of the ﬁeld and taking the limit of the external ﬁeld going to

zero. If we cool the piece of iron, then at a certain temperature T

, the critical

temperature or the Curie temperature, the system undergoes a phase transition. For

temperatures above the critical temperature T

the spontaneous magnetization is

zero, while below T

the iron exhibits non-zero spontaneous magnetization. The

magnitude of the magnetization rises automatically from its value of zero at T

the temperature is lowered. A typical measurement yields the kind of behaviour

shown in Fig. 1.1.

It is the region very close to T

which is interesting. Here the magnetization

has the behaviour

M ∝(T

−T)

for

−T

1 (1.0.1)

The quantity β is called a critical exponent and for this magnetic transition, β

is independent of what material one is using for the experiments. It could be a

transition metal like iron, nickel or manganese, or it could be a rare earth compound

like EuO or EuS. For different materials the actual values of magnetization are

different but the exponent β remains the same. This is universality.

Large ﬂuctuations characterize the critical point. This can be seen from a study

of the linear response functions. In the case of the magnet the response function is

the zero ﬁeld susceptibility. One applies an inﬁnitesimal ﬁeld H and determines the

corresponding magnetization M. The isothermal susceptibility is deﬁned as χ

∂M

∂H

)

. It is the zero external ﬁeld that concerns us. Whether for T>T

or T<T

1 Introduction 3

Figure 1.1. Spontaneous magnetisation as a function of temperature

the susceptibility becomes very big as one approaches T

, and this behaviour, which

culminates in the susceptibility diverging at T =T

, can be represented as

∝|T −T

−γ

(1.0.2)

Once again, the exponent γ is independent of what material was used to study the

phase transition. The strong response of the system comes from the fact that near

, the ﬂuctuations are very big. An inﬁnitesimal change in temperature around T

changes the system from a disordered to an ordered state. As the critical tempera-

ture is approached blobs of ordered phase start appearing in the disordered region

and gradually these blobs become correlated as the temperature is further lowered

to the critical point. This makes the system very susceptible to small perturba-

tions. At a temperature inﬁnitesimally close to T

, switching on an inﬁnitesimal

ﬁeld can produce a ﬁnite amount of magnetization in the system. This is why the

susceptibility (isothermal) diverges at the critical point.

It should be clear from the above discussion that the description of the phase

transition should be couched in terms of a local magnetization, the magnetization

of the blob of the ordered phase that appears in the disordered system. This blob is

like the ‘small’ volume that is used in deﬁning density. It is small in comparison to

the system size but it is large enough to wash out the individual effects of the atomic

magnetic moments. This local magnetization is a function of space (and also time

in general) and can be described by a ﬁeld φ(r,t). The ﬁeld is usually a vector

ﬁeld in the case of magnetization. However, there can be uniaxial magnets where

the magnetization can only be along a deﬁnite direction in space. In such situations

the ﬁeld φ(r,t) is a scalar ﬁeld. In certain planar magnets, the magnetization is

conﬁned to lie in a plane and then the ﬁeld φ(r,t) is a two-dimensional vector

ﬁeld. This brings in an even wider instance of universality.

We focus now on yet another critical point - the one discovered by Andrews in

his experiment on CO

in 1869. The experiment measured the P-V curve for a ﬁxed

4 1 Introduction

mass of CO

at different temperatures. At the lower temperatures (T

), as

the pressure is increased, the volume decreases and over a range of volume when

the vapour changes to liquid the pressure remains constant. When all the vapour

is converted to liquid, the volume decreases slightly as the pressure is further

increased.

Figure 1.2. Isotherms for a liquid gas transition

The conversion from gas to liquid occurs with the emission of latent heat. As the

temperature was increased, it was seen that the ﬂat part of the curve corresponding

to the phase transformation and eventually at T =T

, the ﬂat part disappeared

which meant that the density of the liquid and vapour had become equal at this

temperature. For T>T

, there is only a single-phase region. The transition from a

two-phase region below T

to a single-phase region above T

is a second order phase

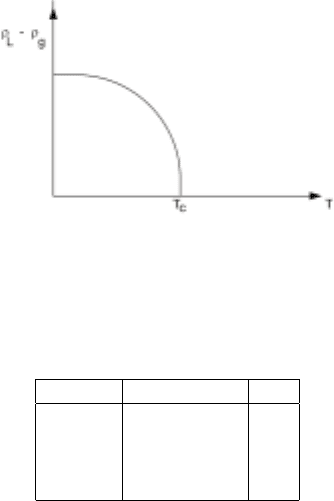
transition which occurs withoutany latent heat. If we consider thedensity difference

−ρ

, the difference between densities of liquid and vapour (gas) phase, then

it vanishes for T>T

(single-phase region) and increases with temperature for

T ≤T

. The graph of ρ

−ρ

vs. T is shown in Fig. 1.3 and is remarkably similar

to the corresponding ﬁgure for magnetization shown in Fig. 1.1. For T sufﬁciently

close to T

, once again

−ρ

∝(T

−T)

(1.0.3)

If one looks at the isothermal compressibility, which is the change of density for an

inﬁnitesimal change in pressure, then it is found that the compressibility diverges

at the critical point. Once again this is because of the large scale ﬂuctuations in the

system. Inﬁnitesimally above T

, it is a single-phase region, while inﬁnitesimally

belowit is a two-phase region. In this range, a small change in an external parameter

like the pressure can cause large changes in the density and that is what causes the

singular response

∂ρ

∂P



∝|T −T

−γ

(1.0.4)

1 Introduction 5

Figure 1.3. Density difference between the gas and liquid phases as a function of temperature

The exponents β and γ are independent of what substance is used to carry out the

experiment. A few typical results are shown below.

Substance β γ

Xe 0.0321 1.236

0.0327± 0.006 1.251

0.329 1.280

0.321± 0.006

Table 1.1 Univesality of critical exponents for the liquid gas transition.

As T approaches T

from above local blobs are formed where ρ

−ρ

acquires

nonzero value.These blobs get more and more correlated as T gets closer and closer

to T

and eventually one ends up with a globally non-zero value of ρ

−ρ

.Ifwe

denote the local value of ρ

−ρ

by φ(r,t), then φ(r,t) is a scalar function very

much like the uniaxial magnet and sure enough if one looks at the experiments

involving phase transitions in uniaxial magnets, then

β =0.32 γ 1.24. (1.0.5)

A similar phase transition without latent heat occurs in the critical mixing of some

liquids. If we take two well chosen liquids of densities ρ

and ρ

and consider a

mixture of these at concentrations C

and C

=100 −C

, then it is possible that

at high temperatures these liquids are completely miscible but at low temperatures

they become immiscible and a meniscus develops. The separation begins at a

temperature of T

and becomes more and more pronounced as the temperature is

lowered. If we consider the variable C =X

(T ) −C

, where X

(T ) is the relative

concentration of liquid number one at temperature T , then for all T>T

, C =0,

while for T<T

, C =0 and increases as T is lowered. The transition at T

requires

no latent heat and is a second order transition. If one now thinks of the concentration

C(r,t) being the ﬁeld φ, then φ is once again a scalar ﬁeld. From our previous

discussion it would appear that once again β should be near 0.32 and γ near 1.25.

6 1 Introduction

Substance β γ

Isobutyric acid+Water 0.324± 0.012 1.23±0.02

+Nitromethane 0.316± 0.008

Polystyrene+Cyclohexane 0.327± 0.008

3-methylpentane+Nitroethane 1.240±0.017

Table 1.2 Universality of critical exponents for the mixing transition in binary liquids.

The underlying message is very clear. Critical phenomena are universal to the point

that ﬂuids, magnets, binary mixtures all exhibit the same behaviour. Numbers like

β and γ are called critical exponents. The ﬁeld φ(r,t), which is identically zero

above the transition point and has a global non-zero value below T

, is called an

order parameter. The order parameter is characterized by the dimension of the

ﬁeld φ(r,t) which can be a three-dimensional vector, a planar vector or a scalar.

In general it can be thought of as a n-component ﬁeld φ

(r,t) i =1, 2, 3.....n with

n =1 for the ﬂuid, the binary liquid and the uniaxial magnet. Universality, means

that in three-dimensional space critical exponents are determined by the value of n

alone. If the dimension of the space is D, then critical exponents depend solely on

n and D. The method of tackling this problem of determining the critical exponents

has to be a general technique independent of the speciﬁc nature of the system. It

is because of this that critical phenomena had attracted a great deal of attention in

the last century.

We start by pointing out the different ways of tackling the individual problems.

We begin with the magnet. The local magnetization ﬁeld is m(r) [we are going

to consider statics now and will take the ﬁelds to be time independent]. The mag-

netization at two different points r and





will interact and produce an interaction

energy

int

=−



J(r −





)m(r)m(





(1.0.6)

For convenience we take m(r)to be a scalar function (uniaxial magnet). The energy

is lowered parallel moments if J>0. If there is an external ﬁeld H , then there is

an additional term −H



m(r)d

r and we have

E =−



J(r −





)m(r)m(





−H



m(r)d

r (1.0.7)

The strategy is to ﬁnd the statistical mechanical partition function

Z =



m(r)

−

(1.0.8)

and thence determine all the thermodynamic quantities like M, χ

etc. from the

free energy F =−k

T ln Z. The problem is simpliﬁed by writing

1 Introduction 7

int

(r)=



J(r −





)m(





(1.0.9)

and then assuming that the internal ﬁeld H

int

(r) is independent of the position

r. This is the so called mean ﬁeld approximation. This uniform H

int

can only be

caused by the net magnetization and can be taken to be proportional to it. Thus,

int

=JM, where J is a constant and we have

E =−(J M +H)



m(r)d

r (1.0.10)

At every spatial point r, the magnetization can be ±µ in the simplest situation that

one may consider (Ising model) and the partition function in Eq.(1.0.8), now yields

Z =



2 cosh

µ(J M +H)



(1.0.11)

where N is the number of spatial sites in the volume under consideration. The free

energy is

F =−k

T ln Z =−Nk

T ln



2 cosh

µ(J M +H)



(1.0.12)

The magnetization is found from −

∂F

∂H



M =µN tanh



µ(J M +H)



(1.0.13)

We note that M is extensive, while H

int

is intensive and hence J must have the

form

, which we substitute in Eq.(1.0.13) and write as

µN

=tanh





µN



. (1.0.14)

The zero ﬁeld magnetization (spontaneous magnetization) is obtained as

µN

=tanh



µN



. (1.0.15)

The solution can be obtained graphically as shown in Fig. 1.4

Clearly, for high temperatures,

< 1, there is no magnetization. The only

solution is M =0. For

> 1, there are two solutions M =0 and a ﬁnite value

of M. It is the ﬁnite value of M which gives a lower free energy and hence there

is a critical temperature T

deﬁned by

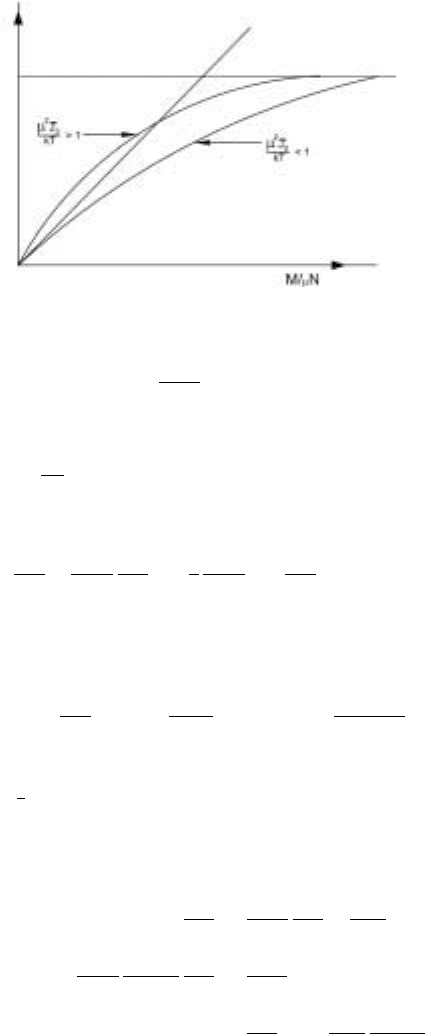
8 1 Introduction

Figure 1.4. The graphical solution of Eq.(1.15)

=1, (1.0.16)

which separates a phase of zero spontaneous magnetization (paramagnetic) from

a phase of non-zero spontaneous magnetization (ferromagnetic).

To ﬁnd how big

µN

is in the ordered phase, we expand the right hand side of

Eq.(1.0.15), assuming T is such that the argument of the hyperbolic tangent is still

small. Then,

µN

−







µN



+..... (1.0.17)

In the second term on the right hand side, we can replace T by T

since we are

interested in the region T T

. Using Eq.(1.0.16), and the fact that M/µN =0,

we ﬁnd



µN



 3





−T)=3

−T)

or M ∝ (T

−T)

1/2

(1.0.18)

This leads to β =

when we compare with Eq.(1.0.1), independent of any material

dependent constant J

and T

In the presence of a small external ﬁeld H, the Taylor expansion of Eq.(1.0.14)

for T>T

leads to

µN



µN

T −T

µN



∂M

∂H





T −T

(1.0.19)