Birge J.R., Louveaux F. Introduction to Stochastic Programming

Подождите немного. Документ загружается.

134 3 Basic Properties and Theory

Assume that the ﬁrst 9 scenarios (restricted to wheat’s and corn’s yields) are as

follows: (2.25,2.4) , (2.1,2.6) , (2.4,2.5) , (2.6,2.3) , (2.2, 3) , (2,3.4) , (2.5,2.7) ,

(2.3,3.6) , (2.2, 3.7) . They are represented in Figure 1. Assume also that, for all

other scenarios, P(A

) > 0.8 ; hence, w

= 0.

Fig. 1 Wheat and corn’s scenarios.

There are several dominance relations:

≥

, implying valid inequalities

≤w

, w

≤w

, w

≤w

, w

≤w

, w

≤w

, w

≤w

, w

≤w

, w

≤w

≤ w

Dominance sets A

can be visualized by drawing an horizontal and a vertical

half-line from k . A

and A

are illustrated in Figure 1. A

= {2,5} with P(A

0.08 and A

= {1,2, 3,7} with P(A

)=0.16 . Even if P(A

)+P(A

) > 0.2,

Scenarios 5 and 7 do not constitute a cover as P(A

∪A

)=0.2 . Scenarios 3 and 9

have similar probabilities and constitute a cover: A

= {1, 3} with P(A

)=0.08 ,

= {2,5,6, 9} with P(A

)=0.16 and P(A

∪A

)=0.24 . Thus w

+ w

≤1is

a valid inequality. This example shows that covers based on the dominance sets A

are difﬁcult to ﬁnd as probabilities do not sum over sets that may intersect.

Only minimal covers are of interest. As an example, { 1,3, 9} is a cover but it is

not minimal as removing {1} still forms a cover. There are several other minimal

covers in this example: {1,4,9}, {3,4,5,6}, {3,8}, {4,5, 7}, {4,6,7}, {4,8},

{7,8}{7,9}, {8,9}. In general, the MILP only adds minimal covers if they are vi-

olated by the current fractional point. The problem of efﬁcient techniques for ﬁnding

a violated minimal cover based on dominance sets is studied in Ruszczy´nski [2002].

This paper also provides a more general treatment on the cases that create what we

have called here dominance.

3.3 Stochastic Integer Programs 135

Exercises

9. Consider Example 2 in Section 3.2b. Instead of putting a limit on the total pur-

chase of wheat and corn, the farmer does not want either purchase to be over

10 T. Thus, (2.17) is replaced by P(y

(

) ≤ 10,y

(

) ≤ 10) ≥ 0.80 . Show

how to reformulate the recourse problem with K scenarios and this extra prob-

abilistic constraint as a MILP with K extra binary variables and 2K + 1extra

constraints.

10. Consider Section 3.2b. Restart from the original farming problem of Section 1.1

without a probabilistic constraint on the total purchase of wheat and corn. The

farmer now concentrates on sugar beet production. He ﬁnds it inappropriate to

sell less than 5400 T of sugar beets at the favorable price or more than 300 T

of sugar beets at the lower price. If either of these events happen, he considers

the sugar beet production planning as unsuccessful. Assume he wants a produc-

tion planning which maximizes its expected proﬁt, with the constraint that the

probability of an unsuccessful sugar beet production planning is no more than

20%.

(a) Show how to reformulate the recourse problem with K scenarios and the

extra probabilistic constraint on sugar beet production planning as a MILP

with K extra binary variables and 2K + 1 extra constraints.

(b) Is it still possible to get a dominance result based on the yield of sugar beet

production?

3.3 Stochastic Integer Programs

a. Recourse problems

The general formulation of a two-stage integer program resembles that of the gen-

eral linear case presented in Section 1.1. It simply requires that some variables, in

either the ﬁrst stage or the second stage, are integer. As we have seen in the exam-

ples in Chapter 1, in many practical situations the restrictions are, in fact, that the

variables must be binary, i.e., they can only take the value zero or one. Formally, we

may write

min

x∈X

z = c

x + E

min{q(

)

) |Wy(

)=h(

) −T(

)x,y(

) ∈Y a. s. }

s. t. Ax = b ,

where the deﬁnitions of c , b , ξ , A , W , T ,and h are as before. However, X

and/or Y contains some integrality or binary restrictions on x and/or y . With this

deﬁnition, we may again deﬁne a deterministic equivalent program of the form

136 3 Basic Properties and Theory

min

x∈X

z = c

x + Q(x)

s. t. Ax = b

with Q(x) the expected value of the second stage deﬁned as in Section 3.1.

In this section, we are interested in the properties of Q(x) and K

= {x |Q(x) <

∞}. Clearly, if the only integrality restrictions are in X , the properties of Q(x) and

are the same as in the continuous case. The main interesting cases are those in

which some integrality restrictions are present in the second stage. The properties of

Q(x,

) for given

are those of the value function of an integer program in terms

of its right-hand side. This problem has received much attention in the ﬁeld of in-

teger programming (see, e.g., Blair and Jeroslow [1982] or Nemhauser and Wolsey

[1988]). In addition to being subadditive, the value function of an integer program

can be obtained by starting from a linear function and ﬁnitely often repeating the

operations of sums, maxima, and non-negative multiples of functions already ob-

tained and rounding up to the nearest integer. Functions so obtained are known as

Gomory functions (see again Blair and Jeroslow [1982] or Nemhauser and Wolsey

[1988]). Clearly, the maximum and rounding up operations imply undesirable prop-

erties for Q(x,

) , Q(x) ,and K

, as we now illustrate. General proofs can be

found in Louveaux and Schultz [2003].

Proposition 20. The expected recourse function Q(x) of an integer program is in

general, lower semicontinuous, nonconvex and discontinuous.

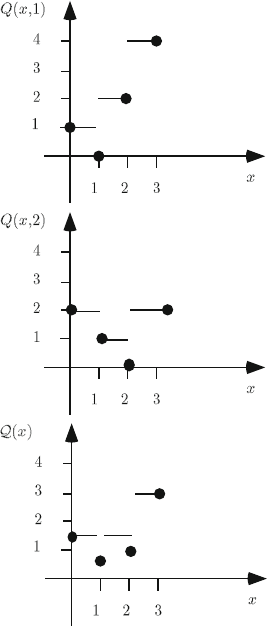
Example 5

We illustrate the proposition in the following simple example where the ﬁrst stage

contains a single decision variable x ≥0 and the second-stage recourse function is

deﬁned as:

Q(x,

)=min{2y

+ y

| y

≥ x −

, y

≥

−x , y ≥ 0 , integer}. (3.1)

Assume ξ can take on the values one and two with equal probability 1/2.Let a

denote the smallest integer greater than or equal to a (the rounding up operation)

and a the truncation or rounding down operation ( a= −−a). Consider

1.For x ≤1 , the optimal second-stage solution is y

= 0, y

= 1−x.For x ≥1,

it is y

=  x −1, y

= 0 . Hence, Q(x, 1)=max{2(x −1), 1 −x}, a typical

Gomory function. It is discontinuous at x = 1 . Nonconvexity can be illustrated

by Q(0.5,1) > 0.5Q(0,1)+0.5Q(1,1) . Similarly, Q(x,2)=max{2(x −2), 2−

x}. The three functions, Q(x,1) , Q(x,2) ,and Q (x) are represented in Figure 2

The recourse function, Q(x) , is clearly discontinuous in all positive integers.

Nonconvexity can be illustrated by Q(1.5)=1.5 > 0.5Q(1)+0.5Q(2)=0.75 .

Thus Q(x) has none of the properties that one may wish for to design an algorithmic

3.3 Stochastic Integer Programs 137

procedure. Note, however, that a convexity-relatedproperty exists in the case of sim-

ple integer recourse (Proposition 8.4) and that it applies to this example.

Fig. 2 Example of discontinuity.

Continuity of the recourse function can be regained when the random variable is

absolutely continuous (Stougie [1987]).

Proposition 21. The expected recourse function Q(x) of an integer program with

an absolutely continuous random variable is continuous.

Note, however, that despite Proposition 21, the recourse function Q(x) remains,

in general, nonconvex.

138 3 Basic Properties and Theory

Example 6

Consider Example 5 but with the (continuous) random variable deﬁned by its cu-

mulative distribution,

F(t)=P(ξ ≤t)=2 −2/t, 1 ≤t ≤ 2 .

Consider 1 < x < 2. For 1≤

< x ,wehave 0< x −

< 1 ; hence, y

= 1,

= 0 , while for x <

≤ 2,wehave 0<

−x ≤ 1 ; hence, y

= 0, y

= 1.

It follows that

Q(x)=



2dF(t)+



1dF(t)=2F(x)+1 −F(x)

= F(x)+1 = 3 −2/x ,

which is easily seen to be nonconvex.

Properties are just as poor in terms of feasibility sets. As in the continuous case,

we may deﬁne the second-stage feasibility set for a ﬁxed value of ξ as K

(

)) =

{x | there exists y s.t. Wy = h(

) −T(

)x,y ∈Y} where

(

) is formed by the

stochastic components of h(

) and T(

) .

Proposition 22. The second-stage feasibility set K

(

) is in general

nonconvex.

Proof: Because K

(

)={x | Q(x,

) < ∞}, nonconvexity of K

(

) immediately

follows from nonconvexity of Q(x,

) .

A simple example sufﬁces to illustrate this possibility.

Example 7

Let the second stage of a stochastic program be deﬁned as

−y

+ y

≤ ξ −x

, (3.2)

+ y

≤ 2 −x

, (3.3)

≥ 0 and integer. (3.4)

Assume ξ takes on the values 1 and 2 with equal probability 1/2. We then

construct K

(1) .

By (3.3), x

≤ 2 is a necessary condition for second-stage feasibility. For 1 <

≤ 2 , the only feasible integer satisfying (3.3)is y

= y

= 0 . This point is also

feasible for (3.2)if

−x

≥ 0,i.e.,if x

≤ 1.

For 0 < x

≤ 1 , the integer points y satisfying (3.3)are (0,0) , (0,1) , (1,0) .

The one yielding the smallest left-hand side (and thus the most likely to yield points

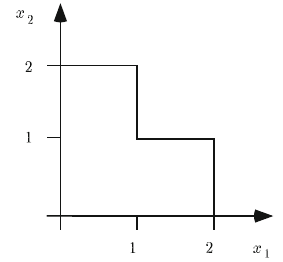
3.3 Stochastic Integer Programs 139

Fig. 3 Feasibility set for Example 7.

in K

(1)) is (1,0) . It requires ξ −x

≥−1,i.e., x

≤ 2.Hence K

(1) is as in

Figure 3 and is clearly nonconvex. It may be represented as K

(1)={x | min{x

−

1,x

−1}≤0,0 ≤ x

≤ 2, 0 ≤x

≤ 2} and is again a typical Gomory function due

to the minimum operation.

We may then deﬁne the second-stage feasibility set K

as the intersection of

(ξ) over all possible ξ values. This deﬁnition poses no difﬁculty when ξ has a

discrete distribution. In Example 7, K

= K

(1) and is thus also nonconvex.

Computationally, it might be very useful to have the constraint matrix of the

extensive form totally unimodular. (Recall that a matrix is totally unimodular if

the determinants of all square submatrices are 0 , 1 , or −1 .) This would imply

that any solution of the associated stochastic continuous program would be integer

when right-hand sides of all constraints are also integer. A widely used sufﬁcient

condition for total unimodularity is as follows: all coefﬁcients are 0 , 1 , or −1;

every variable has at most two nonzero coefﬁcients and constraints can be separated

in two groups such that, if a variable has two nonzero coefﬁcients and if they are

of the same sign, the two associated rows belong to different sets and if they are of

opposite signs they belong to the same set.

To help understand the sufﬁciency condition, consider the following

matrix

⎛

⎝

101−1

0110

−110 1

⎞

⎠

as an example. For this matrix, one set consists of Rows 1 and 3, and the second

set contains just Row 2. The constraint matrix of the extensive form of a nontrivial

stochastic program cannot satisfy this sufﬁcient condition. For simplicity, consider

the case of a ﬁxed T matrix. Assume that any variable that has a nonzero coefﬁcient

in T also has a nonzero coefﬁcient in A . Then, if |

|≥2 , the constraint matrix

of the extensive form contains a submatrix

140 3 Basic Properties and Theory

⎛

⎝

⎞

⎠

that has at least three nonzero coefﬁcients. Thus, only very special cases (a random

T matrix with every column having a nonzero element in only one realization, for

example) could lead to totally unimodular matrices.

Last but not least, it should be clear that just ﬁnding Q(x) for a given x becomes

an extremely difﬁcult task for a general integer second stage. This is especially

true because there is no hope to use sensitivity analysis or some sort of bunching

procedure (see Section 5.4)toﬁnd Q(x,ξ) for neighboring values of

. Cases

where Q(x) can be computed or even approximated in a reasonable amount of

time should thus be considered exceptions. One such exception is provided in the

next section.

b. Simple integer recourse

Let ξ be a random vector with support

in ℜ

, expectation

, and cumulative

distribution F with F(t)= P{

≤ t}, t ∈ R

. A two-stage stochastic program

with simple integer recourse is as follows:

SIR minz = c

x + E

{min(q

)

+(q

−

)

−

≥ ξ −Tx, y

−

≥ Tx−ξ ,

∈Z

, y

−

∈ Z

a. s. }

s. t. Ax = b , x ∈ X , (3.5)

where X typically deﬁnes either non-negative continuous or non-negative integer

decision variables and where we use ξ = h because both T and q are known and

ﬁxed. As in the continuous case, we may replace the second-stage value function

Q(x) by a separable sum over the various coordinates. Let

= Tx be a tender to

be bid against future outcomes. Then Q(x) is separable in the components

Q(x)=

∑

i=1

(

) , (3.6)

with

(

)=E

(

,ξ

) (3.7)

and

(

)=min{q

+ q

−

| y

≥ ξ

−

≥

−ξ

, y

−

∈ Z

} . (3.8)

3.3 Stochastic Integer Programs 141

As in the continuous case, any error made in bidding

versus

must be com-

pensated for in the second stage, but this compensation must now be an integer.

Now deﬁne the expected shortage as

(

)=E ξ

−



and the expected surplus as

(

)=E

−ξ



where x

= max{x,0}. It follows that

(

) is simply

(

)=q

(

)+q

−

(

As is reasonable from the deﬁnition of SIR, we assume q

≥ 0,q

−

≥ 0.

Studying SIR is thus simply studying the expected shortage and surplus. Unless

necessary, we drop the indices in the sequel. Let ξ be some random variable and

x ∈ ℜ . The expected shortage is

u(x)=Eξ −x

(3.9)

and the expected surplus is

v(x)=Ex −ξ

. (3.10)

For easy reference, we also deﬁne their continuous counterparts. Let the continuous

expected shortage be

ˆu(x)=E(ξ −x)

(3.11)

and the continuous expected surplus be

ˆv(x)=E(x −ξ)

. (3.12)

First observe that Example 5 (and 6) is a case of a stochastic program with simple

recourse, from which we know that u(x)+v(x) is in general nonconvex and dis-

continuous unless ξ has an absolutely continuous probability distribution function.

We thus limit our ambitions to study ﬁniteness and computational tractability for

u(·) and v(·) . The following results appear in Louveaux and van der Vlerk [1993].

Proposition 23. The expected shortage function is a non-negative non-decreasing

extended real-valued function. It is ﬁnite for all x ∈ ℜ if and only if

Emax{ξ,0} is ﬁnite.

Proof: We only give the proof for ﬁniteness because the other results are immedi-

ate. First, observe that for all t in ℜ ,

(t −x)

≤t −x

≤ (t −x + 1)

≤ (t −x)

+ 1 .

Taking expectation yields

142 3 Basic Properties and Theory

ˆu(x) ≤ u(x) ≤ ˆu(x −1) ≤ ˆu(x)+1 . (3.13)

The result follows as ˆu(x) is ﬁnite if and only if

is ﬁnite.

We now provide a computational formula for u(x) .

Theorem 24. Let ξ be a random variable with cumulative distribution function

F.Then

u(x)=

∞

∑

k=0

(1 −F(x + k)) . (3.14)

Proof: Following the previous deﬁnitions, we have:

∞

∑

k=0

(1 −F(x + k)) =

∞

∑

k=0

P{ξ −x > k}

∞

∑

k=0

∞

∑

j= k+1

P{ξ −x

= j}

∞

∑

j= 1

j− 1

∑

k=0

P{ξ −x

= j}

∞

∑

j= 1

jP{ξ −x

= j} = Eξ −x

= u(x) ,

which completes the proof.