Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

INSIGHT

Although the function f of Example 13 does not have a maximum or

minimum value on I 5 ð21; 1Þ, the Extreme Value Theorem is not contradicted because

I is not closed. It is incorrect to assume, however, that there cannot be a maximum or

minimum value when the Extreme Value Theorem does not apply. The function x /x

has a minimum value 0 on I, the function x/1 2 x

has a maximum value 1 on I, and the

function x/cosð 2πxÞ has a maximum value 1 and a minimum value 21onI.

QUICK QUIZ

1. True or false: If c is in the domain of f, and lim

x-c

f ðxÞ exists, then f is continuous

at c.

2. At what points is f ðxÞ5 sinðx

Þ=ðx

2 16Þ continuous? Is f a continuous

function?

3. True or false: If f : ½0; 3-ð0; 1, then f has a minimum value.

4. True or false: If f : ½0; 3-ð0; 1 is continuous, then f has a minimum value.

5. True or false: If f : ð0; 1-½0; 3 is continuous, then f has a maximum value.

Answers

1. False 2. At every point of its domain, fx 2 R : x 6¼ 62g;

Yes 3. False

4. True 5. False

EXERCISES

Problems for Practice

c In each of Exercises 124, determine at which of the

points 21, 1, and 2 the given function f is continuous. b

1. f ðxÞ5

2 1ifx , 2

3ifx 5 2

3 sinðπ=xÞ if 2 , x

2. f ðxÞ5

1 2 x if x #21

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

5 2 x

if 21 , x , 1

2 2 cosðπxÞ if 1 # x

3. f ðxÞ5

ðx

2 1Þ=ðx

1 1Þ if x #21

ð3x12Þ

1=3

if 21 , x , 2

4 2 x if 2 # x

4. f ðxÞ5

ðx

2 xÞ=ðx

2 1Þ if x ,21

2x 1 1if21 # x # 2

ðx

2 4Þ=ðx 2 2Þ if 2 , x

c In Exercises 5224, determine the values at which the given

function f is

continuous. Remember that if c is not in the

domain of f, then f cannot be continuous at c. Also remember

that the domain of a function that is deﬁned by an expression

consists of all real numbers at which the expression can be

evaluated. b

5. f ðxÞ5 x

1 4

6. f ðxÞ5 2x 2 9

7. f ðxÞ5 1=ðx 1 1Þ

8. f ðxÞ5 x=ðx

2 x 2 5Þ

9. f ðxÞ5 1=ðx

1 1Þ

10. f ðxÞ5 1=ð1 2 x

11. f ðxÞ5

2 5x 1 6

1 x 2 12

12. f ðxÞ5

1 1ifx , 0

1=ð2x 1 1Þ if x $ 0



13. f ðxÞ5

x 1 1ifx # 3

6ifx . 3



14. f ðxÞ5

2 2ifx # 3

8ifx . 3



15. f ðxÞ5

ðx11Þ

if x ,24

2 20x 1 1ifx $24



16. f ðxÞ5

ðx

=4Þ2 7ifx , 6

2ifx 5 6

9 2 x if x . 6

17. f ðxÞ5

2x 2 19 if x , 7

25ifx 5 7

2 2 x if x . 7

18. f ðxÞ5

2x 1 1ifx , 0

4ifx 5 0

2 2ifx . 0

19. f ðxÞ5

ðx

2 1Þ=ðx 1 1Þ if x 6¼ 21

2ifx 521



20. f ðxÞ5

ðx

2 1Þ=ðx 1 1Þ if x 6¼ 21

cosðπxÞ2 1ifx 521



21. f ðxÞ5

sinðxÞ=x if x 6¼ 0

0ifx 5 0



22. f ðxÞ5

tanðxÞ=x if x 6¼ 0

1ifx 5 0



2.3 Continuity 115

23. f ðxÞ5

2 3ifx # 3

ðx

2 9Þ=ðx 2 3Þ if x . 3



24. f ðxÞ5

ﬃﬃﬃ

 tanðxÞ1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

π 2 x

 cscðxÞ

c In each of Exercises 25228, deﬁne F(2)

to obtain a con-

tinuous extension F of f. b

25. f ðxÞ5

1 7ifx , 2

1 3ifx . 2



26. f ðxÞ5

5=ðx

1 6Þ if x , 2

1=x if x . 2



27. f ðxÞ5

=ð18 2 xÞ if x , 2

=ðx 1 2Þ if x . 2



28. f ðxÞ5

=ðx

1 1Þ if x , 2

=ðx

1 2Þ if x . 2



c For Exercises 29232, determine the points at which the

function

is left-continuous, the points at which the function is

right-continuous, and the points at which the function is

continuous. Give reasons for your answers. b

29. f ðxÞ5

fx # 5

3ifx . 5



30. gðxÞ5

2 15 if x ,24

1ifx $24



31. f ðxÞ5

x 1 1ifx , 3

2ifx $ 3



32. gðxÞ5

if x , 0

2x if x $ 0



c In Exercises 33238, a continuous function f is

deﬁned on a

closed, bounded interval I. Determine the extreme values of

the function f. Sketch the graph of f and label the points at

which f assumes its extreme values. b

33. f ðxÞ5 x

1 2x 1 3; I 5 ½23; 22

34. f ðxÞ5 x

1 2x 1 3; I 5 ½22; 1

35. f ðxÞ5 x

1 2x 1 3; I 5 ½1; 2

36. f ðxÞ5 11 1 6x 2 x

; I 5 ½1; 4

37. f ðxÞ5 2 2 cosðxÞ; I 5 ½0; 2π

38. f ðxÞ5 x 1 sinðxÞ; I 5 ½2π; π

c In each of Exercises 39242, a continuous function f is

deﬁned

on a closed, bounded interval I. A consequence of the

Intermediate Value Theorem is that there is an interval ½α; β

with the property that, for every γ between α and β, the

equation f ðxÞ5 γ has a solution x 5 c with c in I. What are α

and β? b

39. f ðxÞ5 sinðxÞ; I 5 ½2π=6; π=4

40. f ðxÞ5 x 1 24=x; I 5 ½2; 6

41. f ðxÞ5 ð7x 2 3x

Þ=8; I 5 ½1; 2

42. f ðxÞ5

1 1

1 x 1 2

; I 5 ½23; 5

Further Theory and Practice

c In each of Exercises 43246, a function, f with domain

ð2N; 1Þ,ð3; NÞ is given. Deﬁne FðxÞ5 ax 1 b for 1 # x # 3

and FðxÞ5 f ðxÞ for x not in ½1; 3. Determine a and b so that F

is continuous. b

43. f ðxÞ5

fx , 1

26ifx . 3



44. f ðxÞ5

1 16 if x , 1

x 2 4ifx . 3



45. f ðxÞ5

ðx 1 1Þ=ðx

1 2Þ if x , 1

if x . 3



46. f ðxÞ5

cosðπxÞ if x , 1

sinðπxÞ if x . 3



c In each of Exercises 47250, determine at which points the

given

function is discontinuous. b

47. f ðxÞ5

sinðπx=2Þ if x is

not an integer

0ifx is an integer



48. f ðxÞ5

cosðπ=2Þ if x is not an integer

1ifx is an integer



49. f ðxÞ5

2cosðπ x=3Þ if x is not an integer

1ifx is an integer



50. f ðxÞ5

cosðπ x=4Þ if x is not an integer

sinðπ x=4Þ if x is an integer



51. For each of the four functions,

f ðxÞ5

2 1

x 2 1

; gðxÞ5

(

x 1 1ifx 6¼ 1

2ifx 5 1

;

hðxÞ5 x 1 1; and kðxÞ5

(

x 1 1ifx 6¼ 1

1ifx 5 1

;

compute the left and right limits at c 5 1, determine if it has

alimitatc 5 1, and determine if it is continuous at c 5 1.

(Pay particular attention to the domains of the functions.)

52. Show that the single ﬁler tax function T of Example 3,

Section 1.4 is a continuous function.

53. Consider the single ﬁler tax function T that is given in

Example 3 from Section 1.4. There are six tax brackets

that correspond to six marginal tax rates: 10%, 15%,

25%, 28%, 33%, and 35%. Suppose the tax brackets are

not altered, but the marginal tax rates are reduced to 8%,

12%, 16%, 20%, 25%, and 30%. What is the new tax

function, assuming it is continuous?

54. Prove that a function f is continuous at c if and only if f is

both left-continuous at c and right-continuous at c.

55. For any real number x, let bxc denote the greatest integer

which does not exceed x.

a. What is lim

x-3

bxc? Prove it.

b. What is lim

x-2

b4 2 2xc? Prove it.

c. What is lim

x-0

b1=bxcc? Prove it.

d. What is lim

x-0

bb2xcc=x? Prove it.

116 Chapter 2 Limits

56. The function f ðxÞ5 4 2 ðx22Þ

assumes a maximum

value on the interval I 5 (0, 4). What is that value? By

determining the image of f (x) for x in I, show that f

assumes no minimum value on I. Why is the Extreme

Value Theorem not contradicted?

57. Suppose a train pulls out of a station and comes to a stop

at the next station 80 km away exactly 1 h later. Assuming

the velocity of the train is a continuous function, prove

that, at some moment, the train must have been traveling

at a velocity of precisely 60 km/h.

58. Let p be a polynomial of odd degree and leading coefﬁ-

cient 1. It can be shown that lim

x-N

pðxÞ5 N and

lim

x-2N

pðxÞ52N. Use these facts and the Intermediate

Value Theorem to prove that p has at, least one real root.

59. Show that 10x

2 7x

1 20x 2 14 5 0 has a root in ð 0; 1Þ.

Deduce that 10 sin

ðxÞ2 7 sin

ðxÞ1 20 sinð xÞ2 14 5 0

has a solution.

60. Use the Intermediate Value Theorem to prove that

pðxÞ5 3x

2 7x

1 1 has three real roots and that they are

located in the intervals (21, 0), (0, 1), and (1, 2).

61. Because pðxÞ5 x

1 x 1 1 has odd degree, we can be sure

(by Exercise 58) that it has at least one real root.

Determine a ﬁnite interval that contains a root of p.

Explain why.

62. Use the Intermediate Value Theorem to show that

x/2 5 sin (x) has a positive solution. (Consider the func-

tion f ðxÞ5 x=2 2 sinðxÞ and the points a 5 π/6 and

b 5 2.1.)

63. Use the Intermediate Value Theorem to show that

pðxÞ5 10x

1 46x

2 39x

2 39x 1 36 has at least two

roots between 1 and 3.

c In each of Exercises 64267, an assertion is made about a

function p that

is continuous on the closed interval I 5 ½21; 3

and for which pð21Þ5 4 and pð3Þ522. If the statement is

true, explain why. Otherwise, sketch a function p that shows it

is false. b

64. p has

at least one root in I.

65. p has at most one root in I.

66. p has exactly one root in I.

67. p has an old number of roots in I.

c In each of Exercises 68273, an assertion is made about a

function f that

is deﬁned on a closed, bounded interval. If the

statement is true, explain why. Otherwise, sketch a function f

that shows it is false. (Note: jf j is deﬁned by jf jðxÞ5 jf ðxÞj.) b

68. If f is

continuous, then jf j is continuous.

69. If f is continuous, then f is continuous.

70. If f is continuous, then f

is continuous.

71. If f

is continuous, then f is continuous.

72. If f is continuous, then its image is a closed, bounded

interval.

73. If f has no maximum, then f is discontinuous at some

point of interval.

74. Suppose that α is a constant in the interval (0, 1). By

applying the Intermediate Value Theorem to

f ðxÞ5 α 2 sinðxÞ=x and using lim

x-0

sinðxÞ=x 5 1, show

that the equation α 5 sin (x) has a positive solution in x.

c Exercises 75277 illustrate the following theorem: If the

range

of f is contained in the domain of g, if lim

x-c

f ðxÞ5 ‘,

and if lim

y-‘

gðyÞ5 L, then lim

x-c

gðf ðxÞÞ5 gð‘Þ or

lim

x-c

gðf ðxÞÞ5 L or lim

x-c

gðf ðxÞÞ does not exist. b

75. Let gðxÞ5

fx 6¼ 0

1ifx 5 0



and f (x) 5 0 for all x. Let c 5 0. Evaluate ‘ and L. Show

that lim

x-0

gðf ðxÞÞ5 gð‘Þ, and compare this result with

Theorem 2.

76. Let g be deﬁned as in Exercise 75. Let f (x) 5 x. Let c 5 0.

Evaluate ‘ and L. Show that lim

x-0

gðf ðxÞÞ5 L, and

compare this result with Theorem 2.

77. Let g be deﬁned as in Exercise 75. Let

f ðxÞ5

x if x is irrational

0ifx is rational



Show that lim

x-0

gðf ðxÞÞ does not exist, and compare this

result with Theorem 2.

78. Let f : ½0; 1-½0; 1 be a continuous function. Prove that

there is a number c,0# c # 1, such that f (c) 5 c. Such a

value is said to be a ﬁxed point of f.(Hint: Think about

the function g(x) 5 f (x) 2 x.)

79. A hiker walks up a mountain path. He starts at the bottom

of the path at 8:00

AM and reaches the top at 6:00 PM.The

next morning, he starts down the same path at 8:00

AM and

reaches the bottom at 6:00

PM. Show that there is at least

one time of the day such that on each day the hiker’s

elevation was the same. Illustrate this by giving a repre-

sentative sketch of the ascent and descent elevation

functions in the rectangle ½0h; 10 h3 ½0; L where L is the

elevation of the peak.

80. The polynomial pðxÞ5 x

1 x 2 10

has exactly one real

root c. Find an integer k such that c is in the interval

(k, k 1 1).

81. Prove that, if f is a continuous function on [0, 1], and

f (0) 5 f (1) then there is a value c in (0, 1) such that

f (c) 5 f (c 1 1/2). This is a special case of the Horizontal

Chord Theorem.(Hint: Apply the Intermediate Value

Theorem to the function g deﬁned on [0, 1/2] by g(x) 5

f (x 1 1/2) 2 f (x).)

Calculator/Computer Exercises

82. Locate, to four decimal places of accuracy, the maximum

and minimum values of the function h(x) 5

2 5x

1 7x 1 9 on the interval [0, 4].

2.3 Continuity 117

83. Use Exercise 58 to explain why p(tan(x)) 5 c has a real

solution x for any real value of c and any cubic real

polynomial p. Approximate a solution to tan

(x) 1

3 tan (x) 5 19.

84. Graph f (x) 5 (x

2 3x 1 1)/(x

2 3x 2 1) in the viewing

rectangle [ 2 3, 3] 3 [215, 15]. Locate the points, to four

decimal places, at which f does not have a continuous

extension.

c In Exercises 85288, graph the given function f over

interval centered about the given point c, and determine if f

has a continuous extension at c. b

85. f ðxÞ5 x=jxj; c 5 0

86. f ðxÞ5 ðx

2 6x

1 7x

1 4x 2 4Þ=ðx22Þ

; c 5 2

87. f ðxÞ5 ðx

2 6x

1 7x

1 4x 2 4Þ=ðx 2 2Þ; c 5 2

88. f ðxÞ5 x

sinðxÞ=ð

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x

2 1Þ; c 5 0

89. Use the factorization

2 10x

1 38x

2 64x 1 40 5 ðx

2 6x 1 10Þðx22Þ

to show that

pðxÞ5 x

2 10x

1 38x

2 64x 1 50 $ 10:

For what values of γ does p(x) 5 γ have a real solution?

Show that p(x) 5 20 has a solution in each of the intervals

(0,1) and (4, 5). Find these solutions to four decimal places.

90. Let f (x) 5 (3x 2 sin (2x))/x for 2 2 # x # 4, x 6¼ 0. Locate

the extreme values of f to four decimal places.

91. Let f (x) 5 cos

(x 2 π/3) sin (x)/x for 22 # x # 2, x 6¼0.

Locate the extreme values of the continuous extension of

f to four decimal places.

2.4 Inﬁnite Limits and Asymptotes

Consider the graph of the equation y 5 1/x in Figure 1. Observe that y becomes

arbitrarily large and positive as x - 0

. Pict orially, the graph approaches the

positive y-axis. Also, as x - 0

, the ordinate y becomes ne gative without bound.

Pictorially, the graph approaches the negative y-axis. Also, as x-6N, the graph

approaches the horizontal line y 5 0. In this section, we develop a precise languag e

for describing this type of behavior of graphs.

Inﬁnite-Valued Limits It is convenient to extend the notion of limit. Up to now, we have agreed that the

limits lim

x-0

1=x and lim

x-0

1=x do not exist. For the limit lim

x-0

1=x to exis t,

there woul d have to be a real number ‘ to which the values of 1/x would tend as x

approached 0 from the right. As the graph of y 5 1/x in Figure 1 shows, no such real

number can exist. The graph is, in fact, unbounded. For similar reasons, lim

x-0

1=x

cannot equal a real number. The deﬁnition of “limit” that we now give extends our

existing deﬁnition so that ‘ is allowed to be inﬁnite.

DEFI NITION

Let f be a function that is deﬁned on an open interval just to the

left of c and also on an interval just to the right of c. We write

lim

x-c

f ðxÞ51N

if f (x) become s arbitrarily large and positive as x - c. We write

lim

x-c

f ðxÞ52N

if f (x) become s arbitrarily large and negative without bound as x-c.

More rigorously, lim

x-c

f ðxÞ51N if, for any N . 0, there is a δ . 0 such

that f (x) . N whenever 0 , jx 2 cj, δ: Also, lim

x-c

f ðxÞ52N if for any M , 0

there is a δ . 0 such that f (x) , M whenever 0 , jx 2 cj, δ:

The one-sided limits lim

x-c

f ðxÞ56N and lim

x-c

f ðxÞ56N are deﬁned

similarly.

y 

m Figure 1

118 Chapter

2 Limits

INSIGHT

The symbol N is used many times in this section. It does not represent a

real number. It is merely a convenient piece of notation for certain unbounded behavior.

The deﬁnitions of lim

x-c

f ðxÞ56N provide an analytic basis with which to

investigate inﬁnite limits. In practice, the graph of a function with an inﬁnite limit

will clearly indicate this behavior. Often we determine where a denominator of f (x)

vanishes in order to locate possible points c at which lim

x-c

f ðxÞ might be 6N. For

example, the denominator cos (x) in sin (x)/cos (x) vanishes at x 5 π/2 and

lim

x-π=2

tan ðxÞ5 lim

x-π=2

sinðxÞ

cosðxÞ

52N;

as shown in Figure 2.

⁄ EX

AMPLE 1 Analyze the following limits:

a. lim

x-21

ðx 1 1Þ

b. lim

x-π=2

sec ðxÞ

c. lim

x-π=2

sec ðxÞ

d. lim

x-2

ðx 2 2Þ

Solution By inspection, we ﬁnd:

a. lim

x-21

ðx 1 1Þ

51N (see Figure 3),

b. lim

x-π=2

sec ðxÞ51N (see Figure 4),

c. lim

x-π=2

sec ðxÞ52N (see Figure 5),

d. lim

x-2

ðx 2 2Þ

52N (see Figure 6). ¥

Vertical Asymptotes The close connection between the ﬁgures and our perception of these limits sug-

gests the following deﬁnition.

tan(x)

m Figure 2

lim

x-π=2

tan ðxÞ52N

1.1 1.0 0.9

m Figure 3 The plot of

1=ðx 1 1Þ

in the viewing

rectangle [21.1, 20.9] 3 [0, 1000]

1.510.5

m Figure 4 The plot of sec (x)

in the viewing rectangle [0, π/2] 3

[0, 50]

50

32.52

m Figure 5 The plot of sec (x)

in the viewing rectangle [π/2, π] 3

[250, 0]

10

2.51.5

m Figure 6 The plot of

21=ðx 2 2Þ

in the viewing

rectangle [1.5, 2.5] 3 [210

,0]

2.4 Inﬁnite Limits and Asymptotes 119

DEFINITION

If a function f has a one-sided or two-sided inﬁnite limit as x-c,

then the line x 5 c is said to be a vertical asymptote of f.

In this circumstance, the graph of f becomes arbitrarily close to the vertical line

x 5 c, and the sketch of the graph of f should exhibit this line. In Figure 7,

the vertical asymptote is rendered as a dotted line. When lim

x-c

f ðxÞ51N,we

sometimes say the asymptote is upward vertical. When lim

x-c

f ðxÞ52N, we say

the asymptote is downward vertical. In the case of one-sided limits, we have four

possible behaviors: upward vertical from the left, upward vertical from the right,

downward vertical from the left, and downward vertical from the right.

⁄ EX

AMPLE 2 Discuss vertical asymptotes for the functions analyzed in

Example 1.

Solution The

graph of y 5 1=ðx11Þ

has x 521 as an upward vertical asymptote

because the denominator be comes arbitrarily small and positive when x is close to,

and on either side of, 21 (refer to Figure 3).

The function y 5 sec(x)h

asx 5 π/2 as an upward vertical asymptote from the

left and a downward vertical asymptote from the right (refer to Figures 4 and 5).

When x is just to the left of π/2, the denominator of 1/cos (x) is small and positive;

when x is just to the right of π/2, however, the denominator is small in absolute

value and negative.

Finally, y 521=ðx22Þ

has x 5 2 as a two-sided downward vertical asymptote

(refer to Figure 6). The denominator is small and positive when x is close to 2.

⁄ EXAMPLE 3 Examine the function gðxÞ5 x

=ðx

2 3x 2 4Þ for vertical

asymptotes.

Solution The

denominator factors as ( x 1 1) (x 2 4); hence it vanishes only at

x 521 and x 5 4. At all other values of x, the function g will be continuous; in

particular, it will have a ﬁnite limit and will certainly not have a vertical asymptote.

The only candidates for vertical asymptotes are x 521andx 5 4.

Write the function as

gðxÞ5

ðx 1 1Þðx 2 4Þ

When x is just to the left of 21, x

is positive (approximately 1), (x 1 1) is negative

and small in absolute value, and (x 2 4) is negative. Therefore

lim

x-1

gðxÞ5 lim

ðsmall 2Þð2Þ

51N:

Similar reasoning shows that

lim

x-1

gðxÞ5 lim

ðsmall 1Þð2Þ

52N

(the only difference this time is that (x 1 1) . 0).

m Figure 7 x 5 c is a vertical

asymptote.

120 Chapter 2 Limits

When x is just to the left of 4, x

is positive, (x 1 1) is positive, and (x 2 4) is

negative and small in absolute value. Therefore

lim

x-4

gðxÞ5 lim

ð1Þðsmall 2Þ

52N:

Similar reasoning shows that

lim

x-4

gðxÞ5 lim

ð1Þðsmall 1Þ

51N:

We conclude that g has x 521andx 5 4 as vertical asymptotes. It should be

noted that the asymptotes are one-sided. We obtain Figure 8 by using the preceding

information and plotting some points.

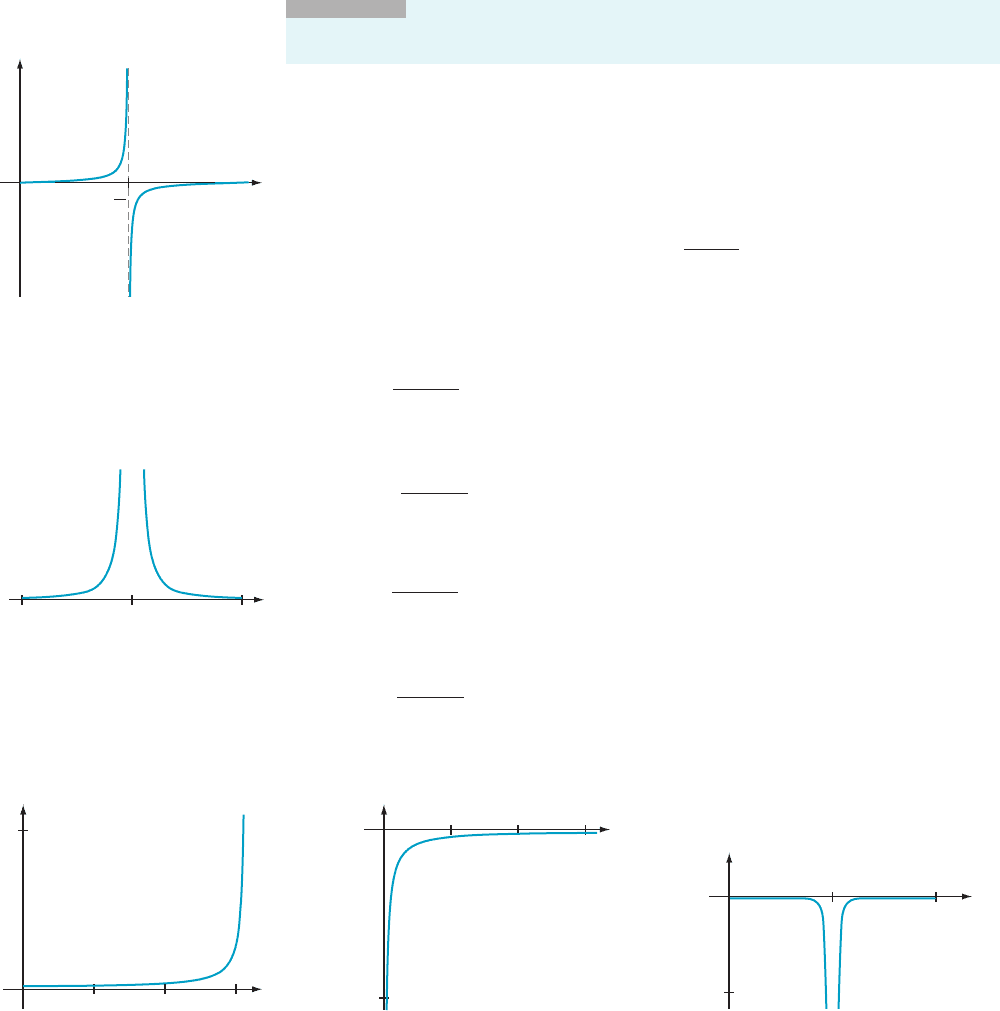
INSIGHT

The function g in Example 3 has a vertical asymptote at each point at

which it is undeﬁned. The same is true of the functions in Example 1. However, it is

incorrect to think that a function must have a vertical asymptote at a point at which it is

not deﬁned. Consider the function H(x) 5 sin (1/x), which is undeﬁned at x 5 0. Because

jHðxÞj is never greater than 1, H certainly cannot have 1N or 2N as a limit. So H(x) has

no vertical asymptote at x 5 0. In fact, H has no limit of any kind at 0, as shown in

Figure 9.

Limits at Inﬁnity Now we turn to the problem of identifying horizontal asymptotes. This requires

another notion of limit.

DEFINITION

Assume that the domain of f contains an interval of the form

(a, N) and let α be a ﬁnite real number. We say that

lim

x- 1N

f ðxÞ5 α

if f (x) approaches α when x becomes arbitrarily large and positive.

Now assume that the domain of g contains an interval of the form (2N, b).

Let β be a ﬁnite real number. We say that

lim

x- 2N

gðxÞ5 β

if g(x) approaches β when x is negative and becomes arbitrarily large in absolute

value.

More rigorously, lim

x-1N

f ðxÞ5 α if, for any ε . 0, there is an N such that

jf ðxÞ2 αj, ε whenever N , x , N. Also, lim

x-2N

gðxÞ5 β if, for any ε . 0,

there is an M such that jgðxÞ2 βj, ε whenever 2N , x , M.

⁄ EX

AMPLE 4 Examine the limits at inﬁnity for the function

f ðxÞ5

2 6x 1 8

1 4x 1 6

x  4

Vertical

asymptote

x  1

Vertical

asymptote

20

84 2264

m Figure 8 Graph of g (x) 5 x

2 3x 2 4)

1.0

0.10.1

1.0

1.0

H(x)  sin



m Figure 9 Inﬁnitely many

oscillations and no asymptotes

2.4 Inﬁnite Limits and Asymptotes 121

Solution A good rule of thu mb when studying the limits at inﬁnity of a rational

function (the quotient of polynomials) is to divide the numerator and denominator

by the highest power of x that appears in the denominator. We therefore divide the

numerator and denominator of f by x

(the highest power that appears in the

denominator) to obtain

f ðxÞ5

3 2 6=x 1 8=x

1 1 4=x 1 6=x

Now it is clear that as x - 1N or x - 2N, all terms vanish except the 3 in the

numerator and the 1 in the denominator. Thus we see that

lim

x - 1N

f ðxÞ5

3 1 0 1 0

1 1 0 1 0

5 3 and lim

x- 2N

f ðxÞ5

3 1 0 1 0

1 1 0 1 0

5 3:

This limiting behavior is visible in the plot of f in Figure 10, in which α 5 3.

Horizontal Asymptotes

DEFINITION

lim

x - 1N

f ðxÞ5 α;

then we say that the line y 5 α is a horizontal asymptote of f. Similarly, if

lim

x- 2N

f ðxÞ5 β;

then we say that the line y 5 β is a horizontal asymptote of f.

If the lin e L deﬁned by y 5 α is a horizontal asymptote of f, then the graph of f

becomes arbitrarily close to L. When we sketch the graph of f, we include the

horizontal asymptote L as a dotted line (refer to Figure 10). It may ha ppen that

both lim

x -1N

f ðxÞ5 α and lim

x-2N

f ðxÞ5 α. In this case, the line y 5 α is cer-

tainly a horizontal asymptote. However, the line would still be called an asymptote

if only one of these limits existed. If lim

x -1N

f ðxÞ5 α; and lim

x-2N

f ðxÞ5 β with

α 6¼β, then f has two distinct horizontal asymptotes.

In Figure 10, we would say that y 5 α is a right upper asymptote and a left

lower asymptote. Of course, another graph could have a right lower asymptote or a

left upper asymptote. The next example shows that a horizontal asymptote need

not be either upper or lower.

⁄ EX

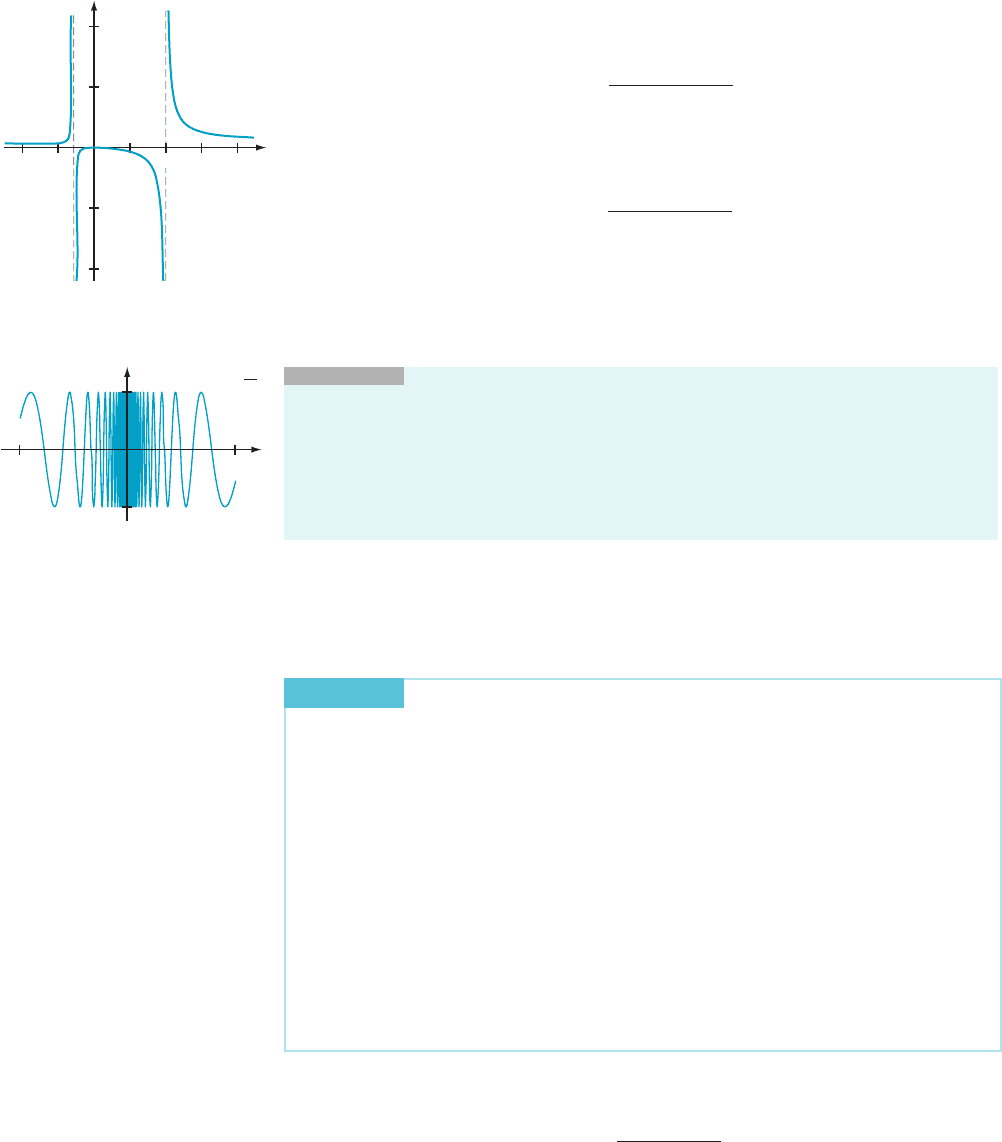
AMPLE 5 Analyze the graph of gðxÞ5 sinð2xÞ=ð1 1 x

Þ for horizontal

asymptotes.

Solution We

divide the numerator and denominator by the highest power of x that

appears in the denominator (namely, x

gðxÞ5

sinð2xÞ=x

ð1=x

Þ1 1

Because jsinð2xÞj # 1, it follows that sinð2xÞ=x

-0asx-6N. Similarly, 1=x

-0

as x-6N. Using limit rules that are parallel to those from Section 2.2 for ﬁnite

limits, we obtain

y  f(x)

y  a

m Figure 10 lim

x -2N

f ðxÞ5 α

and lim

x -1N

f ðxÞ5 α

122 Chapter 2 Limits

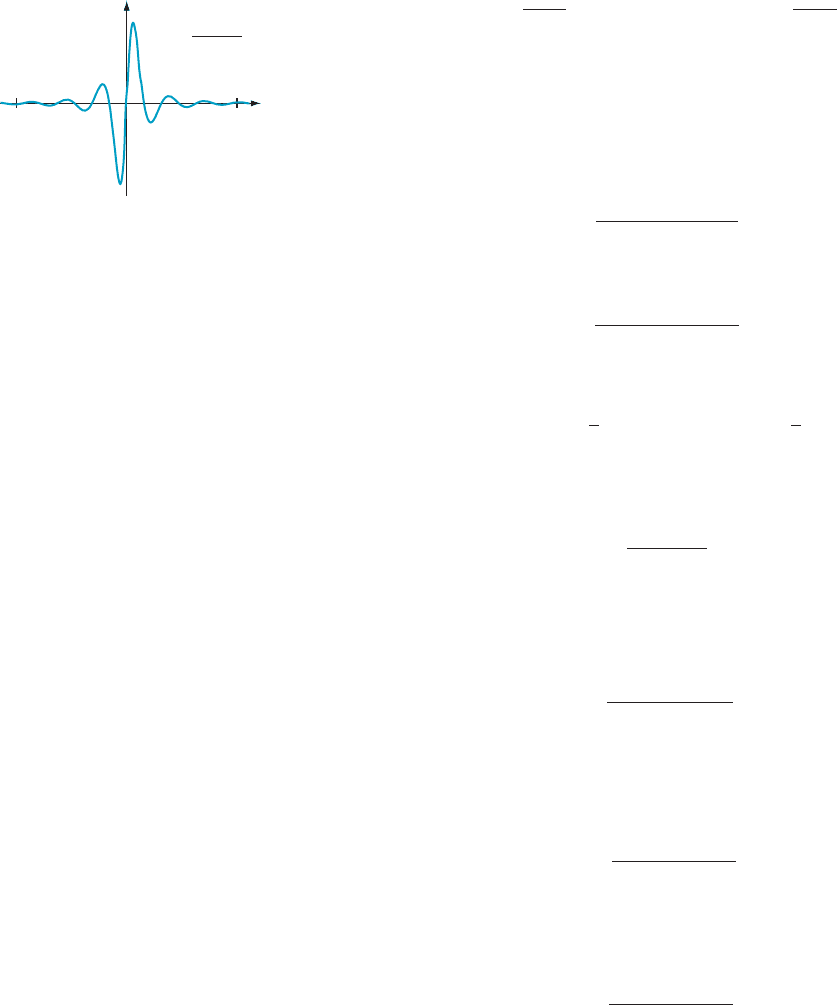
lim

x - 1N

gðxÞ5

0 1 1

5 0 and lim

x- 2N

gðxÞ5

0 1 1

5 0:

These limits show that the graph of g has the line y 5 0 as a left and a right

horizontal asymptote. Because the graph of g (x) oscillates about its asymptote, we

do not speak of y 5 0 as either an upper or a lower asymptote (see Figure 11).

⁄ EX

AMPLE 6 Determine all horizontal and vertical asymptotes for the

function

f ðxÞ5

2 1

1 12x

1 18x

Solution First,

if we divide the numerator and denominator by x

, we obtain

f ðxÞ5

7 2 1=x

2 1 12=x 1 18=x

It is then clear that

lim

x - 1N

f ðxÞ5

and lim

x- 2N

f ðxÞ5

Therefore f has the line y 5 7/2 as a horizontal asymptote.

For vertical asymptotes, we factor the denominator of f (x):

f ðxÞ5

2 1

2xðx13Þ

We notice that f is continuous except at 0 and 2 3. When x is close to and on either

side of 23, 7x

2 1 is negative, 2x is negative, and (x 1 3)

is positive and arbitrarily

small. It follows that

lim

x- 23

f ðxÞ5 lim

ð2Þ

ð2Þðsmall 1Þ

51N:

Therefore the line x523 is an upward vertical asymptote.

Also, when x is just to the left of 0, 7x

2 1 is negative, 2x is negative and

arbitrarily small in absolute value, and ðx13Þ

is positive. Therefor e

lim

x-0

f ðxÞ5 lim

ð2Þ

ðsmall 2Þð1Þ

51N:

Similarly, when x is just to the right of 0, 7x

2 1 is negative, 2x is positive and

arbitrarily small, and ðx 1 3Þ

is positive. Thus

lim

x-0

f ðxÞ5 lim

ð2Þ

ðsmall 1Þð1Þ

52N:

We conclude that the line x 5 0 is a vertical asymptote for f. Notice that the

asymptotic behavior on the left of 0 is different from that on the right of 0: On the

left, the graph goes up; on the right, it goes down. The graph of f in Figure 12

exhibits the vertical and horizontal asymptotes that we have found.

g(x) 

sin(2x)

1  x

1010

m Figure 11

2.4 Inﬁnite Limits and Asymptotes 123

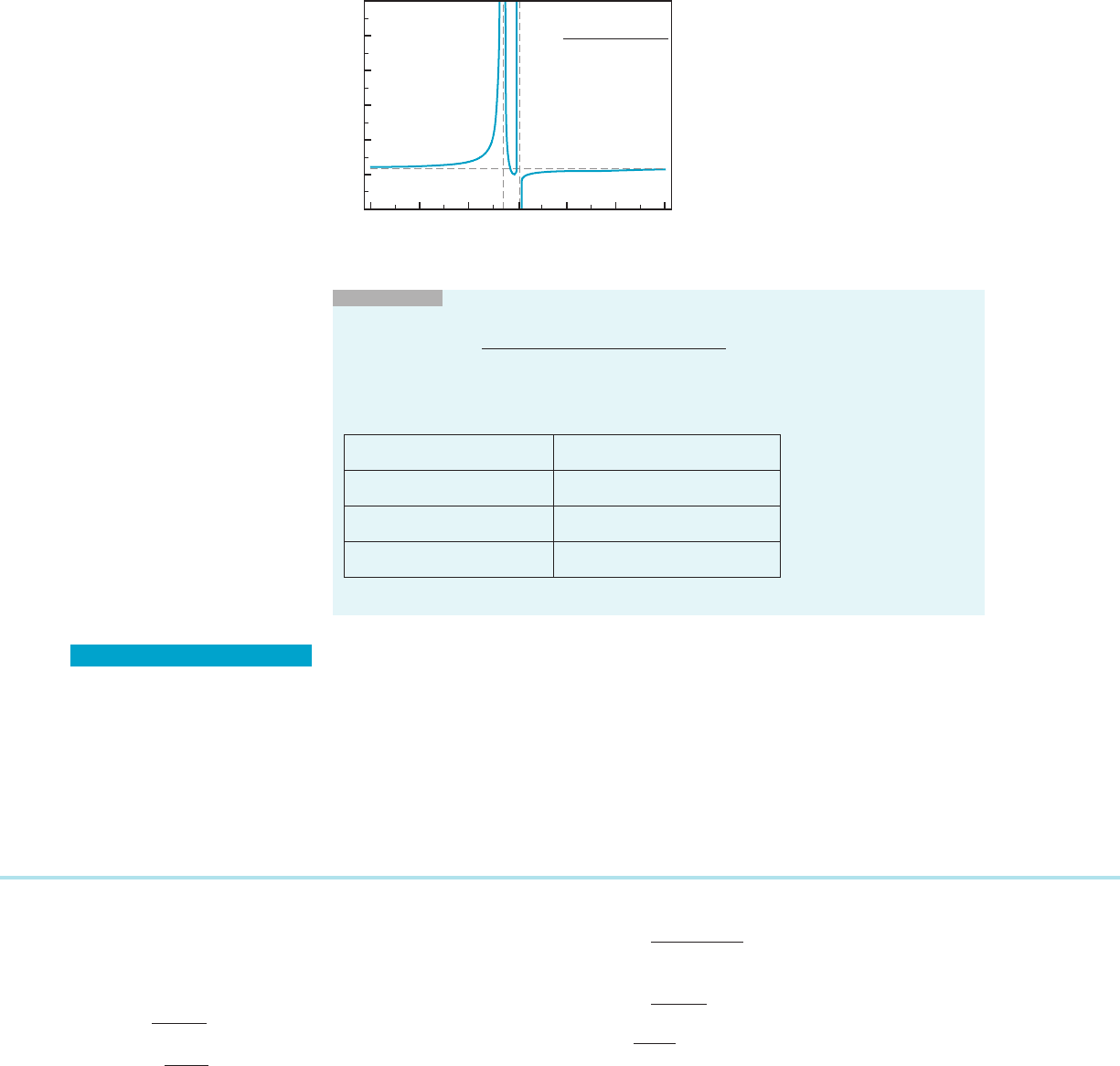
INSIGHT

When we seek horizontal asymptotes of a rational function

1 a

n21

1 1 a

x 1 a

1 b

m21

1 1 b

x 1 b

ða

; b

6¼ 0Þ;

it is useful to divide each term by x

. The resulting expression can be easily analyzed for

asymptotes. The result is shown in Table 1.

Comparison of Degrees Horizontal Asymptotes

n . m No asymptotes

n 5 m

y 5 a

as x-6N

n , my5 0asx-6N

Table 1

QUICK QUIZ

1. True or false: If f and g are continuous functions, and lim

x-c

gðxÞ5 0, then y 5 c

is a vertical asymptote for f/g.

2. True or false: If n and m are positive integers, and (x

1 1)/(x

1 2) does not

have a horizontal asymptote, then n . m .

3. Does the function f (x) 5 sin (x ) have either horizontal or vertical asymptotes?

4. What are the asymptotes for g( x ) 5 (x

2 5)/(2x

2 8)?

Answers

1. False 2. True 3. Neither 4. x 522, x 5 2, y 5 1/2

100

20

03102030 302010

f(x) 

 1

 12x

 18x

y  72

m Figure 12

EXERCISES

Problems for Practice

c In Exercises 1220, determine whether the given limit

exists. If it does exist, then compute it. b

1. lim

x-6

ðx 2 6Þ

2. lim

x-2N

4x 2 7

3. lim

x -1N

1 3x 2 92

2 7x

1 44

4. lim

x-211

ðx11Þ

5. lim

x -1N

x 1

ﬃﬃﬃ

6. lim

x-π

sinðxÞ

124 Chapter 2 Limits