Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

where a

5 1 1 r

1 r

1 1 r

N21

; and b

5 r

2 1: Using Theorem 4b with

r 5 1=2, we see that lim

N-N

5 1=ð1 2 1=2Þ5 2. Using Theorem 1e with r 5 1=2,

Theorem 1a with α 5 1, and Theorem 2b, we see that lim

N-N

5 0 2 1 521. Now,

using Theorem 2a, we have

1 5 lim

N-N

5 lim

N-N

1 lim

N-N

5 2 1 ð21Þ5 1: ¥

INSIGHT

A discussion of Zeno’s paradoxes (to which Example 10 is related) may be

found in Genesis and Development in Chapter 1.

⁄ EXAMPLE 11 What rational number does the repeating decimal expan-

sion 0.999 . . . represent?

Solution The

number 0.999 . . . represents

lim

N-N



100

1000

1 1



lim

N-N



1 1

100

1 1

N21



1 2 1=10

Theorem 4b

5 1: ¥

A LOOK BACK AND A LOOK FORWARD c When we refer to an “inﬁnite sum”

1 a

1 ; we actually mean the limit lim

N-N

ða

1 a

1 1 a

Þ of a

ﬁnite sum with an increasing number of terms. Chapter 8 is devoted to a detailed

study of such sums.

Using Continuous

Functions to Calculate

Limits

Consider the sequence fcos(

Þg

n51

. Because the cosine is continuous, we know that

lim

x-0

cosðxÞ5 cosðlim

x-0

xÞ5 cosð0Þ5 1. We also know that lim

n-N

ð1=nÞ5 0.

We therefore expect that lim

n-N

cosð1=nÞ5 cos



lim

n-N

ð1=nÞ



5 cosð0Þ5 1. The

next theorem justiﬁes this calculation.

THEOREM 5

Let fb

n51

be a sequence that converges to a limit ‘. Suppose

that fb

g and ‘ are contained in the domain of a function f that is continuous at

‘. Then lim

n-N

f ðb

Þ5 f ðlim

n-N

Þ5 f ð‘ Þ:

Proof. Le

t ε be a positive number. Let a

5 f ðb

Þ. We are to show that

lim

n-N

5 f ð‘Þ: Because f is continuous at ‘, there is a positive number δ such

that jf ðxÞ 2 f ð‘Þj , ε for all x in the interval I 5 ½‘ 2 δ;‘1 δ. Because

lim

n-N

5 ‘, there is an integer N such that b

is in I for each n $ N. It follows that

2 f ð‘Þj5 jf ðb

Þ2 f ð‘Þj, ε

for all n $ N, which proves the asserted limit. ’

2.5 Limits of Sequences 135

⁄ EXAMPLE 12 Evaluate lim

n-N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4 1 3=n:

Solution We

set b

5 4 1 3=n and f ðtÞ5

ﬃﬃ

. Then we see from Theorems 1 and 2

that ‘ 5 lim

n-N

5 4. Because f is continuous on the interval ð0; NÞ, an interval

that contains fb

g and ‘, we may ap ply Theorem 5. We concl ude that

lim

n-N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4 1

5 lim

n-N

f ðb

Þ5 f ð lim

n-N

Þ5 f ð4Þ5

ﬃﬃﬃ

5 2:

Our next theorem uses the function t/ 1=t; which transforms the sequence of

positive integers to a sequence that converge s to 0 from the right.

THEOREM 6

If lim

x-0

f ðxÞ 5 ‘; and a

5 f ð1=nÞ, then lim

n-N

5 ‘.

⁄ EX

AMPLE 13 Calculate lim

n-N

n sinð1=nÞ.

Solution We

let

5 n sin





sinð1=nÞ

1=n

5 f





for f ðxÞ5 sinðxÞ=x. The ﬁrst of the two limi t formulas in line (2.2.5) states that

lim

x-0

f ðxÞ5 1. Theorem 6 therefore tells us that lim

n-N

5 lim

x-0

f ðxÞ5 1. ¥

QUICK QUIZ

1. True or false: If lim

n-N

5 0 then there is a tail of the sequence for which the

absolute value of every term is less than 1= 10

100

2. Evaluate lim

n-N

100=n

3. Express 0:777 ::: as a rational number.

4. True or false: If lim

n-N

5 ‘; then a

n11

is closer to ‘ than a

for all n.

Answers

1. True 2. 1 3. 7/9 4. False

EXERCISES

Problems for Practice

c In Exercises 1215, determine whether the sequence fa

converges. If it does, state the limit. b

1. a

5 n=ðn

1 1Þ

2. a

5 n 1 5

3. a

5 3n=ð2n 1 1Þ

4. a

5 3 2 ð21Þ

5. a

5 1=ðn 1 2Þ

6. a

5 1 2 1=n

7. a

5 cos ðnπÞ

8. a

5 sinðnπÞ

9. a

5 3

1 2

10. a

5 1=n 2 4

1=n

11. a

5 ð3n

2 5Þ=ð4n

1 5Þ

12. a

5 ðn

2 nÞ=ðn

1 nÞ

13. a

5 4 1

ð2nÞ

1 1

14. a

5 n

1=100

15. a

5 ð1=100Þ

1=n

c In Exercises 16238, calculate lim

n-N

. b

16. a

5 3 1 4=n

17. a

5 2

2 6

18. a

5 ðn 2 2n

Þ=ðn 1 n

19. a

5 ð4n

1 6n 1 3Þ=ð8n

1 3Þ

20. a

5 ð7n

1 6n

1 n

Þ=ð3n

1 11Þ

21. a



3 1





2 2



22. a

5 ð10

1 10

Þ=10

23. a

5 2

 n=ðn 1 4Þ

24. a

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4n 1 1

ﬃﬃﬃ

136 Chapter 2 Limits

25. a

5 ð2 2 ð1=2Þ

Þ=ð4 1 ð1=3Þ

26. a

5 8

1=n

1 1=8

27. a

5 ð2

2 3

Þ=ð3

1 4

28. a

cosð1=nÞ

2 1 cscð1=nÞ

29. a

5 2sinð1=nÞ1 3 cosð1=nÞ

30. a

5 5 tanðπ

1=n

Þ2 3tanðπ=nÞ

31. a

5 tanðπn=ð3n 1 1ÞÞ

32. a

5 cotðn

π=ð4n

2 3ÞÞ

33. a

5 n

=ð2n

11Þ

34. a

5 4n=

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 5n 1 2

35. a

5 tanðπ 2

1=n

36. a

5 cosðπ sec ðn=ðn

1 1ÞÞÞ

37. a

5 sin



πsin



πn

6n 1 2



38. a

5 ð12  7

2 5

Þ=ð4  7

1 9 2

c In each of Exercises 39244, use the Pinching Theorem to

evaluate

lim

n-N

. b

39. a

5 cosðnÞ=n

40. a

5 sinð2nÞ=2

41. a

5 2

=ð3  2

1 cosð2

ÞÞ

42. a

ðcosð3

Þ1 2  3

43. a

5 ð21Þ

n=ð5 1 6ð21Þ

nÞ

44. a

5 ð2n

1 ð21Þ

n 1 1Þ=n

c In Exercises 45248, evaluate the geometric series. b

45. 1 1 1=3 1 1=9 1 1=27 1 

46. 1 2 1=3 1 1=9 2 1=27 1 

47. 1 1 1=

ﬃﬃ

ﬃ

1 1=3 1 1=ð3

ﬃﬃﬃ

Þ1 

48. 1=5 1 1=25 1 1=125 1 1=625 1 

49. Express 1:11111111 ::: as a rational number.

50. Express 1:01010101 ::: as a rational number.

Further Theory and Practice

c In Exercises 51254, determine the value of the given limit.

Then verify your answer using the precise deﬁnition of

limit. b

51. lim

n-N

n 1 7

52. lim

n-N

1 1

53. lim

n-N

2n 1 3

n 1 5

54. lim

n-N

1 2

c In Exercises 55260, evaluate the given sum. b

55. 1=4 1 1=8 1 1=16 1 1=32 1 



56. 1=

ﬃﬃﬃ

1 1=2 1 1=ð2

ﬃﬃﬃ

Þ1 1=4 1 

57. 16=3 1 32=9 1 64=27 1 128=81 1 

58. 3:512121212 :::

59. 123:01232323 :::

60. α

=ð11α

1 α

=ð11α

1 α

=ð11α

1 

61. Find a divergent sequence fa

g such that fa

g is

convergent.

62. Prove that, if fa

n51

converges to a real number ‘, then

lim

n-N

ða

2 ‘Þ5 0.

63. Prove that, if fa

n51

converges to a real number ‘, then

lim

n-N

ða

2 a

n11

Þ5 0.

64. Suppose that fa

n51

and fb

n51

are sequences satisfy-

ing ja

2 b

j, 1=n for every n. Prove that either both

sequences converge to the same limit or both sequences

diverge.

65. Suppose that a

-‘ 6¼ 0. Show that lim

n-N

ða

n11

converges.

66. Let α be a positive real number. Set a

5 1 and

5 ðα 1 a

n21

Þ=2 for n . 1. Find a formula for jα 2 a

Prove that fa

g converges.

67. Suppose pðxÞ is a polynomial of degree m and qðxÞ is a

polynomial of degree n, and prove the following

assertions.

a. If m , n, then lim

j-N

pðjÞ

qðjÞ

5 0:

b. If m 5 n, then lim

j-N

pðjÞ

qðjÞ

where p

is the

leading coefﬁcient of p, and q

is the leading coefﬁ-

cient of q.

c. If m . n, then lim

j-N

pðjÞ

qðjÞ

5 signum





68. If p is a polynomial, show that lim

j-N

pðj 1 1Þ

qðjÞ

5 1.

69. Many doubly indexed sequences fa

n;m

g arise in mathe-

matics. Often we need to know if

lim

n-N

lim

m-N

n; m

5 lim

m-N

lim

n-N

n; m

Show that this equality can be false by considering

n; m

5 n=ðn 1 mÞ:

70. Suppose that s is a ﬁxed positive number. Calculate

lim

n-N



s 1 2s 1 3s 1 1 ns



Calculator/Computer Exercises

c There are many sequences with convergence properties

that are not obvious. The sequences in Exercises 712 75

converge, but it is quite tricky to determine what the limit is

and

to prove the answer. Approximate the limit to four

decimal places. State what value of n you are using to

approximate the limit. b

71. lim

n-N

n: sinð1=nÞ

72. lim

n-N



1 2 cosð1=nÞ



73. lim

n-N

1=n

74. lim

x-N

ð121=nÞ

75. lim

n-N

ﬃﬃﬃ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃ

n11

ﬃﬃ

2.5 Limits of Sequences 137

76. Graph the function f ðxÞ 5 ð11xÞ

1=x

for 0 , x , 1: Focus

on the behavior of f (x) for small positive values of x by

replotting f in the window [0, 0.01, 2.705, 2.719]. What

does the limiting behavior of f (x)asx - 0

appear to

be? What does this behavior tell you about the limit of

the sequence fð111=nÞ

n51

77. Graph the function f ðxÞ5 x

for x . 0: What does the

limiting behavior of f ðxÞ as x-0

appear to be? What

does this behavior tell you about the limit of the sequence

1=n

n51

78. Here is an interesting way to use a sequence to solve a

quadratic equation: Consider the equation x

6x 1 5 5 0: Write x

5 6x 2 5, or x 5 6 2 5=x. For the x on

the right, substitute 6 2 5=x. The result is

x 5 6 2

6 2 5=x

Again, for the x on the right, substitute x 5 6 2 5=x. The

result is

x 5 6 2

6 2

6 2 5=x

This process, which we may continue indeﬁnitely, sug-

gests that x is the limit of the sequence

6; 6 2

; 6 2

6 2 5=6

; 6 2

6 2

6 2 5=6

;:::

This is called a continued fraction expansion. Compute

the ﬁrst 20 terms of this sequence. Do they seem to be

converging to something? Is the limit a root of the ori-

ginal quadratic equation? Can you discover the other

root in the same way?

2.6 Exponential Functions and Logarithms

We begin this section by extending our study of sequential limits. In the preceding

section, our method for demonstrating the convergence of a sequence was to

explicitly produce its limit. Now we will learn a theorem that establishes the con-

vergence of certain sequences even when their limits have not been identiﬁed. With

this theorem we are able to deﬁne the expression a

for any positive number a and

any real number x. By ﬁxing a 6¼ 1 and regarding x as a variable, we obtai n the

invertible function x/a

: This function, which is called the exponential function

with base a, and its inverse, the logarithm with base a, are the main focus of this

section. In some applications, particular choices of the base, such as a 5 2ora 5 10,

are convenient or traditional. In calculus, there is a particular base denoted by e

that is especially useful because it leads to formulas that are simpler than their

analogues with other bases.

The Monotone

Convergence Property

of the Real Numbers

Many sequences have the property that their terms get steadily larger. Other

sequences have terms that continuall y get smaller. Our next deﬁnition introduces

the terminology that describes such sequences.

DEFI NITION

A sequence fa

g is said to be:

’ increasing if a

, a

n11

for every n;

’ nondecreasing if a

# a

n11

for every n;

’ decre asing if a

. a

n11

for every n;

’ nonincreasing if a

$ a

n11

for every n.

These four types of sequences are said to be monotonic or monotone. Figure 1

shows an increasing sequence {a

} and a decreasing sequence {b

138 Chapter 2 Limits

A real number r with a nonterminating decimal expansion gives rise to a

nondecreasing sequence in a natural way. Consider r 5 1=3 5 0:3333 :::, for

example. If we set a

5 0:3, a

5 0:33, a

5 0:333, and so on, then we obtain a

sequence with each term greater than the preceding one. Notice that, even though

this sequence is increasing, its terms do not grow arbitrarily large. In fact, every

term in the sequence is less than 1/3. Our next deﬁnition describes sequences that

do not have arbitrarily large terms.

DEFINITION

A sequence fa

g is bounded if there is a real number U such that

j # U for all n. We refer to U as a bound for the sequence and say that fa

g is

bounded by U.

Notice that a sequence fa

n51

that is bounded by U is contained in the closed

interval ½2U; U. The converse is also true: If fa

n51

is contained in the interval

½α; β,thenfa

n51

is bounded by the maximum value of jαj and jβj.Ournext

theorem guarantees that a monotone, bounded sequence converges to a real number.

THEOREM 1

(Monotone Convergence Property). Suppose that fa

n51

monotone and bounded. Then fa

n51

converges to some real number ‘.IfI is a

closed interval containing fa

n51

, then ‘ belongs to I.

The Monotone Convergence Property is one way of expressing the com-

pleteness of the real number system. Because completeness is a vital requirement

for many of the important theorems about continuous functions, such as the

Intermediate and Extreme Value Theorems of Section 2.3, it is convenient to have

several formulations of completeness. Different, but equivalent, versions of the

completeness property are discussed in the Genesis & Development sections for

Chapters 1 and 2. Now we will study further applications of completeness (in the

form of the Monotone Convergence Property). Our ﬁrst example shows that every

decimal expansion corresponds to a real number.

⁄ EX

AMPLE 1 Suppose that m is a nonnegative integer and that fd

n51

is a

sequence of decimal digits. That is, each d

is an integer such that 0 # d

# 9.

Interpret the decimal expansion m:d

::: as the limit of a monotone, bounded

sequence.

Increasing sequence

n1

. . . . . .

n1

Decreasing sequence

. . . . . .

m Figure 1

2.6 Exponential Functions and Logarithms 139

Solution For every positive integer n, we truncate the decimal expansion after the

decimal place. In this way, we obtain a sequence f a

n51

with

5 m:d

:::d

. Our sequence is nondecreasing because a

n11

5 a

n11

=10

n11

$ a

. Also, fa

n51

is bounded by m 1 1. The Monotone Convergence

Property tells us that fa

n51

converges to some real number ‘. It is this number ‘

that the decimal expansion m:d

:::represents. ¥

Irrational Exponents Suppose that a is a positive number. If x is equal to an integer, then

5 a  a a

|ﬄﬄﬄﬄﬄ{zﬄﬄﬄﬄﬄ}

x factors

if x . 0, a

5 1ifx 5 0, and a

a  a a

|ﬄﬄﬄﬄﬄ{zﬄﬄﬄﬄﬄ}

jaj factors

if x , 0.

If a and b are positive bases, then elementary algebra shows that the laws of

exponents,

5 1; ð2:6:1Þ

5 a; ð2:6:2Þ

x1y

5 a

; ð2:6:3Þ

x2y

; ð2:6:4Þ

ða

5 a

; ð2:6:5Þ

ða  bÞ

5 a

 b

ð2:6:6Þ

hold for all integers x and y. These laws guide us in extending the deﬁnition of a

any rational number x 5 p=q where p and q are integers with q . 0: The ﬁrst step is

to deﬁne a

1=q

to be the q

root

ﬃﬃﬃ

of a (so that equation (2.6.5) holds with x 5 1=q

and y 5 q). As a result, we have

p=q

5 ða

1=q

ﬃﬃﬃﬃﬃ

It again requires only elementary algebra to show that the exponent laws (2.6.1)

through (2.6.6) remain valid for rational values of x and y. Additionally, if x 6¼ 0,

then we have

5 b if a nd only if b

1=x

5 a: ð2:6:7Þ

The terminology that we introduce now to describe the order properties of

exponentials will be used frequently in later chapters.

DEFINITION

Suppose that the domain of a real-valued function f is a set S of

real numbers. We say that f is increasing if f (s) , f (t) for all s and t in S with

s , t. We say that f is decreasing if f (s) . f (t) for all s and t in S with s , t.

⁄ EX

AMPLE 2 Let a be a positive number not equal to 1. Use the laws of

exponents to show that the exponential function x/ a

with base a is an increasing

function on the set of rational numbers if a . 1 and a decreasing function if a , 1.

Solution For

now, the domain S of the expo nential function with base a is the set

of all rational numbers. Suppose that 1 , a.Ifq is a positive integer, then

140 Chapter 2 Limits

1 , a 5 ða

1=q

.Ifa

1=q

# 1 were true, then a, the product of q numbers less than or

equal to 1, would also be less than or equal to 1. We conclude that 1 , a

1=q

.Ifp is a

positive integer, then a

p=q

, which is equal to ða

1=q

, is the product of p numbers

greater than 1. It follows that 1 , ða

1=q

. That is, 1 , a

for any positive rational

number r 5 p=q. As a result, for ration al numbers s and t with s , t,wehave

1 , a

t2s

. On multiplying each side of this inequality by the positive quantity a

,we

obtain the inequality a

, a

 a

t2s

5 a

s1ðt2sÞ

5 a

. This inequality shows that an

exponential function with base greater than 1 is increasing. Now suppose that a , 1,

and set b 5 1=a. Because b . 1, the exponential function with base b is increasing

(by the ﬁrst part of this example). Thus b

, b

holds for rational numbers s and t

with s , t. It follows that a

5 1=b

. 1=b

5 a

. ¥

We must still address the problem of deﬁning a

for irrational values of x.

What, for example, does the expression 3

ﬃﬃ

mean?

We answer this question by approximating 3

ﬃﬃ

by numbers of the form 3

where x is a rational approximation of

ﬃﬃﬃ

. The better x approximates

ﬃﬃﬃ

, the

better 3

approximates 3

ﬃﬃ

. Let us see how this idea can be put into practice.

Because

ﬃﬃﬃ

5 1:41421356 :::is between the rational numbers 1:4 5 14=10

and 1:5 5 15=10, we see that 3

ﬃﬃ

must be between 3

14=10

5 4:655536 :::and

15=10

5 5:196152 :::: We narrow the range in which 3

ﬃﬃ

must lie by using bette r

rational approximations of

ﬃﬃﬃ

. Thus because

ﬃﬃﬃ

is between 1:41 5 141=100

and 1:42 5 14 2 = 100, we see that 3

ﬃﬃ

must be between 3

141=100

5 4:706965 ::: and

142=100

5 4:758961::::From these estimates, we infer that 3

ﬃﬃ

5 4:7 to one decimal

place. Continuing this process, we let x

be the rational number obtained by ter-

minating the decimal expansion of

ﬃﬃﬃ

after the n

decimal place. We also let

5 x

1 1=10

. Then 3

, 3

ﬃﬃ

, 3

for every positive integer n. In the following

table, we record our calculations for n # 8.

1 1.4 1.5 4.655536722 5.196152423

2 1.41 1.42 4.706965002 4.758961394

3 1.414 1.415 4.727695035 4.732891793

4 1.4142 1.4143 4.728733930 4.729253463

5 1.41421 1.41422 4.728785881 4.728837832

6 1.414214 1.414215 4.728806661 4.728811856

7 1.4142136 1.4142137 4.728804583 4.728805103

8 1.41421356 1.41421357 4.728804376 4.728804427

Because the number 3

ﬃﬃ

lies between the last two numbers of each line of the

table, we see that 3

ﬃﬃ

must equal 4.728804 to six decimal places. Furthermore,

we deduce that we can deﬁne 3

ﬃﬃ

precisely by passing to the limit.

In general, if a is any positive number, and x is any irrational number, then we

deﬁne a

5 lim

n-N

ð2:6:8Þ

2.6 Exponential Functions and Logarithms 141

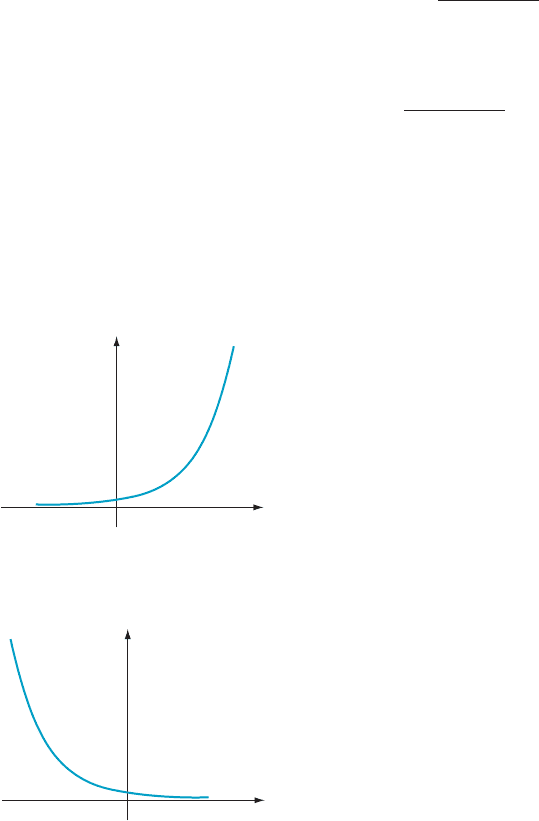
where fx

g is an increasing sequence of rational numbers such that lim

n-N

5 x.

Example 2 tells us that f a

g is a monotonic sequence. The Monotone Convergence

Property therefore assures us that the limit in formula (2.6.8) exists. Moreover, it is not

difﬁcult to show that this limit does not depend on the particular sequence fx

g that

approaches x. If it did, then the right side of formula (2.6.8) would not deﬁne a

in an

unambiguous way, and, as a result, formula (2.6.8) would not be an acceptable deﬁnition.

With a

extended to all real values of x by formula (2.6.8), the laws of expo-

nents recorded in lines (2.6.1) through (2.6.7) become valid for all real values of x

and y. In Chapter 5, we will use calculus to provide an alternative development of

irrational exponents. At that time we will prove the exponent laws.

⁄ EX

AMPLE 3 Simplify

π11

 π

ﬃﬃ

π21

 π

ﬃﬃ

and ð

ﬃﬃﬃ

 2

1=6

Solution We

calculate

π11

 π

ﬃﬃ

π21

 π

ﬃﬃ

5 3

ðπ11Þ2ðπ21Þ

 π

ð32

ﬃﬃ

Þ2ð12

ﬃﬃ

5 3

 π

5 9π

and



ﬃﬃ

ﬃ

 2

1=6



5 ðπ

1=3

ð2

1=6

5 π

ﬃﬃﬃ

Exponential and

Logarithmic Functions

We continue to let a denote a positive constant not equal to 1. Our present goal is

to describe the basic properties of the exponential functions with base a. For now,

we will be content to list the properties that are exhibited by their graphs.

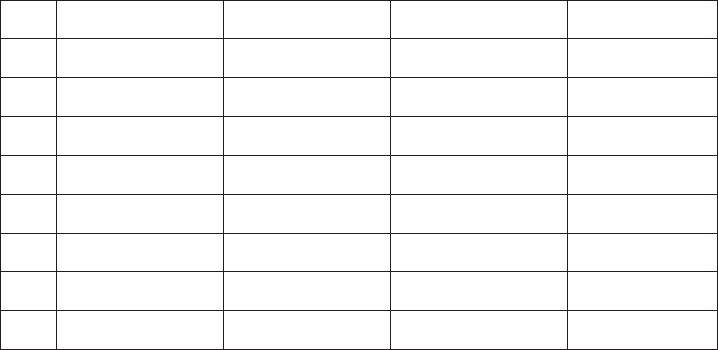
Figure 2 shows the graph of x/a

for a . 1. Notice that

lim

x - 2N

5 0 and lim

x-N

5 N for 1 , a:

Figure 3 shows the graph of x / a

for 0 , a , 1: Here we see that

lim

x - 2N

5 N and lim

x-N

5 0 for 0 , a , 1:

As the ﬁgures indicate, the exponential fun ction x / a

is continuous: For each c,

we have

lim

x-c

5 a

: ð2:6:9Þ

These observations, together with the Intermediate Value Theorem, allow us

to conclude that, for any positive base (not equal to 1), the image of an exponential

function is the set R

5 ð0; NÞ of positive real numbers.

The graphs of the exponential functions also exhibit another important property:

In Figures 2 and 3 we see that, for a . 1, the graph of y 5 a

is everywhere rising, and,

for 0 , a , 1, the graph of y 5 a

is everywhere falling. These properties are the

graphical representations of our observation in Example 2 that an exponential

function with base greater than 1 is increasing, and an exponential function with base

less than 1 is decreasing. (When we solved Example 2, the domain of x/a

was

limited to rational numbers. By continuity, the order relationships of the exponential

functions remain true when their domains are extended to all real numbers.)

y  a

m Figure 3 The graph of y 5 a

for 0 , a , 1

y  a

m Figure 2 The graph of y 5 a

for a . 1

142 Chapter 2 Limits

A function that is either increasing on its entire domain or decreasing on its

entire domain is necessarily one-to-one. Consequently, the exponential function

with base a is an invertible function with domain R and image R

. Its inverse is

called the logarithm with base a and is denoted by y/log

ðyÞ. The domain of a

logarithm function is R

; and the image is R. The inverse relationship between the

exponential function with base a and the logarithm with base a is expressed by

the following two ident ities:

log

ðyÞ

5 y for any positive number y and log

ða

Þ5 x for any real number x:

As with any pair of inverse functions, the graphs of y 5 a

and y 5 log

ðxÞ are

reﬂections of each other through the line y 5 x (see Figure s 4 and 5).

⁄ EX

AMPLE 4 Calculate log

ð81Þ.

Solution In

general, log

ðyÞ is the power to which we must raise 3 in order to

obtain y. For y 5 81; we have 3

5 81 and therefore log

ð81Þ5 4. ¥

Now we introduce some useful properties of logarithm functions.

THEOREM 2

Let a and b be positive numbers not equal to 1.Ifx . 0, and y . 0,

then

a. log

ð1Þ5 0;

b. log

ðaÞ5 1;

c. log

ðx  yÞ5 log

ðxÞ1 log

ðyÞ; and

d. log

ðx=yÞ5 log

ðxÞ2 log

ðyÞ:

e. For any exponent p; log

ðx

Þ5 p  log

ðxÞ;

f. log

ðxÞ5

log

ðxÞ

log

ðaÞ

; and

g. log

ðbÞ5

log

ðaÞ

Proof. Assertion

s a and b are just new ways of stating that a

5 1anda

5 a.

Properties c, d, and e can be derived from a corresponding property of the

exponential function with base a. As a representative example, we will show how to

deduce assertion c from equation (2.6.3). We let u 5 log

ðx  yÞ, s 5 log

ðxÞ,and

t 5 log

ðyÞ. It follows that a

5 x  y 5 a

5 a

s1t

. Because the exponential function

is one-to-one, we conclude that u 5 s 1 t, or log

ðx  yÞ5 log

ðxÞ1 log

ðyÞ.To

prove part f, we use part e with p 5 log

ðxÞ to see that

log

ðaÞlog

ðxÞ

5 b

log

ða

log

ðxÞ

5 a

log

ðxÞ

5 x;

which means that log

ðaÞlog

ðxÞ5 log

ðxÞ. Assertion g is the special case of

assertion f that results when x is taken to be b. ’

Equation (2.6.3) may be expressed in words as:

The

exponential of a sum is the product of the exponentials.

y  x

y  log

(x)

The graph of y  log

(x), 0  a  1

y  a

m Figure 5

y  log

(x)

y  a

y  x

m Figure 4

2.6 Exponential Functions and Logarithms 143

Similarly, Part c of Theorem 2 states the following:

The logarithm of a product is the sum of the logarithms.

We can see that these two statements really say the same thing if we keep in mind

the fact that logarithm and exponential are inverse operations.

Logarithms were invented because there was a practical application for a

function with property c of Theorem 2. In the late 16

century, multiplication was

a tedious process known only to scholars. John Napier (15501617) invented

logarithms to simplify multi plication. With tables that convert a positive number

u to log

ðuÞ and back, property c can be used to reduce the operation of multi-

plication to one of addition. The next example illustrates this idea.

⁄ EX

AMPLE 5 A table of logarithms base 10 contains the entries:

x log

(x)

6975 3.8435442119

7891 3.8971320434

55039725 7.7406762553

Use these entries to ﬁnd the product of 6975 and 7891.

Solution The

table tells us that 3.8435442119 and 3.8971320434 are the logarithms

base 10 of 6975 and 7891, respectively. The sum of these two logarithms is

7.7406762553. This is the logarithm of the number, 55039725, to its left. Thus

log

ð55039725Þ5 7 :7406762553 5 3:8435442119 1 3:8971320434

5 log

ð6975Þ1 log

ð7891Þ5 log

ð6975  7891Þ:

The number 55039725 is therefore the product of 6975 and 7891. (Logarithms were

widely used in this way from their ﬁrst publication in 1614 until the advent of hand-

held scientiﬁc calculators in the early 1970s.) The slide rule was a mechanical

implementation of this idea.

⁄ EXAMPLE 6 Simplify the expression

log

ð27Þ2 4 log

ð4Þ2 3 log

ð5

Þ:

Solution The

expression equals

log

ð3

Þ2 4 log

ð2

Þ2 3 log

ð5

Þ 5 3 log

ð3Þ2 4 



2 log

ð2Þ



2 3



2 log

ð5Þ



5 3  1 2 4  2  1 2 3  2  1

5211: ¥

144 Chapter 2 Limits