Blank L., Tarquin A. Engineering Economy (McGraw-Hill Series in Industrial Engineering and Management)
Подождите немного. Документ загружается.

SECTION 18.1
Determining Sensitivity to Parameter Variation
4.
Set
up the same PW relation as
in
part (a) at i = 15%. The PW results a
re
n
8
10
12
PW
$ 7,221
11
,5
11
13,145
5. Figure
1
8-
1 presents the plot of PW versus n. Since the PW measure is positive
for a
ll
values
of
n,
th
e decision to invest is not materially affected by the esti-
mated li
Je
.
The
PW
curve levels out above n = 10. This
in
se
ns
iti
vity to changes
in
cash
fl
ow
in
the distant future is a predictable observation, becau
se
the PI F
factor gets smaller as n increases.
Solution
by
Computer
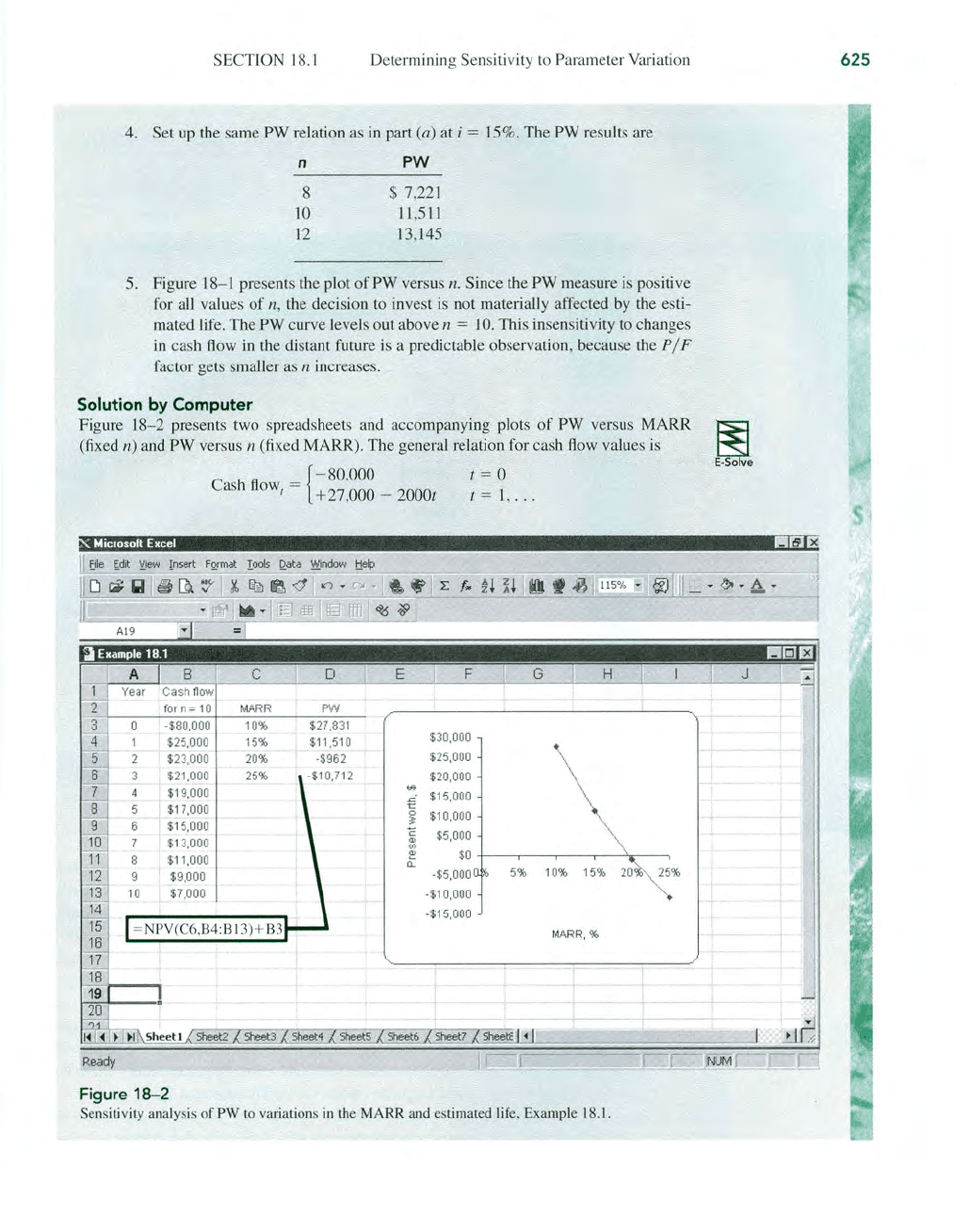
Figure
18
- 2 presents two spreadsheets a
nd
accompanying plots
of
PW versus
MARR
(fixed n) and
PW
versus n (fixed MARR).
The
general relation for cash flow values
is
{
- 80,0
00
t = 0
Cash
fl
ow, = +27,000 - 2000t t = 1,
...
m
E·Sol
ve
• Microsoft Excel
I!IrrJ
A19
~
Example 18.1
I!I~
13
B C
Cash
now
for
n = 10 M
ARR
PW
-$80.000
10%
$27,831
$25,000 15% $11,510
$30,000
$23,000
20%
-$962
$25,000
\
$21
,000 25%
$20,000
\
7 $19,000
.c
-
$1
5,000
8
$1
7,000
t
~
$1
0,
000
9
$15
,0
00
10
$1
3,
000
~
$
5,
000
11
0)
$0
$11
,0
00
ii:
2~
%
$9,000
-$5,000
0
",
5% 10% 15%
1
0
$7,000
-$10,000
-$15,000
= NPY(
C6
,B4:B 13) +
B3
MARR,%
S
he
et I Sheet2 Sheet3 Sheet4 SheetS Sheet6 Sheetl
Ready
Figure
18-2
Se
nsitiv
it
y analysis
of
PW
to variations
in
th
e
MARR
and estimated life, Example 18.1.
625
626
CHAPTER 18
Formalized Sensitivity Analysis and Expected
Valu
e Decisions
A19
iii E Kample
18
1
I!I~
f3
1
2
3
4
5
6
7
8
9
10
Ready
Figure
18-2
(Continue
d).
8 C
Cash
flow
for n
= 12
-$80,000
Li
f
e,
n
PW
$25,000
8
$7,222
$30,000
$23,000
10
$1
1,510
$25,000
•
$21,000
12
$13,146 $20,000
$19,000
...
+
~
$15,000
$17,000
t
~
0
$10,000
"
$15,000
c
$5,000
+
$1
3,000
~
$0
$11,000
0:
-$5,000
10
12
$9,000
$7,000
-$10,000
$5,000
-$15,000
$3,000
Life,
years
=
NPV(
15%,B$4:8 $15)+ 8 $3
SheetZ Sheet:l Sheet4 SheetS Sheet6 Sheet7
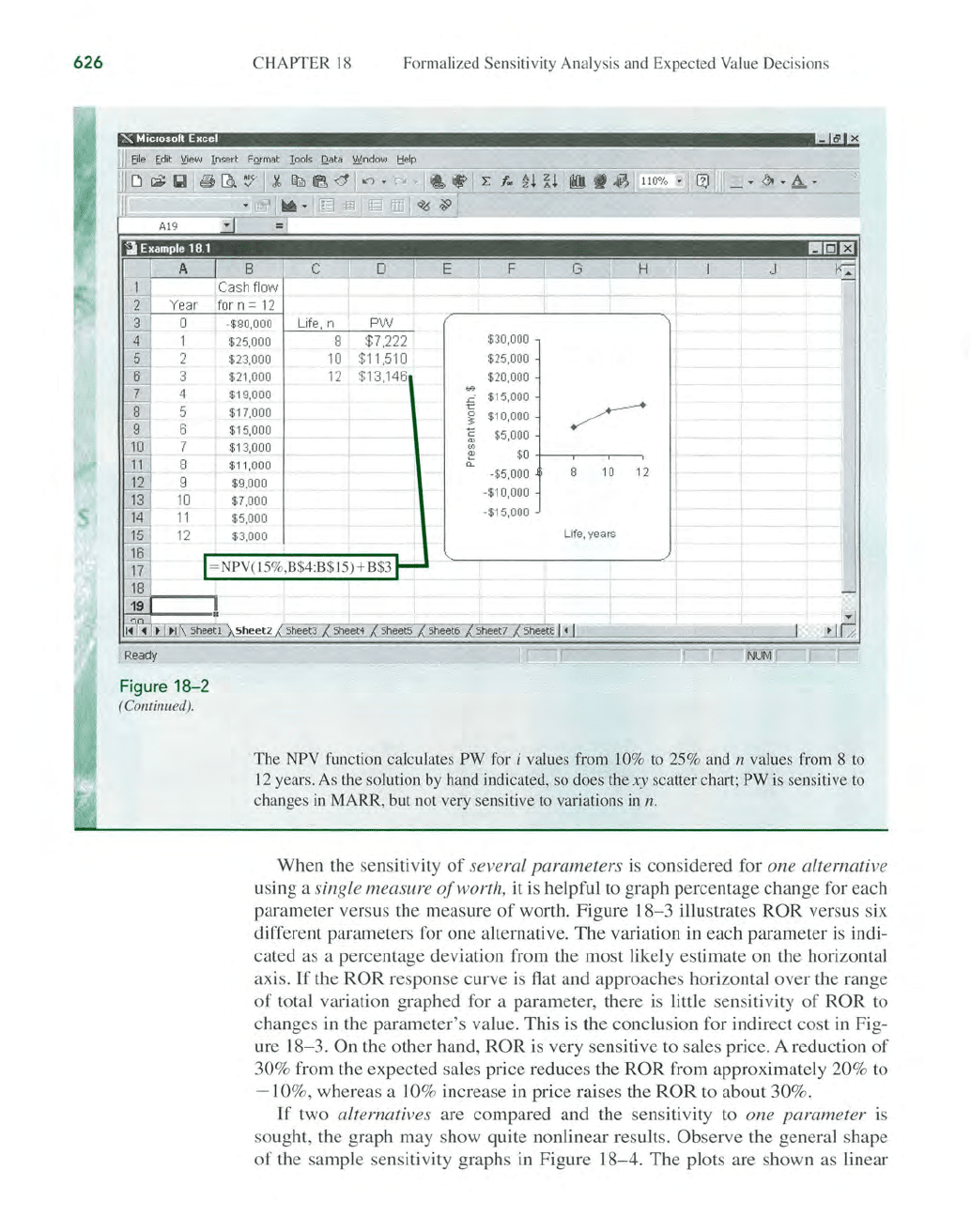
The
NPV function calculates
PW
for i values from 10% to 25% and n values from 8 to
12
years. As the solution by hand indicated, so does the
xy
scatter chart;
PW
is sensitive to
changes in MARR, but not very sensitive to variations in
n.
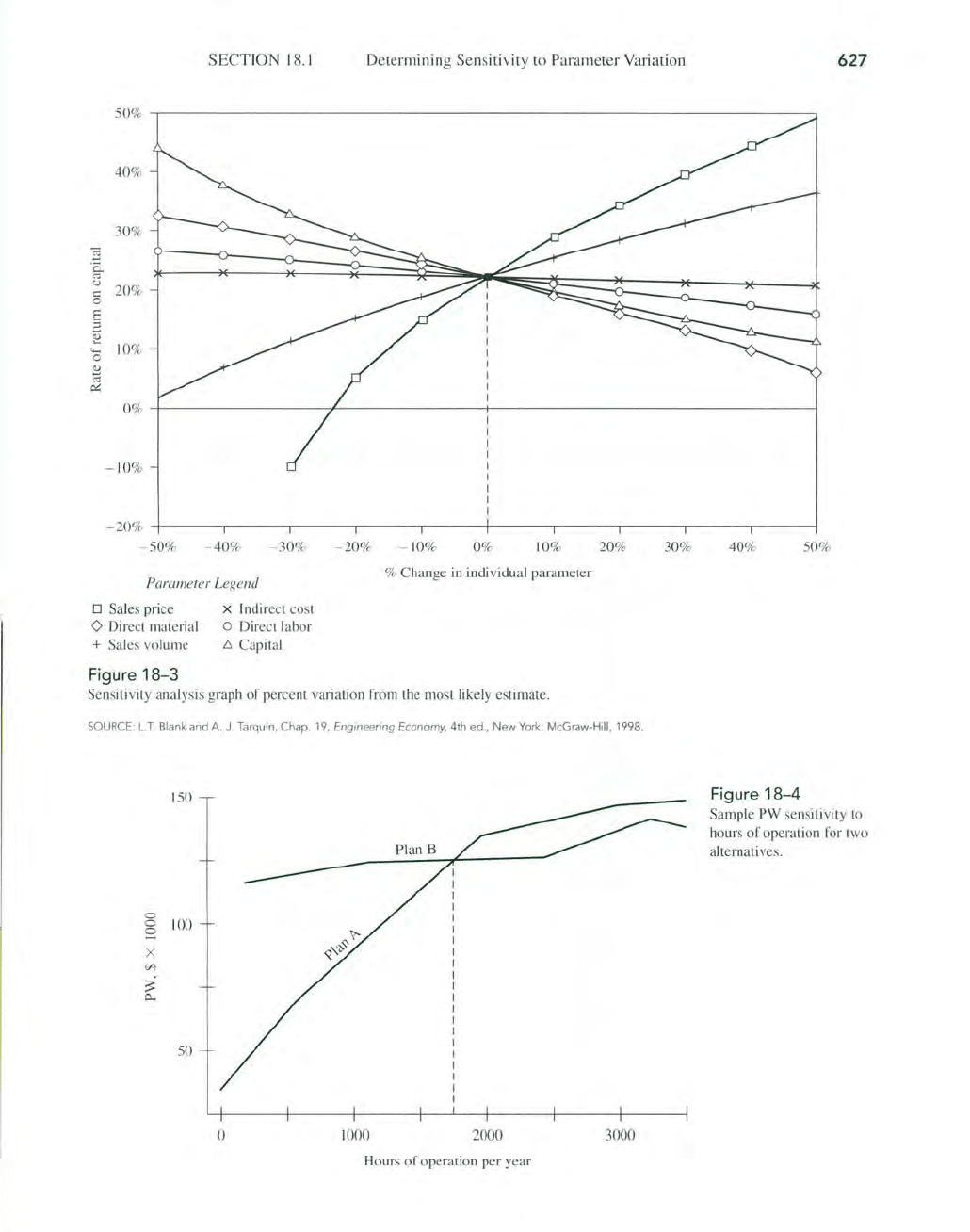
When the sensitivity
of
several parameters is considered for one alternative
us
in
g a single measure o.fworth, it is helpful to graph percentage change for each
parameter versus the measure
of
worth. Figure
18
- 3 illustrates
ROR
versus six
different parameters for one alternative.
The
variation in each parameter
is
indi-
cated as a percentage deviation from the most likely estimate on the horizontal
axi
s.
If
the
ROR
response curve is flat and approaches horizontal
over
the range
of
total variation graphed for a parameter, there is little sensitivity
of
ROR
to
changes
in
the parameter's va
lu
e, This is the conclusion for indirect cost
in
Fig-
ure
18-3, On the other hand,
ROR
is very sensitive to sales price. A reduction
of
30
% from the expected sales price reduces the
ROR
from approximately 20% to
- 10%, whereas a
10
% increase
in
price raises the
ROR
to about
30
%.
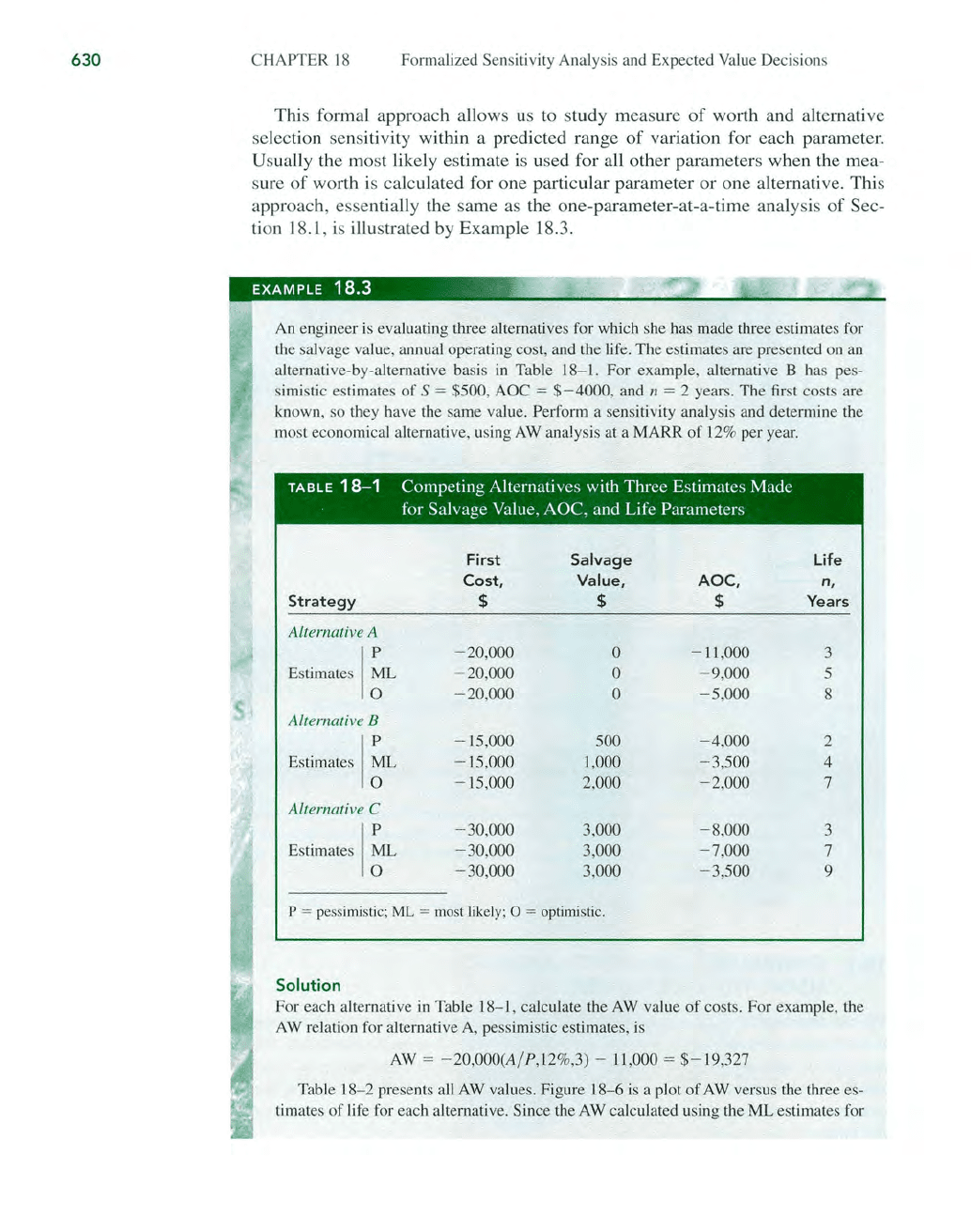
If
two alternatives are compared and the sensitivity to one parameter is
sought, the graph may show quite nonlinear result
s.
Ob
serve the general shape
of
the sample sens
iti
vity graphs
in
Figure
18-4.
The
plots are shown as linear
SECTION 1
8.
I
Determining
Sensitivity to
Parameter
Variation
627
50%
40%
30%
"§
'5.
'"
u
20%
25
<=
3
'§
<....
10%
0
E
'"
c.::
0%
- 10%
- 20%
~------.-------.------.-------.------~------.-------.-------.------.------~
- 50% - 40%
-3
0%
Parall1eler Legend
o Sales pri
ce
<>
Dir
ec
t material
+ Sales volume
Figure
18-3
x Indirect
cos
t
o Direct labor
'"
Capital
-20%
-
10
% 0%
10
%
%
Change
in
individual parameter
Sensitiv
it
y analysis graph
of
per
ce
nt variation
fr
om the most likely estimate.
20%
SOURCE:
L.T.
Btank
and
A. J. Tarquin, Chap. 19, EngIneering Economy, 4th ed.,
New
York: McGraw-Hili, 1998.
150
o
8 100
X
50
o 1000 2000 3000
Hours
of
operation per year
30%
40%
50%
Figure
18-4
Sa
mple PW sensitivity to
hours
of
operation for two
alternatives.

628
CHAPTER IS
Formalized Sensitivity Analysis and Expected Value Decisions
segments between specific computation points. The graph indicates that the PW
of
each plan
is
a nonlinear function
of
hours
of
operation. Plan A is very sensitive
in the range
of
0 to 2000 hours, but it
is
comparatively insensitive above 2000
hours. Plan B
is
more attractive due to its relative insensitivity. The breakeven
point is at about
1750 hours per year. It may be necessary to plot the measure
of
worth at intermediate points to better understand the nature
of
the sensitivity.
EXAMPLE
18.2
"b
1!l
E·
Solve
Columbus, Ohio needs to resurface a 3-kilometer stretch
of
highway. Knobel Construction
has proposed two methods
of
resurfacing. The first
is
a concrete surface for a cost
of
$1.5
million and
an
annual maintenance
of
$10,000.
The seco
nd
method is an asphalt covering with a first cost
of
$1 million and a yearly
maintenance
of
$50,000. However, Knobel requests that every third year the asphalt high-
way be touched up at a cost
of
$75,000.
The city uses the interest rate on bonds, 6% on its last bond issue,
as
the discount rate.
(a) Determjne the breakeven number
of
years
of
the two methods.
If
the city expects
an
in
-
terstate to replace this stretch
of
highway
in
10 years, which method should be selected?
(b)
If
the touch-up cost increases by $5000 per kilometer every 3 years, is the decision sen-
sitive to this increase?
Solution
by
Computer
(a) Use PW analysis to determine the breakeven n value.
PW
of
concrete = PW
of
asphalt
- 1,500,000 -
1O
,000(P / A,6
%,
n) = - 1,000,000 - 50,000(P / A,6
%,
n)
-
75
,000[
f(
P/ F,6
%,
j)]
where j =
3,
6, 9,
..
. , n. The relation can be rewritten to reflect the incremental
cash flows.
- 500,000 + 40,000(P/ A,6%,n) + 75,000[
f(
P/ F,6
%,
j)]
= 0 [IS.
I]
The breakeven n value can be determined
by
hand solution by increasing
It
until
Equation
[IS.l]
switches from negative to positive PW values. Alternatively, a
spreadsheet solution using the
NPV function can
find
the breakeven n value (Fig-
ure
IS
- 5). The NPV functions
in
column C are the same each year, except that the
cash flows are extended
I year for each present worth calculation. At approximately
n
= 11.4 years (between cells C15 and
CI6),
concrete and asphalt resurfacing break
even economically.
Since the road is needed for
10
more years, the extra cost
of
con-
crete is not justified; select tbe asphalt alternative.
(b) The total touch-up cost will increase
by
$1
5,000 every 3 years. Equation [IS.
1]
is now
- 500,000 + 40,000(P/A,6%,n) + [75,000 +
15,000e
~
3)]
[f
(P/F
,6%,j)]
=0

SECTION IS.2 Forma
li
zed Sensitivity Analysis Using Three Estimates
"
MIcro
soft Excel · Example 10.2
I!lIriJEJ
cash flow n ears
cash
flo
w
n
ears
$
(SOD
,000
) $ (
500
,
000)
1 $
40
,
000
$
(4
62
,2
64
) $
40
,
000
.\
462,264)
+
2
$
40,
000
$ (426,664) $
40
,
000
_ (
!26
,
664
)
3
$
11
5,0
00
$
(33
0,
108
) $
115,00
0
@
108
1.
---t-
4 $ 40
,000
$
(29
8,4
24)
$-
40
,
000
(2
98,424
)
5
$
40
,
000
$
(2
68
,534) $
40
,
000
(268,534)
6
$
115,000
$
(18
7
,464
) $ 130,
000
(
176,889)
J
___
7 $
40,000
$
(
16
0
,861)
$
40,000
$
(150,287)
8 $
40,000
,1
$
(1
3
5,765)
J
40,000
r $
_ i
125,190
h
9
I $
115,000
$
(F.i7,6%)
L
145,000
$
(39,365)
=NPV(6%,$D$5:$D14)+ $D$4
10
$
40,000
$
(45,361)
J
40,000
t $
(17,029)
11
1$
40,000
T $
(24
,;'
.!l2)
.
L
.
40,000
$
_.
~,O!2
r
=NPV(6%,$D$5:$D15) + $D$4
12
$
115,600'
I $
32,862
$
-
160,000
$
83,527
~t=--
~
.
~
.
13
$
40,0'00
$
51,616
$
40,0'00
$
JQ2,311
14
$
40,000
$ 69
,308
$
40,000
$
120,003
L
15
$ 115
,000
$
11
7,
29
3 $
175
,
000
$ f93,024 1
----r-
16
$
40
,
000
$
1
33,
039
$
40
,
000
$
208,770
= NPV(6%,$B$5
:$
B
15
)+
$B$4
-i
I
Sheet!
Sheet2 Sheet3
Figure
18-5
Sensitivity
of
th
e breakeven point between two alternatives using PW analysis, Example 18.2.
Now the breakeven n va
lu
e
is
between
10
and
11
years-lO.S
years using linear in-
terpolation (Figure
IS
- 5, cells E14 and
El
5). The decision has become marginal for
asphalt, since
th
e interstate
is
planned for
10
years hence.
Noneconomic considerations may be used to determine if asphalt is still the
bet-
ter alternative. One conclusion is that the asphalt decision becomes more question-
able as the asphalt alternative maintenance costs increase; that is, the PW value is
sensitive
to
increasing touch-up costs.
18.2
FORMALIZED SENSITIVITY ANALYSIS
USING
THREE ESTIMATES
We
can thoroughly examine the economic advantages and disadvantages among
two or more alternatives by borrowing from the field
of
project scheduling the
co
nc
ept
of
making three estimates for each parameter: a pessimistic, a most
likely, and an optimistic estimate,
Depending upon the nature
of
a parameter, the
pessimistic estimate may be the lowest value (alternative life is an example) or
the largest value
(s
uch
as
asset first cost).
j
629
630
CHAPTER 18 Formalized Sensitivity
An
alysis and Expected
Va
lu
e Decisions
This formal approach a
ll
ows us to study measure
of
wor
th and alternative
selection sensitivity within a predicted range
of
variation for each parameter.
Usually the most likely estimate is used for
all
other parameters when the mea-
sllre
of
worth
is
calculated for one particular parameter
or
one
alternative. This
approach, essentially the same as the
one
-par
ame
t
er
-at-a-time analysis
of
Sec-
tion 18.1, is illustrated by
Examp
le 18.3.
EXAMPLE
18
.3
An en
gi
neer is evaluating three alternatives for which she has made three
est
im
ates for
the salvage va
lu
e, annual opera
tin
g cost, and the lif
e.
The estimates are presented on
an
alternative-by-alternative basis
in
Table 18-1. For example, alterna
ti
ve B has pes-
simistic estimates
of
S = $500, AOC = $- 4000, and n = 2 years. The first costs are
known, so they have the same value.
Perf
orm a sensitivi
ty
anal
ys
is a
nd
determine the
most economical alternative, llsing
AW
analysis at a MARR
of
12% per year.
TABLE 18-1 Competing Alternatives wi
th
Three Estimates Made
for Salvage
Va
l
ue
, AOC, and Life Parameters
First Salvage
Cost, Value,
ADC,
Strategy $
$ $
Alternative A
Estimates
I h
L
-20,000
0
-
11
,000
-20
,000
0
-9
,000
- 20,000
0
-5,000
Alternative B
Est
im
ates I h
L
- [5,000
500
- 4,000
-1
5,000
1,000
- 3,500
- 15,000
2,000
-2,000
Alternative C
Estimates I
~L
- 30,000
3,000
- 8,000
- 30,000
3,000
-7,000
-30
,000 3,000
-3
,500
P = pe
ss
imistic;
ML
= most likel
y;
0 = optimistic.
Solution
Life
n,
Years
3
5
8
2
4
7
3
7
9
For each alterna
ti
ve
in
Table
18
- 1, calc
ul
ate the
AW
va
lu
e
of
costs. For example, the
AW
relation for alternative
A,
pessimistic estimates, is
AW
= - 20,000(A/P,12%,3) - 11,000 =
$-
19
,327
Table 18- 2 presents all
AW
values. Figure
18
- 6
is
a plot
of
AW
versus
th
e three es-
timates
of
li
fe
for each a
lt
e
rn
a
ti
ve. Since the AW calculated using the
ML
estimates
fo
r
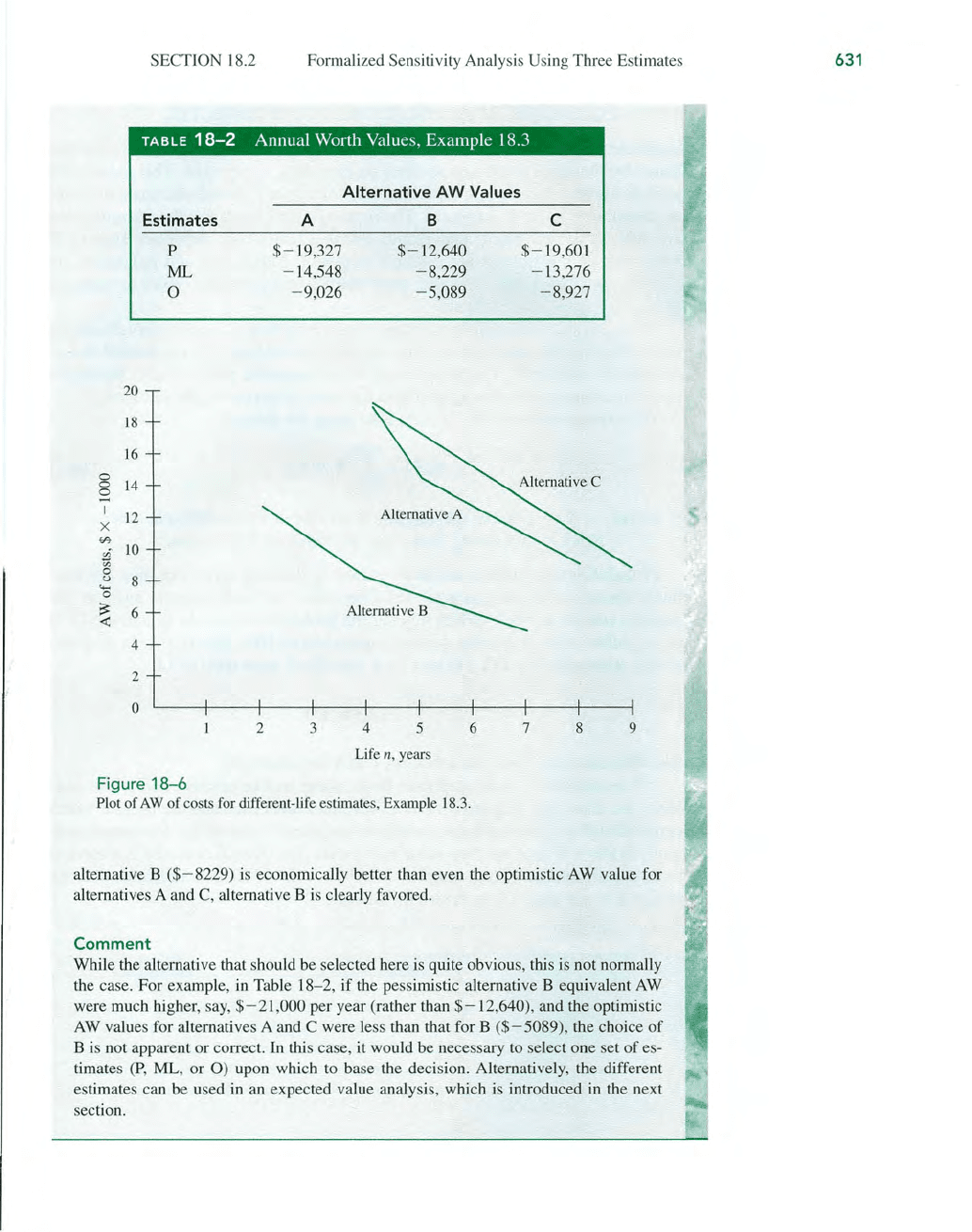
SECTION 18.2 Formalized
Se
nsitivity Analysis Using
Three
Estimates
TABLE
18-2
Annual Worth Values. Example 18.3
Alternative
AW
Values
Estimates A
B C
P
$-
19
,3
27
$- 12,640 $- 19,601
ML
-
14
,548 - 8,229
-13,27
6
0
-9
,026 - 5,089
-8,
9
27
20
18
16
0
0
14
S
I
12
x
""
'"
10
'"
0
u
8
'-
0
~
6
«
4
2
0
2
3
4
5 6
7
8 9
Lif
e n, years
Figure
18-6
Plot
of
AW
of
costs for different-life estimates, Example 18.3.
alternative B
($-8229)
is economically better than even the optimistic AW value for
alternatives A and C, alternative B is clearly favored.
Comment
While the alternative that should be selected here
is
quite obvious, this is not normally
the case.
For
example,
in
Table
18
-2,
if
the pessintistic alternative B equivalent
AW
were much higher, say,
$-21,000
per year (rather than
$-12
,640), and the optimistic
AW values for alternatives A and C were less than that for B
($-
5089), the choice
of
B is not apparent or correct. In this case, it would be necessary to select
one
set
of
es-
timates
(
P,
ML
,
or
0 ) upon which to ba
se
the decision. Alternatively, the different
estimates can be used
in
an expected value analysis, which is introduced
in
the next
section.
631

632
CHAPTER
18
Fo
rm
al
ized Sensitivity Analysis and Expected Value Decisions
18.3
ECONOMIC
VARIABILITY
AND
THE EXPECTED VALUE
Engineers and economic analysts usually deal with estimates about an uncertain
future by placing appropriate reliance on past data, if any exis
t.
This means
th
at
probability and samples are used. Actually the use
of
probabilistic ana
ly
sis is not
as
common
as might be expected. The reason for this
is
not that the computations
are difficult to perform
or
understand, but that rea
li
stic probabilities associated
with cash flow estimates are difficult to assign.
Ex
perience and
judgment
can
often be used in conjunction with probabilities and expected va
lu
es to eva
lu
ate
the desirability
of
an
alternative.
The
expected
va
lue can be interpreted as a long-run average observable if the
project is repeated many time
s.
Sin
ce
a particular alternative is evaluated
or
im-
pl
emented only once, a point estimate
of
the expected va
lu
e results.
However
,
even for a single occ
un
"e
nce, the expected value is a meaningful number.
Th
e expected value
E(X)
is computed using the rela
ti
on
i = m
E(X)
= I XiP(X;)
[18.2]
i= 1
where Xi = va
lu
e
of
the variable X for i from 1 to m different values
P
(X)
= probability that a spec
ifi
c value
of
X will occur
Probabilities are always correctly stated
in
decimal form, but they are rou-
tinely spoken
of
in
percentages and often referred to as chance, such as the
chances are
abou
t lO
%.
When placing the probability value in Equation [18.2]
or
any oth
er
relation, use the
de
cimal equivalent
of
10%, that is,
0.1
. In a
ll
prob-
ability statements the
P(X)
values for a variable X must total to 1.0.
i=
,n
I P
(X)
= 1.0
i=1
We will commonly
omit
the subscript i on X for simplicity.
If
X represents the estimated cash flows, some will be positive and others neg-
ative.
If
a cash flow sequence includes revenues and costs, and the present worth
at the
MARR
is calculated, the result is the expected value
of
the discounted cash
flows
E(
PW
).
If
the expected value is negative, the overall outcome
is
expected
to be a cash outflow. For example,
if
E(PW)
=
$-
1500, this indicates that the
proposal
is
n
ot
expected to return the MARR.
EXAMPLE 18.4
:~
A downtown hotel
is
offering a new se
rvi
ce for weekend travelers through its
bu
s
in
ess
and travel center. The manager estimates that for a typical weekend, there
is
a 50%
chance
of
having a net cash flow
of
$5000 and a 35% chance
of
$10,000. He also esti-
mates there is a small chance- 5
%-
of
no
cash
flow
and a 10% chance
of
a loss of
$5
00
, w
hi
ch
is
th
e estimated extra personnel a
nd
utility costs to offer
th
e service. De-
termine the expected n
et
cash flo
w.

SECTION 18.4 Expected
Va
lu
e Computa
ti
ons for Alterna
ti
ves
Solution
Let X be the net
ca
sh
fl
ow
in
do
ll
ars, a
nd
l
et
P(X
) represent
th
e associated probabilities.
Using Equation
[1
8.2],
E(X ) = 5000(0.5) + 10,000(0.35) + 0(0.05) - 500(0. 1) = $5950
Although the "no cash flow" possi
bil
i
ty
does not increase or decrease E(X),
it
is included
because it makes the probability values sum to
1.0 and
it
makes the computa
ti
on complete.
18.4
EXPECTED VALUE COMPUTATIONS FOR
AL
TERNATIVES
The expected va
lu
e c
omput
ation E(X ) is utilized
in
a variety
of
wa
ys. Two ways
ar
e:
(I) to prepare informa
ti
on for incorporation into a more
comp
lete engineering
economy analysis and (2) to eva
lu
ate the expected viability
of
a fully form
ul
ated
alterna
ti
ve. Example 18
.5
illustrates
th
e
fi
rst situation, and Example 18.6 deter-
mines the expected
PW when the cash flow se
ri
es and probabi
li
ties are estimated.
EXAMPLE
18
.5
An electric utility is experiencing a diffic
ul
t time obta
in
ing namral gas for electric gen-
eration. Fuels o
th
er than natural gas are purchased at an extra cost, which is transferred
to
th
e custome
r.
Total monthly fuel expenses are now averaging $7,750,000. An engi-
neer with
th
is city-owned utility has calculated the average revenue for
th
e past
24 months using thr
ee
fu
el-
mi
x si
tu
ation
s-g
as plentiful, less than 30% o
th
er fuels pur-
chased, a
nd
30% or more oth
er
fu
el
s.
Table
18-3
i
nd
icates the number
of
months that
each
fu
el-mix situation occurred. Can the uti
li
ty expect to meet future monthly ex-
penses based
on
dle 24 months
of
data, if a sim
il
ar fue
l-
mix patte
rn
continues?
Solution
TABLE
18-3
Revenue and Fuel-Mix Data, Example
18
.5
Fuel-
Mix
Situation
Gas plentiful
< 30% o
th
er
;:0:
30% odler
Months
in
Past
24
12
6
6
Average Revenue,
$
per
Month
5,270,000
7,850,000
12,130,000
Using
th
e 24 months
of
data, estimate a
pr
obabijjty for each fuel mix.
Fuel-
Mix
Situation
Gas plen
ti
ful
< 30% o
th
er
;:0:
30% o
th
er
Probability
of
Occurrence
1
2/24
= 0.50
6/ 24'= 0.25
6/ 24 = 0.25
633

634
CHAPTER 18
Fo
rm
a
li
zed Sensitivi
ty
Analysis a
nd
Expected Value Decisions
Let the variable
X represent average monthly revenue. Use Equation
[18
.2]
to
determine
expected revenue per month.
E(revenue)
= 5,270,000(0.50) + 7
,8
50,000(0.25) +
12
,130,000(0.25)
= $7,630,000
With expenses averaging
$7
,750,000, the average monthly revenue shortfa
ll
is
$120,000. To break even, other sources
of
revenue must be generated, or the additional
costs must be transferred to the customer.
EXAM PLE
18.6
<"~
Lite-Weight Wheelchair Company has a substantial investment in tubular steel bending
equipment. A new piece
of
equipment costs $5000 and h
as
a life
of
3 years. Estimated
cash
flow
s (Table 18-4) depend on economic conditions classified
as
receding, stable,
or expandin
g.
A probabili
ty
is
estimated that each
of
the economic conditions will pre-
vail during
th
e 3-year period. Apply expected value and PW analysis
to
determine if the
equipment should be purchased.
Use a MARR
of
15
% per year.
TABLE
18-4
Equipment Cash Flow and Probabi
li
ties, Example 18.6
Economic Condition
Receding Stable Expanding
Year (Prob.
= 0.2) (Prob. = 0.6)
(Prob.
= 0.2)
Annual
Cash
Flow Estimates, $
0
$-5
000
$-
5000
$-5
000
1 + 2500
+2000
+2000
2
+2
000
+2000
+3
000
3
+10
00
+2
000
+3
500
Solution
First determine the PW
of
the cash
flows
in
Table 18-4 for each economic condi-
tion, and
th
en calculate E(PW), using Equation [18.2]. Define subscripts R for re-
ceding economy,
S for stable, and E for expanding. The PW values for the three
scenarios are
PW
R
= - 5000 +
2500(P/F
,
15%,I)
+ 2000(P/F,15
%,
2) +
1000(P/F
,1
5%,3)
= - 5000 + 4344 =
$-6
56
PW
s
= - 5000 + 4566 =
$-43
4
PW £ = - 5000 + 6309 =
$+
1309
