Brewster H.D. Fluid Mechanics
Подождите немного. Документ загружается.


132
Basic Equations
of
Fluid Mechanics
a
• Modification
of
the mass
of
component A
-~pA(UA)jOV9tby
OXj
inflow and outflow
• Production
of
the chemical component A
r1)V
9t
by chemical reaction
Thus yields a mass balance:
apA
a
~ ~
-OV9t
=
--[PA(U
A
)JuV
9t
+rAuV
9t
at
aXj
and the equation for the mass conservation for the chemical component
A
of
a fluid results as:
.,
apA
a
-+-[PA(UA)d=rA
at
aXj
For a chemical component B, as a consequence
of
equal considerations:
apB
a
-+-[PB(UB)j]=rB
at
aXj
The addition
of
these equations yields:
ap +
a(pU
j
)
0
at
ax·
i.e. the total mass conservation
eq~ation
for a mixture
of
different
components is equal to the continuity equation for a fluid which consists
of
one chemical component only. By considering Fick's law
Qf
diffusion it can
be stated:
apA
~
. a
~
a(CAIC)]
:It
+:1
. (PAU,) = -
pDAB
a +rA
o
oX
,
ax· X·
I ' I
For P = const and
DAB
= const, one 0 tains:
=0
,--A--..
2
apA
aU
j
apA
a
PA
--+
PA
--+
U·
--
=
DAB
--
+
rA
..
at ax· I ax· ax·
d
·
f'·
I C I
or expresse
III
terms 0 concentratIOn, A
DCA
=
[aC
A
+U.
aCA]=D
a
2
c
A
+R
Dt at I
aXj
AB
axJ
A
with r
A
=A·
R
A
•

Chapter 5
Gas
Dynamics
Gas dynmaics is a sub-domain
of
fluid mechanics which deals with the
motion
of
gases at high velocities. The study
of
gases in motion. In general,
matter
exists in
any
of
three
states: solid, liquid,
or
gas. Liquids
are
incompressible under normal conditions; water
is
a typical example. In contrast,
gases are compressible fluids; that is, their density varies depending on the
pressure and temperature. The air surrounding a high-speed aircraft is an
example.
Gas dynamics can be treated in a variety
of
ways. One such way deals
with gases as a continuum. The structure
of
gases on the particle level is called
rarefied gas dynamics. Gases in motion are subject to certain fundamental
laws. These are the laws
of
the conservation
of
mass, momentum, and energy.
In the case
of
the dynamics
of
incompressible fluids, it is usually sufficient to
satisfy only the laws
of
conservation
of
mass and momentum. This distinction
constitutes the fundamental difference between high-speed gas dynamics and
hydrodynamics.
If
irreversibilities are involved, a fourth equation called the
entropy balance equation may be considered. Whereas mass, momentum, and
energy are conserved, the entropy is not. Real problems are irreversible; that
is, losses such as friction are involved. However, as a first approximation such
effects are generally not considered.
To understand why this is important, we must consider the structure
of
a
gas. Air, the medium
of
greatest interest to us, is a mixture
of
gases. It is
roughly 79% nitrogen, a gas composed
of
diatomic molecules, 20% Oxygen,
another diatomic gas, and 1 %
of
other gases such as Argon, Carbon di-oxide
etc. which do not significantly alter the properties
of
air.
At any temperature above absolute zero, the molecules
of
a gas are in
constant motion. The speed
of
this "random thermal motion" varies from
molecule to molecule, and instant to instant. The variation occurs through
collisions between molecules.
At
any given instant, one expects to find
molecules traveling at many different speeds and in all directions.
If
one finds
the mean velocity
of
all these molecules, one comes up with the mean velocity
of
the gas as a whole:
if
it is flowing, there is a finite mean velocity.
If
it is

134
Gas Dynamics
just contained
in
a stagnant chamber, the mean may be close to zero. However,
if
one finds the mean speed, i.e., ignore the directions, and
just
see how fast
things are moving, one gets a value which
is
proportional to the temperature.
In fact, what we call "temperature"
is
a measure
of
the kinetic energy
of
the
molecules. Thus, the greater the temperature, the greater the speed
of
random
thermal motion
of
molecules.
Pressure
is
the force, per unit area, felt on a surface due to the "momentum
flux" through the surface.
If
our surface
is
an imaginary one in a gas, then the
"momentum flux" is the rate at which molecules are carrying "momentum",
i.e., their own mass times their velocity, across the surface.
If
it is a solid
surface where we feel the pressure, this is due to the momentum transferred to
the surface, when the molecules collide with the surface and change direction.
Thus pressure
is
related to how fast the molecules are moving (the temperature),
how massive the molecules are (the molecular weight), and how many
molecules there are, per unit volume (number density, related to density).
The temperature and the type
of
gas determine the "speed
of
sound". The
speed
of
sound
is
the speed at which the smallest imaginable disturbances in
pressure, travel through an undisturbed medium.
It
is
a property
of
the medium.
For disturbances to propagate, molecules must collide with each other,
transferring momentum and kinetic energy. Thus, the speed
of
sound
is
roughly
equal to the mean speed
of
the molecules! In fact, the relation
is:
Speed
of
Sound = square root
of
(y RT) where y called the "ratio
of
specific heats"
of
the gas, and R
is
the "gas constant"
of
the gas. The gas
constant
is
obtained by dividing the Universal Gas Constant (8314 in SI units)
by the molecular weight
in
kilograms per kilogram-mole. Typically, in air at 0
deg. Celsius (273.2 deg. K), the speed
of
sound
is
roughly 340 meters per
second.
Gravitational forces and their influence on flows can be neglected here
for the most part. Considerations
of
the pressure differences to be expected
by gravitational forces in gas flows show that this
is
justified:
M =
-pgrj
= pg&-,
which can be determined for an ideal gas (P =
pRD
with the following relation:
M _
&-
~9
81~~
!!:.
ms K
[
2
1
p - g P ,
287T
287T
s2
m
2
K .
When inserting
T"" 293 K it can be
seenthat
the relative pressure changes
that depend on gravitation assume values around 1
% only when vertical
displacements
of
about
100
m occur. As gas-dynamic considerations are usually
restricted to installations
of
much smaller dimensions, it
is
justified to simplify
the flow-mechanical basic equations for considerations in gas dynamics by

Gas Dynamics
135
neglecting the gravitational forces. For many flow-mechanical considerations
it
is
permissible to regard gaseous fluids also as incompressible when the
occurring fluid velocities are small as compared to the sound velocity
of
the
fluid. This can be explained for a stagnation point flow by the following
consideration:
2
P
s
= P
00
+ g
L\2°O
with P = const
When the compressibility
of
a fluid is to be considered, e.g. for an ideal
gas
at
high flow velocities, for the stagnation pressure under adiabatic
conditions holds, where in the framework
of
the stream tube theory gasdynamic
considerations were carried out already:
or written as series expansion:
= P
[1+
Poo
U2+_1
(pooU~)2
+
...
]
P s
00
2P
00
2k
P
00 00
From this follows that for k =::
1,
4 and T
=::
293, there have to exist
velocities in the range
of
70 mls before stagnation pressures
of
incompressible
and compressible fluids differentiate by about 2% As gas dynamics is the
science
of
compressible fluid flows, it thus treats flows at high velocities where
the fluid compressibility has to be included into the considerations.
Such flows
are characterized by the Mach number
Ma" so that the compressibility
of
a
fluid is to be considered only onwards from:
U U
Ma =
-;=
~kRT
~0,2
As the sound velocity C
(T)
is given by the temperature field and for
=::
300K, velocities
of
C
=::
350mls
exist, gas-dynamic aspects have to be
considered with fluid flows only at high Reynolds numbers. Therefore it
is
permissible to neglect the viscosity term
in
the momentum equation. Thus the
basic equations
of
flow mechanics for gas-dynamic considerations can be stated
as shown below. In these equations the relations holding for ideal gases were
introduced for the internal energy:
e =
CaT
and
Co
= const:
Continuity equation
op
o(pUJ
a;+
8x.
= 0,
I
Momentum equation (j =
1,2,3)

136
Gas Dynamics
p[aU
j
+u
au
j
]
= _
ap
at
I
~'o
'
UA
I
ax;
Energy equation
pcv[or
+U
i
or]
= _pau
j
at
ax;
oXi '
where the
oenergy
equation) is given for adiabatic fluid flows. Together with
the state equation for ideal gases, a closed system
of
differential equations
exists which can be solved for given boundary conditions. Gas-dynamics
problems are thus solvable in principle.
The possible solutions require special considerations, however, the
appearance
of
high flow velocities is linked to specific phenomena which
differentiate gas dynamics sharply from other sub-domains
of
flow mechanics.
As the following considerations will show, the presence
of
high Mach
numbers,
Ma = U Ie, leads to the emergence
of
"discontinuity surfaces"
(compression shocks) in which the pressure (and other flow quantities)
experience a jump. This makes a special procedure necessary when solving
flow problems, as the employment
of
the differential form
of
the basic equations
usually requires that the quantities describing a flow are steady in the flow
area.
There
is
also the fact that when treating fluid flows at high Mach numbers,
processes occur that are linked to different time scales. These are the time
scales
ofthe
diffusion
~tDiff,
the convection
~teonv
and the sound propagation
MSound:
For
Meonv
~tDiff
it results:
M
U·L
Re
=
Diff
= c
c»
1
~teonv
v
i.e. during the time in which a flow covers a certain distance, the molecular
transport at high flow velocities manages only to overcome a negligible dis-
tance, i.e. at high Re-numbers the formation
of
thin boundary layers comes
about. The latter are neglected in the introducing considerations presented here.
From the point
of
view
of
characteristic times it results analogously for the
Mach number:
~teonv
U
c
Ma =
=-
~tSound
c
i.e. the Mach number shows how quickly flows proceed in fluids, relative to
the characteristic velocity
of
the propagation
of
small disturbances, i.e. the

Gas Dynamics
137
sound velocity c. c depends on the thermo-dynamic change
of
state and can
be stated as follows:
k =
c/c
v
= Relation
of
the heat capacities
c
=.J
kRT
R = Specific gas constant
T = Absolute temperature
This context between the sound velocity and the thermodynamical state
quantities pressure and density can be presented as follows: Considered
is
the
propagation
of
a small (i.e. isentropic) disturbance at the velocity c in a fluid
at rest.
This is a non-stationary process which by changing the reference system
(the observer moves together with the flow) can be modified into a stationary
problem, Now the momentum equation can be employed as a balance
of
forces
at a control volume around the disturbance:
F [P -
(P
+
dP)]
= pFc[(c + dU) -
c]
The equation gives the following relation:
-elP =
pcdU
For the mass conservation it can..be-stated:
"'"
~.....
--::
,~
pFc·
r
::
(r + dr)(c + dU)F
Storung
Fig. Propagation
of
a Disturbance in a Compressible Fluid
so that it holds:
Thus it also holds:
dU
dp =
-p-
c
dP
=c
2
=
(8P)
dp
8p ad
as no heat exchange
is
included in the present considerations.
The sound velocity is therefore a local quantity, i.e. it depends on the
locally existing pressure changes. With the local value
c(x
i
,
t) the local Mach
number can be computed at each point
of
a flow field
~(xi'
t), so that the
corresponding Mach number field can be assigned to the flow field, i.e.
Ma(xj>

138
Gas Dynamics
t.) This local Ma-number expresses essentially how quickly at each point
of
the flow field disturbances propagate relative to the existing flow velocity.
From a historic point
of
view it
is
interesting that Newton was the first
scientist to compute the sound velocity for gases, although on the assumption
of
an
isothermal process
in
which no temperature changes occur due to the
sound propagation. He thus obtained in his considerations:
c =
{P
=.J
RT
< c
Newton
{p-
Only a full century later Marquis de Laplace corrected the result
of
Newton's
computations by recognizing that the temperature fluctuations
produced by sound disturbances and also the temperature gradients connected
with them are very small. Laplace recognized that it
is
not possible to radiate
the
heat.
The
Jk
-correction
of
Newton's formula introduced by Laplace led
to the correct propagation velocity
of
sound waves
in
ideal gases:
c
= .JkRT
Attention is drawn once again to the fact that via this formula a sound
velocity field also
T
(Xi'
t) is assigned to each temperature field c(xi' t)
of
an
ideal gas.
MACH
LINES
AND
MACH
CONE
Fig. Propagation
of
Disturbances with Stationary Disturbance Source
When considering a disturbance emanating from a point source in the

Gas Dynamics
139
origin
of
a coordinate system, same will propagate radially at the velocity c
if
the point source does not carry out any motion, i.e. the surfaces
of
disturbance
of
the same phase represent spherical surfaces when the propagation takes
place in a field
of
constant temperature.
When there is on the other hand a temperature field with variations
of
temperature, these variations are reflected as deformations
of
the spherical
surfaces. The propagation takes place more rapidly
in
the direction
of
high
temperatures, as
is
predicted in equation. Possible temperature distributions
impair thus the symmetry
of
the propagation
of
sound waves.
When
one extends now
the
considerations
of
the
propagation
of
disturbances to moving disturbance sources
of
small dimensions, for U < c,
i.e.
Ma < 1 and U > c, i.e. Ma > 1 By moving the disturbance source at a
velocity
smaller
than the
propagation
velocity
of
the
disturbances
as
diagrammed in figure a propagation image
result~
which does not show any
more the
"symmetric propagation
of
the disturbances" will be obtained in the
propagation direction
of
the disturbance source, a concentration
of
the emitted
disturbance waves takes place, i.e. an observer standing
in
positivexcdirection
will register a frequency increase
of
the disturbance as compared to the starting
frequency
of
the disturbance source. In the opposite direction on the other
hand a frequency decrease takes place toward the emitted disturbance.
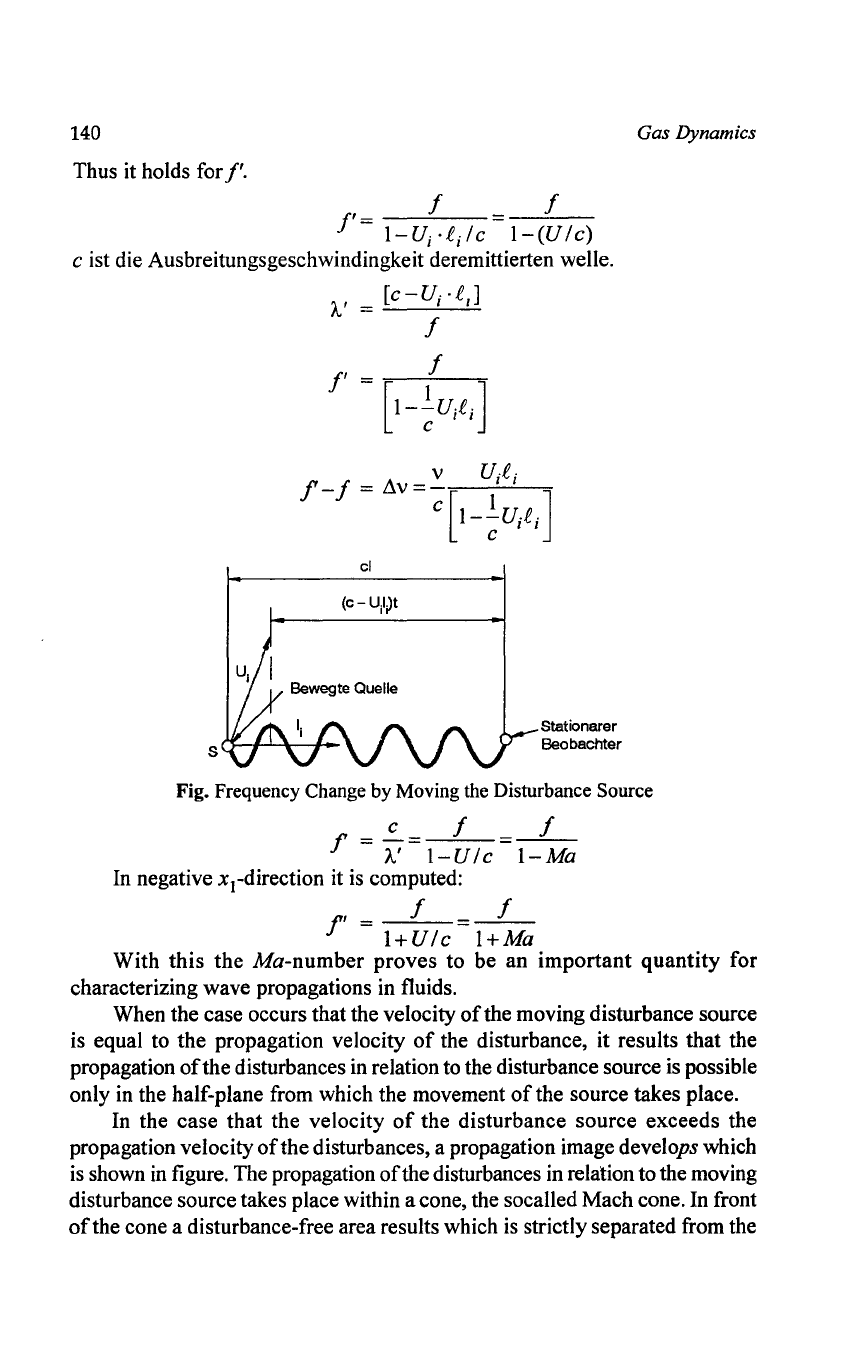
When one computes this frequency change for the frequency increase in
positive
xcdirection, it results according to figure for
Ma
<
1:
c(3~t)
/ c(2At)
c(3At)
c(2..it)
c(~t)
U<c
I c(..it) U
I
>c
-
(a) U < c "'" Ma < 1
(b) U < c "'" Ma > 1
Fig.
Propagation
of
disturbances
with
a
moved
disturbance
source
for
Ma < 1
and
Ma > 1
-
U(..it)
c-U·
·f·
(c-U)
A'
= I I or with U
j
•
C j = U where
A'
= and
fj
states the
unit vector in{he direction
of
propagation
(j=
frequent;,
of
the disturbance)
140
Thus it holds for
f'.
f
f'
=
---=---
=
I-U;
·C;le
I-(Ule)
f
e ist die Ausbreitungsgeschwindingkeit deremittierten welle.
S
[
e
-0..
C ]
A'
= I I
f
v
U·C·
f-f
=
~v=~[
l' I ]
I--U..e.
e I I
cl
Stationarer
Beobachter
Gas Dynamics
Fig. Frequency Change by Moving the Disturbance Source
e f f
f =
"A'
=
I-Ule
=
I-Ma
In negative xcdirection it is computed:
f'
- f
=_f_
I+Ule
I+Ma
With
this
the Ma-number proves to be an
important
quantity
for
characterizing wave propagations in fluids.
When the case occurs that the velocity
of
the moving disturbance source
is equal to the propagation velocity
of
the disturbance, it results that the
propagation
of
the disturbances in relation to the disturbance source is possible
only in the half-plane from which the movement
of
the source takes place.
In the case that the velocity
of
the disturbance source exceeds the
propagation velocity
of
the disturbances, a propagation image develops which
is
shown in figure. The propagation
of
the disturbances in relation to the moving
disturbance source takes place within a cone, the socalled Mach cone. In front
of
the cone a disturbance-free area results which is strictly separated from the
Gas Dynamics
141
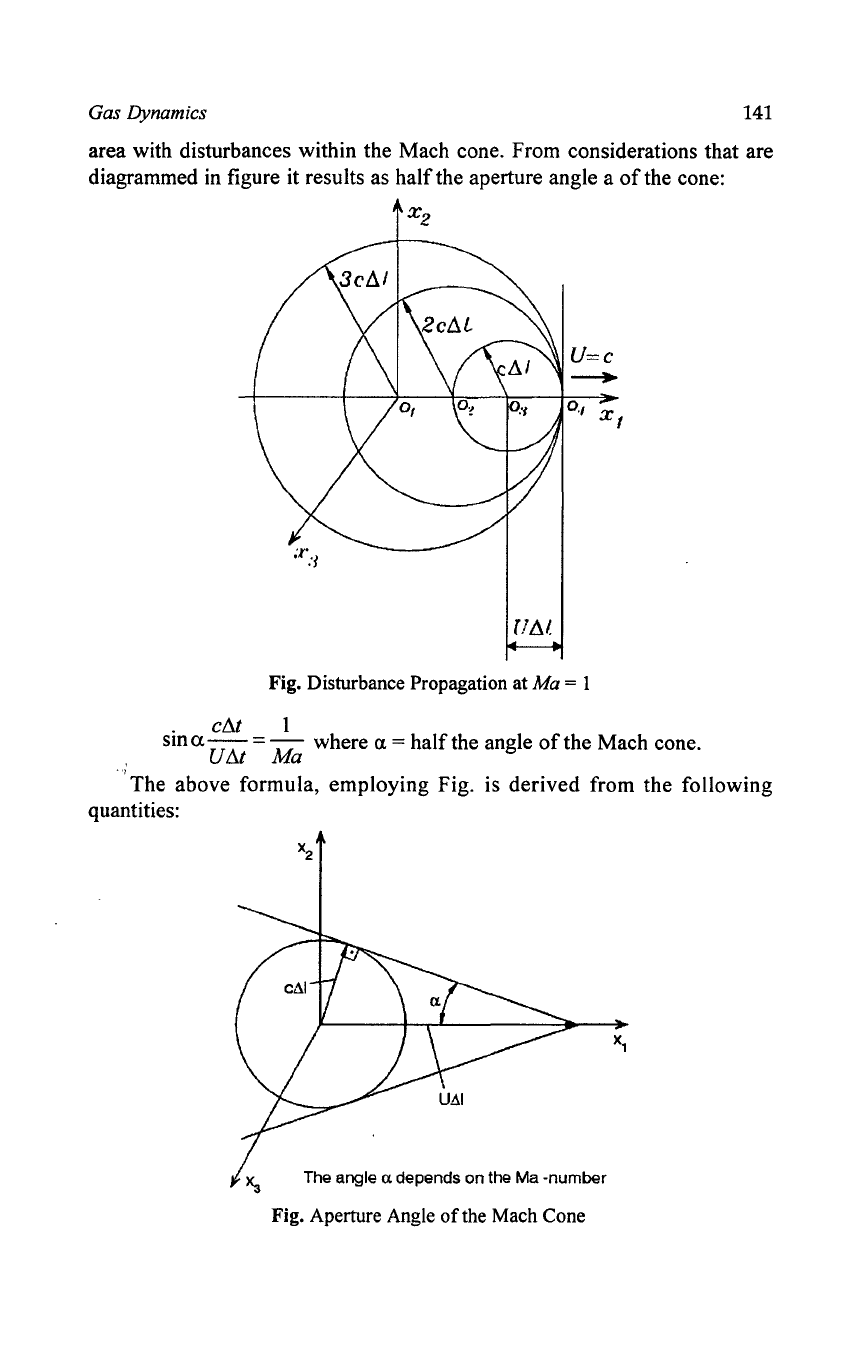
area with disturbances within the Mach cone. From considerations that are
diagrammed in figure it results as half the aperture angle a
of
the cone:
X
2
•
FAl
Fig. Disturbance Propagation at Ma = 1
. ellt 1
SID
a U
tlt
= Ma where a = half the angle
of
the Mach cone.
'The
above formula, employing Fig. is derived from the following
quantities:
Xa
The angle a depends
on
the Ma -number
Fig. Aperture Angle
of
the Mach Cone
