Brewster H.D. Fluid Mechanics
Подождите немного. Документ загружается.


142
cI'J.t
= propagation
of
the disturbance in the time
!J.t
u!J.t
= path
of
the disturbance source in the time
I'J.t
Gas Dynamics
When considerations are carried out
in
the two-dimensional sphere, the
Mach cone represents two lines crossing one another which are defined as
Mach lines or Mach waves The considerations stated above for spatial motions
can easily
be
employed for two-dimensional problems also. They show that
propagations
of
two-dimensional disturbances occur
in
the form
of
plane waves.
The propagation takes place vertically to the wave planes. •
With the aid
of
the above considerations observations can be explained
that
Region with
noise perception
Fig: Explanation for Perception
of
Aeroplanes
can be made
in
relation to the flight
of
supersonic aeroplanes. Aeroplanes
of
this kind show a region in which the aeroplane cannot be heard, i.e. an observer
can perceive an aeroplane flying towards him at supersonic speed much earlier
with the eye than he can hear
it. Only when the observer is within the Mach
cone, he succeeds in seeing and hearing the aeroplane.
NON-LINEAR
WAVE PROPAGATION,
FORMATION
OF
SHOCK WAVES
There it was explained that small disturbances
of
the fluid properties
p',
P', T' or
of
the flow velocity u', can be treated via linearizations
of
the
basic equations
of
flow mechanics.
On these assumptions a constant wave velocity resulted and a propagation
where a given wave form does not change was obtained. These properties are
not given any more for wave motions
of
larger amplitudes, so that wave
velocities form that change from place to place and wave-fronts develop that
deform with propagation. In order to understand such processes it
is
best to
consider the one-dimensional form
ofthe
continuity and momentum equation
with
U = U
I
'
X = x
I:
Continuity equation:
ap ap
au
-+-+p-
=0
at
ax
ax

Gas Dynamics
143
Momentum equation:
1
ap
pax
The following relation results for p = p(U):
dp
au
+ u
dp
au
+ p
au
= 0
dU
at
dU
ax
ax
Analogously, equation can
be
written:
au+uaU+~(dPJ(dP)aU
=0
at at
p
dp
dU
ax
.' When multiplying equation by
(dpldU)
and subtracting it from one
obtains:
p
au
=
~(dPJ(
d
P
)2
au
ax
p
dp
dU
ax
or transcribed:
~~
d~
l~~)
=±~
J(~~L
This equation can now be integrated:
1
dU
= ± J
J(:)
d:
p",
In consideration
of
P
Ipk
= const can be integrated::
p
k-\
d 2 [I
JP
U=
±
f.Jk.const.p
2
-.e.=±
__
vkpk-Iconst
p k
-1
p",
p",
2
U=
±--(a-c)
(k-l)
Thus for the propagation velocity
of
a wave
of
large amplitude:
a
z:::c±(k-l)U
2
results a propagation velocity
'"
a''', which depends on the local flow velocity.
Here c
is
the computed sound velocity for the undisturbed fluid.
When inserting equation one obtains the following relation:
144
Gas Dynamics
or transcribed:
au au
-+(U±a)-
=0
at
ax
From the continuity equation one obtains:
ap
+
(U
± a)
ap
= 0
at
ax
so that for p the following general solution
of
the differential equation can be
stated:
p =
Fp
(xl -
(U
l
±
a»
=
Fp
(Xl
-
(c
±
k;
1 U
I
})
where
Fp
0
is
a random function. Analogously it holds for the velocity:
U
I
=Fu
(xl -
(U
I
±
a»
=
Fu(XI-(C±
k;l
U
I
})
ct"
x
ttl
------
14+1
ct
x
+T
Ut
"
t
~--~~~------~~----------~-+-----
x
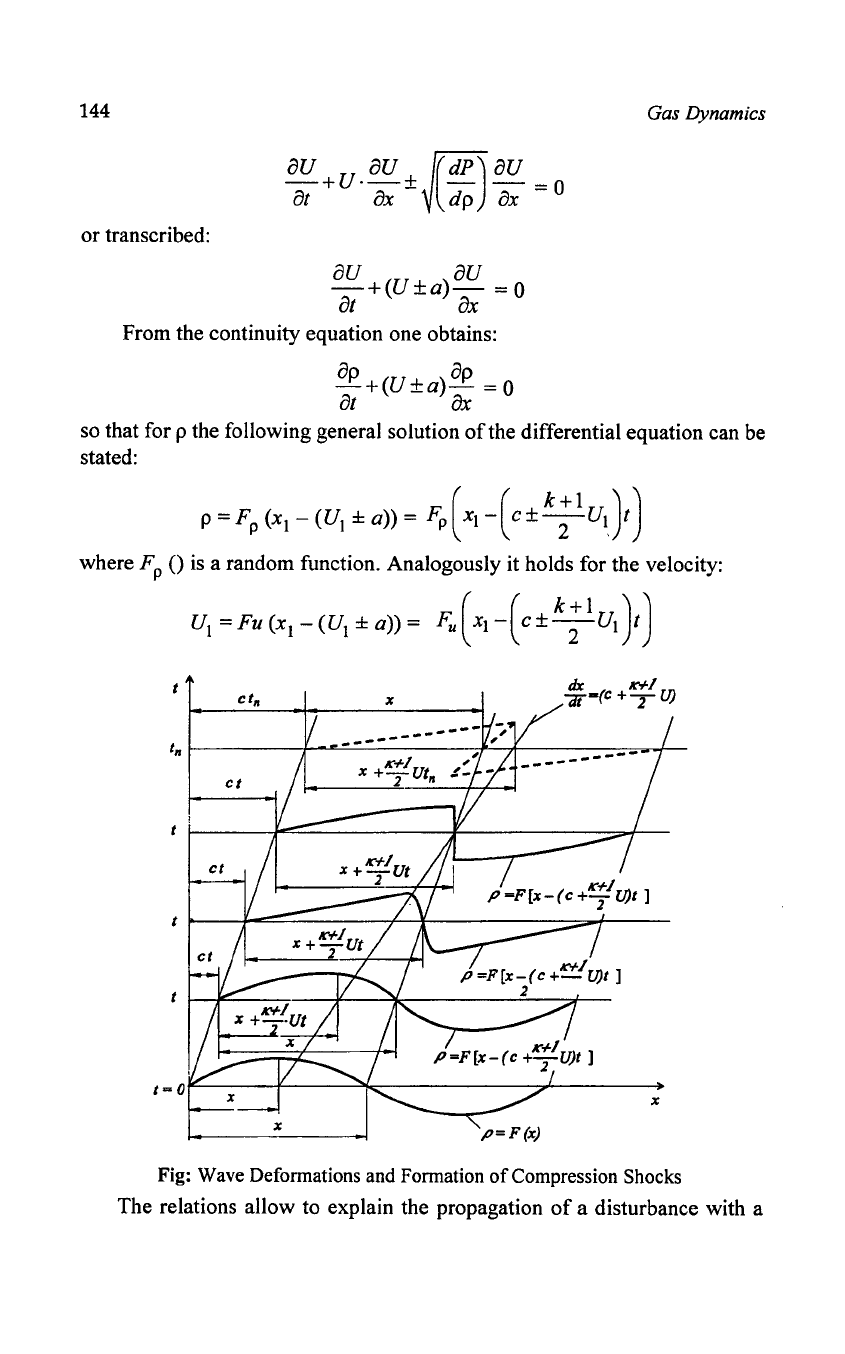
Fig: Wave Defonnations and Fonnation
of
Compression Shocks
The relations allow to explain the propagation
of
a disturbance with a

Gas Dynamics
145
k+l
propagation velocity
of
c ±
-2-
U
1
Because
of
this propagation velocity which
depends on the local flow velocity, wave deformations develop as they are
indicated. When
consirlering the propagating part with the (+) -sign, then
characteristic position changes
in
times t can be stated as follows:
,
k+lTT
xA=c·t(j);
XB=XA+cta+-2-uta;
XC=XB+ct
b
·
The developing and progressive deformation
of
the wave
is
apparent. Thus
the formation
of
compression forms comes about.
The local ambiguity
of
the density stated for
In
can
of
course not occur.
When the wave front has built up
in
a way that all thermo-dynamic quantities
of
the fluid and also the velocity experience sudden changes, the maximum
deformation possible
of
the propagating flow
is
reached. A compression shock
has built up.
ALTERNATIVE FORMS
OF
THE BERNOULLI
EQUATION
AQ
introduction
of
the stream tube theory into the treatment
of
fluid flows
one-dimensional isentropic flows were dealt with, employing the Bernoulli
equation for incompressible flows:
.!ul+-
k
-
P
=
_k_PH
2
(k-l)p
(k-l)pH
As thermo-dynamically possible maximum velocity it was determined,
for
(Pip)
~
0:
so that it holds:
1 2
12k
P
-VI
=
-U
max
----
2 2
(k
-I)
P
As the Ma-number represents a fundamental quantity
in
the treatment
of
gas-dynamic flow problems, it can be written:
1 =
(U
max
)2
_~
R~
=
(U
max
)2
__
2
__
1_
U
1
(k
-1)
Ut
U
1
(k
-1)
Ma
2
or transcribed:
_1
=
~[(Umax)2
-1]
Ma 2 U
1

1-1:6
Gas Dynamics
··-----------------------i r-------------------------
• •
l.
____
-=!
-
• •
PH,T H'P
H
:
....::.
U
L
r--
: T
q =
0:
i
PH'
H,P
H
· ,
______
•
__________________
J
•••
_
••
_________
••••••
___
•••
X
1
= 0 X
1
= L
Fig:
Compens~tion
Flow between two Pressure Tanks
At
the base
of
the above considerations was an expansion flow
as
it
is
indicated.
For
this flow results the so-called critical state, when U
I
= C
= U
c
is
reached,
i.e.
when the following relation holds:
2 2
~U2+~=~
2 c
(k
-I)
(k
-I)
For
the critical pressure it can be computed according to equation,
in consideration
of
equation:
[
k-lj
2k
Pc
T
2k
U
2
=
--RTH
1-(-)
=--RT
H
c
(k+l)
P
(k+l)
2k
~
=
;:
=Lk!l)J~-I)
Employing the relations for isentropic density
and
temperature
changes, one obtains:
(::)-:;
=
(~Jk
=[(k~l)f1j
(
T)
T*
=
(PPH*)kkl
= 2
T;
=T
H
(k+l)
The Mach number can now be employed to express the pressure,
temperature
and
density changes,
that
are possible
as
a result
of
the
Bernoulli equation for compressible media,
as
a function
of
the Mach
number:
2 2 T
1 2 C
CH
k
-I
2 H
-UI
+--
=
--
........
--Ma
+1=-
2
(k-I) (k-I)
2 T
or
transcribed:
Gas Dynamics
147
(~
J =
[1
+
(k
~
1)
Ma
2
r
1
For
the density
and
pressure variations the following relations can
be
derived:
F
or
the sound velocity relation c/e H it results:
c:
=(~
i =
[1+
k~1
Ma'
r
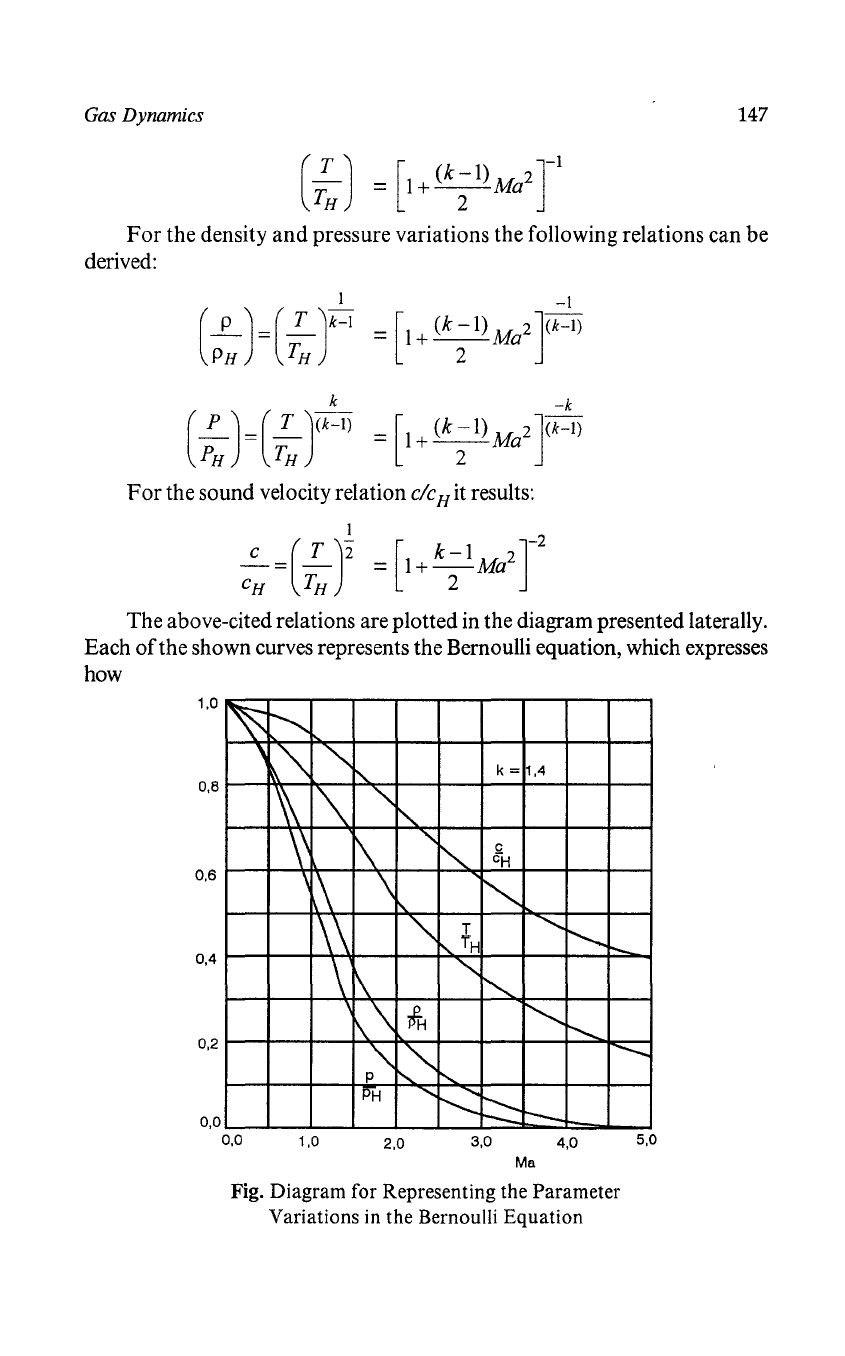
The above-cited relations are plotted in the diagram presented laterally.
Each
of
the shown curves represents the Bernoulli equation, which expresses
how
1,0
~
~
0,8
'~""
"
"-
k=
1,4
~
'\
"-
"-
\\
\
"-
"'"
g
cH
l\
\
'"
0,6
\\
"-
T
...........
f'...-
,
TH
r-
\
1\
"-
'"
0,4
'r--...\
~
I'--..
i'-...
0,2
P""-
,"-
--
0,0
0,0
1,0
PH
........
2,0
,
~
:::::
::--
3,0
4,0
Ma
Fig. Diagram for Representing the Parameter
Variations in the Bernoulli Equation
5,0

148
Gas Dynamics
he sound velocity, the temperature, the pressure
and
the density,
each
standardized with the corresponding values, change in the high-pressure tank
when the Mach-number changes are known. The temperature, density and
pressure
variations
(U/U
max
)
were
employed
as
a
parameter
of
the
representation.
It
is
a characteristic
of
compressible flows that the local stagnation pressure
ofa
flow
-pU
I
=
-pc
Ma
-p
- Ma
=-kPMa
1 2 1 2 2 1
(kP)
2 1 2
2 2 2 p 2
depends on the locally existing pressure and the local Mach number. For the
standardized pressure difference it holds:
PH-P
1 2 _ 2
PH
- P
__
2
_[
PH
-1]
"2PU1
- kMa
2
P - kMa
2
P
with
(PHIP)
from equation we obtain:
PH
-P
=
_2_[(1+
k-l
Ma2)(k~l)
-1]
!pU2
kMa
2
2
2
1 2
Via
a series expansion for
Ma
2
<
(k
-1)
it results:
PH
-P
1 1
If
2
2-k
If
4
(2-k)(3-2k)
If
6
-;:'-!---
=
+-lV.La
+--lV.La
+
lV.La
+ ...
1 U
2
4 24 192
-p
1
2
For incompressible flows it holds
Ma
= 0, so that
of
the series expansion
only 1 remains. The deviation
of
the developing pressure differences from the
stagnation pressure in compressible flows
is
therefore a function
of
the Mach
1
number. For
Ma
<
"3
the influence
of
the compressibility
on
the pressure
distribution is thus smaller
than one per cent.
FLOW
WITH
HEAT TRANSFER (PIPE FLOW)
An introduction into a sub-domain
of
flow mechanics and in particular
aims at deepening the physical comprehension
of
the fluid flows. For this
purpose often simplifications were introduced in the analytical problem
considerations. Adiabatic, reversible (dissipation-free) and one-dimensional
fluid flows were treated, i.e. isentropic flow processes
of
compressible media
which only depend on one space coordinate.
These considerations need some supplementary explanation in order to

Gas Dynamics
149
be able to understand special phenomena in the case
of
flowswith heat transfer.
For dealing with such flows which can be considered as stationary and one-
dimensional, i.e. experience changes only
in
the flow direction
xl
= X the
following basic equations are at disposal which are stated by
U
I
= U
• Mass conservation:
pFU
= in = const
• Momentum equation:
pu
dU
_ _
dP
dx
dx
• Energy equation:
(dq) =
CvdT+Pd(~)
=
CpdT-~dP
• State equation for ideal gases:
P
-
=RT
P
From the mass-conservation equation one obtains:
dp
dU
dF
-+-+-
=0
P U F
dF
or
for pipe flows with F =
0:
dU
dp
-
=--
U P
From the ideal gas equation it can be derived:
dP
dp
dT
=-+-
P p T
and from the momentum equation one obtains -
dp
= U
dU
or
p
dP P 1 2
dU
=-UIdUI=-U
-
P P
RT
U
With kRT =
c2
and from the momentum equation one obtains:
_ dP _
~U2
dU
= KMa
2
dU
P - c
2
U U
When finally including the energy equation into the considerations, it
can be stated:
dP
(dq) = C pdT - - = C pdT + UdU
P

150
Gas Dynamics
or
transcribed:
dU
= (dq) _
cpdT
=_I_(~)(dq)
=_I_~dT
U U
2
U
2
Ma
2
KRT C
Ma
2
KRT
p
i.e. it holds for the relative velocity change in a pipe flow as a result
of
heat supply:
dU
1
((d
q
)
dT)
ij=
(K-l)Ma
2
-h--T
where h = cpT was set. From equation it follows:
dT
= dP _
dp
=-KMa
2
dU
+
dU
T P P U U
or transcribed:
dT
=
(1-
KMa2)
dU
T U
This relation inserted in equation yields:
dU
= 1
((d
q
)
_(I_KMa
2
)dU)
U
(K-l)Ma
2
h U
,
dU
Solved in terms
of
ij
one obtains:
dU
1 (dq)
-=----:--
U
(l-Ma
2
)
h
This relation inserted in ) yields for the relative density change:
dp
-1
(dq)
-;=
(1-Ma
2
)
h
or for the relative changes in pressure and temperature it holds:
dP -KMa
2
(dq)
dT
(1-
KMa
2
)
(dq)
= and -
~----,,--'-
P
(l-Ma
2
)
h
T-
(1-Ma
2
)
h
For the local change
of
the Ma number it can also be derived:
d(Ma
2
) =
d(U
2
/c
2
)
=~d(U2)=2dU
_
dT
Ma
2
(U
2
/c
2
) U
2
T U T
Thus for the change
of
the Ma-number with heat supply it holds:
dMa
2
(1
+
KMa
2
)(dq)
--
=
----,:--
Ma
2
(1-Ma
2
)
h
As (dq) =
T·
ds and h = c
p
.
T it holds furthermore:
dMa
2
(l
+
KMa
2
)
ds
Ma
2
=
(l-Ma
2
) c
p

Gas Dynamics
151
The
above relations can now be employed for understanding
how
P,
T,
p, U and Ma change locally when one conveys heat to a pipe flow; i.e. dqlh>
0:
Subsonic Flow:
dU
> 0 ; the flow velocity increases with heat supply
U
dp
> 0 and dP <
0;
density and pressure decrease with heat supply.
p P
dT
fl
T >
0;
the temperature increases with heat supply for Ma <
'\j~.
n .
fl
T <
0;
the temperature decreases in spite
of
heat supply for
Ma
>
'\j~.
dMa
2
--2-
> 0;
the
local Ma-number increases with heat supply
Ma
The above relations indicate that in spite
of
heat supply there is a decrease
in temperature for
.J1I
K <
1.
Supersonic Flow:
dU
U
I
I
<
0;
the flow velocity decreases with heat supply.
d:
> Oand
~
>
0;
density and pressure increase with heat supply.
dT
T>
0;
the temperature increases with heat.supply.
dMa
2
--2-
<
0;
the local Ma-number decreases with heat transfer.
rna
The change
of
fluid-mechanical and thermo-dynamical state quantities
in a pipe flow in principle takes place in a different way in the supersonic
range than in the subsonic region.
When
for deepening
the
physical comprehension one
considers
the
occurring processes in the T -s-diagram for an ideal gas, one obtains:
(dq)v = C
v
·dT
v
=T·ds
v
~(aT)
=~
as v C
v
d)
= cpdTp =
Tds
p
~(aT)
=I-
( q p
as
p cp
From equation one obtains for the temperature change
in
a pipe flow with
heat supply:
