Бронов С.А. Методы оптимизации в САПР

Подождите немного. Документ загружается.

101

этом всё равно не удаётся обойти промежуточные неоптимальные варианты,

но число рассмотренных вариантов занимает малую долю их общего числа,

что существенно уменьшает объём вычислений. Симплекс-метод предлагает

такую процедуру вычислений. Его достоинством является использование

матричного представления задачи, что позволяет легко его алгоритмизиро-

вать и применять как в универсальных математических программах (напри-

мер, MathCAD), так и в электронных таблицах (например, Excel).

Постановка задачи для симплекс-метода всегда выполняется в канони-

ческой форме, к которой следует привести исходную форму задачи, хотя со-

временные программные средства часто сами умеют выполнять необходи-

мые предварительные преобразования ввиду их простоты. При этом появля-

ется набор переменных, включающий



переменных (

исходных пере-

менных и

дополнительных). Эти переменные при большинстве вычисле-

ний в рамках симплекс-метода равноправны. Если число переменных равно

числу уравнений, то полученная система линейных уравнений имеет одно

решение, которое и является оптимальным. Но, как правило, общее число пе-

ременных оказывается больше числа уравнений. Это означает, что часть пе-

ременных — избыточна. Им можно придать любые значения (например, ну-

левые), а остальные — рассчитать. Поэтому вся совокупность



пере-

менных разделяется на переменные, которые не участвуют в расчётах

(например, обнуляются) и называются небазисными, и те, которые участвуют

в расчётах и называются базисными. Рассчитываемые переменные могут

принимать в процессе расчётов различные значения. Если они оказываются

отрицательными, то полученные решения называются недопустимыми, а ес-

ли неотрицательными — то решения называются допустимыми.

Принцип работы симплекс-метода можно проиллюстрировать на приме-

ре следующей задачи. Пусть задана задача линейного в следующем виде:

целевая функция: max45)(







xxxI ,

ограничения:



















.0,

;2)(

;1)(

;62)(

;2446)(

213

212

211

xxq

xxxq

Она может быть представлена в канонической форме:

целевая функция: max000045)(

432121







ssssxxxI ,

102

ограничения:



















,0,,,,,

;2)(

;1)(

;62)(

;2446)(

432121

424

3213

2212

1211

ssssxx

sxxq

sxxxq

где первые четыре уравнения были получены из ограничений типа "меньше

или равно" (так как дополнительные переменные

введены со знаком плюс),

а совокупность ограничений в последней строке определяет все переменные

как неотрицательные.

В условиях задачи для наглядности основные переменные обозначены

буквой

, а вводимые при переходе к канонической форме дополнительные

переменные — буквой

, но и те, и другие в процессе решения равноправны.

Различия между ними проявляются в том, что основные переменные участ-

вуют в расчёте целевой функции (т. е. в проверке критерия оптимальности), а

дополнительные — нет, так как входят в целевую функцию с коэффициента-

ми 0.

Рассматриваемая задача — двумерная и поэтому имеет геометрическое

решение, которое в данном случае будет использоваться как иллюстрация

работы симплекс-метода.

2 3 4 5

Область

допустимых

решений

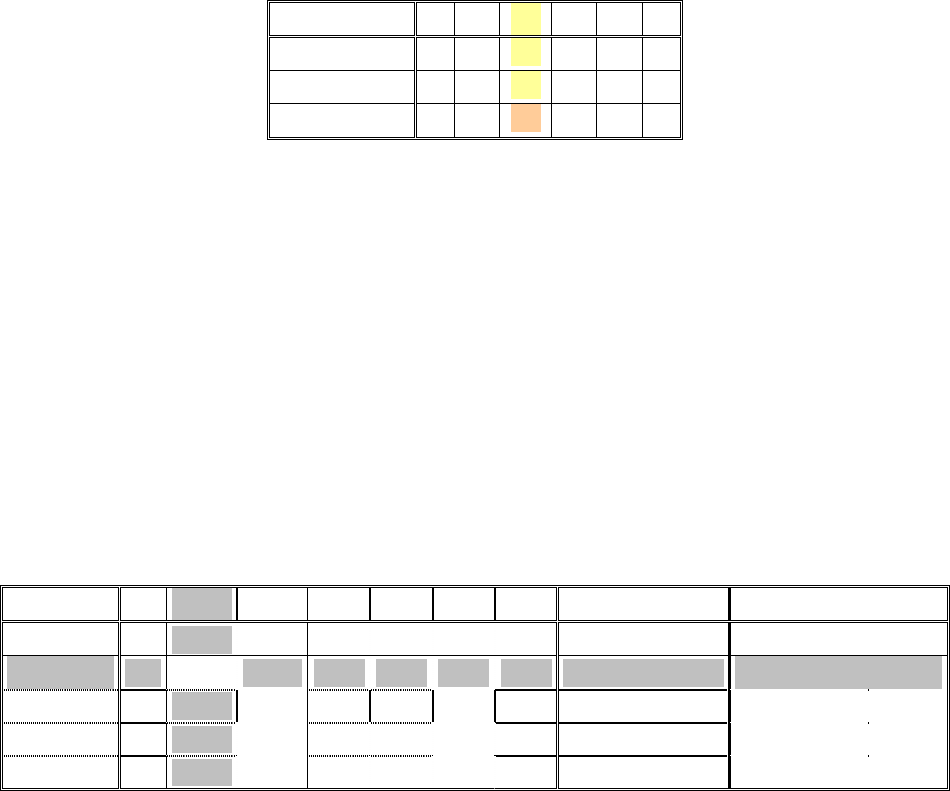
Рисунок 5.4 — Геометрическое представление задачи

для иллюстрации симплекс-метода

103

Геометрическое представление задачи (Рисунок 5.4) содержит в коорди-

натах

, xx линии ограничений

q ,

q , ограничивающие область до-

пустимых решений

ABCDEF

. Как и положено в задачах ЛП, эта область —

выпуклая и решение находится в одной из точек:

или

. Ес-

ли воспользоваться графическим методом и нанести на график линию целе-

вой функции, то можно, перемещая её параллельно самой себе, найти точку

оптимума (в данном случае — максимума).

На графике видны координаты точек, которые можно свести в таблицу:

B C D

E F

0 4 3 2 1 0

0 0 1,5

2 2 1

I=5 x

+4 x

0 20

21 18

Судя по таблице, максимум целевой функции достигается в точке

. Но

в случае аналитического решения задачи, оптимальность точки

не являет-

ся явной, её ещё необходимо найти.

Для использования симплекс-метода следует целевую функцию перепи-

сать в виде равенства:

045





xxI ,

а всю задачу линейного программировать представить в виде таблицы

(Таблица 5.2).

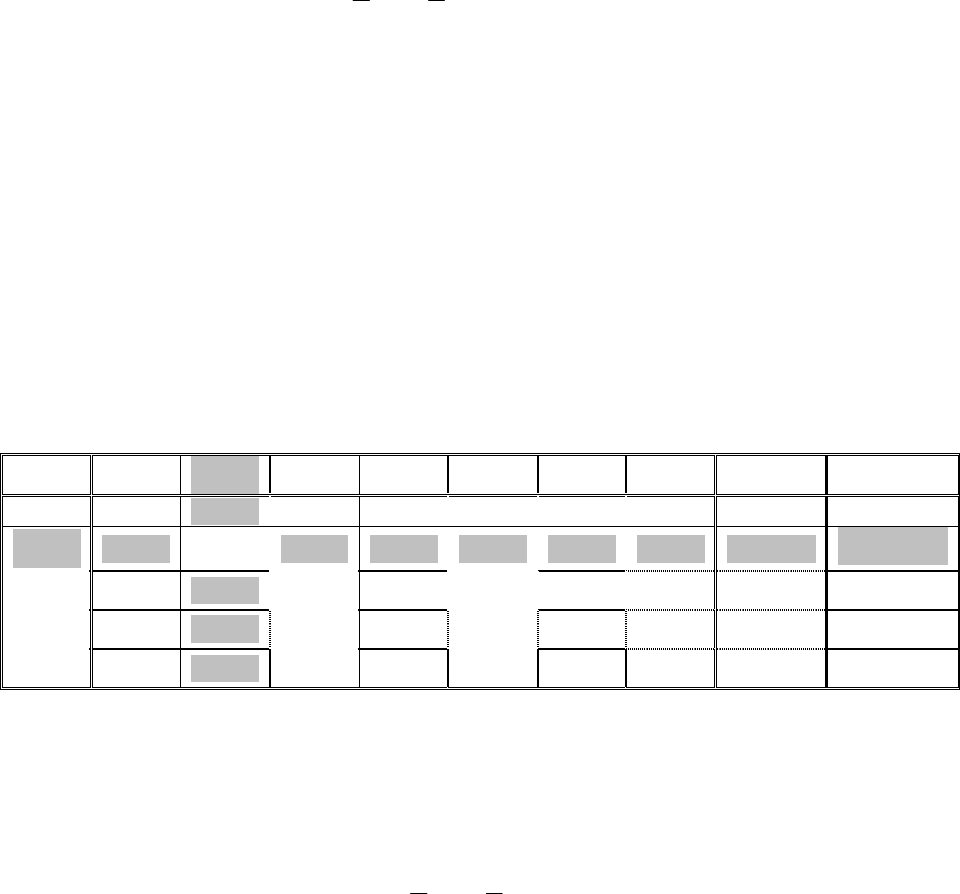
Таблица 5.2 — Задача линейного программирования для симплекс-метода

(шаг 1)

Базис

I x

Решение Пояснение

1 –5 –4 0 0 0 0 0

I -строка

0 6 4 1 0 0 0 24

-строка

0 1 2 0 1 0 0 6

-строка

0 –1 1 0 0 1 0 1

-строка

0 0 1 0 0 0 1 2

-строка

Таблица 5.2 сформирована следующим образом. В колонке Базис ука-

зываются те переменные, которые будут использоваться для определения

решений (базисные переменные). В данном случае базисными являются все

дополнительные переменные

, а небазисными являются все основные пере-

менные

. Это связано с тем, что в симплекс-методе в качестве начальной

точки обычно берётся начало координат, в котором все

равны нулю. В

первой строке перечислены все переменные, входящие в задачу:

из целе-

вой функции, два

и четыре

. В соответствующих колонках приводятся

104

значения этих переменных на начальном шаге — они просто переписаны из

системы уравнений. В частности, в колонке

присутствует 1 только в пер-

вой строке, относящейся к целевой функции, что соответствует записанному

на её основе уравнению; в остальных строках (соответствующих ограничени-

ям)

отсутствует, поэтому записаны 0.

В колонке Решение приводятся правые части соответствующих уравне-

ний на начальном шаге. В колонке Пояснение записаны подсказки для

наглядности:

-строка — строка для целевой функции (она всегда будет

оставаться),

-строки на начальном шаге относятся к соответствующим

ограничениям. В последующем эти строки будут меняться.

Итак, на начальном шаге в качестве базиса выбираются

и все допол-

нительные переменные

(первая колонка), а основные переменные

обну-

ляются. Эта система уравнений даёт решение, которое будет соответствовать

некоей начальной точке. Формально решение системы четырёх линейных

уравнений для четырёх неизвестных имеет вид:

1000

0100

0010

0001



Ввиду того, что матрица слева является единичной, решение находится

просто и без вычислений: 0



x , 0



x , 24



s , 6



s , 1



s , 2



s , где

учтено, что основные переменные

были приняты равными нулю.

Здесь характерно следующее. Обнуление основных переменных

на

начальном шаге и использование в качестве базисных только дополнитель-

ных переменных

является универсальным приёмом, который всегда воз-

можен, если все ограничения исходной задачи были неравенствами. Именно

в этом случае число дополнительных переменных равно числу ограничений и

соответствующая матрица становится единичной.

Является ли найденное решение оптимальным? Для оценки оптимально-

сти следует вычислить целевую функцию в найденной точке 0



x , 0



x ,



s , 6



s , 1



s , 2



s : 0000045)(

432121







ssssxxxI . Оче-

видно, что начальное решение не будет оптимальным, так как любое увели-

чение любого

приведёт к возрастанию значения целевой функции, т. е. это

новое значение будет больше исходного нулевого и ближе к оптимальному.

Поэтому необходимо сделать следующий шаг: следует заменить систему

уравнений, приравняв одну из дополнительных переменных

нулю и введя

105

вместо неё одну из основных переменных

. Таким образом будет осуществ-

лён переход к новой угловой точке.

Какую основную переменную вместо какой дополнительной перемен-

ной следует ввести?

В качестве вводимой следует выбрать ту основную переменную, которая

находится при наибольшем положительном коэффициенте в целевой функ-

ции (т. е. при наибольшем отрицательном коэффициенте в

-строке табли-

цы), потому что при этом движение к максимуму целевой функции будет бо-

лее быстрым, эта переменная —

x .

Выбор исключаемой переменной среди

более сложен: нужно выбрать

и исключить наименее перспективную переменную. Каждая переменная

соответствует своему ограничению. Поскольку вводится новая переменная,

то следует соотнести исключаемую переменную с вводимой. В данном слу-

чае вводимой переменной является

x . Точки её пересечения с ограничения-

ми имеют следующий физический смысл: эта переменная не может быть

больше своего значения в точке пересечения. Поскольку исходная система

ограничений-неравенств "меньше или равно", то самым сильным ограниче-

нием будет наименьшее, которое и следует выбрать.

Итак, необходимо решить четыре неравенства (из ограничений):

















,20

;62

;2446

находя точки пересечения их с осью

x , т. е. при 0



x .

Тогда получается серия решений:



















,20:

;1;1:

;6;6:

;246:

114

113

112

111

xxq

что можно представить на оси

x следующим образом:

106

-1

∞

Рисунок 5.5 — Выбор исключаемой переменной на 2-м шаге

Для выбора исключаемой переменной следует проанализировать полу-

ченные результаты. Условие с переменной

s не представляет интереса, так

как не накладывает реальных ограничений, поскольку означает лишь то, что

переменная

x должна быть неотрицательной. Условие

q также не пред-

ставляет интереса, так как указывает, что переменная

x не должна быть бес-

конечно большой. Интерес представляют конкретные положительные значе-

ния

x , связанные с ограничениями

q (соответствует переменной

s ) и

(соответствует переменной

s ). При этом ограничению с

s соответствует

меньшее значение 4



x . Поэтому именно переменную

s следует исклю-

чить из базиса. Формально алгоритм нахождения исключаемой переменной

следующий: используя ограничения, следует вычислить значения вводимой

переменной, а затем для исключения выбрать ту дополнительную перемен-

ную, которой соответствует наименьшее положительное значение исключае-

мой переменной, полученной в ходе указанного решения.

В результате появляется новая система уравнений, представляемая в ви-

де следующей таблицы (Таблица 5.3).

Для её формирования используется следующий алгоритм:

1) выбирается ведущий элемент на пересечений ведущего столбца (в

данном случае для вводимой переменной

x ) и ведущей строки (в данном

случае для исключаемой переменной

s );

2) прежняя ведущая строка (в данном случае для

s ) исключается, а вме-

сто неё вводится новая ведущая строка

x ;

3) вычисляются элементы новой ведущей строки:

элементведущий

строкаведущаяпрежняя

строкаведущаяновая  , в данном случае:

2446

121121

121







sxxsxx

sxx

;

4) вычисляются элементы каждой последующей строки:

107

строкаведущаяэлементепервомприткоэффициен

строка

прежняя

строка

новая







)(

в данном случае:

-строка:





 























4000

0000045

432121

ssssxx

 

   

)200(0000

4)55(

2121

































ssxx

20000

432121

 ssssxx ;

q -строка:





 





















4000

6001021

432121

ssssxx

 

   

)46(0000

2)11(

2121

































ssxx

2001

432121

 ssssxx ;

q -строка:





 























4000

1010011

432121

ssssxx

 

   

)41(0001

1)11(

2121

































ssxx

5010

432121

 ssssxx ;

q -строка:

108





 





















4000

2100010

432121

ssssxx













   

)02(0100

000001)00(

2121















ssxx

2100010

432121





ssssxx .

Таким образом, сформирована Таблица 5.3. В ней небазисные перемен-

ные

x и

s равны нулю (они отсутствуют в столбце Базис). В столбце Реше-

ние представлено новое базисное решение: 4



x , 2



s , 5



s , 2



s и

новое значение целевой функции



Таблица 5.3 — Задача линейного программирования для симплекс-метода

(шаг 2)

Базис

Решение Пояснение

1 0 -2/3 5/6 0 0 0 20

-строка

0 1 2/3 1/6 0 0 0 4

x -строка

0 0 4/3 -1/6 1 0 0 2

q -строка

0 0 5/3 1/6 0 1 0 5

q -строка

0 0 1 0 0 0 1 2

q -строка

Является ли полученное базисное решение оптимальным? Для ответа на

этот вопрос необходимо снова проанализировать коэффициенты в

-строке,

т. е. в целевой функции, которая может быть представлена в виде уравнения:

 sxI ,

из которого видно, что при увеличении переменной

x может произойти

увеличение значения целевой функции. Поскольку в данный момент 0



(они отсутствуют в базисном столбце таблицы), то такое увеличение вполне

возможно. Следовательно, следует сделать ещё один шаг, перейти к новой

угловой точке и получить новую симплекс-таблицу.

Дальнейшие действия аналогичны описанным выше на шаге 2.

В качестве вводимой вновь следует выбрать ту основную переменную,

которая находится при наибольшем положительном коэффициенте в целевой

функции (т. е. при наибольшем отрицательном коэффициенте в

-строке

таблицы), потому что при этом движение к максимуму целевой функции бу-

109

дет более быстрым, эта переменная —

x (Таблица 5.3). При переменной

x — коэффициент равен нулю, что является следствием выполненного ранее

шага.

Далее необходимо выбрать новую исключаемую базисную переменную

(из столбца Базис) и новую вводимую переменную из строки Базис (Таблица

5.3). Теоретически кандидатами на исключения могут быть переменные

s или

s . Исключать

x не понадобится, так как, во-первых, она была толь-

ко что введена на предыдущем шаге, а во-вторых, коэффициент перед

x в

целевой функции (Таблица 5.3) равен нулю, т. е. она не влияет на значение

целевой функции в полученной симплекс-таблице.

Как было сделано выше, нужно выбрать и исключить наименее пер-

спективную переменную. Каждая переменная

соответствует своему огра-

ничению. Поскольку вводится новая переменная, то следует соотнести ис-

ключаемую переменную с вводимой. В данном случае вводимой переменной

является

x . Точки её пересечения с ограничениями имеют следующий фи-

зический смысл: эта переменная не может быть больше своего значения в

точке пересечения. Поскольку исходная система ограничений-неравенств

"меньше или равно", то самым сильным ограничением будет наименьшее,

которое и следует выбрать.

Итак, необходимо решить четыре неравенства (из ограничений):













,2,2:

;3;5

;

;6;4

224

223

222

221

xxq

xxx

находя точки пересечения их с осью

x , т. е. при 0



x , из которых получена

серия решений, что можно представить на оси

x следующим образом:

3/2

Рисунок 5.6 — Выбор исключаемой переменной на 3-м шаге

110

Наименьшему значению соответствует переменная

s (соответствующая

ограничению

q ), которая и становится исключаемой переменной.

Таким образом, ведущим столбцом становится столбец

x , а ведущей

строкой — строка

q . После вычислений, аналогичных приведённым выше,

получается новая симплекс-таблица (Таблица 5.4).

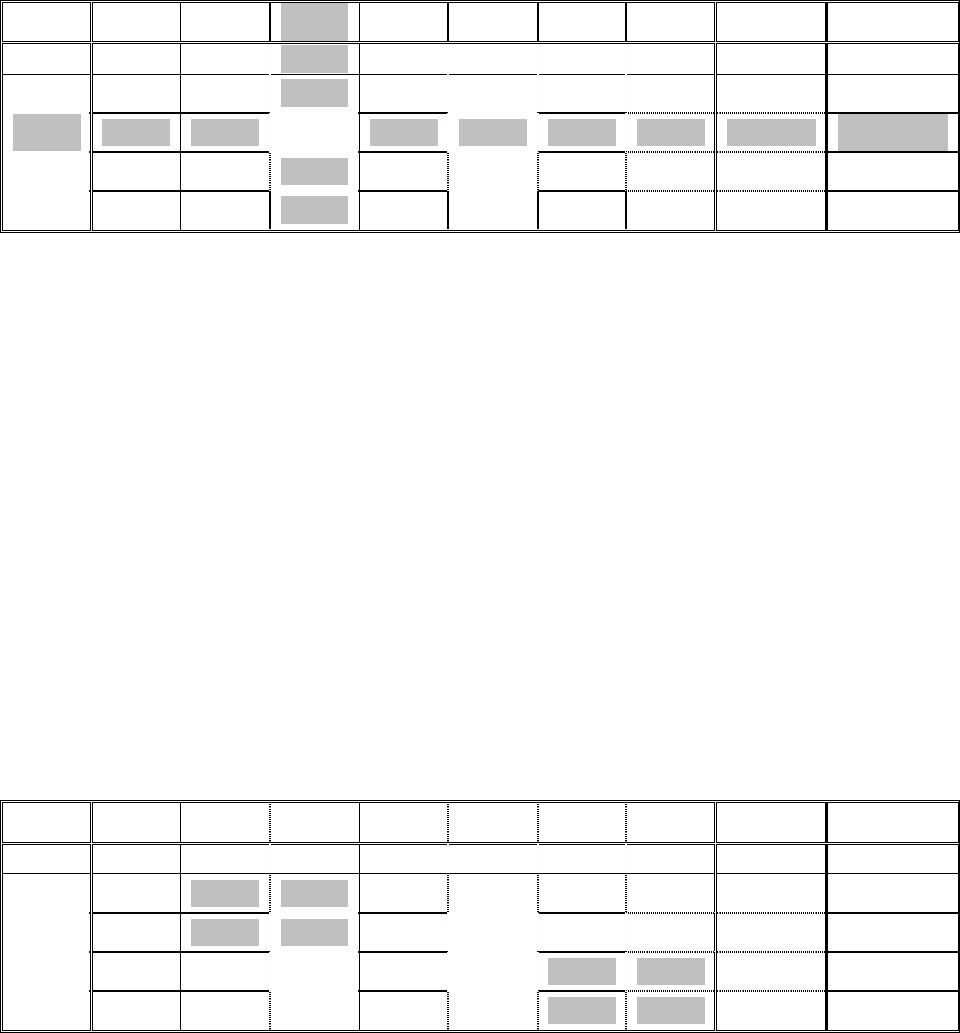
Таблица 5.4 — Задача линейного программирования для симплекс-метода

(шаг 3)

Базис

Решение Пояснение

1 0 0 3/4 1/2 0 0 21

-строка

0 1 0 1/4 -1/2 0 0 3

x -строка

0 0 1 -1/8 3/4 0 0 3/2

x -строка

0 0 0 3/8 -5/4 1 0 5/2

q -строка

0 0 0 1/8 -3/4 0 1 1/2

q -строка

В полученной симплекс-таблице (Таблица 5.4) в

-строке нет отрица-

тельных коэффициентов, а перед основными переменными

x и

x — нуле-

вые коэффициенты, что означает, что никакие изменения

x и

x не могут

более увеличить значение целевой функции, которое равно 21. Следователь-

но, это значение целевой функции — максимальное. Поскольку решается за-

дача максимизации, то она решена и полученное решение — оптимальное:



x , 2/3



x ,



. Значения дополнительных переменных не играют

роли, так как они являются вспомогательными переменными.

Вид результирующей симплекс-таблицы имеет характерные особенно-

сти (Таблица 5.5): подматрицы для основных переменных

x и

x , а также

вспомогательных

s и

s — единичные.

Таблица 5.5 — Характерный вид результирующей симплекс-таблицы

Базис

Решение Пояснение

1 0 0 3/4 1/2 0 0 21

-строка

0 1 0 1/4 -1/2 0 0 3

x -строка

0 0 1 -1/8 3/4 0 0 3/2

x -строка

0 0 0 3/8 -5/4 1 0 5/2

q -строка

0 0 0 1/8 -3/4 0 1 1/2

q -строка