Бронов С.А. Методы оптимизации в САПР
Подождите немного. Документ загружается.


81
случае наличия того и другого. Например (Рисунок 4.1), может существовать
два локальных максимума:
1max
x и
2max
x . Сравнение их между собой даёт
)()(
1max2max
xIxI
, т. е. глобальным максимумом является
2max
x . Аналогич-
но этому, можно выявить два локальных минимума:
1min
x и
2min
x , анализ ко-
торых даёт )()(
2min1min
xIxI
, т. е. глобальным минимумом является
1min
x .
Но у метода есть и существенные недостатки.
Во-первых, не всегда понятно, какими должны быть левая
a
x и правая
b
x границы интервала: в общем случае это, соответственно, –∞ и +∞. Если
решается задача условной оптимизации (т. е. имеются ограничения), то ино-
гда это помогает определиться с границами. Например, если наложено огра-
ничения, что все
0
x
, то левая граница совпадает со значением 0
a
x и от
неё можно двигаться вправо. Иногда существуют ограничения справа, и то-
гда интервал становится вполне конкретным. Поскольку в технических при-
ложениях изучаются реальные процессы, то реальные оптимизационные за-
дачи оказываются с ограничениями и тогда рассматриваемый метод вполне
применим.
Во-вторых, нет однозначных рекомендаций по выбору шага
. В ре-
зультате точка экстремума определяется с погрешностью, которую принято
определять равной половине шага
5
,
0
. Погрешность можно уменьшить,
увеличивая число шагов на интервале, но это сразу увеличивает время счёта,
что особенно заметно, если вектор
x
имеет большую размерность и нужно
осуществлять перебор одновременно по всем составляющим вектора
x
.
Метод равномерного поиска можно было бы считать идеальным мето-
дом, если бы не эти недостатки. Поэтому, когда существуют границы интер-
вала и есть возможность выбрать шаг с допустимой погрешностью, его ис-
пользуют как наиболее простой, так как модность современных ЭВМ позво-
ляет быстро осуществлять перебор большого числа значений, особенно, если
целевая функция не очень сложная.
Формально метод равномерного поиска представляется следующим об-
разом:
1) задаются левая
a
x и правая
b
x границы начального интервала и число
точек
N
;
2) определяются точки
1
)(
)1(
N
xx
kxx
ab
ak
,
N
k
,...,
1
, равностоя-
щие друг от друга;
3) в найденных точках вычисляются значения целевой функции )(
k
xI ;
82
4) осуществляется перебор массива всех значений целевой функции и
находятся максимальное )]([max
1
max k
Nk
xII
и минимальное
)]([min
1
min k
Nk
xII
значения;
5) определяется, каким интервалам принадлежат
k
x , соответствующие
максимуму и минимуму целевой функции;
6) определяется значение ],[
11min
kkk
xxxxx для минимума или
],[
11max
kkk
xxxxx для максимума.
Тип экстремума, как правило, задан заранее, но иногда в рамках одной
поисковой процедуры ищутся сразу оба типа экстремума — всё зависит от
физического смысла задачи.
83
5 Линейное программирование
5.1 Пример постановки оптимизационной задачи как задачи
линейного программирования
Линейное программирование (ЛП) — это определённый способ пред-
ставления и решения задач оптимизации, в которых целевая функция, а так-
же ограничения представляют собой линейные выражения от нескольких не-
зависимых переменных. Слово программирование не имеет отношения к
языкам программирования, а связано с понятием оптимальная программа
выпуска продукции или оптимальная программа деятельности и появилось
тогда, когда языков программирования ещё не было.
Ниже приводится пример ситуации, которая может быть представлена в
понятиях ЛП.
Пример 5.1. Некая фирма производит краску двух типов: К1 и К2. При
этом используются три типа исходного сырья: С1, С2 и С3. Известно, что для
производства 1 тонны краски К1 требуется: 1
1,1
a тонна сырья С1, 6
1,2
a
брикетов сырья С2 и 32
1,3
a литра сырья С3. Для производства одной тон-
ны краски К2 требуется: 2
2,1
a тонны сырья С1, 3
2,2
a брикета сырья С2
и 36
2,3
a литров сырья С3. Объём используемого сырья ограничен (напри-
мер, из-за ограниченных возможностей складских помещений): сырья С1
может использоваться не более 20 тонн ( 20
max1
C ), сырья С2 — не более
60 брикетов ( 60
max2
C ), сырья С3 — не более 400 л ( 400
max3
C ). При реа-
лизации цена 1 тонны краски К1 составляет 30000
1
b рублей, а краски К2
20000
2
b . Вся краска продаётся без ограничений.
Требуется определить, сколько какой краски следует произвести, чтобы
получить наибольшую прибыль.
Условия задачи можно записать в виде таблицы (Таблица 5.1).

84
Таблица 5.1 — Весовые коэффициенты задачи линейного программирования
для производства краски
№
Тип
функции
Обозначение
функции
Весовые коэффициенты
на 1 тонну красок
Предельная
величина
Краска К1:
1
x
Краска К2:
2
x
1
Целевая функция, руб.
)
(
x
I
20000
1
b
30000
2
b
max
2
Использование сырья С1,
тонны
)(
1
xq
1
1,1
a 2
2,1
a
20
max1
C
3
Использование сырья С2,
брикеты
)(
2
xq
6
1,2
a 3
2,2
a
60
max2
C
4
Использование сырья С3,
литры
)(
3
xq
32
1,3
a 36
2,3
a
400
max3
C
В таблице переменными
1
x и
2
x обозначены массы соответствующих
типов краски (в тоннах), которые необходимо найти в ходе решения задачи.
Задача формулируется всегда таким образом, чтобы все остальные парамет-
ры являлись весовыми коэффициентами, которые умножаются на эти пере-
менные. Интересно, что весовые коэффициенты могут иметь различную фи-
зическую природу и, соответственно, различные единицы измерения.
Например, коэффициенты в выражении
1
q измеряются в тоннах, в выраже-
нии
2
q — в брикетах, а в выражении
3
q — в литрах. Размерность перемен-
ных
1
x и
2
x также может быть разной, но произведение весового коэффици-
ента на переменную должно приводить к одной и той же физической вели-
чине в одних и тех же единицах измерения. Это связано с тем, что произве-
дения весовых коэффициентов на переменные суммируются, а суммировать
можно только однородные составляющие.
Общий доход при продаже обоих типов краски
212211
2000030000)( xxxbxbxI
, (5.1)
где
1
x ,
2
x (составляющие вектора
x
) — масса в тоннах соответственно пер-
вой (К1) и второй (К2) красок;
1
b ,
2
b — стоимость 1 тонны соответствующей
краски.
Поскольку общий доход должна быть максимальным, то выражение
(5.1) является целевой функцией, которую следует максимизировать, т. е.:
max2000030000)(
212211
xxxbxbxI . (5.2)
Из физической сути задачи вытекает, что
1
x ,
2
x должны быть неотрица-
тельными, т. е. больше или равны нулю (отрицательность
1
x и
2
x означала
бы, что краски не производятся, а потребляются):

85
0
1
x , 0
2
x . (5.3)
Если стремиться к максимизации функции (5.2) без каких-либо ограни-
чений, то это будет достигнуто при бесконечно больших значениях
1
x и
2
x .
Но в действительности в условии задачи имеются ограничения, связанные с
объёмами доступного сырья, которые приводят к следующим выражениям:
.4003632)(,)(
;6036)(,)(
;2021)(,)(
213max322,311,33
212max222,211,22
211max122,111,11
xxxqCxaxaxq
xxxqCxaxaxq
xxxqCxaxaxq
(5.4)
Смысл приведённых ограничений в том, что невозможно использовать
больше сырья, чем имеется в распоряжении производителя.
Выражения (5.2), (5.3) и (5.4) являются формулировкой задачи в виде за-
дачи линейного программирования.
Решать задачу (5.2) необходимо следующим образом. Поскольку имеет-
ся лишь две переменных
1
x и
2
x , то можно представить последовательность
решения графически в плоскости этих двух переменных.
Первоначально следует отобразить все линии ограничений. Для этого
неравенства (5.4) заменяются равенствами:
,4003632)(
;6036)(
;2021)(
213
212
211
xxxq
xxxq
xxxq
(5.5)
которые строятся на плоскости.
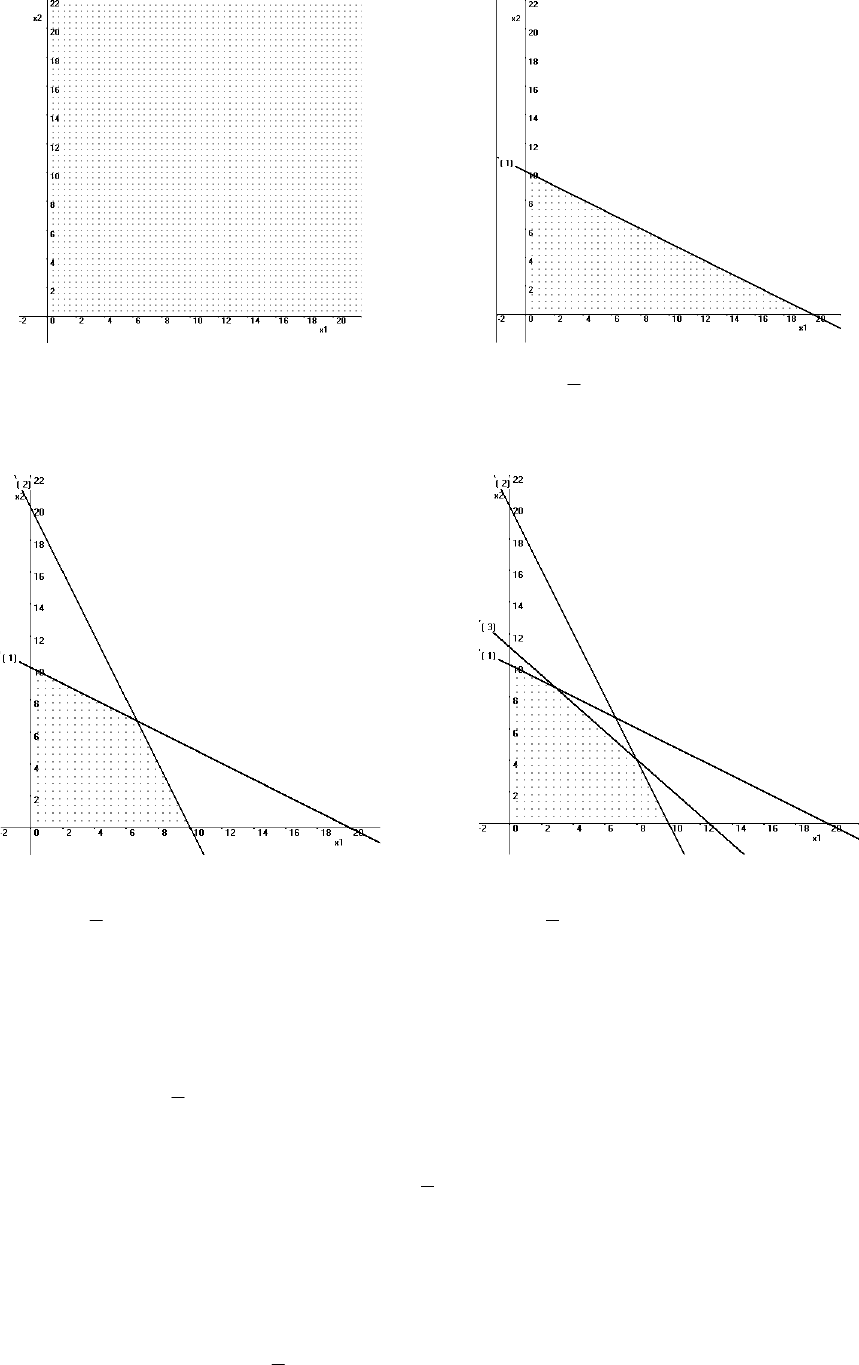
Их последовательное построение приведено ниже (Рисунок 5.1).
Область допустимых значений переменных находится в 1-м квадранте,
так как обе переменные могут быть только неотрицательными. Первая ли-
ния ограничений отрезает от 1-го квадранта всю область выше себя, так как
условие ограничения задано "меньше или равно". Вторая линия ограниче-
ний отрезает от уже выделенной области ту часть, которая выше неё, по-
скольку условие ограничения здесь задано также "меньше или равно". Тре-
тья линия ограничений отрезает от уже выделенной области ту часть, кото-
рая выше неё, поскольку условие ограничения здесь задано также "меньше
или равно".
В результате формируется область (помеченная внутри точками), огра-
ниченная сверху и справа линиями ограничений, а снизу и слева — условием
неотрицательности искомых переменных. Внутри этой области и должна
располагаться точка оптимума, соответствующая целевой функции.
86
а) исходная область допустимых ре-
шений переменных 0
1
x и 0
2
x
б) построение первого ограничения
2021)(
211
xxxq
Рисунок 5.1 — Последовательное построение области допустимых решений
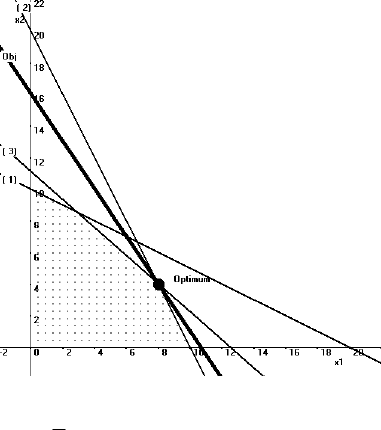
в) построение второго ограничения
6036)(
212
xxxq
г) построение третьего ограничения
4003632)(
213
xxxq
Рисунок 5.1 — Последовательное построение области допустимых решений
(продолжение)
Целевая функция в данном случае представляет собой прямую:
DxxxbxbxI
212211
2000030000)( . (5.6)
Чтобы её построить, необходимо в правой части вместо
D
задать какое-
то конкретное число. Устремление
)
(
x
I
к максимуму означает, что число
D
должно быть как можно бóльшим, но при том, чтобы
1
x и
2
x оставались в
области допустимых решений. Сразу определить это невозможно и требуется
первоначальная проверка при некотором начальном
D
, например, при
0
D
:
02000030000)(
21
xxxI
для которой строится прямая.
87
Затем следует проверить:
1) принадлежат ли найденные
1
x и
2
x области допустимых решений;
2) является ли значение
0
D
максимально возможным.
Если хотя бы одно условие не выполняется, то изменяют значение
D
,
вновь строят прямую линию целевой функции и вновь проверяют одновре-
менное выполнение указанных выше двух условий. Далее операции повто-
ряются до получения таких
1
x и
2
x , чтобы условия были выполнены.
Очевидно, что может потребоваться много проверочных построений,
чтобы найти окончательное решение. Задача существенно упрощается тем,
что целевая функция и ограничения — линейные выражения.
Линейность ограничений означает, что область допустимых решений
всегда будет представлять собой выпуклый многоугольник.
Линейность целевой функции означает, что при изменении
D
она будет
сдвигаться параллельно самой себе в ту или иную сторону. В частности, при
увеличении
D
она будет сдвигаться вправо вверх, а при уменьшении
D
—
влево вниз. При графическом решении задачи достаточно построить её один
раз, визуально определить направление желаемого перемещения и сдвинуть
параллельно самой себе так, чтобы она прошла через крайнюю точку области
допустимых решений (Рисунок 5.2).
Легче всего это можно сделать графически с помощью линейки.
Рисунок 5.2 — Построение целевой функции
21
2000030000)( xxxL
.
График целевой функции показан жирной линией (Рисунок 5.2). Для
рассматриваемого конкретного случая оказывается, что точкой оптимума яв-
ляется 8
1
x , 4
2
x , а целевая функция при этом будет:

88
320000800002400004200008300002000030000)(
21
xxxI ,
что означает следующее: если фирма произведёт 8 тонн первой краски и 4
тонны второй, то при существующих условиях она получит максимально
возможную прибыль 320 тыс. руб. При всех других вариантах прибыль будет
меньше.
Найденное решение можно использовать для дополнительного анализа
ситуации.
Во-первых, можно заметить, что имеющиеся запасы сырья оказываются
несколько излишними. Для производства оптимального количества красок
потребуется:
сырья С1: 16884281
22,111,11
xaxaC ;
сырья С2: 6012484386
22,211,22
xaxaC ;
сырья С3: 400144256436832
22,311,33
xaxaC .
Т. е. сырьё С2 и С3 израсходуется полностью (
max22
CC
,
max33
CC
), а
сырьё С1 израсходуется не полностью, при этом избыток сырья С1 составит
41620
1max1
CC тонны. Очевидно, при планировании производства
можно учесть это и закупить ровно столько сырья, сколько нужно.
То, что для двух видов сырья его использовано ровно столько, сколько
было в запасе, объясняется просто: точка оптимума лежит на пересечении
именно тех двух ограничений, которые связаны с этими видами сырья — С2
и С3, а первая линия ограничений (для сырья С1) проходит выше этой точки,
что и создаёт излишек.
Во-вторых, можно проанализировать, что будет, если начнут изменять-
ся цены, определяемые коэффициентами
1
b ,
2
b в целевой функции. Если они
будут одновременно и синхронно возрастать или уменьшаться, то это не
приведёт к изменению точки оптимума, так как соответствующая им прямая
будет перемещаться параллельно самой себе и не будет менять наклона, а по-
этому точка оптимума останется прежней. При этом будет меняться сумма
дохода, но всё равно он в данной точке будет наибольшим из всех возмож-
ных, т. е. объёмы произведённых красок будут соответствовать найденным.
Поэтому интерес представляет соотношение между ценами (коэффициента-
ми
1
b ,
2
b ):
2
1
b
b
или
1
2
b
b
, определяющее наклон линии целевой функции.
Если линию целевой функции зафиксировать в точке оптимума и начать
"качать" относительно неё, изменяя угол наклона, то она будет перемещаться

89
в пространстве между линией 6036)(
212
xxxq и линией
4003632)(
213
xxxq . Угол наклона любой прямой определяется ко-
эффициентами перед переменными
1
x и
2
x , которые в данном случае соот-
ветствуют цене соответствующего вида краски. Таким образом, соотношение
между ценами может меняться в диапазоне от 2
3
6
2
1
b
b
до
889,0
9
8
36
32
2
1
b
b
и при этом точка оптимума будет оставаться прежней,
т. е. соотношение между коэффициентами должно лежать в интервале
2
9
8
2
1
b
b
.
В предельных положениях линия целевой функции будет сливаться с
соответствующими линиями ограничений.
Можно также проанализировать, в каких пределах может изменяться
один из коэффициентов, если другой остаётся неизменным. Например, пусть
меняется цена на краску К1 (коэффициент
1
b ), в то время как цена на краску
К2 (коэффициент
2
b ) остаётся неизменной. Вопрос: в каком диапазоне может
меняться коэффициент
1
b , чтобы не нужно было изменять объёмы произво-
димых красок, т. е. чтобы не нужно бы менять технологический процесс, и
при этом достигался максимально возможный доход?
Нужно выразить один коэффициент через другой:
212
2
9
8
bbb .
Если зафиксировать коэффициент 20000
2
b , то интервал изменения
коэффициента
1
b становится следующим:
20000220000
9
8
1
b , 40000
9
160000
1
b , 4000078,17777
1
b .
Если цена краски К1 будет выходить за эти пределы, то необходимо пе-
ресчитать точку оптимума и определить новые оптимальные объёмы красок.
Этот результат можно понимать как анализ чувствительности оптимума
к параметрам целевой функции (к ценам).
При этом найденные оптимальные значения переменных останутся
неизменными: 8
1
x , 4
2
x , но величина общего дохода будет разной.
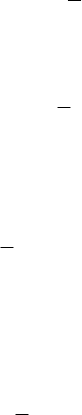
90
При наличии только двух переменных задачу можно легко решать гра-
фически, но уже при трёх переменных графическое представление должно
быть в пространстве и оперировать придётся поверхностями, что делает не-
возможным графический поиск решения. Реальное количество переменных
может исчисляться сотнями и тысячами. Для решения таких задач использу-
ются математические (алгебраические) методы.
Характерным для ЛП является то, что оптимальной оказывается одна из
крайних (угловых) точек области допустимых решений. Таких точек может
оказаться много (их число определяется количеством ограничений) и не все-
гда понятно, какая из них будет оптимальной. Поиск такой оптимальной точ-
ки и является задачей ЛП. При небольшом количестве ограничений можно
просто перебрать все имеющиеся точки, вычислить значение целевой функ-
ции в каждой из них и выбрать набольшее (если она максимизируется). Но
при большом числе ограничений получается много точек (тысячи, десятки и
сотни тысяч) и полный перебор может потребовать много времени. Поэтому
задачами ЛП является минимизация количества вычислений. Для этого раз-
работано много конкретных методов.
5.2 Формальная постановка задачи линейного программи-
рования
Задача линейного программирования формально выглядит следующим
образом:
для вектора в области действительных переменных
T
n
xxxx ),,,(
21
необходимо найти такие значения
T
n
xxxx ),,,(
21
,
при которых будет достигаться экстремум (максимум или минимум) целевой
функции
extr
2211
nn
xcxcxcxI
,
где
i
c — весовые коэффициенты целевой функции (действительные числа),
при выполнении системы ограничений типа равенств:
k
n
i
iikk
bxaxq
1
,
,
m
k
,...,
2
,
1
,
системы ограничений типа неравенств "больше или равно":
