Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.

ють, розв язуючи умовні рівняння корелат першої і другої

груп:

Vi -- v't -f- v{'.

Як відомо, середня квадратична помилка тf функції врів

новажених величин визначається за формулою

- у Рр ’

де ji — середня квадратична помилка, що відповідає одиниці

ваги, Рр — вага заданої функції врівноважених величин.

Середня квадратична помилка ц одиниці ваги визнача

ється за формулою

гИ

де r-\-t — кількість умовних рівнянь першої і другої груп.

Для визначення величини/^необхідно функцію (76,1) ви

разити через безпосередньо виміряні величини. Для цього

спочатку розкладемо її в рядок Тейлора, обмежуючись при

розкладанні членами з малими поправками v в перших сте

пенях:

/Г(1+'У1, 2-\~v2, ..., п-\-v„) — F(l, 2 ,..., я) + £Гїг,і

, dF

. .

дГ

+62

або

F — 1~^Ч ^ 1"Ь^2 ’V2-\~ • • • ~І~^Л “У/і, (76,2)

де для скорочення записів введено такі позначення:

^(І+г»!, 2+г»2, n + vn)=---:F,

F (\,2,..., n)—--F0,

др _ і

дї ~

де і =~ 1, 2,... , п.

Але Vi =vi' + v/', а тому функцію (76,2) можна записа

ти так:

F— F0-jr^i ’Vi,-\-\2v2

^-\lv ”-\-'k2v2-\-...-\-knVn- (76,4)

Первинні поправки v{ і вторинні v" залежні між собою,

а тому виключимо їх. Для цього скористуємося рівняннями:

Vi '= (її kx ■+- bi k2-\~ .. .-{-г* kr ,

Vi Аі Кі+Ві К2-1-.. .+ 7’і Kt .

/ W 0+[a>.] k^[bl] .. + [rX] kr -f-

+ [ЛХ]^+[ДХ] K3+. . .+ [П ] Kt . (76,5)

Корелати також залежні між собою, а тому виключимо і

їх. Для цього скористуємося -нормальними рівняннями (74,17)

і (74,18). Помножимо їх на неозначені поки що множники

■^[,^2

......... пг і II,, ІТ3, ..., п, відповідно і добутки додамо

до рівняння (76,5). Після очевидних перетворень будемо

мати:

F = F0-(-{[аа]^ і + [аЬ\%л - f - . •. + [аг]тс, + і

-Ь [ЬЬ]х2 -\-[Ьг\т.г -f- [йХ]}&2-р

+ { [ а г ] 1 ч +

[ Ь г \ ъ 2

- } - • • • +

[ г г ] к г

- ( - | r X ] } & , . - |~

+ {[ЛЛ ]П 1+ [ Л 5 ] Т І 2+ . . .+ [АТЩ( + [Л а ]}/ С ,+

+ { [Л В] II, -f [ВВ] П2+ . . . + [В T[llt + ІД Х ']К2+

................................................................................... (76,6)

г {[Л7]иі+|5 7'|ІІ2+ ...+[7’Г]П, +[7Х]}/С, +

+ W a T4 -\-W b т :,- |- . .-\-W r ъ г -f-

-\-W1\ll+ W 2U,+... \~Wt JI, .

Користуючись .неозначеністю МНОЖНИКІВ r.u IT,, . . т:г І llj,

ІІ2, .. ., П< , підберемо їх так, щоб вирази у фігурних дуж

ках дорівнювали нулю, тобто припустимо, що

[аа]і•[-{- [аЬ]т.2 -J-.. .-\-[аг\кг -}-[аХ]=0,

[ftft]n2 -j-.. ,-|-[fer]i:r —f—[£>X]=0,

.......................................................................... (76,7)

[ar\iti+ [ftr]ir2+ . . . + [rr]^+[rX ]=0;

[ЛЛ]1І1+ [Д £ ]П ,+ ...-Н Л 7 1 П / + И Х ]= 0 ,

[ЛВ]П, + [ДЯ]П2 + ...+ [£ 7] П, +[£Х] =0,

................................................................................ (76,8)

[Л7']1І1+ [£Г]П2+...+[7Т]ІІ, + [7Х]=0.

Тоді одержимо вираз заданої функції через величини

Юа, ъ'ь , . ■ •, wr і Wlt Wo,.. ■, Wt , які безпосередньо зв’язані

з результатами вимірів 1, 2, ... п:

F=F0-\-wa r,r y-wb ТС2+ . .. -\-WrT.r-\-

+ WlH1+ W 3Tl2+ ...+ Wt Jit. (76,9)

Щоб знайти обернену величину ваги цієї функції, засто

суємо відому з теорії помилок формулу

1 (dF\2 , (dF\2 . . (dF\i

/ ^ = b r ) 6+ b n ) 0+ - ,-+U 7/V (76, ю)

Враховуючи ті зауваження, які ми робили при визначенні

наш функції врівноважених величин при врівноваженні умов

них вимірів (див. §68), легко помітити, що часткові похідні

функції (76,9) матимуть такий вигляд:

дР

ді

^ = л2+ а ат:1+ ^ 2+ ." + г гН, + А 3П ,+ а д + ... 4- В Д ,

’..........................................................................................................................(76,11)

п -\~ап %іЛ~Ьп т"і 4- • ■ .-f-fп -|-А п Н і 4- Вп П а-(- .. ,-[-7'пП< .

Введемо позначення:

it:j —j— і lt2- [-Г^ ■— Aj,

Х2 + й2 TCj—)—£?3 rc2--J-.. .-(-Г2 Kr — Л2,

■ ■ ~l~^nT-r =A„.

(76,12)

Після підстановки цих позначень в (76,11) одержимо част.

нові похідні функції в такому вигляді:

^=Aj-j-,4] II, + в, П24 ... \-Tillt ,

%=Aa+ A 3lll-\Bi nt+...±TiUt . {76і13)

^ = А „ + / \ , 1 і і 1+ / Л і112+ . . . + 7 ’п11,

Згідно з формулою (76,10) знаходимо суму квадратів рів-

ностей (76,13):

-р-р = [ЛЛ]-|-{[^Л] П1 + [Л5]П2+ ... + И7-]П/ +

+ [ЛЛ]}ІІ1 +

+{[АВ] Ъ1+[ВВ]Пг+...+ [ВТ] П, +

+ [ВА]}Па +

.......................................................................................................... ( 7 6 ,1 4 )

+{ [Л7']П1+[Я7ІП2+...-|~[7Т] Ш +

+ [ Г Л ] } П , +

+ [ЛЛ] Г І^ ^ Л ] На+ ...+ [7’А]П< .

Доведемо тепер, що вирази в круглих дужках дорівню

ють нулю. Для .цього помножимо рів'няння (76,12) спочатку

на відповідні At, потім Bt і т. д. і нарешті на Ті . Підсумовую

чи кожен раз добутки і беручи до уваги умови (74,16), ма

тимемо:

[ЛЛ]=[ЛХ],

[ВЬ) = [В\],

.................... (76,15)

[ГЛ] = [ГХ].

Якщо замінимо тепер у рівнянні (76,14) величини [ЛА]

[5А], , [7’А], які стоять у фігурних дужках, через [ЛХ]

[fiX], [П] відповідно і порівняємо вирази в дужках з

рівняннями (76,8), то побачимо, що вони дійсно дорівнюють

нулю. Отже, формулу (76,14) можна записати так:

^= [А А ] + [ЛА] П1+[ДА]И2+ ...+[7’А]П/ . (76л6)

Нагадаємо, що цю формулу для визначення оберненої ве

личини ваги функції можна привести до такого остаточного

виду:

1 — [АЛ-а-ГААІ ИАГ-Лал-1]* .[ГА-р-р]»

pF Ілл гі [АА] [BS-1] "• [7'7'-(t—І)] (76,17)

і обчислення величини проводити в схемі Гаусса—Дулітля

одночасно з розв’язуванням иормальних рівнянь корелат, що

відповідають умовним рівнянням другої перетвореної групи.

Для обчислення за формулами (76,12) величинА^Лз,

які можна назвати перетвореними ваговими коефіцієнта

ми, необхідно знати неозначені множники іг,,іг2,...,vr, для чо

го в свою чергу треба розв’язати систему рівнянь (76,7).

Але коли при врівноваженні умовні рівняння поділити на

дві групи і до першої з них віднести ті рівняння, які не ма

ють спільних поправок і в яких коефіцієнти при поправках

рівні одиниці, то система рівнянь (76,7) набере такого ви

гляду:

п\ xi + [Чі = о,

П2 4" Мг — 0.

Пг Тсг-Ь [X], — 0,

звідки

ш,

■ Пі’

Мі

(76,18)

Пг ’

де ns — кількість невідомих поправок, які входять в умовне

рівняння першої групи з номером s = 1, 2, 3

..........

г; [Х]Л

сума вагових коефіцієнтів по s-й секції.

• Підставивши значення (76,18) ,в рівності (76,12), будемо

мати:

Л •, [> •]«

s\ t = s\t ~±А-. (76Л9)

З цієї формули видно, що вагові коефіцієнти Х(. перетво

рюються за тим самим правилом, що й коефіцієнти умовних

рівнянь другої Групи а і , Р/ , . . . , X/ .

Якщо рівності (76,12) помножимо спочатку на відповід

ні аь потім bі і т. д. і нарешті на г,- і кожен раз будемо скла

дати добутки, то, беручи до уваги (76,18), одержимо такі

співвідношення:

[аА] = [аХ]-)-[аа]т:1-|-[ай] іг2-|-.:.+[аг] іс, = 0,

[йА] = [*Х]+[а&] *,-+ [bb] + ...+[йг] = 0,

[гЛ] = [гХ]+[аг] [гг]г:, =0,

або

[Л]і = 0, [Л]а = 0,..., [Л]г=0.

(76,20)

Ці формули служать для контролю обчислень перетво

рених вагових коефіцієнтів.

§ 77. ВРІВНОВАЖЕННЯ ТРІАНГУЛЯЦІЙНОЇ СІТКИ

ДВОГРУПОВИМ МЕТОДОМ

(ЧИСЛОВИЙ ПРИКЛАД)

Прослідкуємо техніку застосування двогрупового методу

на числовому прикладі врівноваження тріангуляційної сітки.

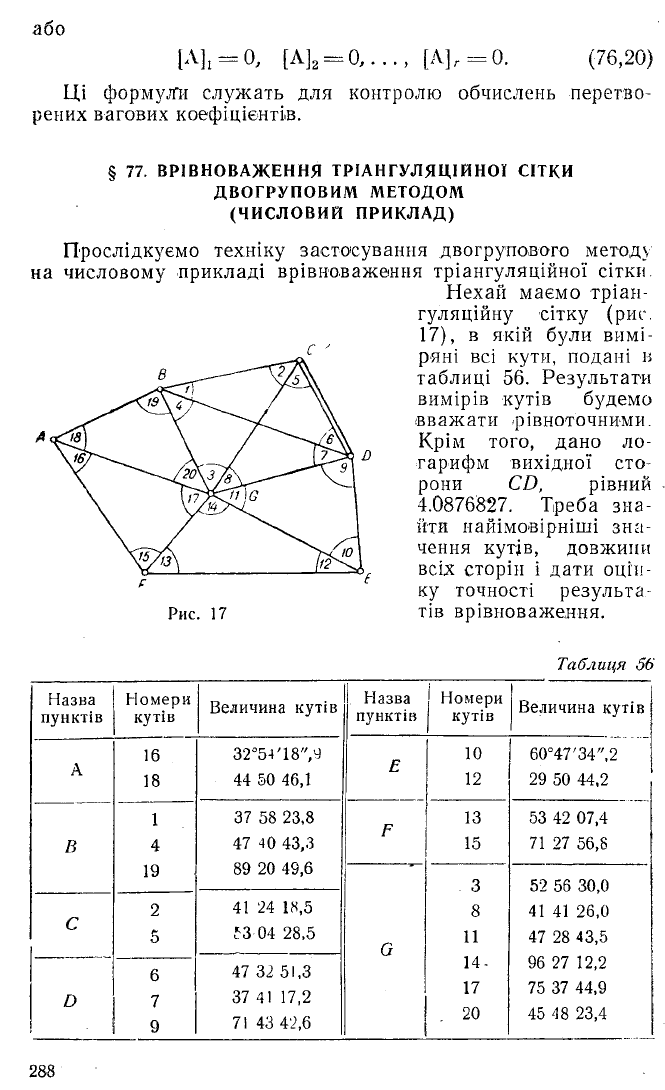
Нехай маємо тріан

гуляційну сітку (рис.

17), в якій були вимі

ряні всі кути, подані в

таблиці 56. Результати

вимірів кутів будемо

вважати рівноточними.

Крім того, дано ло

гарифм вихідної сто

рони CD, рівний

4.0876827. Треба зна

йти найімовірніші зна

чення кутів, довжини

всіх сторін і дати оцін

ку точності результа

тів врівноваження.

Таблиця 56

Назва

пунктів

Номери

кутів

Величина кутів

Назва

пунктів

Номери

кутів

Величина кутів

32°54'18",9 10

60°47'34",2

44 50 46,1

29 50 44,2

37 58 23,8 13

53 42 07,4

47 40 43,3

71 27 56,8

89 20 49,6

52 56 30,0

41 41 26,0

41 24 18,5

53 04 28,5

11 47 28 43,5

47 32 51,3

37 41 17,2

71 43 42,6

14-

96 27 12,2

75 37 44,9

45 48 23,4

У цій тригонометричній сітці всі врівноважені кути по

винні задовольняти 10 умовних рівнянь: 7 умовних рівнянь

трикутників (фігурних), 1 умовне рівняння горизонту і 2

полюсні умовіні рівняння. Це такі рівняння:

1. (1 )+ (2) +

2. (5 і+ (6)4- (7)

3. (9) + (10) + (11)

4. (12) + (13) + (14)

5. (15) + (16) + (17)

6. (18) + (19) + (20)

(3) + (4) + = 0

(8) + w2 = 0

+ ws = 0

+ wi = 0

+ да5 = О

+ Щ = О

І група (77,1)

7. (1) + (2) + (5) + (6) +«>а = О

8- (3) + (8)+(11) + (14) + (17) + (20) +та»э = 0

9. Д^2) + АП(6) + Д8 (8) + Д4 (4) -

~ M l ) - М 3 ) - Д6 (5) - А. (7) + wr = О

10. _Д2(2) +Д 6+7 (6) + Д6+7 (7) + Д 10 (Ю) +

’ (13) + д1в (1 б)+д19 (19) - Д1+4{(1 )+ (4 )}-

— ^ б (5 ) Д э(9) — ^ іг(1 2 ) — Д із(1 5) — Д 18 (1 8 )+ ге /5 = 0

гру

па

(77,2)

_ (1), (2),... — поправки до виміряних значень кутів; Д/ —

зміни логарифмів синусів кутів при зміні кута на одну се

кунду; W1, Wi, .. ., w„ — вільні члени умовних рівнянь пер

шої групи; Wa,W$, ,Wa — вільні члени умовних рівнянь

поправок другої групи. Умовне рівняння горизонту (8) ста

вить вимогу, щоб сума врівноважених кутів при центральній

точці G дорівнювала 360°. Введенням полюсного умовного

рівняння центральної системи (10) досягається виконання

умови, щоб довжина будь-якої сторони сітки, яку можна

обчислити двома різними шляхами, починаючи від вихідної

сторони, спочатку через один рядок трикутників, а потім че

рез другий, була однакова.

Геометрична суть решти умовних рівнянь нам уже ві

дома з попереднього викладу.

Всі умовні рівняння поправок поділені на дві групи, при

чому в першу групу входять ті умовні рівняння, однакові по

правки в яких не зустрічаються і коефіцієнти при яких до

рівнюють одиниці.

Всі обчислення по врівноваженню проводимо в таких

схемах.

. Розв’язування трикутників

ьс

о»

о ** в»

гм 00 со —'

05 со О N

СО 50 сп ю

СМ 0 5 ю

СО ТҐ со

СП со эо со

см О *—•

«з

ffi

ва

о,

* | ® “

» f s &

з к

>•»

Он

яи£л

игізиоя

НИГПСІЗй

ряєвц

я;хині^хи(Іі

udawoH

CO CO C l

с-. — г-

ГГ ю —•

С"> тГ О

00 О СМ

СП CN О

СП СО сл

0*0*0

со Ю со

s -ос N

05 оо ~

о — СО

С> Tf со

со СМ Ю

ю *-• см

00 ^ ю

О Ю СО

v СО

о о о о

+ 1 ^

* - ю о

N 00 О*

Р — СО

Ъ. со

со 'N Ю

LO — CN

00 ^ ю

-[ -С 4 СО

CQOO

М 1в е

«5 « «

со“

r-Г со N

.—Г

с о —" о

СО СО см 00 о с о —

СО 00 00

Ю со о

Ю СМ СО

СО

— Ю г-.

rf<

N C O S

со

’ t N ’t

со с о с о оо

см

о со о

см 1-І СМ О

см СМ *—' о

тг

•4-

... —

-------------------------

—

ь . СГ СО

1-» Ю —I

о> о>

N 0 0

СМ ОО СМ

О 05 см

ст. О 00

05 05 0>

оо г— Ю

О О ос

N t- ' ю

см о см

С'-' Ю т—<

Ю СО ТГ

N г— о

СО О со

о о ‘о

I + +

ю о ю

K Q C M

ю о ю

M O N

о —“о

I I I

со'

ОО

СО

СМ

см

Tt"

со

ю 00

о о

§11

8 *

UO-f-»

со

о с о

(NOO

см см

CO ^ 00

Ю О т р

N O N

N 4 * 0

0 5 05 OO

05 Oi Oi

ю со cm

if. tmCO

CM r F CO

^ CO ^

I—» © N

N ^o-t

Ю CO 00

o _ o о

сГо о

_l—1- I

ООО

CM r f СО

СО ТГ

° 4

О н

Q 4 0

■#4

« о н

«ф

f>T го —*

СО О ^

о- ю со

00 С—« ’— О

^ ^ ю

0 і

Ф ОО>

СЛ СМ СМ

со ^ ^

СО 0 5 f—

(МЮО)

со О со

<75 со (М

(O O N

О О С7І

со ОІ СП

со <о о

о —

O tM t4-

ю «а* см

О со со

см юаз

<£>со о>

О О О

о ' о" о ”

+ + 1

^ СО СО

<?. — о

cf сс" о“

*ф. 1-І‘

сЧ т*1сі

wO —

о>со <о

CN іС СГ)

00 со

со” Ч.

о со

O ' f

о ь ю

iO со «м

гг t“-.

SO оо

■•с Tt* ю

СО О «Ф

(NOC4

СС СМ »-•

а> о ю

4500)

со о о

со Ю «О

t"" СО 00

СТ. J5

го со CN

СОЬ

со 00

Ю —• vt<

С"- •*+ !>•

CN Ю СО

— О) to

СО N

ю со со

О О О

о “ сГ О о

+ + 1

О О О

СО t - г-

о о о

см см см

о o'" o '

I I I

(N fO ^

S i

00 05 05

5 00“ n*

) ~ ^

N ' t s

CN Ю ^

м С'ІЮ

t*** СО о»

о о

S -1-

о ї

2 a

Ї-

»+ с- м •* « Л -в»

см

ссГо <0

сТ

<V-* ^

О СО 1^ 00 (M O N

N 05 со 05 СО N іО

со

05 to —*

СО м ю

СО

rf<OCM

00 to

со

00 СО 05

05 СС 05 со

см о см о

см о см —

«ф ■44 'ф ^

rf ^

—

.....

....

—

CO CO CO

CO — CO

.— f " '

ССОЮ

0ОФЮ

tJ< 05 lO

00 0**0о

Ю —

•ФО) <0

CO 05 CO*

vf- ф CM

о О сс

IQ м

«- 05 Ю

'Ф со

ІС Ф О

О О О

о о" о

+ 4- I

О О О

vr^O О-

с£'аГсо

-Ф см

t'- '

со >■«* со

сс ю

О со СЛ

а> со о -

СО О СО

ЬО>0О

os а> 05

Ю СО СМ

<М Ої 00

rj** lO оГ

СМ 'Ф

CO со см

Ю СМ СО

r^. rt-

СО О

iO CM СО

cO ^ C-~

о" r-Г о*

I I I

о о о о

со со со о>

о o ' о ' р

•і І- і- ! ■

се CD со

rf -ф СМ

О О оо

|Q CM

'Ф О О 'Ф

CO O i о

— г— см

05 о

ю .

05 1

Ю II

iO v

СО I

ПГГ^,<

СМ -«4* I

CON^

см »о

00 оо см

ЮСА 00

t"". тГ Г"»

со 03 ^

СО

0 ,0 'Л

«>00 I

см см"

® - к

. ./

ГЧ -{-СО

см

eqtjQ

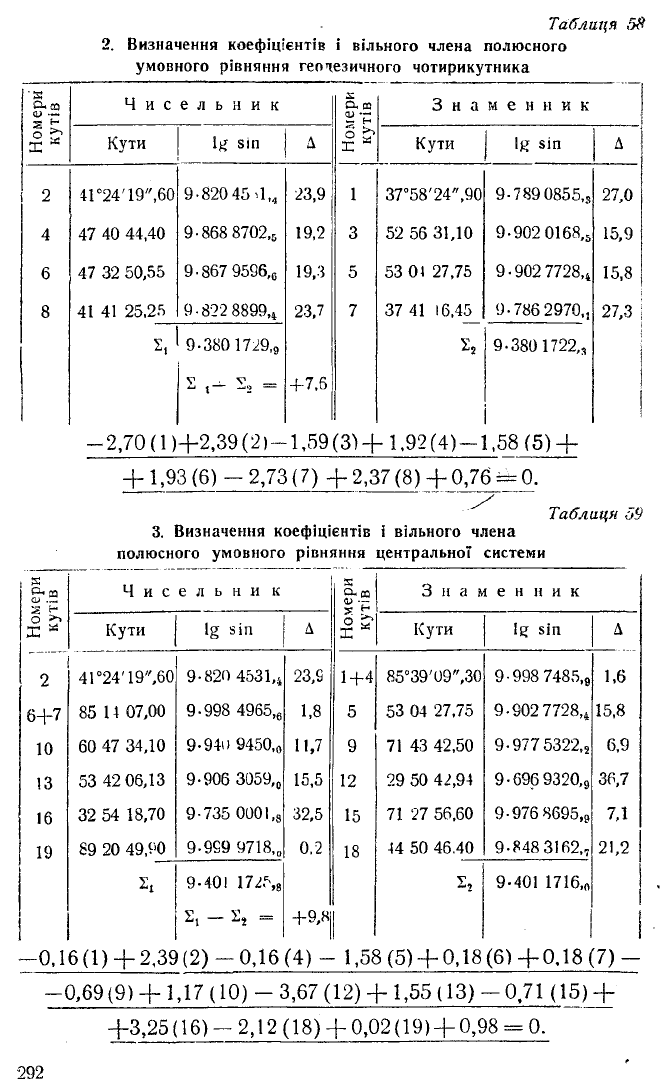
Таблиця 58

2. Визначення коефіцієнтів і вільного члена полюсного

умовного рівняння геодезичного чотирикутника

' 3

О* CQ

О)

Ч и с

ельник

О, ю

£ н

3 н а

м е н н и к

J и

Кути

lg sin Д

о ^

Г “

Кути ig sin Д

41°24'19",60

9-820 45 '1,4

23,9

1 37°58'24",90 9-789 0855,.,

27,0

47 40 44,40

9-868 8702,5 19,2

3 52 56 31,10 9-902 0168,5

15,9

47 32 50,55

9 • 867 9596,0

19,3

53 01 27,75 9-902 7728,4

15,8

41 41 25,25 9-822 8899,4 23.7 7

37 41 16,45 9-786 2970,,

27,3

9-380 1729,9

V V

“ і -а —

+7,6

9-3801722,з

-2,70 (1 )+2,39 (2)-1,59 (3) + 1,92 (4)-1,58 (5) +

+ 1,93 (6) -2,73(7) +2,37(8) + 0,76 = 0.

Таблиця о9

3. Визначення коефіцієнтів і вільного члена

полюсного умовного рівняння центральної системи

Л CQ

Ч и с

e л ь H и к

Номери :

кутів j

Знаменник

X *

Кути

lg sin

Кути

ІЕГ sin

41°24'19",60

9-820 4531,4

23,S

1+4

85°39'09",30 9 • 998 7485,9

1,6

6+7

85 14 07,00

9-998 4965,e

1,8 5

53 04 27,75

9-902 7728,t 15,8

60 47 34,10

9-940 9450,0

11,7

71 43 42,50

9-9775322.J 6,9

53 42 06,13

9-906 3059,0

15,5

29 50 42,94

9-696 9320,9

36,7

32 54 18,70

9-735 0001,8

32,5

71 27 56,60

9-976 8695,9

7,1

89 20 49,90

9-9S9 9718,,,

0,2

-14 50 46.40

9-848 3162,,

21,2

9-401 172.%8

2 , — =

+9,8

9-401 1716,0

—0.16(1) + 2,39(2) - 0,16 (4) - 1,58 (5) + 0,18(6) +0,18 (7) —

—0,69(9) + 1,17 (10) — 3,67 (12) + 1,55 (13) — 0,71 (15) +

+3,25(16) — 2,12 (18)+ 0,02 (19)+ 0,98 = 0.