Carlip S. Quantum Gravity in 2+1 Dimensions

Подождите немного. Документ загружается.

226 Appendix A

so the deck transformations give an action of m(M) on M. This action

can be shown to be free and properly discontinuous. It is then evident

that the quotient M/n\(M) determined by this action identifies all of the

points yi G M lying above any given point x G M, thus collapsing M

down to a single copy of M, verifying (A.

13).

A.7 Geometrization

Quotient spaces as we have defined them are topological constructs, but

it is often possible to add additional structure. For example, if M has

a Riemannian metric and G is a group of isometries of that metric,

then M/G will inherit a metric; if M is a complex manifold and G acts

holomorphically, M/G will inherit a complex structure.

In two dimensions, one of the fundamental results of Riemajnn surface

theory, the

uniformization

theorem,

makes use of this fact. Let C = C

U oo

be the Riemann sphere, with its standard metric of constant curvature

+1,

4dzdz

d (A15)

let C be the complex plane, with its standard metric of constant curvature

= dzdz; (A.16)

and let H

= {z

Imz > 0} be the upper half-plane, with its standard

metric of constant curvature

—1,

It can be shown that every surface is homeomorphic to Z)/F, where D is

either C, C, or H

and F is a properly discontinuous group of isometries

of the constant curvature metric on D. This means that every surface

admits a constant curvature metric, and that the classification of such

metrics may be reduced to an algebraic problem of classifying groups of

isometries of a few covering spaces. We thus obtain a fruitful connection

between topology, geometry, and algebra.

An important open question is whether this idea can be extended to

three-dimensional manifolds. As in two dimensions, there are a small

number of 'geometric' three-manifolds that can occur as covering spaces.

Thurston's geometrization conjecture is that any three-manifold can be

decomposed into pieces that are quotient spaces of one of these geometric

Cambridge Books Online © Cambridge University Press, 2009

The topology of manifolds 227

Fig. A.3. A triangle is subdivided by inserting an additional vertex and three

additional edges. See figure 11.3 for the subdivision of a tetrahedron.

manifolds (the exact definition of 'decomposition' is a bit complicated).

This conjecture has been shown to hold in a large number of special cases,

but a general proof is still lacking

[257].

A.8 Simplices and Euler numbers

To understand (2+l)-dimensional gravity, we shall need one more key

topological invariant, the Euler number of a manifold. Let us start with

a simple example, a two-dimensional surface. Any surface 2 can be

triangulated, that is, broken up into a set of triangles joined along their

edges (see figure 11.1). Given such a triangulation, the Euler number x of

2 is defined as

where F is the number of faces, E is the number of edges, and V is the

number of vertices in the triangulation.

It is not too hard to show that #(2) depends only on the surface 2, and

not on the triangulation. This can be made plausible by considering the

effect of subdividing a triangle (see figure A.3): the subdivision introduces

two new faces, three new edges, and one new vertex, thus leaving x

unchanged. It is also clear that #(2) is a topological invariant of Z, that

is,

that it is preserved by homeomorphisms.

To generalize this construction to higher dimensions, we first need the

p-dimensional generalization of a triangle. Given a set of p + 1 linearly

independent vertices {xi,...,x

+i} € R

, a p-simplex o

is the set

{

i=i >=i

The jth face of o

is the subsimplex {x e a

Xj =

0}.

A simplicial complex

Cambridge Books Online © Cambridge University Press, 2009

228 Appendix A

is a set of simplices joined along common faces, or more precisely a set

K of simplices satisfying the following conditions:

K, then all of the faces of o

are also in K; and

e K, then either o

n o

= 0 or o

D a

is a common face

of a

and a

The dimension of K is defined to be the maximum dimension of a simplex

in K. A triangulated surface, for instance, is homeomorphic to a simplicial

complex of dimension 2; a 3-simplex is a solid tetrahedron.

The Euler number of an m-dimensional simplicial complex K is defined

in exact analogy to the two-dimensional case:

(K) = f(-l^, (A.20)

p=0

where N

is the number of p-simplices a

in K. #(K) can again be

shown to be a topological invariant, and can therefore be defined for any

manifold homeomorphic to a simplicial complex. An important result is

that %(M) = 0 for any closed odd-dimensional manifold.

For dimension greater than two, the Euler number gives only limited

information about the topology. More powerful topological invariants, the

homology groups, can be built from simplicial complexes, but I shall not

discuss these here; see, for instance, [192] or

[204].

It is worth mentioning

that the choice of dividing a manifold into simplices instead of other

building blocks is somewhat arbitrary; for instance, a 'cell decomposition'

of a M into p-dimensional balls can also be used to determine the Euler

number and the homology groups.

The Euler number is important in part because of the Poincare-Hopf

index theorem, which relates x(M) to the properties of vector fields on M.

Let v be a vector field with a zero at some point x e M. The index of v

at x is a measure of the directional change of v around x, determined as

follows. Choose a neighborhood of x homeomorphic to R", and consider

a small (n

—

l)-sphere S

€

around x. The unit vector v/\v\ on S

€

can then

be viewed as a map from S

€

to the unit sphere, and the index of v at x is

defined as the degree of this map.* In two dimensions, the index measures

the number of times v rotates as we move counterclockwise around x; a

source has index 1, while a saddle has index

—1.

The Poincare-Hopf theorem states that if v is any smooth vector field

with isolated zeros on a compact oriented manifold M, and if v points

The degree is the number of times S

covers the unit sphere; for a precise definition, see

reference [76],

[192],

[196].

Cambridge Books Online © Cambridge University Press, 2009

The

topology

manifolds

229

-l

Fig. A.4. A torus may be cut open to form a parallelogram.

outward at each boundary component of M, then [196]

ind(v) =

where ind(v) denotes the sum of the indices of v at all of its zeros. In

particular, a vector field on a compact manifold with x(M)

=/=

0 must

have zeros. (This is the theorem that 'you can't comb a hairy billiard ball

without leaving a bald spot'.) Conversely, a vector field with ind(v) = 0

can always be deformed to one that vanishes nowhere on M. This will

be important in appendix B when we discuss the existence of Lorentzian

metrics on (2+l)-dimensional spacetimes.

A.9 An application: topology of surfaces

Let us now apply these ideas to the topology of two-dimensional orientable

surfaces. As noted above, any such surface is homeomorphic to either a

sphere S

or the connected sum of

tori. The number g is the genus; the

sphere is said to have genus zero.

It is clear that the two-sphere has a trivial fundamental group, that is,

that any loop on S

is contractible. S

is thus its own universal covering

space. To obtain its Euler number, note that S

is homeomorphic to the

surface of a tetrahedron. This surface is a simplicial complex with four

faces,

six edges, and four vertices, so by (A.

18),

/(S

) = 2.

Next consider the torus T

. Let us cut the surface open to form a

parallelogram P (figure A.4), with edges labeled A, J3, A~

, and B"

;

to recover the original torus, we sew together opposite edges, identifying

A with A~

and B with B~

. It is evident from the figure that A is a

noncontractible curve on T

, and thus represents an element of ni(T

represents the same curve traversed in the opposite direction, so as

a homotopy class it is indeed the inverse of A. Similarly, B and B~

represent another element of n\(T

) and its inverse.

The product AB is a spiral going once around the torus. Other noncon-

tractible curves can be obtained by taking more complicated products, and

Cambridge Books Online © Cambridge University Press, 2009

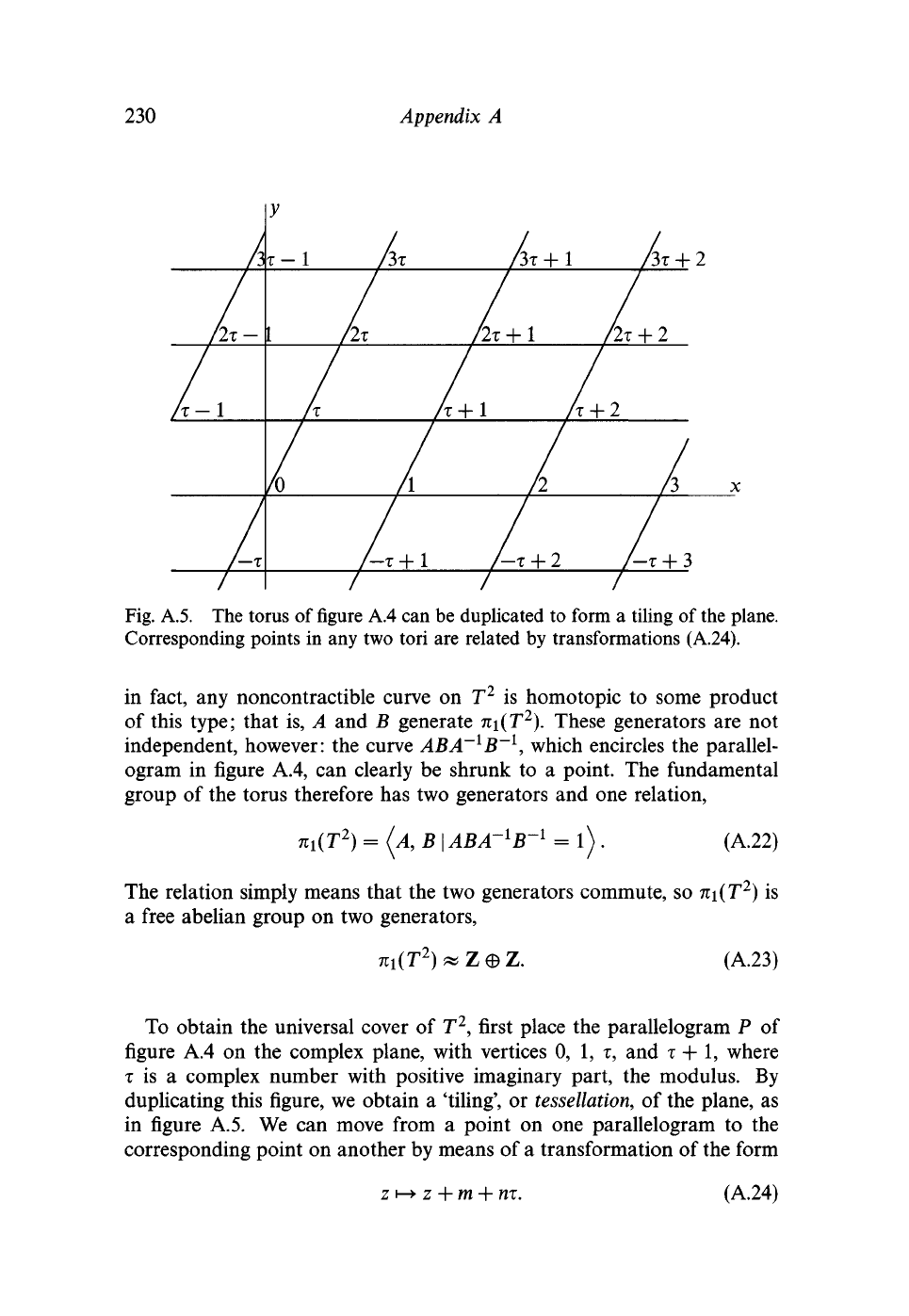
230 Appendix A

3T-1

i hi h

/ /,

/ /

+ 1

/2T

+ 2

/, ,

Fig. A.5. The torus of figure A.4 can be duplicated to form a tiling of the plane.

Corresponding points in any two tori are related by transformations (A.24).

in fact, any noncontractible curve on T

is homotopic to some product

of this type; that is, A and B generate n\(T

). These generators are not

independent, however: the curve ABA~

, which encircles the parallel-

ogram in figure A.4, can clearly be shrunk to a point. The fundamental

group of the torus therefore has two generators and one relation,

(A,B (A.22)

The relation simply means that the two generators commute, so

TCI(T

) is

a free abelian group on two generators,

~ 7 m 7 f A 1V\

M-A

\& JLJ. yr^..z*~) j

To obtain the universal cover of T

, first place the parallelogram P of

figure A.4 on the complex plane, with vertices 0, 1, T, and

+ 1, where

is a complex number with positive imaginary part, the modulus. By

duplicating this figure, we obtain a 'tiling', or tessellation, of the plane, as

in figure A.5. We can move from a point on one parallelogram to the

corresponding point on another by means of a transformation of the form

(A.24)

Cambridge Books Online © Cambridge University Press, 2009

The

topology

manifolds

231

These transformations describe a free, properly discontinuous action of

Z on C, and we can form the quotient space C/Z

Z. The transfor-

mation zi-^z +

identifies the edges A and A~

of P, while

ZHZ

identifies B and B"

, so the quotient space is simply the original torus,

and C can be identified as the universal cover of T

. Each parallelogram

in figure A.4 is a fundamental region for the group action.

This quotient space representation allows us to see the action of the

mapping class group of T

- also known as the modular group - quite

explicitly. Consider a Dehn twist around the curve B - that is, cut the

torus open along B, twist by 2n, and reglue the edges. This process will

clearly not change B, but A will be twisted into a spiral, A

i—•

AB. The

effect on the tiling of the plane will thus be to shift x to x + 1. A Dehn

twist around A is a bit harder to visualize, but its effect is to transform

T/(T

1).

These two transformations generate the mapping class group

of the torus; a more common, but equivalent, representation is given by

x -*

+ 1. (A.25)

We next consider the geometry corresponding to this quotient construc-

tion. A torus C/Z

Z will inherit a flat metric and a complex structure

from the plane. Tori obtained from parallelograms with different values of

x will all be homeomorphic, of course - any torus is homeomorphic to any

other - but in general, the homeomorphisms will not be isometries. Hence

different values of

will ordinarily label different flat metrics on T

. The

resulting parameter space {T G C : Imx > 0} is called the

Teichmiiller

space Jf of the torus.

Not all values of x give distinct geometries, however. We have seen

that diffeomorphisms in the mapping class group, which surely cannot

change the metric, do change

identify the values of

that differ by

transformations of the form (A.25), we obtain the true parameter space

of flat metrics on the torus modulo diffeomorphisms, the moduli space.

Points in moduli space are orbits of the mapping class group, which acts

properly discontinuously on Teichmiiller space; if

denote the mapping

class group by

the torus moduli space is the quotient space Jf = Jf

JQ).

A fundamental region for the group action is the 'keyhole' region shown

in figure A.6.

Finally, to obtain the Euler number of the torus we must find a trian-

gulation of T

. A suitable triangulation is shown in figure A.7, and by

counting simplices we see that x{T

) = 0.

We are now ready to tackle higher genus surfaces 2

. Just as a torus

can be cut open into a parallelogram, a genus g surface can be dissected

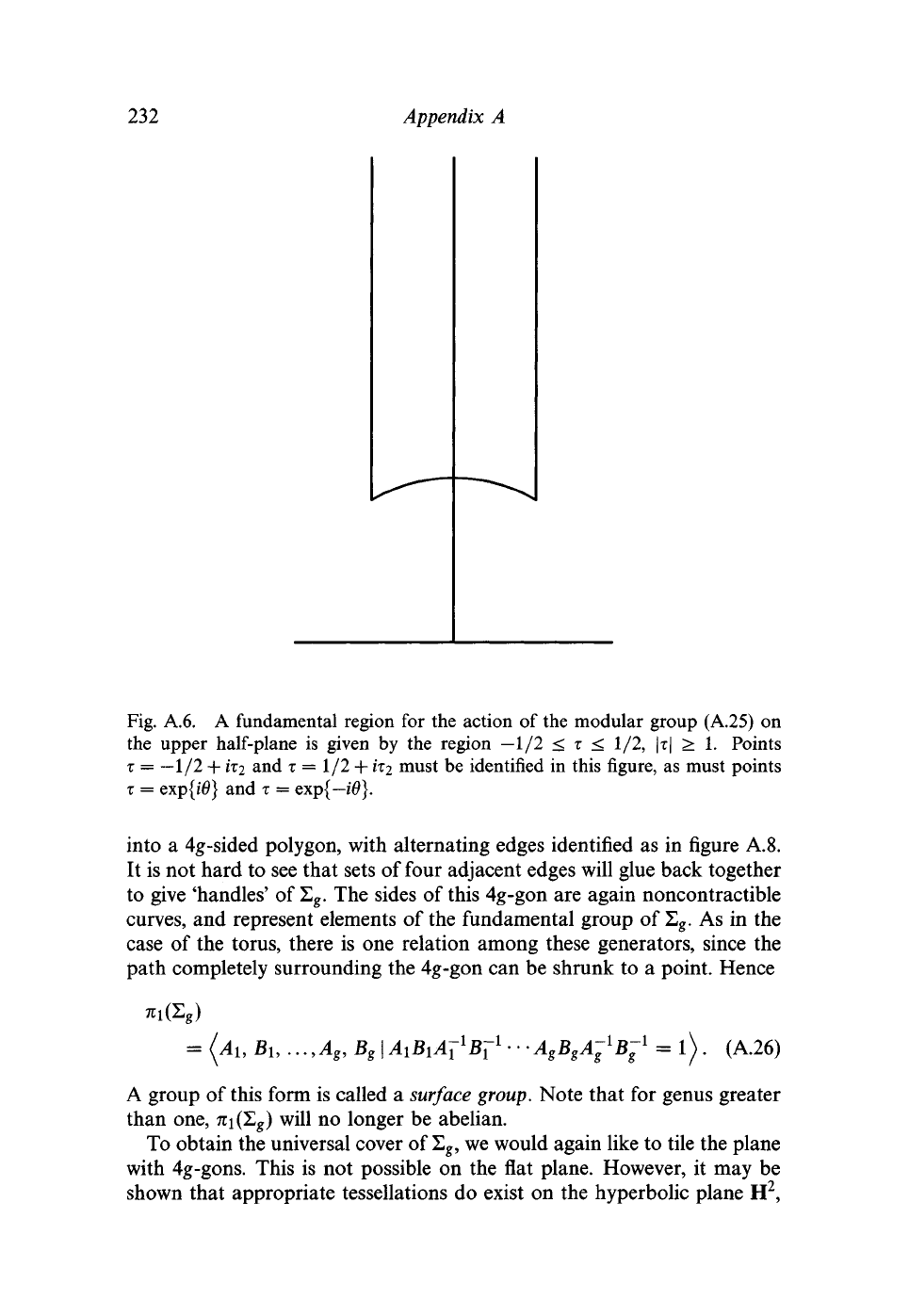
232

Appendix A

Fig. A.6. A fundamental region for the action of the modular group (A.25) on

the upper half-plane is given by the region —1/2 < T < 1/2, |T| > 1. Points

T = —1/2 +

iT2

and T = 1/2 +

I*T2

must be identified in this figure, as must points

= exp{i0} and

= exp{—i6}.

into a 4g-sided polygon, with alternating edges identified as in figure A.8.

It is not hard to see that sets of four adjacent edges will glue back together

to give 'handles' of S

. The sides of this 4g-gon are again noncontractible

curves, and represent elements of the fundamental group of

As in the

case of the torus, there is one relation among these generators, since the

path completely surrounding the 4g-gon can be shrunk to a point. Hence

= 1

(A.26)

A group of this form is called a

surface

group.

Note that for genus greater

than one, rci(E

) will no longer be abelian.

To obtain the universal cover of

we would again like to tile the plane

with 4g-gons. This is not possible on the flat plane. However, it may be

shown that appropriate tessellations do exist on the hyperbolic plane H

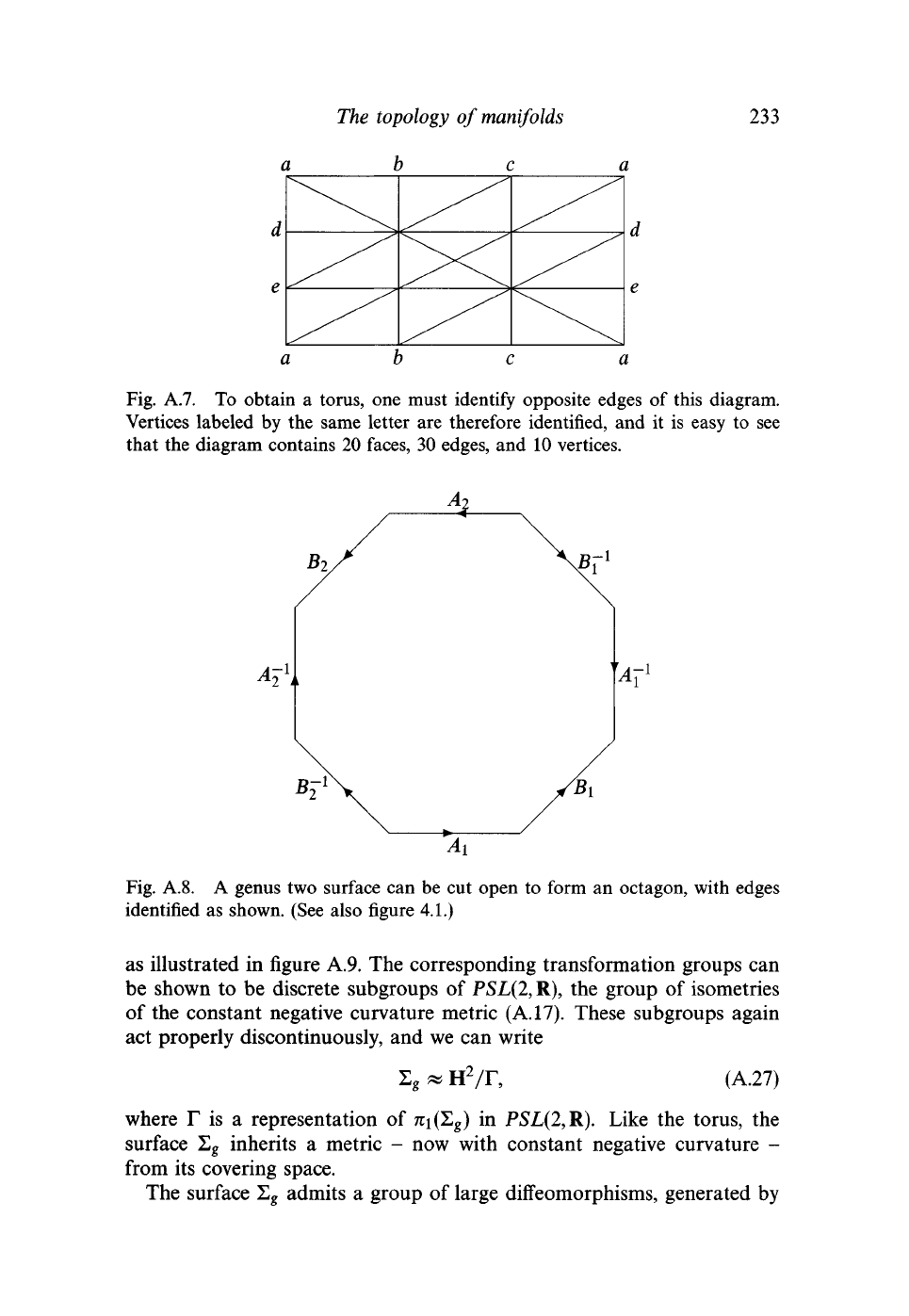
The topology of manifolds

a b c

233

Fig. A.7. To obtain a torus, one must identify opposite edges of this diagram.

Vertices labeled by the same letter are therefore identified, and it is easy to see

that the diagram contains 20 faces, 30 edges, and 10 vertices.

Fig. A.8. A genus two surface can be cut open to form an octagon, with edges

identified as shown. (See also figure 4.1.)

as illustrated in figure A.9. The corresponding transformation groups can

be shown to be discrete subgroups of PSL(2,

R),

the group of isometries

of the constant negative curvature metric (A.

17).

These subgroups again

act properly discontinuously, and we can write

Lg « rl /I ,

(A.z/j

where T is a representation of n\(L

) in PSX(2,R). Like the torus, the

surface Z

inherits a metric - now with constant negative curvature -

from its covering space.

The surface Z

admits a group of large diflfeomorphisms, generated by

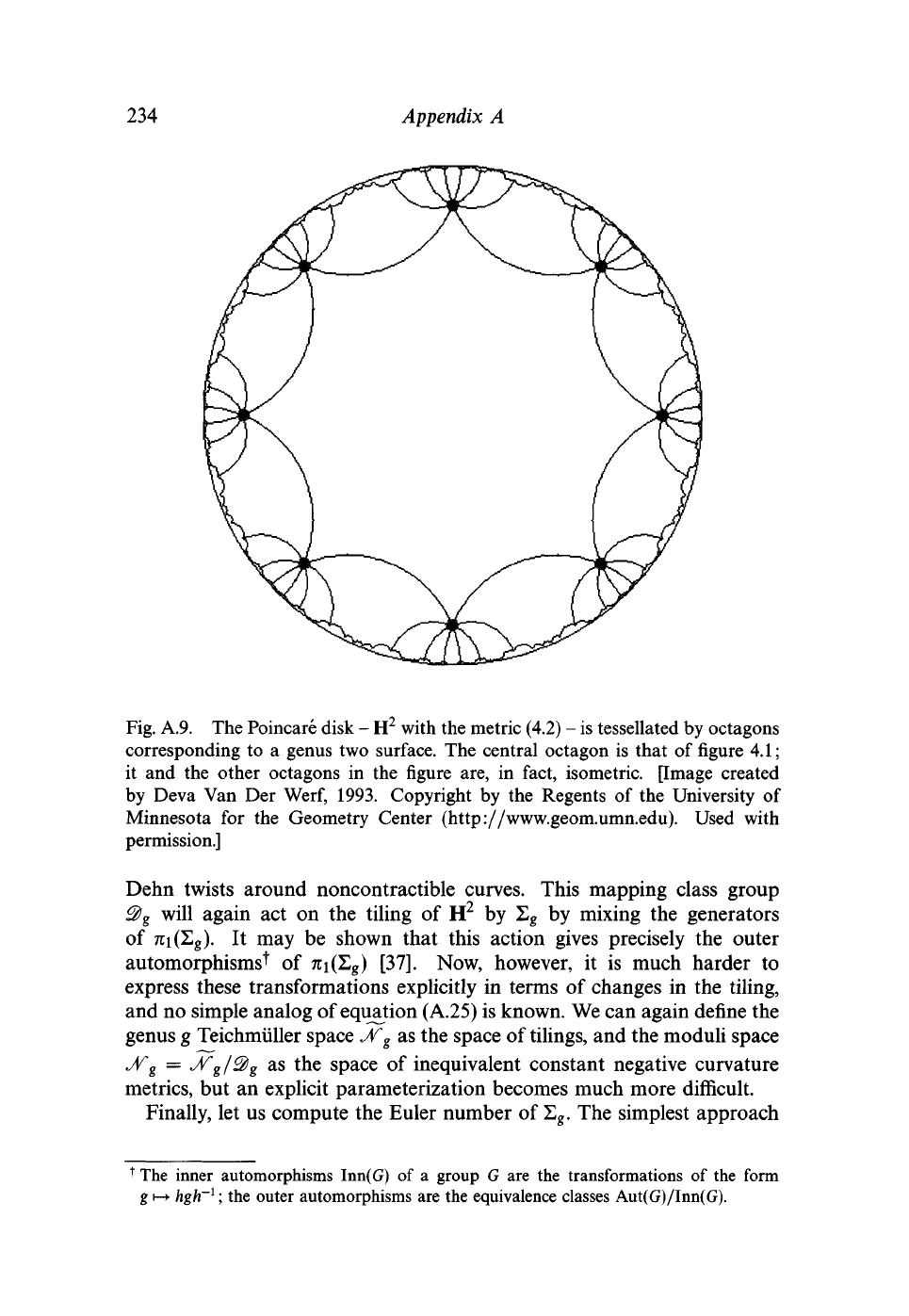
234

Appendix A

Fig. A.9. The Poincare disk - H

with the metric (4.2) - is tessellated by octagons

corresponding to a genus two surface. The central octagon is that of figure 4.1;

it and the other octagons in the figure are, in fact, isometric. [Image created

by Deva Van Der

Werf,

1993. Copyright by the Regents of the University of

Minnesota for the Geometry Center (http://www.geom.umn.edu). Used with

permission.]

Dehn twists around noncontractible curves. This mapping class group

will again act on the tiling of H

by S

by mixing the generators

of TTi(Sg). It may be shown that this action gives precisely the outer

automorphisms''' of n\(L

) [37]. Now, however, it is much harder to

express these transformations explicitly in terms of changes in the tiling,

and no simple analog of equation (A.25) is known. We can again define the

genus g Teichmiiller space Jf

as the space of

tilings,

and the moduli space

= jVg/Qjg as the space of inequivalent constant negative curvature

metrics, but an explicit parameterization becomes much more difficult.

Finally, let us compute the Euler number of 2

. The simplest approach

The inner automorphisms Inn(G) of a group G are the transformations of the form

g i-> hghr

; the outer automorphisms are the equivalence classes Aut(G)/Inn(G).

The

topology

manifolds

235

is to take advantage of the fact that £

« T

#£

_i, where # denotes

the connected sum. Given triangulations of S

_i and T

, we can form

the required connected sum by removing one face from each surface and

identifying three edges and three vertices. The lost edges and vertices

cancel in the Euler number (A.

18),

but the total number of faces is

reduced by two. Thus

g g

- 2, (A.28)

and using our previous result that x(T

) = 0, we see that

(A.29)