Chattaraj P.K. (Ed.) Quantum Trajectories

Подождите немного. Документ загружается.

244 Quantum Trajectories

states, in contrast, are delocalized, across a very large region of space. Thus, if these

states were computed directly for a large-D system, it would require prohibitive com-

putational effort, regardless of the method used. In any event, we seek a bipolar

version of the TDSE wavepacket propagation equations, presumably offering all of

the advantages discussed previously in the context of TISE solutions.

In addition to previous considerations, the bipolar wavepacket evolution equations

must satisfy:

• localized ψ implies localized ψ

;

• at initial time, ψ = ψ

is the incident wavepacket;

• at ﬁnal time, ψ

is the transmitted wavepacket, and ψ

−

the reﬂected

wavepacket;

• at all times, ψ evolution satisﬁes the TDSE.

For 1D systems, the above can be achieved via coherent superposition of sta-

tionary state solutions at different energies, applied separately to ψ, ψ

, and ψ

−

Speciﬁcally, let the TISE solution for energy E be henceforth referred to as φ

(x) =

(x) +φ

−

(x). Then,

ψ(x, t ) =



a(E)ϕ

(x) exp[−iEt/]dE, (15.7a)

where

a(E) =ϕ

|ψ(t = 0). (15.7b)

Applying the same expansion to the bipolar TISE components yields the correspond-

ing ψ

(x,t):

(x, t ) =



a(E)ϕ

(x) exp[−iEt/]dE. (15.8)

Substitution into Equation 15.6a then yields time evolution equations which—when

recast so as to avoid all explicit dependence on the underlying TISE solutions—result

in the following [24]:

∂ψ

∂t

=−







H ψ







(Ψ

− Ψ

−

)



(15.9a)

where

(x) =



−∞



)dx



. (15.9b)

The resultant bipolar wavepacket components, ψ

(x,t), behave exactly as indicated

above, i.e., for an initially left-incident wavepacket, localized far to the left of the

scattering barrier, ψ(t = 0) = ψ

(t = 0). Over time, as ψ

reaches the barrier, a

reﬂected ψ

−

component comes into being in the PES barrier region. The ψ

com-

ponent then continues to head to the right, turning into the transmitted branch of the

ﬁnal wavepacket, whereas ψ

−

heads to the left and becomes the reﬂected branch.

Bipolar Quantum Trajectory Methods 245

Note from Equation 15.9a that the intercomponent coupling is proportional to V



(x);

thus, coupling arises only in the PES barrier region, so that in the asymptotic regions,

both components satisfy free particle propagation.

For Equation 15.9 to be useful, ψ

should be smooth and interference-free for

all times. In general, it is extremely difﬁcult to concoct a bipolar theory that satisﬁes

this property, owing to the square-root relationship between ψ and ρ, which tends to

magnify the effects of interference. Nevertheless, Equation 15.9 achieves this goal

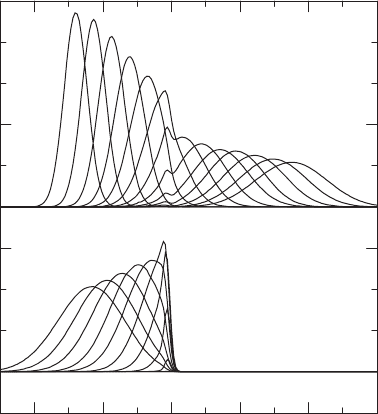
very well, for a wide range of applications [24]. Figure 15.5 depicts the time evolution

of the bipolar densities, ρ

(x,t), for a wavepacket scattering application (the symmet-

ric 1D Eckart barrier discussed previously). The bipolar components are smooth and

well behaved, even though ρ(x,t) itself exhibits substantial reﬂection interference—

accommodated in the bipolar treatment through the “spur” that develops on the back

end of ψ

, and ultimately vanishes in the large-time limit (a process known as “node

healing” [12]).

–10

0.9

0.6

0.3

0.0

Density

–5 0 5

Position, x

10 15

FIGURE 15.5 Bipolar component wavepacket densities, ρ

(x,t) as a function of position, x,

and for a variety of times, t, for the symmetric Eckart barrier system of Figures 15.1 and 15.4.

The upper family of curves represent ρ

(x,t) at different times, whereas the lower family of

curves represent ρ

−

(x,t) (magniﬁed by a factor of 4x). The motion of the former over time is

left-to-right, whereas that of the latter is right-to-left.At intermediate t, a stationary ρ

(x,t) spur

forms and then dissipates in the barrier region, corresponding with the simultaneous “birth”

and stationary growth of ρ

−

(x,t). After ρ

−

(x,t) has grown sufﬁciently large, it starts to move

to the left. (Reprinted with permission from Poirier, B., Journal of Chemical Physics, 128,

164115, 2008.)

246 Quantum Trajectories

Although not visible on the scale of the Figure 15.5 plots, the ρ

(x,t) plots actually

do exhibit very slight nodal behavior, in the asymptotic regions where the density val-

ues are extremely small. Thus, whereas the interference situation is greatly improved

in the bipolar case, it has not been completely eradicated. This may be due to the fact

that Equation 15.9, like Equation 15.6a, is based on the V

eff

(x) = 0 choice of effec-

tive potential. As discussed in Section 15.4, a more classical-like choice for V

eff

(x)

is probably more appropriate. At present, however, it is not known how to extend

the derivation of Equation 15.9 for arbitrary V

eff

(x), to obtain standalone bipolar

wavepacket evolution equations that make no explicit reference to the φ

15.6 WAVEPACKET SCATTERING DYNAMICS

IN MANY DIMENSIONS

Equation 15.9 can be easily generalized for multidimensional systems with arbitrary

(straight or curvilinear) reaction paths and coordinates. All that is needed is a speci-

ﬁcation of the reaction coordinate direction, ˆs, at every point in space, !x. The spatial

derivative in Equation 15.9a then gets replaced with ˆs ·

∇V , and Equation 15.9b with a

line integral along ˆs. With ψ

∆

= (ψ

− ψ

), the result is [25]:

∂ψ

∂t

=−









H ψ



ˆs ·

∇V



∆



(15.10a)

where

∆

(!x) =



−∞

∆

(!x + s ˆs)ds. (15.10b)

The many-D bipolar wavepacket propagation equations above have been applied to

a number of test applications [25], including the collinear H + H

chemical reac-

tion system in Jacobi coordinates, indicated in Figure 15.6. In all cases considered,

the resultant bipolar densities are smooth and well-behaved at all times, as well as

satisfying all of the other desired properties as discussed above.

15.7 NUMERICAL IMPLEMENTATIONS

For quantum scattering problems for which the bipolar component propagation equa-

tions are solved using conventional means, the resultant computed ψ

(x,t)’s can then

be used to obtain bipolar quantum trajectories. Such an “analytical” approach is often

applied in the pure Bohm QTM context to provide physical insight [33], and the same

has been done in the bipolar case for simple 1D model systems [27]. However, the

main interest here is for synthetic calculations, i.e., to propagate the bipolar quantum

trajectories without knowing ψ

(x,t) a priori. To this end, there are two basic types

of numerical implementations that have been considered: (1) exact numerical prop-

agation of Equations 15.6a, 15.9a, or 15.10a, via communicating (interdependent)

quantum trajectory ensembles; and (2) approximate numerical propagation, using

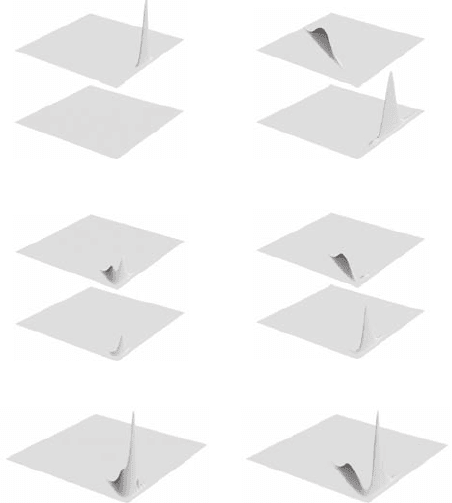
Bipolar Quantum Trajectory Methods 247

(a) t = 0 a.u. (d) t = 4500 a.u.

(b) t = 2000 a.u. (c) t = 2750 a.u.

(e) t = 2000 a.u. (unipolar)

(f) t = 2750 a.u. (unipolar)

FIGURE 15.6 Bipolar wavepacket dynamics for the collinear H + H

system. Each plot

represents a “snapshot” for a speciﬁc time, t, as listed. The initial wavepacket is right-incident.

The reaction coordinate extends over the right-front edge of the plots, turns the bottom corner,

and then heads back into the 3D plot frame. The top four plots, a–d, indicate bipolar component

wavepacket densities, chronologically, in counter-clockwise order. For comparison, the bottom

two plots, (e) and (f), represent the corresponding unipolar density, at the two intermediate

times. Interference nodes are markedly evident in the trailing (right) edge of plot (e), but do

not occur in the corresponding bipolar plot (b). (Reprinted with permission from Poirier, B.,

Journal of Chemical Physics, 129, 084103, 2008.)

independent (noncommunicating) trajectory ensembles, along the lines of CTS and

TSH. While the latter is more readily applicable to extremely large molecular sys-

tems (hundreds to thousands of dimensions), the former constitutes an exact quantum

dynamics method that defeats exponential scaling with system dimensionality [25].

Both methods are radical departures from the current state-of-the-art that may greatly

extend the applicability of accurate quantum dynamics calculations.

Regarding (1), synthetic bipolar QTM calculations have been performed [27,28],

for which two chief difﬁculties were encountered: (a) ψ

−

is initially zero; (b) in the

classical limit, bipolar quantum trajectories can get extremely close to one another,

essentially because they are “trying” to cross through a caustic. Successful remedies

have been found to resolve these issues [27,28], leading to the ﬁrst-ever successful

248 Quantum Trajectories

exact (worst relative error ∼ 10

−4

) synthetic QTM wavepacket calculation for a

system with substantial reﬂection interference.

Regarding (2), various independent-trajectory approaches have been explored,

including bipolar Path Integral Monte Carlo [29], quantum bipolar TSH [29], classical

bipolar TSH [30], and the bipolar derivative propagation method (DPM) [31], with the

last two the most successful to date. Bipolar DPM has been successfully applied to an

extremely challenging model system, involving an Eckart barrier reaction coordinate,

strongly coupled to up to 300 perpendicular bath modes. Accurate transmission and

reﬂection probabilities were achieved across the entire energetic range [31]. Classical

bipolar TSH is another very promising approach, in which the classical limit of large

mass—but not necessarily large energy—is presumed (the distinction is important,

because there is no reﬂection as E →∞) [30]. As a consequence, classical bipolar

TSH can be applied at all E, and for single-PES systems, and with no forbidden

energy hop problem—a great advance beyond standard TSH [5,6]. Moreover, it seems

to perform quite well even for comparatively small masses. On the other hand, the

results depend somewhat on the choice of V

eff

(x), which is analogous to the choice

of electronic states in standard TSH (e.g., diabatic vs. adiabatic).

15.8 CONCLUSIONS

In general, the study of QTMs is conducted for three reasons. The ﬁrst is foundational:

quantum trajectories provide insight into the nature of quantum mechanics itself, and

particularly, classical correspondence. The second is analytical: for a given molecu-

lar system, quantum trajectories provide classical-like insight into the dynamics and

physics of the relevant processes. The third is synthetic: QTMs comprise an efﬁcient

means of actually solving the TDSE for quantum dynamical systems. The bipolar

approach offers advantages in all three areas. Foundationally, bipolar (or more gen-

erally, multipolar) QTMs provide true classical correspondence, even when there is

substantial interference—a contingency for which the standard pure Bohm unipo-

lar QTM is ill-equipped to succeed. Analytically, bipolar quantum trajectories offer

a more classical-like, physically correct description of processes involving interfer-

ence. Synthetically, bipolar QTMs greatly ameliorate—if not eradicate—the infamous

“node problem” plaguing unipolar treatments, thus enabling accurate, stable synthetic

QTM calculations to be performed for the ﬁrst time for systems with substantial

reﬂection interference. The bipolar approach also greatly extends the applicability,

and perhaps performance, of standard TSH methodologies.

Of course, there is still more work to be done in future. Better time integrators and

ﬁtting/spatial differentiation routines are needed, in order to simplify and streamline

the current synthetic bipolar QTM codes. Bipolar generalizations in broader con-

texts such as multisurface dynamics [23] and complex-valued QTMs [32] will be

further developed. However, the most important future development may well prove

to be theoretical—speciﬁcally, the derivation of a unique V

eff

(x) potential function for

scattering systems, as already exists for 1D stationary bound states, and discussed in

Section 15.3. This will likely enable advances in a variety of different bipolar contexts.

Bipolar Quantum Trajectory Methods 249

BIBLIOGRAPHY

1. D. Frenkel and B. Smit, Understanding Molecular Simulations (Academic, New York,

2002).

2. G. D. Billing, Classical Path Method in Inelastic and Reactive Scattering, Int. Rev. Phys.

Chem. 13, 309 (1994).

3. N. Fröman and P.O. Fröman, JWKB Approximation (North-Holland, Amsterdam, 1965).

4. W. H. Miller, The Semiclassical Initial Value Representation: A Potentially Practical

Way for Adding Quantum Effects to Classical Molecular Dynamics Simulations, J. Phys.

Chem. A, 105, 2942 (2001).

5. G. A. Voth, Path-Integral Centroid Methods in Quantum Statistical Mechanics and

Dynamics, in I. Prigogine (ed.), Advances in Chemical Physics (Wiley, New York, 1996),

pp. 135–218.

6. J. C. Tully, Molecular Dynamics with Electronic Transitions, J. Chem. Phys. 93, 1061

(1990).

7. J. C. Tully, Nonadiabatic Dynamics, in D. L. Thompson (ed.), Modern Methods for

Multidimensional Dynamics Computations in Chemistry (World Scientiﬁc, Singapore,

1998).

8. Beyond the Molecular Frontier: Challenges for Chemistry and Chemical Engineering.

OrganizingCommittee for the Workshop on Information and Communications, Committee

on Challenges for the Chemical Sciences in the 21

Century, National Research Council,

2003.

9. B. K. Day, A. Askar, and H. Rabitz, Multidimensional Wave Packet Dynamics Within

the Fluid Dynamical Formulation of the Schrödinger Equation, J. Chem. Phys. 109, 8770

(1998).

10. C. L. Lopreore and R. E. Wyatt, Quantum Wave Packet Dynamics with Trajectories, Phys.

Rev. Lett. 82, 5190 (1999).

11. E. R. Bittner, Quantum Tunneling Dynamics using Hydrodynamic Trajectories, J. Chem.

Phys. 112, 9703 (2000).

12. R. E. Wyatt, Quantum Dynamics with Trajectories: Introduction to Quantum Hydrody-

namics (Springer, New York, 2005).

13. D. Babyuk and R. E. Wyatt, Multidimensional Reactive Scattering with Quantum

Trajectories: Dynamics with 50–200 Vibrational Modes, J. Chem. Phys. 124, 214109

(2006).

14. V. E. Madelung, Quantentheorie in hydrodynamischer form, Z. Physik 40, 322 (1926)

15. D. Bohm, A Suggested Interpretation of the Quantum Theory in Terms of “Hidden” Vari-

ables. I, Phys. Rev. 85, 166 (1952).

16. D. Bohm, A Suggested Interpretation of the Quantum Theory in Terms of “Hidden” Vari-

ables. II, Phys. Rev. 85, 180 (1952).

17. P. R. Holland, The Quantum Theory of Motion (Cambridge University Press, Cambridge,

1993).

18. K. Berndl, M. Daumer, D. Dürr, S. Goldstein, and N. Zanghi, A Survey of Bohmian

Mechanics, Il Nuovo Cimento 110B, 735 (1995).

19. B. Poirier, Reconciling Semiclassical and Bohmian Mechanics: I. Stationary States,

J. Chem. Phys., 121, 4501–4515 (2004).

20. C.Trahanand B. Poirier, Reconciling Semiclassical and Bohmian Mechanics. II. Scattering

States for Discontinuous Potentials, J. Chem. Phys., 124, 034115 (2006).

21. C. Trahan and B. Poirier, Reconciling Semiclassical and Bohmian Mechanics. III. Scat-

tering States for Continuous Potentials, J. Chem. Phys., 124, 034116 (2006).

250 Quantum Trajectories

22. B. Poirier, Development and Numerical Analysis of “Black-box” Counter-propagating

Wave Algorithm for Exact Quantum Scattering Calculations, J. Theoret. Comput. Chem.,

6, 99–125 (2007).

23. B. Poirier and G. Parlant, Reconciling Semiclassical and Bohmian Mechanics. IV. Multi-

surface Dynamics, invited contribution, special issue to honor Bob Wyatt, J. Phys. Chem

A. 111, 10400–10408 (2007).

24. B. Poirier, Reconciling Semiclassical and Bohmian Mechanics. V. Wavepacket Dynamics,

J. Chem. Phys., 128, 164115 (2008).

25. B. Poirier, Reconciling Semiclassical and Bohmian Mechanics. VI. Multidimensional

Dynamics, J. Chem. Phys., 129, 084103 (2008).

26. D. Babyuk and R. E. Wyatt, Coping with the Node Problem in Quantum Hydrodynamics:

The Covering Function Method, J. Chem. Phys. 121, 9230 (2004).

27. K. Park, B. Poirier, and G. Parlant, Quantum Trajectory Calculations for Bipolar

Wavepacket Dynamics in One Dimension, J. Chem. Phys. 129, 194112 (2008).

28. K. Park and B. Poirier, Quantum Trajectory Calculations for Bipolar Wavepacket Dynam-

ics Calculations in One Dimension: Synthetic Single-Wavepacket Propagation, J. Theoret.

Comput. Chem. in press.

29. J. Maddox and B. Poirier, Bipolar Quantum Trajectory Simulations: Trajectory Surface

Hopping vs. Path Integral Monte Carlo, Multidimensional Quantum Mechanics with Tra-

jectories, ed. D. V. Shalashilin and M. P. de Miranda (CCP6, Daresbury Laboratory, 2009).

30. J. Maddox and B. Poirier, Bipolar Quantum Trajectory Simulations: Classical Bipolar

Trajectory Surface Hopping Method, J. Chem. Phys., in preparation.

31. J. Maddox and B. Poirier, The Bipolar Derivative Propagation Method for Calculating

Stationary States for High-dimensional Reactive Scattering Systems, Multidimensional

Quantum Mechanics with Trajectories, ed. D. V. Shalashilin and M. P. de Miranda (CCP6,

Daresbury Laboratory, 2009).

32. T. Djama and B. Poirier, Analytical Solution of the Bipolar Decomposition for the Eckart

Barrier System: Ramiﬁcations for Complex-Valued Quantum Trajectories, J. Theoret.

Comput. Chem., in preparation.

33. A. S. Sanz, F. Borondo, and S. Miret-Artés, Causal Trajectories Description of Atom

Diffraction by Surfaces, Phys. Rev. B 61, 7743–7751 (2000).

Nondifferentiable

Bohmian Trajectories

Gebhard Grübl and Markus Penz

CONTENTS

16.1 Introduction.................................................................................................251

16.2 Bohmian Evolution for ψ ∈ C

..................................................................252

16.3 Bohmian Evolution for Ψ

∈ C

∞

...............................................................254

16.4 Bohmian Evolution for Ψ

∈ L

\ C

∞

.......................................................255

16.5 Hall’s Counterexample................................................................................257

Bibliography ..........................................................................................................261

16.1 INTRODUCTION

Quantum mechanics is often praised as a theory which uniﬁes classical mechanics

and classical wave theory. Quanta are said to behave either as particles or waves,

depending on the type of experiment they are subjected to. But where in the stan-

dard formalism can a pointlike particle structure actually be found? Perhaps only to

some degree in the reduction postulate applied to position measurements. In reac-

tion to this unsatisfactory state of affairs, Bohmian mechanics introduces a mathe-

matically precise particle concept into quantum mechanical theory. The fuzzy wave

functions are supplemented by sharp particle world-lines. Through this additional

structure some quantum phenomena like the double slit experiment have lost their

mystery.

Clearly the additional structure of particle world-lines brings along its own math-

ematical problems. Ordinary differential equations are generated from solutions of

partial differential equations. A mathematically convincing general treatment so far

has been given for a certain type of wave functions which do not exhaust all possi-

ble quantum mechanical situations. Exactly this fact has led some workers to doubt

that a Bohmian mechanics exists for all initial states Ψ

of a Schrödinger evolu-

tion t → e

−iht

. We shall show for one speciﬁc case of a counterexample Ψ

how the problem might be resolved in general. We approximate the state Ψ

, for

which the Bohmian velocity ﬁeld does not exist, by states which do have one. Their

integral curves turn out to converge to limit curves which can be taken to con-

stitute the Bohmian mechanics of the state unamenable to Bohmian mechanics at

ﬁrst sight.

251

252 Quantum Trajectories

16.2 BOHMIAN EVOLUTION FOR ψ ∈ C

Let ψ : R × R

→ C be twice continuously differentiable, i.e., ψ ∈ C

(

R × R

)

and let ψ obey Schrödinger’s partial differential equation

i∂

(

t, x

)

=−



∆ψ

(

t, x

)

+ V

(

)

(

t, x

)

(16.1)

with V : R

→ R being smooth, i.e., V ∈ C

∞

(

)

. From ψ, which is called a

classical solution of Schrödinger’s equation, a deterministic time evolution x →

(

)

of certain points x ∈ R

can be derived: If there exists a unique maximal

solution γ

: I

→ R

to the implicit ﬁrst order system of ordinary differential

equations

(

t, γ

(

))

(

)

= j

(

t, γ

(

))

(16.2)

with the initial condition γ

(

)

= x, one takes γ

as the evolution of x. Here ρ

R × R

→ R and j

: R × R

→ R

with

(

t, x

)

(

t, x

)

and j

(

t, x

)







(

t, x

)

∇

(

t, x

)



(16.3)

obey the continuity equation ∂

(

t, x

)

=−divj

(

t, x

)

for all

(

t, x

)

∈ R×R

. From

now on we shall drop the index ψ from ρ

and j

For certain solutions

∗

ψ the curves γ

can be shown to exist on a maximal domain

= R for all x ∈ R

: If ψ has no zeros, then the velocity ﬁeld v = j/ρ is a

-vector ﬁeld. v then obeys a local Lipschitz condition such that the maximal solu-

tions are unique. If in addition there exist continuous nonnegative real functions α, β

with

(

t, x

)

≤ α

(

)

+ β

(

)

then all maximal solutions of Equation 16.2 are

deﬁned on R and the general solution

Φ :

x∈R

{

}

→ R

with Φ

(

t, x

)

= γ

(

)

extends to all of R × R

(Thm 2.5.6, Ref. [1]). Due to the uniqueness of maximal

solutions the map Φ

(

t, ·

)

: R

→ R

is a bijection for all t ∈ R. It obeys

†



(

t,Ω

)

(

t, x

)

x =



Ω

(

0, x

)

x (16.4)

for all t ∈ R and for all open subsets Ω ⊂ R

with sufﬁciently smooth boundary such

that the integral theorem of Gauss can be applied to the space-time vector ﬁeld

(

ρ, j

)

on the domain



∈

(

0,t

)





, Ω



[2].

These undisputed mathematical facts have instigated Bohm’s amendment of Equa-

tion 16.1 in order to explain the fact that macroscopic bodies usually are localized

much more strictly than their wave functions suggest.

∗

The simplest explicitly solvable example is provided by the plane wave solution ψ

(

t, x

)

= e

−i

t+ik·x

Its Bohmian evolution Φ obeys Φ

(

t, x

)

= 2tk. Another explicitly solvable case is given by a Gaussian

free wave packet.

†

Here Φ

(

t, Ω

)

{

(

t, x

)

x ∈ Ω

}

Nondifferentiable Bohmian Trajectories 253

In Bohm’s completion of nonrelativistic quantum mechanics it is assumed that

any closed system has at any time, in addition to its wave function, a position in its

conﬁguration space and that this position evolves according to the general solution Φ

induced by the wave function. One says that the position is guided by ψ since Φ is

completely determined by ψ (and no other forces than the ones induced by ψ are

allowed to act on the position). More speciﬁcally, γ

is assumed to give the position

evolution for an isolated particle with wave function ψ

(

0, ·

)

and position x—both at

time t = 0.

As is common in standard quantum mechanics, ψ

(

0, ·

)

is supposed to obey



(

0, x

)

x = 1.

The nonnegative density ρ

(

0, ·

)

is interpreted as the probability density of the position

which the particle has at time t = 0. Since an initial position x is assumed to evolve

into γ

(

)

, the position probability density at time t is then, due to Equation 16.4,

given by ρ

(

t, ·

)

. In particular, Bohm’s completion gives the position probabilities,

among all the other spectral probability measures, a fundamental status, since the

empirical meaning of the other ones, as for instance momentum probabilities, are all

deduced from position probabilities.

There are classical solutions of Schrödinger’s equation, whose general solution Φ

does not extend to all of R × R

. An obstruction to do so can be posed by the zeros

of ψ. In the neighborhood of such a zero the velocity ﬁeld v = j /ρ may be unbounded

and v then lacks a continuous extension into the zero. As an example consider a time

0 wave function ψ

(

0, ·

)

: R

→ C, for which ψ

(

0, x, y

)

= x

+ iy

within a

neighborhood U of its zero

(

x, y

)

(

0, 0

)

. Within U (0, 0) for the velocity ﬁeld it

follows that



(

0, x, y

)

=

∂

(

0, x, y

)

(

0, x, y

)

=−

2xy

+ y

Hence for 0 <

< π/2 we have v

(

r cos φ, r sin φ

)

→−∞for r → 0 with φ

ﬁxed. Thus the implicit Bohmian evolution equation 16.2 is singular in a zero of the

wave function whenever the velocity ﬁeld does not have a continuous extension into it.

As a consequence the evolution γ

of such a zero x is not deﬁned by Equation 16.2.

As a related phenomenon there are solutions to Equation 16.2 which begin or end at

a ﬁnite time because they terminate at a zero of ψ.Anice example [3] for this to happen

is provided by the zeros of the harmonic oscillator wave function ψ : R

→ C with

(

t, x

)

= e

−



1 + e

−2it



1 − 2x



For example, the points

= 1 are zeros of ψ

(

t, ·

)

at the times t ∈ πZ. They are

singularities of v since

lim

t→0

t

∂

(

t, ±1

)

(

t, ±1

)

=±2.