Черненко В.Д. Высшая математика в примерах и задачах (том 1)
Подождите немного. Документ загружается.


100
Гпава 3
2°.
Площадь треугольника с вершинами Mj(jCj
^y^^M^Xj,y>^
и М^х^.у^ вычисляется по формуле
Если, следуя по контуру треугольника от Mj к М^ и к М^,
площадь обходится против часовой стрелки, то число S положи-
тельное, в противном случае — отрицательное. Поскольку пло-
щадь треугольника—величина положительная, то правая часть
формулы (3) берется по абсолютной величине.
Если площадь треугольника равна
нулю,
то из формулы (3)
следует равенство
которое является условием того, что три точки М^ , М^ ^ М^
расположены на одной прямой.
3°.
Площадь многоугольника с вершинами М^{х^,у^,
M^Xj,y^, ... ,MJ^x^y^) определяется по формуле
2
fh'
11^^
У1
Уг
+
^2
Хз
Уг
Уъ
+
..
..+
X.
X,
Уп
Л
Л
)\
(5)
4°.
Если
в
точках М^{х^,у^,
М2{х2,У^,
М-рс^,у^ помещены
массы
т^,т2,т^
соответственно, то координаты центра тяжести
этих масс находятся по формулам
_ mjXj +
1712X2
+ ^3X3
m,
+
m2
+
W3
^ЩУ1'^ЩУ2
+
^зУз
Ус
Wj +
W2
+
т^
(6)
Отсюда координаты центра тяжести площади однородного
треугольника определяются по формулам
X,+х,+x,
_У\^Уг'^Уъ
3
х^
-•
Ус=-
(7)
Координаты центра тяжести системы, состоящей из п ма-
териальных точек М^{х^,у^,М2{х2,У2), ... 5^п(^п'^л)' соответ-
ственно с массами
т^,т2,
,т^, определяются по формулам

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 101
m,x,+m,x,+...
+ m„x„
^ЩУх+ЩУ2+-
+ т„У„
^„^
^с ^ Ус ' (8)
2.1.
Найти точку, делящую отрезок между точками МД-1,8)
и М<.(3,3) в отношении ^ - ~.
^ 2
Решение. Для отыскания координат точки, делящей отре-
, 3
зек в отношении ^ ~
;>^,
воспользуемся формулами (1)
3 3
-1Ч---3 .
8
+ -.3
2 5 2 с
х-
у-
=
7'
^
=
—V
=
^-
1
+ - '
1
+ -
2 2
2.2.
Найти точку С, делящую отрезок между точками А{-2)
и 5(4) на оси в отношении
Я
==-2.
Решение. Считаем, что точки
AVLB
расположены на оси х,
тогда для отыскания точки
С
можно воспользоваться первой из
формул (1)
-1-2-4 ^^
х
=
= 10.
1-2
2.3.
В
треугольнике с вершинами
>4(-2,0),
В{в,6\
С(1
,-4) оп-
ределить длину медианы AD, длину биссектрисы АЕ, вычислить
площадь треугольника и координаты центра тяжести, полагая
его однородным.
Решение.
Так как медиана AD делит отрезок 5С пополам (рис.
3.4),
то
Я
=
1
и координаты точки D находятся по формулам (2)
6+1 7 6-4 ,
"" 2 2 "" 2
Отсюда длина медианы AD = ^(7 /
2
+ 2) +
(1
-
0)
= — v5 .
BHCCKTpHca^^" делит сторону БСна отрезки пропорциональ-
АВ BE
ные прилежащим сторонам, т. е.
АС ЕС
•
=
Я.

102 Гпава 3
Рис. 3.4
Найдем длины отрезков АВиАС
\AB\=yl(6
+
2f+6^
=10; МС
1=7(1
+ 2)'+ (-4)' =5-
Отсюда
Я
=2 и координаты точки Е
6+2_8 _6-2-4_ 2
1
+ 2~3' •^^~
1
+
2
~ 3'
Xg —
•
Длина биссектрисы АЕ
\АЕ\=.
8
+
2
t Г 2V
+ —
)
=f^-
Площадь треугольника находим по формуле (3), полагая
координаты точки Азз,х^,у^, точки В за
^2,
у2-,
С — за х^,у^
5 = -|[-2(6
+ 4)
+ 6(-4-0) +
1(0-6)]|
= 25кв.ед.
Координаты центра тяжести находим по формулам (7)
_-2 +
6 +
1_5^ _0 + 6-4_2
3 ~3' ^~ 3 ~3'
2.4.
Даны три последовательные вершины параллелограм-
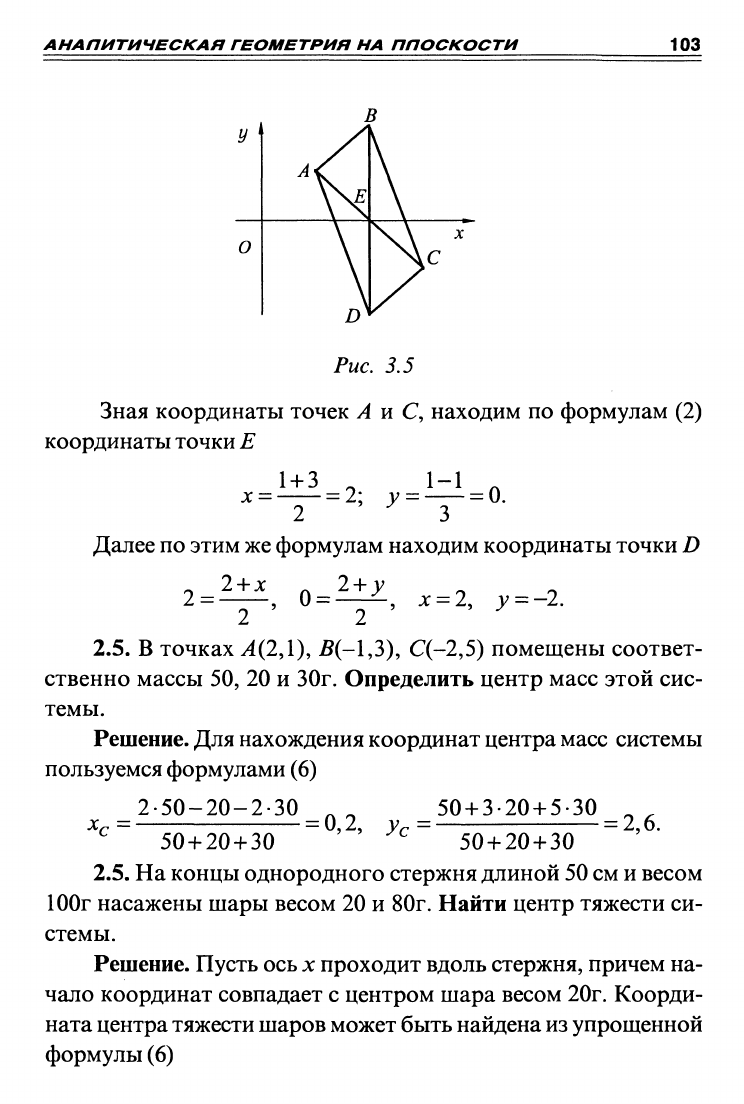
ма ^(1Д), В{2,2), С(3,-1). Найти четвертую вершину.
Решение. Диагонали параллелограмма
в
точке пересечения
jE"
делятся пополам (рис. 3.5).
АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
103
Рис. 3.5
Зная координаты точек А и С, находим по формулам (2)
координаты точки Е
1
+
3
. 1-1 ^
2 ^3
Далее по этим же формулам находим координаты точки D
2 +
х ^ 2+у
2=^-,
0 = ^, х
=
2, у
=
-2.
2.5.
В точках ^(2,1), 5(-1,3), С(-2,5) помещены соответ-
ственно массы 50, 20 и 30г. Определить центр масс этой сис-
темы.
Решение. Для нахождения координат центра масс системы
пользуемся формулами (6)
2.50-20-2-30
^,
50
+ 3-20
+
5-30 ^^
Хг = = 0,2,
Уг
= = 2,6.
"^
50
+ 20
+ 30
^
50
+ 20
+
30
2.5.
На концы однородного стержня длиной 50 см и весом
ЮОг насажены шары весом 20 и 80г. Найти центр тяжести си-
стемы.
Решение. Пусть ось х проходит вдоль стержня, причем на-
чало координат совпадает с центром шара весом 20г. Коорди-
ната центра тяжести шаров может быть найдена из упрощенной
формулы (6)

104
Гпава 3
т,х,+т^х. 200
+
80-50 ^^
=
—LJ
LJ. = = 40СМ.
т^
+т2
20 +
80
Координата центра тяжести стержня находится посередине
стержня на расстоянии
25
см от начала координат. Полагая, что
в этой точке Xj=25 см приложен вес стержня т^=100 г, а в точке
^2=40 см вес шаров, по этой же формуле находим центр тяжести
системы
100-25+ 100-40
х^
—
•
= 32,5см.
100
+ 100
2.7. Проверить, лежат ли точки Mj(2,l), М2(0,5), M^(-IJ)
на одной прямой.
Решение. Воспользуемся формулой (4)
2(5-7) + 0(7-1)-1(1-5) = -4
+
4 = 0.
Поскольку левая часть равенства тождественно равна нулю,
то точки лежат на одной прямой.
2.8. Вычислить площадь пятиугольника с вершинами
М,(2,3),
М^{-2,2),
Мз(-4-1),
М,(-1-5),
М,{4-2).
Решение. Запишем формулу
(5)
для пятиугольника
S =
fh'
^'
\[\х2
Уг
+
^2 У2
h Уг
+
Хъ Уу
^4 У^
+
^4 Ул\
^5 У$\
1^5
У5
Fl Ух
\
J
\(\1 3
-2 2
iv
+
-2 2
-Л -1
+
-4
-1
-1
-5
+
-1
4
-5|
-А
|4
V
-2h
3
'/1
И
подставим в нее координаты вершин
2
= -|(4+6) +
(2
+
8)
+ (20-1) +
(2
+
20)
+
(12
+
4)|
= 38,5кв.ед.
2.9. Найти координаты центра тяжести фермы
(рис.
3.6), со-
стоящей из однородных стержней.

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ППОСКОСТИ
105
У^
4
1
0
В
с
Е
1.5
\D
1.5
J
\А
^
X
Рис. 3.6
Решение. Поскольку стержни однородны, то масса т. каж-
дого стержня пропорциональна его длине
/.,
то есть т. = р1., где
р —линейная плотность.
Используя данные
рис.
3.6, найдем массу каждого стержня
и его центр тяжести.
Стд)жень
ОА
АВ
ВО
CD
EF
0D
Масса
т,=3р
т2=5р
Шз=4р
т^=\,5р
т^=\,5р
/«6=2,5 р
Центр
тяжести
М,(1,5;0)
M^iUS;!)
Мз(0;2)
Л//0,75;2)
^5(1,5;!)
М,(0,75;1)
Центр тяжести системы из шести материальных точек
Мр ..., М^ находим по формулам (8)
_ р(3-1,5 + 51,5 + 40+1,5-0,75 +
1,51,5
+
2,5-0,75
^^~
(3
+ 5+4+1,5 +
1,5+2,5)р
~ '
_р(3-0+5-2+4-2 + 1,5-2 + 1,5-1+2,5-1^
^^~ (3+5+4+1,5 +
1,5+2,5)р

106
Гпава 3
З.З.Уравнения прямой линии.
Геометрическое истолкование неравенства
и системы неравенств первой степени
Прямой линии на плоскости соответствует уравнение пер-
вой степени
с
двумя неизвестными.
1°.
Общее уравнение прямой
^x
+
5j + C = 0, (1)
здсь
А,в, с—произвольные коэффициенты.
V, Уравнение прямой
с
угловым коэффициентом
у^кх^-Ъ,
(2)
здесь к
=
tg(p — угловой коэффициент прямой, (р — угол на-
клона прямой к положительному направлению оси Ох, b — ве-
личина отрезка, отсекаемая прямой на оси Оу от начала
координат
(рис.
3.7).
Рис. 3J
Пользуясь уравнением прямой (2) можно установить, как
измнится это уравнение, если от данной прямой L перейти к пря-
мой
(рис.
3.8), ей симметричной.
При симметрии относительно оси Ох следует изменить знак
коэффициента при х и свободного члена или изменить знак ко-
эффициента при у. На
рис.
3.8. эта линия обозначена цифрой 1.
АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ППОСКОСТИ
107
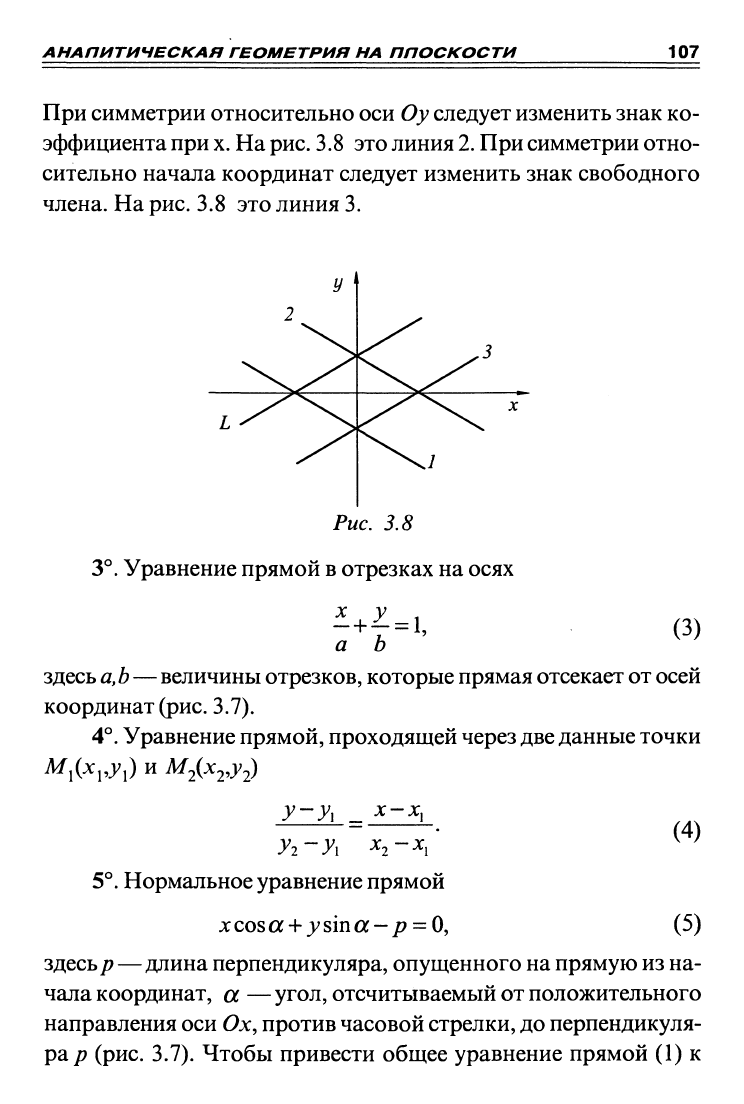
При симметрии относительно оси Оу следует изменить знак ко-
эффициента при
X.
На
рис.
3.8 это линия
2.
При симметрии отно-
сительно начала координат следует изменить знак свободного
члена. На рис. 3.8 это линия 3.
Рис. 3.8
3"".
Уравнение прямой в отрезках на осях
а b
(3)
здесь
а,Ь
—
величины отрезков, которые прямая отсекает от осей
координат
(рис.
3.7).
4°.
Уравнение прямой, проходящей через две данные точки
У-Ух
Уг-Ух
5°.
Нормальное уравнение прямой
xcosa + j;sina-/? = 0,
(4)
(5)
здесь/?—длина перпендикуляра, опущенного на прямую из на-
чала координат, а —
угол,
отсчитываемый от положительного
направления оси Ох, против часовой стрелки, до перпендикуля-
ра/? (рис. 3.7). Чтобы привести общее уравнение прямой (1) к

108
Гпава
3
нормальному
виду,
нужно общее уравнение прямой умножить на
нормирующий множитель
^= Г1—Т- (6)
взятый
со
знаком, противоположным знаку свободного члена С,
а если С =
О,
то знак может быть любой.
6°.
Геометрическое истолкование неравенства первой сте-
пени.
В
общем случае неравенство первой степени
Ах-^Ву+С^
О
определяет полуплоскость, которая при С
:^
устанавливается на
основании знака С. Если при х = Оиу = 0 знак С совпадает со
смыслом неравенства, то полуплоскость, соответствующая ему
включает начало координат; если же знак
С
противоречит нера-
венству, то соответствующая ему полуплоскость не включает
начала координат. Если С=
О,
то следует ориентироваться на
произвольно выбранную точку.
3.1.
Написать уравнение прямой проходящей через точку
Л(3,4) и составляющей с Ох угол 45°.
Воспользуемся уравнением прямой
с
угловым коэффициен-
том (2). Угловой коэффициент k=ig(p= tg45''=l. Подставляя в
уравнение (2) координаты точки А и значение
/с,
находим пара-
метр
Ь:
4 =
3+Ь,
откуда Ь=1 и уравнение примет вид
j;
= л:+1
или в общем виде
х-у+1
= 0.
3.2.
По уравнению прямой
j^
=-2JC+3
написать уравнения пря-
мых, симметричных относительно осей
и
начала координат. Сде-
лать чертеж.
Решение. Для случая симметрии относительно оси Ох бу-
дем иметь
уравнение}^
=
2х-3;
для случая симметрии относитель-
но оси Оу — уравнение у =
2х+3;
для случая симметрии
относительно начала координат — уравнение у =-2x-3.
На
рис.
3.9 эти линии, соответственно, обозначены цифра-
ми
1,2,3.
АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ППОСКОСТИ
109
Рис. 3.9
3.3.
Даны точки 0(0,0) и
^(4,0).
На отрезке О А построен па-
раллелограмм, диагонали которого пересекаются в точке
Б(0,3).
Написать уравнения сторон
и
диагоналей параллелограмма.
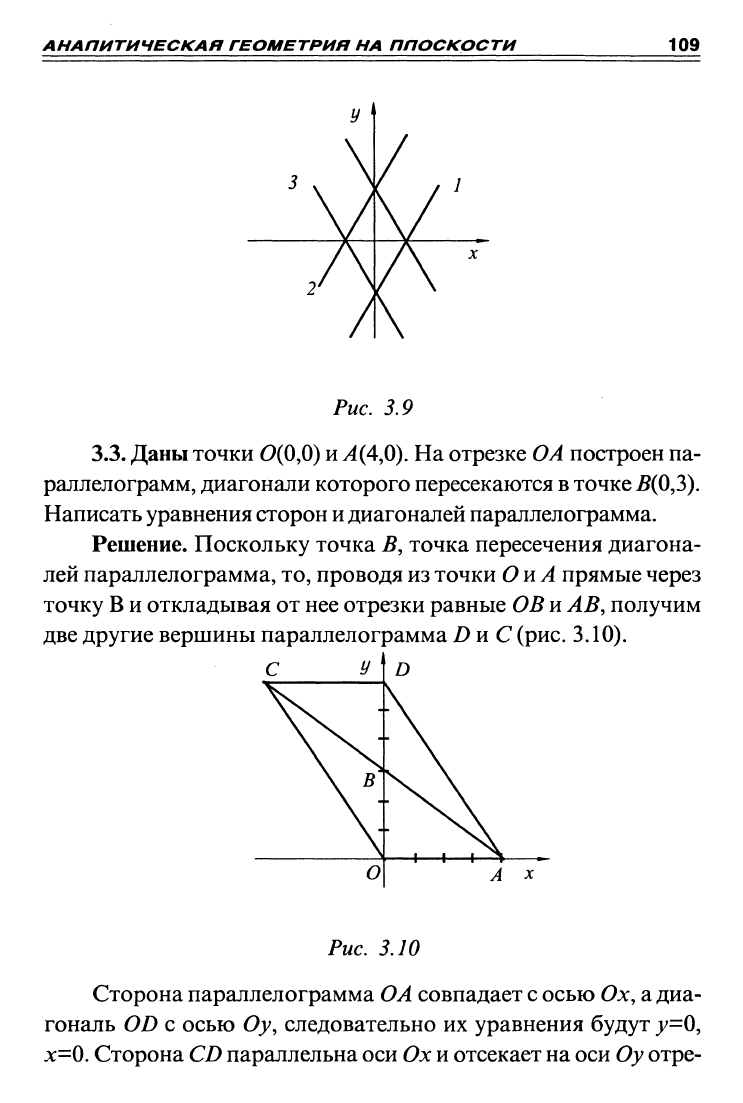
Решение. Поскольку точка В, точка пересечения диагона-
лей параллелограмма, то, проводя из точки ОиА прямые через
точку В и откладывая от нее отрезки равные ОВ и АВ, получим
две другие вершины параллелограмма
Z)
и С
(рис.
3.10).
С У
Рис. 3.10
Сторона параллелограмма О А совпадает с осью Ох, а диа-
гональ OD с осью Оу, следовательно их уравнения будут
y=Q,
х=0.
Сторона CD параллельна оси Ох и отсекает на оси Оу отре-
