Чулков П.В. Уравнения и неравенства в школьном курсе математики
Подождите немного. Документ загружается.

Ï.Â. ×ÓËÊÎÂ
Óðàâíåíèÿ è íåðàâåíñòâà
â øêîëüíîì êóðñå ìàòåìàòèêè
Ëåêöèè 14
Ìîñêâà
Ïåäàãîãè÷åñêèé óíèâåðñèòåò
«Ïåðâîå ñåíòÿáðÿ»
2006

Ëåêöèÿ 1
Îáùèå ñâåäåíèÿ îá óðàâíåíèÿõ,
íåðàâåíñòâàõ è èõ ñèñòåìàõ
Êðàòêîå ââåäåíèå
Ïðåäëàãàåìûé ìàòåðèàë èìååò, ïðåæäå âñåãî, ïðàêòè÷åñêóþ
íàïðàâëåííîñòü.
 ñâÿçè ñ ýòèì â òåêñòå ëåêöèé ñîäåðæèòñÿ áîëüøîå êîëè÷å-
ñòâî çàäà÷, íåêîòîðûå èç íèõ ñ ðåøåíèÿìè. Ïðåæäå ÷åì èçó-
÷àòü ýòè ðåøåíèÿ, æåëàòåëüíî ðåøèòü çàäà÷ó ñàìîñòîÿòåëüíî,
ñðàâíèòü ïîëó÷åííûé îòâåò, à çàòåì è ñàìî ðåøåíèå ñ ðåøåíèåì,
ïðèâåäåííûì â êîíöå ëåêöèè.
Ëåêöèÿ 1. Îáùèå ñâåäåíèÿ îá óðàâíåíèÿõ, íåðàâåíñòâàõ è èõ ñèñòå-
ìàõ. Ðàâíîñèëüíûå óðàâíåíèÿ è íåðàâåíñòâà. ÎÄÇ. Îáùèå ìåòîäû ðå-
øåíèÿ óðàâíåíèé. Àëãåáðàè÷åñêèå óðàâíåíèÿ. Ïðèìåðû
Ëåêöèÿ 2. Ìåòîäû ðåøåíèÿ íåðàâåíñòâ. ×èñëîâûå íåðàâåíñòâà è èõ
ñâîéñòâà. Äðîáíî-ðàöèîíàëüíûå íåðàâåíñòâà. Ìåòîä èíòåðâàëîâ è ñâîé-
ñòâà íåïðåðûâíîñòè
Ëåêöèÿ 3. Ìåòîäû ðåøåíèÿ ñèñòåì óðàâíåíèé. Àëãåáðàè÷åñêèå óðàâ-
íåíèÿ è èõ ñèñòåìû. Ìåòîä ïîäñòàíîâêè ïðè ðåøåíèè ñèñòåì óðàâíå-
íèé. Ñèììåòðè÷åñêèå è îäíîðîäíûå ñèñòåìû.
Êîíòðîëüíàÿ ðàáîòà ¹ 1
Ëåêöèÿ 4. Èððàöèîíàëüíûå óðàâíåíèÿ è íåðàâåíñòâà. Ìåòîäû ðåøå-
íèÿ èððàöèîíàëüíûõ óðàâíåíèé è íåðàâåíñòâ è èõ ñèñòåì. Óðàâíåíèÿ è
íåðàâåíñòâà ñ ìîäóëåì
Ëåêöèÿ 5. Òðèãîíîìåòðè÷åñêèå óðàâíåíèÿ è íåðàâåíñòâà. Ìåòîäû ðå-
øåíèÿ òðèãîíîìåòðè÷åñêèõ óðàâíåíèé è íåðàâåíñòâ è èõ ñèñòåì
Ëåêöèÿ 6. Ëîãàðèôìè÷åñêèå è ïîêàçàòåëüíûå óðàâíåíèÿ è íåðàâåíñòâà.
Ìåòîäû ðåøåíèÿ ëîãàðèôìè÷åñêèõ è ïîêàçàòåëüíûõ óðàâíåíèé è íåðà-
âåíñòâ è èõ ñèñòåì.
Êîíòðîëüíàÿ ðàáîòà ¹ 2
Ëåêöèÿ 7. Íåñòàíäàðòíûå ìåòîäû ðåøåíèÿ óðàâíåíèé è íåðàâåíñòâ.
Èñïîëüçîâàíèå ñâîéñòâ ôóíêöèé ïðè ðåøåíèè óðàâíåíèé è íåðàâåíñòâ.
Òðèãîíîìåòðè÷åñêèå ïîäñòàíîâêè. Âåêòîðû â àëãåáðå
Ëåêöèÿ 8. Óðàâíåíèÿ è íåðàâåíñòâà ñ ïàðàìåòðîì. Ïðèìåðû ðåøåíèÿ
óðàâíåíèé è íåðàâåíñòâ ñ ïàðàìåòðîì. Ãåîìåòðè÷åñêèå èíòåðïðåòàöèè.
Èòîãîâàÿ ðàáîòà
Ó÷åáíûé ïëàí êóðñà
¹ áð.
Íàçâàíèå ëåêöèè
1
1
1
1
2
2
2
2
Ïàâåë Âèêòîðîâè÷ ×óëêîâ
Ìàòåðèàëû êóðñà «Óðàâíåíèÿ è íåðàâåíñòâà â øêîëüíîì êóðñå ìàòåìàòèêè» :
Ëåêöèè 14. Ì. : Ïåäàãîãè÷åñêèé óíèâåðñèòåò «Ïåðâîå ñåíòÿáðÿ», 2006. 88 ñ.
Ó÷åáíî-ìåòîäè÷åñêîå ïîñîáèå
Ðåäàêòîð È.Ì. Áîêîâà
Êîððåêòîð Ë.À. Ãðîìîâà
Êîìïüþòåðíàÿ âåðñòêà Ä.Â. Êàðäàíîâñêàÿ
Ïîäïèñàíî â ïå÷àòü 20.06.2006.
Ôîðìàò 60×90
1
/
16
. Ãàðíèòóðà «SchoolBook». Ïå÷àòü îôñåòíàÿ. Ïå÷. ë. 5,75
Òèðàæ ýêç. Çàêàç ¹
Ïåäàãîãè÷åñêèé óíèâåðñèòåò «Ïåðâîå ñåíòÿáðÿ»,
óë. Êèåâñêàÿ, ä. 24, Ìîñêâà, 121165
http://edu.1september.ru
Ï.Â. ×óëêîâ, 2006
Ïåäàãîãè÷åñêèé óíèâåðñèòåò «Ïåðâîå ñåíòÿáðÿ», 2006

4
5
Îáùèå ñâåäåíèÿ îá óðàâíåíèÿõ, íåðàâåíñòâàõ è èõ ñèñòåìàõ
Ëåêöèÿ 1
Ïîñëåäîâàòåëüíîñòü èçëîæåíèÿ ìàòåðèàëà íåñêîëüêî îòëè÷íà îò
øêîëüíîé, ïîñêîëüêó ëåêöèè ðàññ÷èòàíû íà ó÷èòåëåé óæå íåîäíî-
êðàòíî «ïðîõîäèâøèõ» øêîëüíûé êóðñ ìàòåìàòèêè. Óêàçàííîå îá-
ñòîÿòåëüñòâî ïîçâîëÿåò ñ÷èòàòü íåêîòîðûå òåîðåòè÷åñêèå ñâåäåíèÿ
õîðîøî èçâåñòíûìè.
Íàïðèìåð, ðàññìàòðèâàÿ â ïåðâîé ëåêöèè óðàâíåíèÿ, ìû áó-
äåì ïî÷òè áåç âñÿêèõ îãîâîðîê ïðåîáðàçîâûâàòü èõ â òàê íàçûâà-
åìûå ñìåøàííûå ñèñòåìû, íåñìîòðÿ íà òî, ÷òî ñîáñòâåííî ñèñòå-
ìû óðàâíåíèé è íåðàâåíñòâ áóäóò ðàññìîòðåíû ïîçäíåå.
Îñíîâíûå îïðåäåëåíèÿ
Îïðåäåëèì óðàâíåíèå ñ îäíîé ïåðåìåííîé êàê ðàâåíñòâî âèäà
)
(
)
(
xgxf
=
, ãäå
)
(
xf
,
)
(
xg
íåêîòîðûå ôóíêöèè.
Ïðè ýòîì:
(1.1.)
1
Ðåøåíèåì (ëó÷øå êîðíåì) óðàâíåíèÿ íàçûâàþò òî
çíà÷åíèå ïåðåìåííîé, ïðè êîòîðîì äàííîå óðàâíåíèå îáðàùàåòñÿ
â âåðíîå ðàâåíñòâî.
(1.2.) Ðåøèòü óðàâíåíèå çíà÷èò íàéòè âñå êîðíè óðàâíåíèÿ
èëè äîêàçàòü, ÷òî óðàâíåíèå íå èìååò êîðíåé.
(1.3.) Îáëàñòüþ äîïóñòèìûõ çíà÷åíèé óðàâíåíèÿ (ïðèíÿòîå
ñîêðàùåíèå ÎÄÇ) íàçûâàþò ÷èñëîâîå ìíîæåñòâî, íà êîòîðîì
îïðåäåëåíû îáå ôóíêöèè
)
(
xf
è
)
(
xg
.
Ïîíÿòèå íåðàâåíñòâà è ñîïóòñòâóþùèå åìó ïîíÿòèÿ (ðåøåíèå
íåðàâåíñòâà, ðàâíîñèëüíûå íåðàâåíñòâà è ò.ä.) îïðåäåëÿþòñÿ
àíàëîãè÷íî.
Ýòè ïîíÿòèÿ ìû ïîäðîáíåå ðàññìîòðèì âî âòîðîé ëåêöèè, îä-
íàêî ïîëüçîâàòüñÿ íåêîòîðûìè èç íèõ áóäåì óæå â ïåðâîé.
Ïðèìåð 1. Íàéäèòå ÎÄÇ óðàâíåíèÿ
3
1
2
−
=−
x
x
Ðåøåíèå. Ôóíêöèÿ
2
)
(
−=
xxf
îïðåäåëåíà ïðè
2≥
x
, ôóíê-
öèÿ
3
1
)
(
−
=
x
xg
ïðè
3≠
x
.
Îòâåò:
[
2; 3
)(
3;
)
∪+∞.
Òàêæå ïðèíÿòî ñ÷èòàòü, ÷òî:
(1.4.) Äâà óðàâíåíèÿ ðàâíîñèëüíû íà ìíîæåñòâå, åñëè îíè èìåþò
îäíè è òå æå êîðíè, ïðèíàäëåæàùèå äàííîìó ìíîæåñòâó. Ñëåäî-
âàòåëüíî, åñëè óðàâíåíèÿ íå èìåþò êîðíåé íà äàííîì ìíîæåñòâå,
òî îíè ðàâíîñèëüíû íà íåì.
Ïåðåõîä ê ðàâíîñèëüíîìó óðàâíåíèþ ïðèíÿòî îáîçíà÷àòü
çíàêîì «⇔».
(1.5.) Äàííîå óðàâíåíèå ÿâëÿåòñÿ ñëåäñòâèåì íåêîòîðîãî äðó-
ãîãî óðàâíåíèÿ, åñëè êàæäûé êîðåíü äðóãîãî óðàâíåíèÿ ÿâëÿåòñÿ
êîðíåì äàííîãî. Åñëè óðàâíåíèå íå èìååò êîðíåé, òî èç íåãî ñëå-
äóåò ëþáîå äðóãîå óðàâíåíèå.
Ïåðåõîä ê óðàâíåíèþ-ñëåäñòâèþ ïðèíÿòî îáîçíà÷àòü çíàêîì«⇒».
Ïðèìåð 2. Âåðíî ëè, ÷òî óðàâíåíèå
8
2
=
x
ðàâíîñèëüíî óðàâ-
íåíèþ
2105 =
x
íà ìíîæåñòâå à) äåéñòâèòåëüíûõ; á) ðàöèîíàëü-
íûõ ÷èñåë?
Ðåøåíèå. à) Íà ìíîæåñòâå äåéñòâèòåëüíûõ ÷èñåë ïåðâîå óðàâíå-
íèå èìååò êîðíè
22±
, à âòîðîå óðàâíåíèå èìååò åäèíñòâåííûé
êîðåíü
22
. Óðàâíåíèÿ íå ðàâíîñèëüíû.
á) Èç ïðåäûäóùåãî ñëåäóåò, ÷òî íà ìíîæåñòâå ðàöèîíàëüíûõ
÷èñåë îáà óðàâíåíèÿ êîðíåé íå èìåþò. Óðàâíåíèÿ ðàâíîñèëüíû.
Îòâåò: à) íåò; á) äà.
Ïðèìåð 3. Âåðíî ëè, ÷òî óðàâíåíèå
2
5
xx
=
ÿâëÿåòñÿ ñëåäñòâè-
åì óðàâíåíèÿ
102 =
x
íà ìíîæåñòâå äåéñòâèòåëüíûõ ÷èñåë?
Ðåøåíèå. Óðàâíåíèå
102 =
x
èìååò åäèíñòâåííûé êîðåíü 5,
êîòîðûé òàêæå ÿâëÿåòñÿ êîðíåì óðàâíåíèÿ
2
5
xx
=
.
Ñëåäîâàòåëüíî,
102 =x
⇒
2
5
xx
=
.
Îòâåò: äà.
Êàê ìû ðåøàåì óðàâíåíèÿ? Ïðèìåðíî òàê: ïðîâîäèì íåêîòî-
ðûå ïðåîáðàçîâàíèÿ èñõîäíîãî óðàâíåíèÿ è ïîñòåïåííî ïðèõîäèì
ê íåêîòîðîìó óðàâíåíèþ, êîðíè êîòîðîãî óìååì íàõîäèòü. Êîðíè
ïîñëåäíåãî óðàâíåíèÿ è çàïèñûâàåì â îòâåò.
Íî ìîæíî ëè áûëî òàê ïîñòóïàòü? Äðóãèìè ñëîâàìè, ìîæåì
ëè ìû áûòü óâåðåíû â òîì, ÷òî êîðíè ïîñëåäíåãî óðàâíåíèÿ ÿâëÿ-
þòñÿ êîðíÿìè èñõîäíîãî óðàâíåíèÿ? Òî åñòü ñîâïàäàþò ëè ìíî-
æåñòâà êîðíåé ïðåîáðàçîâàííîãî è èñõîäíîãî óðàâíåíèé? Êàê ìû
1
Òàê ìû áóäåì íóìåðîâàòü îïðåäåëåíèÿ. (1.1.) îçíà÷àåò ïåðâîå îïðåäåëå-
íèå èç ïåðâîé ëåêöèè.

6
7
Îáùèå ñâåäåíèÿ îá óðàâíåíèÿõ, íåðàâåíñòâàõ è èõ ñèñòåìàõ
Ëåêöèÿ 1
óâèäèì â äàëüíåéøåì, ýòî íå âñåãäà òàê, äàæå åñëè ïðîâåäåííûå
ïðåîáðàçîâàíèÿ íå ñîäåðæàò âû÷èñëèòåëüíûõ îøèáîê. Íàïðèìåð,
ïðè ïðèâåäåíèè ïîäîáíûõ ñëàãàåìûõ, ïðè äåëåíèè îáåèõ ÷àñòåé
óðàâíåíèÿ íà íåêîòîðîå âûðàæåíèå, ñîäåðæàùåå ïåðåìåííóþ,
êîðíè ìîãóò áûòü «ïîòåðÿíû», à ïðè âîçâåäåíèè îáåèõ ÷àñòåé
óðàâíåíèÿ â êâàäðàò, íàîáîðîò, ìîãóò ïîÿâèòüñÿ òàê íàçûâàåìûå
«ïîñòîðîííèå êîðíè». Òî åñòü ðåøåíèå óðàâíåíèé ïðåäïîëàãàåò
íå òîëüêî ïîñëå íåêîòîðûõ (âîçìîæíî, íåïðîñòûõ) ïðåîáðàçîâà-
íèé ïîëó÷èòü ñòàíäàðòíîå óðàâíåíèå è «íàéòè õ», íî òàêæå äîêà-
çàòü, ÷òî ðåøåíî èìåííî èñõîäíîå óðàâíåíèå èëè íåðàâåíñòâî, à
íå òî ñòàíäàðòíîå óðàâíåíèå, êîòîðîå ìû ïîëó÷èëè â ðåçóëüòàòå
ïðåîáðàçîâàíèé.
Ïîýòîìó, ÷òîáû äîêàçàòü, ÷òî íàéäåíû âñå êîðíè èñõîäíîãî
óðàâíåíèÿ, íåîáõîäèìî ëèáî ñëåäèòü, ÷òîáû ïðè êàæäîì èç ïðî-
âîäèìûõ ïðåîáðàçîâàíèé â ðåçóëüòàòå ïîëó÷àëèñü óðàâíåíèÿ
(èëè ñìåøàííûå ñèñòåìû) ðàâíîñèëüíûå èñõîäíîìó óðàâíåíèþ,
ëèáî, ïîëó÷èâ öåïî÷êó ñëåäñòâèé èç èñõîäíîãî óðàâíåíèÿ, çàòåì
ñäåëàòü ïðîâåðêó, ïîäñòàâëÿÿ ïîëó÷åííûå êîðíè â èñõîäíîå óðàâ-
íåíèå.
Ïåðå÷èñëèì îñíîâíûå ñâîéñòâà ðàâíîñèëüíîñòè óðàâíåíèé.
Òåîðåìà 1. Åñëè ê îáåèì ÷àñòÿì óðàâíåíèÿ ïðèáàâèòü îäíî è
òî æå âûðàæåíèå, îïðåäåëåííîå íà ÎÄÇ èñõîäíîãî óðàâíåíèÿ, òî
ïîëó÷èì óðàâíåíèå ðàâíîñèëüíîå äàííîìó óðàâíåíèþ.
Èëè â âèäå ñõåìû:
ÎÄÇ.
()+ ()= ()+ (),
()= ()
fx px gx px
fx gx
x
⇔
∈
 ÷àñòíîñòè, åñëè ïåðåíåñòè ñëàãàåìîå èç îäíîé ÷àñòè â äðó-
ãóþ, òî ïîëó÷èì óðàâíåíèå, ðàâíîñèëüíîå èñõîäíîìó óðàâíåíèþ.
Òðåáîâàíèå
ÎÄÇx ∈ â ôîðìóëèðîâêå òåîðåìû ñóùåñòâåííî. Åñëè
ôóíêöèÿ
)
(
xp
îïðåäåëåíà íå äëÿ âñåõ x èç ÎÄÇ, òî ðàâíîñèëü-
íîñòü, âîáùå ãîâîðÿ, íàðóøàåòñÿ, è ïðåîáðàçîâàíèå ìîæåò ïðèâå-
ñòè ê ïîòåðå êîðíåé.
Íàïðèìåð, óðàâíåíèÿ
1=
x
è
1
1
1
1
1
−
+=
−
+
xx
x
íå ðàâíî-
ñèëüíû, ïîñêîëüêó âòîðîå óðàâíåíèå êîðíåé íå èìååò, òàê êàê
ôóíêöèÿ
1
1
)
(
−
=
x
xp
íå îïðåäåëåíà ïðè
1=
x
.
Òåîðåìà 2. Åñëè îáå ÷àñòè äàííîãî óðàâíåíèÿ óìíîæèòü íà îäíî
è òî æå íå ðàâíîå íóëþ âûðàæåíèå, îïðåäåëåííîå íà ÎÄÇ èñõîäíî-
ãî óðàâíåíèÿ, òî ïîëó÷èì óðàâíåíèå ðàâíîñèëüíîå äàííîìó.
Èëè â âèäå ñõåìû:
{
,
,
ÎÄÇ.
() ()
() () () ()
() 0
fx gx
fx px gx px
px
x
=
⋅=⋅
⇔
≠
∈
 ÷àñòíîñòè, åñëè ïîìåíÿòü çíàêè â îáåèõ ÷àñòÿõ óðàâíåíèÿ
(òî åñòü óìíîæèòü îáå ÷àñòè óðàâíåíèÿ íà
1
)
(
−=
xp
)
, òî ïîëó÷èò-
ñÿ óðàâíåíèå, ðàâíîñèëüíîå èñõîäíîìó óðàâíåíèþ.
Òðåáîâàíèÿ
ÎÄÇx ∈
è
0
)
(
≠
xp
â ôîðìóëèðîâêå òåîðåìû ñóùå-
ñòâåííû.  ÷àñòíîñòè, åñëè
0
)
(
=
xp
ïðè íåêîòîðîì
ÎÄÇx ∈
, òî
ïðåîáðàçîâàíèå ìîæåò ïðèâåñòè ê ïîÿâëåíèþ ïîñòîðîííèõ êîðíåé.
(Ñîîòâåòñòâóþùèé ïðèìåð ïðèäóìàéòå ñàìîñòîÿòåëüíî.)
Òåîðåìà 3. Åñëè îáå ÷àñòè äàííîãî óðàâíåíèÿ ðàçäåëèòü íà
îäíî è òî æå íå ðàâíîå íóëþ âûðàæåíèå, îïðåäåëåííîå íà ÎÄÇ
èñõîäíîãî óðàâíåíèÿ, òî ïîëó÷èì óðàâíåíèå, ðàâíîñèëüíîå äàí-
íîìó.
Èëè â âèäå ñõåìû:
,
ÎÄÇ.
() ()
() ()
() ()
()
0,
fx gx
fx gx
px px
px x
=
=⇔
≠∈
Êàê è â ïðåäûäóùèõ ñëó÷àÿõ, íàðóøåíèå òðåáîâàíèé
ÎÄÇx ∈
è
0
)
(
≠
xp
ìîæåò ïðèâåñòè ê íåðàâíîñèëüíûì ïðåîáðàçîâàíèÿì.
Äîêàçàòåëüñòâà òåîðåì 13 ñëåäóþò èç î÷åâèäíûõ ñâîéñòâ ÷èñ-
ëîâûõ ðàâåíñòâ. (Ïðîâåäèòå èõ ñàìîñòîÿòåëüíî.)
Íåñêîëüêî ñëîâ îá ÎÄÇ
Ìû âèäåëè, ÷òî ÎÄÇ ìîæåò áûòü ïîëåçíî ïðè îáîñíîâàíèè ðàâ-
íîñèëüíûõ ïåðåõîäîâ, íî îáÿçàòåëüíî ëè ïðè ðåøåíèè óðàâíåíèé
è íåðàâåíñòâ íàõîäèòü ÎÄÇ?
Èíîãäà ðåêîìåíäóþò ðåøàòü óðàâíåíèÿ (íåðàâåíñòâà, ñèñòåìû
óðàâíåíèé è íåðàâåíñòâ) ïî ñëåäóþùåé ñõåìå:
1) Íàéòè ÎÄÇ, òî åñòü ðåøèòü ñîîòâåòñòâóþùèå íåðàâåíñòâà è
âûïèñàòü â ÿâíîì âèäå, íà êàêîì ÷èñëîâîì ìíîæåñòâå èìååò ñìûñë
äàííîå óðàâíåíèå.
2) Ðåøèòü óðàâíåíèå ñ ïîìîùüþ òåõ èëè èíûõ ïðåîáðàçîâàíèé.

8
9
Îáùèå ñâåäåíèÿ îá óðàâíåíèÿõ, íåðàâåíñòâàõ è èõ ñèñòåìàõ
Ëåêöèÿ 1
3) Ïðîâåðèòü, ïðèíàäëåæàò ëè êîðíè äàííîãî óðàâíåíèÿ ÎÄÇ.
Ïîïðîáóåì îòâåòèòü íà ýòîò âîïðîñ, ðàññìîòðåâ íåñêîëüêî
ïðèìåðîâ. Ìîæåò ëè òàêîé ñïîñîá ðåøåíèÿ ïðèâåñòè ê ïîòåðå
êîðíåé èëè ïîÿâëåíèþ ïîñòîðîííèõ êîðíåé?
Ïðèìåð 4. Ðåøèòå óðàâíåíèå
11
25
+=++−
xxx
.
Ðåøåíèå. ÎÄÇ îïðåäåëÿåòñÿ èç óñëîâèÿ:
−−≤
52
10
xx
. Òàêîå íå-
ðàâåíñòâî ìîæíî ðåøèòü òîëüêî ïðèáëèæåííî. Íî åãî è íå íóæíî
ðåøàòü. Ìîæíî ïîñòóïèòü èíà÷å:
11
25
+=++−
xxx
⇔
⇔
≥+
+=++−
01
,
)
1
(
1
225
x
xxx
⇔
−≥
=+
1
,02
5
x
xx
⇔
−≥
=+
.1
,0
)
2
(
4
x
xx
Îòâåò: 0.
Êîììåíòàðèé. Âîçìîæíîñòü ïåðâîãî ðàâíîñèëüíîãî ïåðåõî-
äà ñëåäóåò èç îïðåäåëåíèÿ àðèôìåòè÷åñêîãî êâàäðàòíîãî êîð-
íÿ. Òàêîãî ðîäà ðàâíîñèëüíîñòè ðàññìîòðèì ïîäðîáíåå â ëåê-
öèè 4.
Ïðèìåð 5. Ðåøèòå óðàâíåíèå
xx
−=−12
.
Ðåøåíèå. ÎÄÇ ïîëó÷èì èç óñëîâèÿ
012 ≥−
x
. Òî åñòü
2
1
≥
x
.
Âîçâåäåì îáå ÷àñòè óðàâíåíèÿ â êâàäðàò:
2
12
xx
=−
,
012
2
=+−
xx
,
1=
x
. Ïîëó÷åííûé êîðåíü âõîäèò â ÎÄÇ, íî, êàê ëåãêî ïðîâåðèòü, íå
ÿâëÿåòñÿ êîðíåì äàííîãî óðàâíåíèÿ.
Îòâåò: íåò êîðíåé.
Çíà÷èò ëè ýòî, ÷òî íàõîæäåíèå ÎÄÇ â ïðèìåðå 5 ñîâñåì áåñïî-
ëåçíî? Íåò. Íåñêîëüêî èçìåíèì ðàññóæäåíèÿ: ïîñêîëüêó 2x1 ≥0,
òî
0
2
1
<−≤−
x
, ñëåäîâàòåëüíî,
210
x
−<
, ÷òî ïðîòèâîðå÷èò îï-
ðåäåëåíèþ àðèôìåòè÷åñêîãî êâàäðàòíîãî êîðíÿ.
Ïðèìåð 6. Ðåøèòå óðàâíåíèå
)
2lg
(
33
4
−+−=−
xxx
.
Ðåøåíèå. ÎÄÇ äàííîãî óðàâíåíèÿ îïðåäåëÿåòñÿ óñëîâèÿìè
3≥
x
è
x
≥3
, îòêóäà ñëåäóåò, ÷òî åäèíñòâåííîå çíà÷åíèå, óäîâëåòâîðÿ-
þùåå ÎÄÇ,
3=
x
.
Ïðîâåðêà ïîêàçûâàåò, ÷òî õ = 3 êîðåíü óðàâíåíèÿ.
Îòâåò: 3.
Âûâîäû:
1) Èíîãäà íàéòè ÎÄÇ òðóäíåå, ÷åì ðåøèòü óðàâíåíèå, à ìîæåò
áûòü, è âîâñå íåâîçìîæíî (ñì. ïðèìåð 4).
2) Òî, ÷òî íàéäåííûå êîðíè âõîäÿò â ÎÄÇ, âîâñå íå ãàðàíòèðó-
åò, ÷òî îíè óäîâëåòâîðÿþò èñõîäíîìó óðàâíåíèþ, äàæå åñëè âñå
ïðåîáðàçîâàíèÿ âûïîëíåíû áåç îøèáîê (ïðèìåð 5).
3) Èíîãäà èñïîëüçîâàíèå ÎÄÇ ïîëåçíî, ïîñêîëüêó äàåò âîçìîæ-
íîñòü áûñòðî ðåøèòü óðàâíåíèå (ïðèìåð 6).
Ïîëó÷àåòñÿ, ÷òî ÷àùå âñåãî íàõîäèòü â ÿâíîì âèäå ÎÄÇ íå îáÿ-
çàòåëüíî.
Òàê êàê æå âñå-òàêè ðåøàòü óðàâíåíèÿ (íåðàâåíñòâà, ñèñòåìû
íåðàâåíñòâ)?
Óíèâåðñàëüíûõ ðåöåïòîâ íåò. Íàó÷èòüñÿ âûáèðàòü íàèáîëåå
ýôôåêòèâíûå ïóòè ðåøåíèÿ ìîæíî òîëüêî ñ îïûòîì.
Î ñèñòåìàõ è ñîâîêóïíîñòÿõ
óðàâíåíèé è íåðàâåíñòâ
Ïðè ðåøåíèè óðàâíåíèé ìû áóäåì èñïîëüçîâàòü òàê íàçûâàå-
ìûå ñèñòåìû è ñîâîêóïíîñòè óðàâíåíèé è íåðàâåíñòâ.
Ïóñòü äàíî äâà óðàâíåíèÿ
)
(
)
(
11
xgxf
=
è
)
(
)
(
22
xgxf
=
.
(1.6.) Áóäåì ãîâîðèòü, ÷òî çàäàíà ñèñòåìà äâóõ óðàâíåíèé ñ îä-
íîé ïåðåìåííîé, åñëè òðåáóåòñÿ íàéòè âñå çíà÷åíèÿ ïåðåìåííîé, ïðè
êîòîðûõ îáà óðàâíåíèÿ ñèñòåìû îáðàùàþòñÿ â âåðíûå ðàâåíñòâà.
Ðåøåíèåì ñèñòåìû óðàâíåíèé íàçûâàþò çíà÷åíèå ïåðåìåííîé, îáðà-
ùàþùåå îáà óðàâíåíèÿ ñèñòåìû â âåðíûå ÷èñëîâûå ðàâåíñòâà.
Ñòàíäàðòíîå îáîçíà÷åíèå ñèñòåìû:
=
=
)
.
(
)
(
)
,
(
)
(
22
11
xgxf
xgxf
(1.7.) Áóäåì ãîâîðèòü, ÷òî çàäàíà ñîâîêóïíîñòü óðàâíåíèé ñ îä-
íîé ïåðåìåííîé, åñëè òðåáóåòñÿ íàéòè âñå òàêèå çíà÷åíèÿ ïåðåìåí-
íîé, ïðè êàæäîì èç êîòîðûõ õîòÿ áû îäíî èç óðàâíåíèé ñèñòåìû
îáðàùàåòñÿ â âåðíîå ÷èñëîâîå ðàâåíñòâî. Ðåøåíèåì ñîâîêóïíîñòè
óðàâíåíèé íàçûâàþò çíà÷åíèå ïåðåìåííîé, îáðàùàþùåå õîòÿ áû
îäíî èç óðàâíåíèé ñèñòåìû â âåðíîå ÷èñëîâîå ðàâåíñòâî.
Ñòàíäàðòíîå îáîçíà÷åíèå ñîâîêóïíîñòè:
11
22
() ()
() ().
fx gx
fx gx
=
=
Ðåøèòü ñèñòåìó (èëè ñîâîêóïíîñòü) óðàâíåíèé îçíà÷àåò íàé-
òè âñå ðåøåíèÿ èëè äîêàçàòü, ÷òî ñèñòåìà (èëè ñîâîêóïíîñòü) ðå-
øåíèé íå èìååò.
Ïðè ðåøåíèè óðàâíåíèé ïðèìåíÿþò è áîëåå ñëîæíûå êîíñòðóê-
öèè. Íàïðèìåð, ñèñòåìû óðàâíåíèé è íåðàâåíñòâ, ñîâîêóïíîñòè

10
11
Îáùèå ñâåäåíèÿ îá óðàâíåíèÿõ, íåðàâåíñòâàõ è èõ ñèñòåìàõ
Ëåêöèÿ 1
ñèñòåì è òàê äàëåå. Ðåøàÿ óðàâíåíèÿ, ìû â õîäå ïðåîáðàçîâàíèé
áóäåì ïîëó÷àòü íå òîëüêî óðàâíåíèÿ, íî è íåðàâåíñòâà, à òàêæå ñè-
ñòåìû (ñîâîêóïíîñòè) óðàâíåíèé è íåðàâåíñòâ (ñìåøàííûå ñèñòåìû).
Ïðèìåð 7. Ðåøèòå óðàâíåíèå
0
)
1
(
)
2
(
22
=−++
xx
.
Ðåøåíèå. Âñå ñëàãàåìûå ëåâîé ÷àñòè äàííîãî óðàâíåíèÿ íå-
îòðèöàòåëüíû. Ñëåäîâàòåëüíî, ðàâåíñòâî âîçìîæíî, òîëüêî åñëè
êàæäîå èç ñëàãàåìûõ ðàâíî íóëþ.
Òàêèì îáðàçîì,
0
)
1
(
)
2
(
22
=−++
xx
⇔
2
2
(2)0,
(1)0
x
x
+=
−=
⇔
=
−=
.1
,2
x
x
Ïîñëåäíèå äâà ðàâåíñòâà ïðîòèâîðå÷àò äðóã äðóãó, ñëåäîâàòåëü-
íî, ñèñòåìà íå èìååò ðåøåíèé.  ýòîì ñëó÷àå ãîâîðÿò, ÷òî ñèñòåìà
íåñîâìåñòíà.
Îòâåò: íåò ðåøåíèé.
 äàëüíåéøåì ìû íå âñåãäà áóäåì èñïîëüçîâàòü óêàçàííûå îáî-
çíà÷åíèÿ äëÿ ñèñòåì è ñîâîêóïíîñòåé óðàâíåíèé, â íåêîòîðûõ ñëó-
÷àÿõ ìû áóäåì çàïèñûâàòü óðàâíåíèÿ â îäíó ñòðîêó, óêàçûâàÿ ïðè
ýòîì, ÷òî ðàññìàòðèâàåòñÿ ñèñòåìà èëè ñîâîêóïíîñòü.
 ïåðâîé ëåêöèè ìû áóäåì ãîâîðèòü î ðåøåíèè àëãåáðàè÷åñêèõ
óðàâíåíèé (öåëûõ è äðîáíî-ðàöèîíàëüíûõ). Èìåííî ýòîò ðàçäåë ïðåä-
ñòàâëÿåòñÿ èñêëþ÷èòåëüíî âàæíûì äëÿ ïîíèìàíèÿ äàëüíåéøåãî.
Ýòî îáóñëîâëèâàåòñÿ ñëåäóþùèìè ïðè÷èíàìè. Âî-ïåðâûõ, èìåííî
íà ìàòåðèàëå àëãåáðàè÷åñêèõ óðàâíåíèé (ðàöèîíàëüíûõ è äðîáíî-
ðàöèîíàëüíûõ) ëåã÷å âñåãî ïðîâåñòè ïåðâîå çíàêîìñòâî ñ îñíîâíûìè
ïîíÿòèÿìè òåîðèè è âûðàáîòàòü íàâûê ðàáîòû ñ íèìè. Âî-âòîðûõ,
ðåøåíèå çàäà÷ èç äðóãèõ ðàçäåëîâ ýëåìåíòàðíîé ìàòåìàòèêè (â ÷àñ-
òíîñòè, òðèãîíîìåòðè÷åñêèõ, ïîêàçàòåëüíûõ, ëîãàðèôìè÷åñêèõ è
äðóãèõ òðàíñöåíäåíòíûõ óðàâíåíèé, íåðàâåíñòâ è èõ ñèñòåì) ÷àùå
âñåãî ñâîäèòñÿ ê ðåøåíèþ àëãåáðàè÷åñêèõ óðàâíåíèé.
Íàïîìíèì, ÷òî:
(1.8.) Óðàâíåíèå
)
(
)
(
xgxf
=
, ãäå
)
(
xf
,
)
(
xg
ìíîãî÷ëåíû,
íàçûâàþò öåëûì ðàöèîíàëüíûì óðàâíåíèåì. Ðàöèîíàëüíûå óðàâ-
íåíèÿ ìîæíî ïðèâåñòè ê âèäó
-10
++ + =0
n
nn
ax a x a
.
Ñòåïåíü ìíîãî÷ëåíà
n
n
axaxa
+++
10
K
íàçûâàþò ñòåïåíüþ
ðàöèîíàëüíîãî óðàâíåíèÿ. Íàèáîëåå ïðèñòàëüíîå âíèìàíèå â
øêîëüíîì êóðñå ìàòåìàòèêè óäåëÿþò ðàöèîíàëüíûì óðàâíåíèÿì
ïåðâîé è âòîðîé ñòåïåíè. Â íàøåì êóðñå ìû áóäåì ðàññìàòðèâàòü,
êàê ïðàâèëî, óðàâíåíèÿ âûñøèõ ñòåïåíåé.
(1.9.) Óðàâíåíèå,
)()( xgxf =
, ãäå
)(xf
,
)
(
xg
äðîáíûå ðàöèî-
íàëüíûå ôóíêöèè, íàçûâàþò äðîáíî-ðàöèîíàëüíûì óðàâíåíèåì.
Äðîáíî-ðàöèîíàëüíûå óðàâíåíèÿ ìîæíî ïðèâåñòè ê âèäó
1
01
0
++ +
=0
++ +
n
nn
k
nk
ax a x a
bx b x b
.
Îáùèå ìåòîäû ïðåîáðàçîâàíèÿ óðàâíåíèé
Íàïîìíèì íàèáîëåå ÷àñòî èñïîëüçóåìûå ïðåîáðàçîâàíèÿ óðàâ-
íåíèé.
Ðàçëîæåíèå íà ìíîæèòåëè (ðàñùåïëåíèå óðàâíåíèé)
Ìåòîä ðàçëîæåíèÿ íà ìíîæèòåëè îñíîâàí íà ñëåäóþùåé ñõå-
ìå:
,
ÎÄÇ.
()
0
() ()
0
()
0
fx
fx gx
gx
x
=
⋅=⇔
=
∈
Äðóãèìè ñëîâàìè, ïðè ðåøåíèè óðàâíåíèÿ âèäà
0)()( =⋅ xgxf
ìîæíî çàìåíèòü åãî ñîâîêóïíîñòüþ äâóõ áîëåå ïðîñòûõ óðàâíå-
íèé
0
)
(
=
xf
è
0
)
(
=
xg
ïðè óñëîâèè, ÷òî êàæäîå èç íèõ ðàññìàò-
ðèâàåòñÿ íà ÎÄÇ èñõîäíîãî óðàâíåíèÿ.
Çàìåòèì, ÷òî åñëè
)
(
xf
è
)
(
xg
ìíîãî÷ëåíû, òî ÎÄÇ èñ-
õîäíîãî óðàâíåíèÿ è êàæäîãî èç óðàâíåíèé ñîâîêóïíîñòè ñî-
âïàäàåò ñ ìíîæåñòâîì äåéñòâèòåëüíûõ ÷èñåë, ïîýòîìó äëÿ ðà-
öèîíàëüíûõ óðàâíåíèé ñõåìà ðàçëîæåíèÿ íà ìíîæèòåëè âû-
ãëÿäèò ïðîùå:
() 0
() () 0
() 0.
fx
fx gx
gx
=
⋅=⇔
=
Ïðèìåð 8. Ðåøèòå óðàâíåíèå
064164
23
=+−−
xxx
.
Ðåøåíèå. Ðàçëîæèì ëåâóþ ÷àñòü óðàâíåíèÿ íà ìíîæèòåëè ìåòîäîì
ãðóïïèðîâêè. Ïîëó÷èì:
0
)
4
(
16
)
4
(
2
=−−−
xxx
⇔
0
)
16
)(
4
(
2
=−−
xx
⇔
0
)
4
(
)
4
(
2
=+−
xx
.
Îòâåò:
4±
.

12
13
Îáùèå ñâåäåíèÿ îá óðàâíåíèÿõ, íåðàâåíñòâàõ è èõ ñèñòåìàõ
Ëåêöèÿ 1
Ïðèìåð 9. Ðåøèòå óðàâíåíèå
9
13
3
2
2
=−
x
x
.
Ðåøåíèå. Ïåðåïèøåì óðàâíåíèå:
+=−
3
21
9
4
2
x
x
x
⇔
+=
+
−
3
21
3
2
3
2
x
x
xx
⇔
0
1
3
2
3
2
=
−−
+
x
xx
,
÷òî ðàâíîñèëüíî ñîâîêóïíîñòè óðàâíåíèé
2
0
3
12
.
3
x
x
x
+=
−=
Îòâåò:
3
2
−
,
3
101 ±
.
Ïðè ðàçëîæåíèè íà ìíîæèòåëè ëåâîé ÷àñòè öåëîãî ðàöèîíàëü-
íîãî óðàâíåíèÿ ïðèìåíÿþò ñëåäóþùóþ òåîðåìó.
Òåîðåìà 4. Åñëè
0
x
êîðåíü óðàâíåíèÿ
0)( =xf
, ãäå
)(xf
ìíîãî÷ëåí ñòåïåíè n, òî
)
(
)
(
)
(
0
xgxxxf
⋅−=
, ïðè÷åì
)
(
xg
ìíî-
ãî÷ëåí ñòåïåíè n1.
Äîêàçàòåëüñòâî. Ïîêàæåì, ÷òî
)
(
xf
ìîæíî ïðåäñòàâèòü â âèäå
)
(
)
(
0
xgxx
⋅−
.
Ïóñòü
01
()
n
n n
fx ax ++a x+a
=
è
0
x
êîðåíü óðàâíåíèÿ
0)( =xf
,
òîãäà
0
)
(
0
=
xf
, è
00010
() ( ) () ( ) ( )
nn
n
f x f x f x a x x ++a xx
==
.
Ïîñêîëüêó
)
)(
(
1
0
2
00
21
00
−−−−
+⋅++⋅+−=−
nnnnnn
xxxxxxxxxx
K
,
òî â ïðàâîé ÷àñòè ðàâåíñòâà ìîæíî âûíåñòè çà ñêîáêè âûðàæåíèå
0
xx
−
, à âûðàæåíèå â ñêîáêàõ ìíîãî÷ëåí ñòåïåíè n 1.
Ïðèìåð 10. Ðåøèòå óðàâíåíèå
010
3
=−+
xx
.
Ðåøåíèå. Ïîäñòàíîâêîé óáåäèìñÿ, ÷òî 2 êîðåíü óðàâíåíèÿ.
Ðàçëîæèì ëåâóþ ÷àñòü óðàâíåíèÿ íà ìíîæèòåëè:
3322
22
+10
(
2
)
+
(
24
)
+
(
510
)
(
2
)
+2
(
2
)
+5
(
2
)(
2
)(
+2 +5
)
xx x x x x x
xx xx x x x x
==
==
.
Ïîëó÷èì óðàâíåíèå:
0
)
52
)(
2
(
2
=++−
xxx
⇔
2
20
250.
x
xx
−=
++=
Âòîðîå óðàâíåíèå ñîâîêóïíîñòè êîðíåé íå èìååò.
Îòâåò: 2.
Ðàöèîíàëüíûå êîðíè óðàâíåíèÿ
Êàêèì æå îáðàçîì ìîæíî «óãàäàòü êîðåíü»? Ìîæíî ïîïû-
òàòüñÿ âîñïîëüçîâàòüñÿ ñëåäóþùåé òåîðåìîé.
Òåîðåìà 5. Åñëè
0
x
öåëûé êîðåíü óðàâíåíèÿ
0
)
(
=
xf
, ãäå
f(x) ìíîãî÷ëåí ñ öåëûìè êîýôôèöèåíòàìè, ñâîáîäíûé ÷ëåí êî-
òîðîãî íå ðàâåí 0, òî
0
x
äåëèòåëü ñâîáîäíîãî ÷ëåíà.
Äîêàçàòåëüñòâî. Ïóñòü
01
()
n
n n
fx ax ++a x+a
=
è
0
)
(
0
=
xf
.
Òî åñòü
00 10
n
nn
ax a x a
+…+ =
, îòêóäà ñëåäóåò, ÷òî
1
00
(
n
ax
−
−++
K
10
)
nn
ax a
−
+=, ÷òî îçíà÷àåò, ÷òî
0
x
äåëèòåëü
n
a
.
Ïðèìåð 11. Íàéäèòå öåëûå êîðíè óðàâíåíèÿ
016249
23
=−+−
xxx
.
Ðåøåíèå. Äåëèòåëè ñâîáîäíîãî ÷ëåíà:
1±
,
2±
,
4±
,
8±
,
16±
.
Ïîäñòàíîâêîé ìîæíî óáåäèòüñÿ, ÷òî 1 è 4 êîðíè óðàâíåíèÿ.
Îòâåò: 1; 4.
Ìîæíî äîêàçàòü è áîëåå îáùóþ òåîðåìó.
Òåîðåìà 6. Åñëè
n
m
x
=
0
ðàöèîíàëüíûé êîðåíü óðàâíåíèÿ
0
)
(
=
xf
, ãäå
)
(
xf
ìíîãî÷ëåí ñ öåëûìè êîýôôèöèåíòàìè, òî m
äåëèòåëü ñâîáîäíîãî ÷ëåíà, à n äåëèòåëü ñòàðøåãî ÷ëåíà.
Äîêàæèòå ýòó òåîðåìó ñàìîñòîÿòåëüíî.
Ïðèìåð 12. Íàéäèòå ðàöèîíàëüíûå êîðíè óðàâíåíèÿ
01334
23
=−++
xxx
.
Ðåøåíèå. Öåëûå è ðàöèîíàëüíûå êîðíè ñîäåðæàòñÿ ñðåäè ÷è-
ñåë:
1±
,
2
1
±
,
4
1
±
.
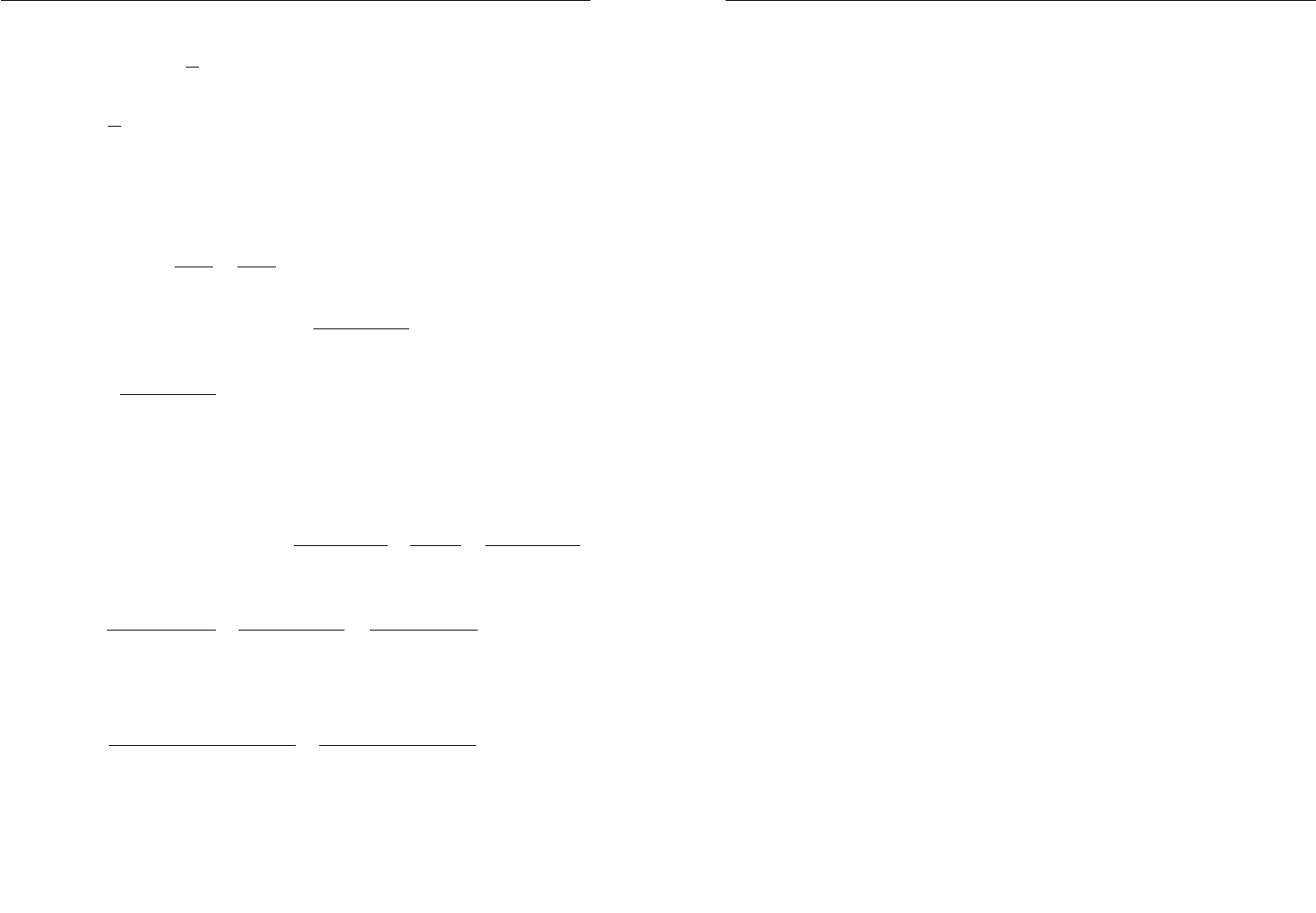
14
15
Îáùèå ñâåäåíèÿ îá óðàâíåíèÿõ, íåðàâåíñòâàõ è èõ ñèñòåìàõ
Ëåêöèÿ 1
Ïîäñòàíîâêà ïîêàçûâàåò, ÷òî åäèíñòâåííûé ðàöèîíàëüíûé êî-
ðåíü óðàâíåíèÿ
4
1
=
x
.
Îòâåò:
4
1
.
«Èçáàâëåíèå» îò çíàìåíàòåëÿ
Íåðåäêî ìîæíî óïðîñòèòü óðàâíåíèå, óìíîæèâ îáå åãî ÷àñòè
íà îáùèé çíàìåíàòåëü åãî äðîáíûõ ÷ëåíîâ.
Ñõåìà ìåòîäà:
≠
=
⇔=
.0
)
(
)
,
(
)
(
)
(
)
(
)
(
)
(
xp
xgxf
xp
xg
xp
xf
Ïðèìåð 13. Ðåøèòå óðàâíåíèå
0
34
23
2
2
=
+−
+−
xx
xx
.
Ðåøåíèå.
0
34
23
2
2
=
+−
+−
xx
xx
⇔
≠+−
=+−
.034
,023
2
2
xx
xx
Êîðíè óðàâíåíèÿ
023
2
=+−
xx
:
1
1
=
x
,
2
2
=
x
.
Êîðåíü 1 ïîñòîðîííèé, òàê êàê
03141
2
=+⋅−
.
Îòâåò: 2.
Ïðèìåð 14. Ðåøèòå óðàâíåíèå
34
1
1
5
32
2
222
+−
=
−
−
+
−−
xxx
x
xx
.
Ðåøåíèå. Ïðåîáðàçóåì çíàìåíàòåëè â ïðîèçâåäåíèå:
)
3
)(
1
(
1
)
1
)(
1
(
5
)
3
)(
1
(
2
−−
=
−+
−
+
−+
xxxx
x
xx
.
Ñîñòàâëÿåì îáùèé çíàìåíàòåëü:
)
3
)(
1
)(
1
(
−−+
xxx
.
Ïðåîáðàçóåì:
)
3
)(
1
)(
1
(
1
)
3
)(
1
)(
1
(
)
3
)(
5
(
)
1
(
2
−+−
+
=
−+−
−−+−
xxx
x
xxx
xxx
.
Óðàâíåíèå ðàâíîñèëüíî ñèñòåìå:
≠−
≠+
≠−
+=+−
.03
,01
,01
,1136
2
x
x
x
xxx
⇔
≠
±≠
=+−
.3
,1
,0127
2
x
x
xx
Êîðíè êâàäðàòíîãî óðàâíåíèÿ: 4 è 3.
Êîðåíü 3 ïîñòîðîííèé, ïîñêîëüêó
3≠
x
.
Îòâåò: 4.
Çàìåíà ïåðåìåííîé â óðàâíåíèè
Ìåòîä çàìåíû ïåðåìåííîé (èëè, èíà÷å, ìåòîä ââåäåíèÿ íîâîãî
íåèçâåñòíîãî) ñîñòîèò â ñëåäóþùåì. Ïðåäïîëîæèì, ÷òî óðàâíå-
íèå
)
(
)
(
xpxf
=
óäàëîñü ïåðåïèñàòü â âèäå
))
(
(
))
(
(
xgpxgf
=
. Ðåøå-
íèå óðàâíåíèÿ
)
(
)
(
xpxf
=
ïðîâåäåì â äâà ýòàïà:
1) Áóäåì ñ÷èòàòü, ÷òî
uxg
=
)
(
, ðåøèì óðàâíåíèå
=
() ()
fu pu
.
Ïîëó÷èì: u
1
, u
2
, ..., u
n
êîðíè óðàâíåíèÿ =
() ()
fu pu
.
2) Ïîñëåäîâàòåëüíî ðåøèì óðàâíåíèÿ
1
)(
uxg
=
,
2
)(
uxg
=
, …,
n
uxg
=
)
(
.
Ïîëó÷åííûå êîðíè è áóäóò êîðíÿìè óðàâíåíèÿ
)
(
)
(
xpxf
=
.
Ñõåìà ìåòîäà:
1
2
()
()
(()) (())
() ,
n
gx u
gx u
fgx pgx
gx u
=
=
=⇔
=
K
12
ãäå ,,, êîðíè óðàâíåíèÿ () ().
n
uu u fu pu
=
K
Ââåäåíèå íîâîé ïåðåìåííîé ïîçâîëÿåò «ðàçáèòü çàäà÷ó íà ïîä-
çàäà÷è», òî åñòü âìåñòî îäíîãî ñëîæíîãî ðåøàòü íåñêîëüêî ïðî-
ñòûõ óðàâíåíèé.
Ïðèìåð 15. Ðåøèòå óðàâíåíèå
12
)
2
)(
1
(
22
=++++
xxxx
.
Ðåøåíèå. Ïóñòü
1
2
++=
xxu
, òîãäà èñõîäíîå óðàâíåíèå ïðè-
íèìàåò âèä
12
)
1
(
=+
uu
, îòêóäà
012
2
=−+
uu
,
3
1
=
u
,
4
2
−=
u
.
Ðàññìîòðèì äâà ñëó÷àÿ:
1)
31
2
=++
xx
,
02
2
=−+
xx
, îòêóäà
2
1
−=
x
,
1
2
=
x
.
2)
41
2
−=++ xx
,
05
2
=++
xx
. Óðàâíåíèå êîðíåé íå èìååò.
Îòâåò: 2; 1.
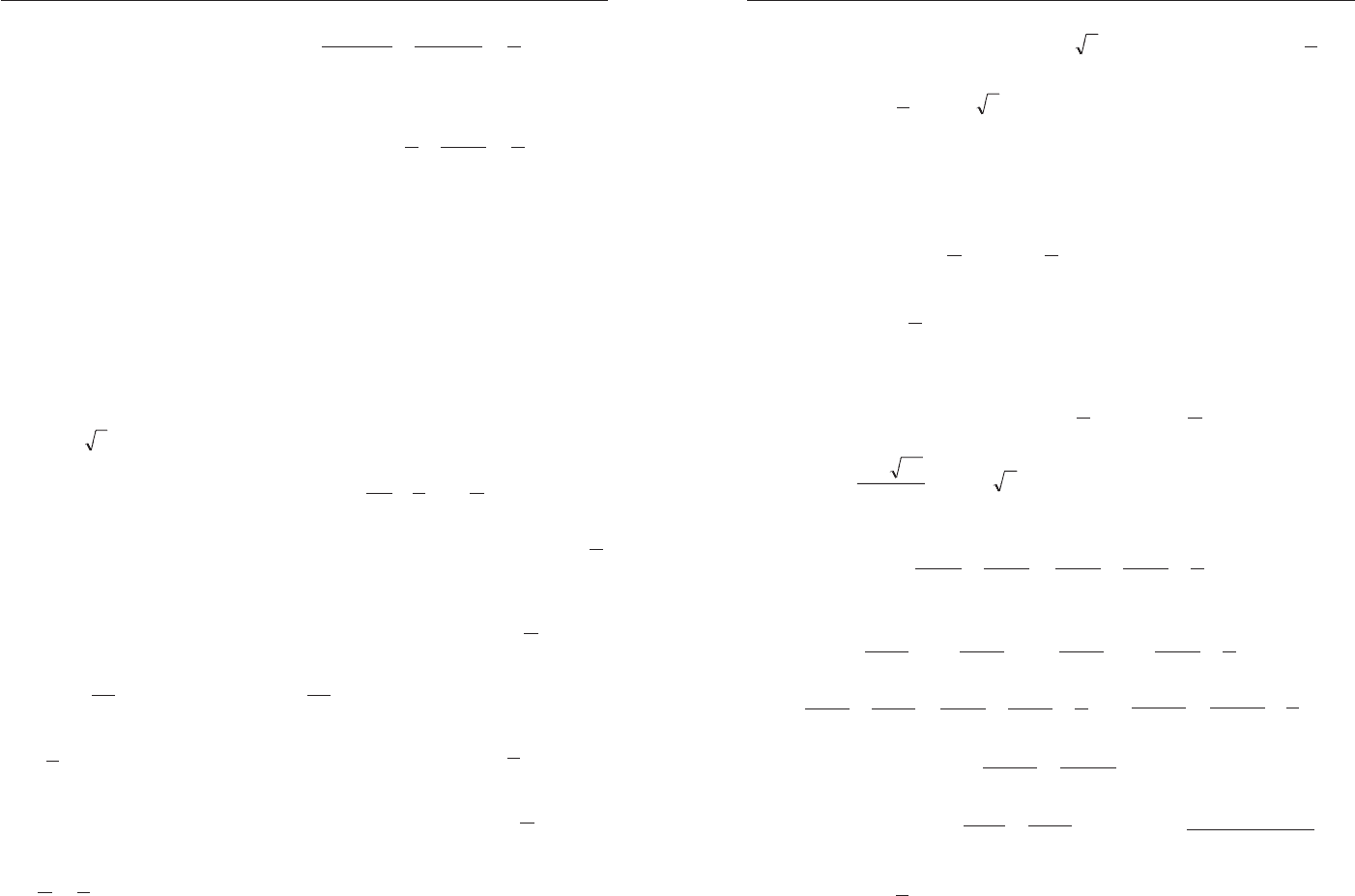
16
17
Îáùèå ñâåäåíèÿ îá óðàâíåíèÿõ, íåðàâåíñòâàõ è èõ ñèñòåìàõ
Ëåêöèÿ 1
Ïðèìåð 16. Ðåøèòå óðàâíåíèå
5
4
)
2
(
1
)
4
(
1
2
=
+
−
+
x
xx
.
Ðåøåíèå. Ïóñòü
xxu 4
2
+= .
Ïåðåïèøåì èñõîäíîå óðàâíåíèå â âèäå
5
4
4
11
=
+
−
uu
. Äîìíî-
æèâ îáå ÷àñòè óðàâíåíèÿ íà îáùèé çíàìåíàòåëü, ïîëó÷èì ñèñòåìó
−≠≠
=−+
.4,0
,054
2
uu
uu
Ðåøåíèå ñèñòåìû:
1
1
=
u
,
5
1
−=
u
.
Îñòàëîñü ðåøèòü ñîâîêóïíîñòü óðàâíåíèé
=++
=−+
.054
,014
2
2
xx
xx
Âòîðîå óðàâíåíèå ñîâîêóïíîñòè êîðíåé íå èìååò, êîðíè ïåðâî-
ãî:
52 ±−
.
Ïðèìåð 17. Ðåøèòå óðàâíåíèå
5
1
2
11
2
2
=
−++
x
x
x
x
.
Ðåøåíèå. Çàìåòèì, ÷òî åñëè a êîðåíü óðàâíåíèÿ, òî
a
1
−
òàêæå êîðåíü óðàâíåíèÿ. Â ýòîì ëåãêî óáåäèòüñÿ ïîäñòàíîâêîé.
 òàêèõ ñëó÷àÿõ ïîëåçíî ïîïðîáîâàòü çàìåíó:
x
xu
1
−=
, òîãäà
2
1
2
22
−+=
x
xu
,
2
22
1
2
x
xu
+=+
. Ïîëó÷èì óðàâíåíèå:
03
2
1
2
=−+
uu
,
062
2
=−+
uu
, êîðíè êîòîðîãî 2 è
2
3
.
Îñòàëîñü ðåøèòü ñîâîêóïíîñòü óðàâíåíèé
2
1
−=−
x
x
è
2
31
=−
x
x
, ÷òî ðàâíîñèëüíî:
2
2
210
2320.
xx
xx
+−=
−−=
Êîðíè ïåðâîãî óðàâíåíèÿ:
21 ±−
, êîðíè âòîðîãî: 2;
2
1
−
.
Îòâåò: 2;
2
1
−
;
21 ±−
.
Ïðèìåð 18. Ðåøèòå óðàâíåíèå
222
24
)
32
)(
33
(
xxxxx
=+−++
.
Ðåøåíèå. Çàìåòèì, ÷òî
0=
x
íå ÿâëÿåòñÿ ðåøåíèåì äàííîãî
óðàâíåíèÿ. Ðàçäåëèì îáå ÷àñòè óðàâíåíèÿ íà
2
x
.
Ïîëó÷èì:
24
3
2
3
3 =
+−
++
x
x
x
x
.
Ïóñòü
x
xu
3
+=
, òîãäà
24
)
2
)(
3
(
=−+
uu
,
030
2
=−+
uu
, îò-
êóäà
5
1
=
u
,
6
2
−=
u
.
Îñòàëîñü ðåøèòü óðàâíåíèÿ
5
3
=+
x
x
è
6
3
−=+
x
x
.
Îòâåò:
2
135 ±
,
63 ±−
.
Ïðèìåð 19. Ðåøèòå óðàâíåíèå
3
8
2
8
2
8
1
4
1
4
−
+
−
+
−
+
=
+
−
+
−
+
x
x
x
x
x
x
x
x
.
Ðåøåíèå. Ïðåîáðàçóåì èñõîäíîå óðàâíåíèå:
3
8
2
10
1
2
10
1
1
5
1
1
5
1 −
+
−+
−
+=
+
−+
−
+
xxxx
⇔
⇔
3
8
2
10
2
10
1
5
1
5
−
+
−
−
=
+
−
−
xxxx
⇔
3
8
4
40
1
10
22
−
−
=
−
xx
⇔
⇔
4
4
60
1
15
22
−
−
=
−
xx
.
Ïóñòü
yx
=
2
, òîãäà
4
4
60
1
15
−
−
=
−
yy
, îòêóäà
0
)
4
)(
1
(
16654
2
=
−−
+−
yy
yy
è
16
1
=
y
,
4
1
2
=
y
.
Èñõîäíîå óðàâíåíèå èìååò ÷åòûðå êîðíÿ.
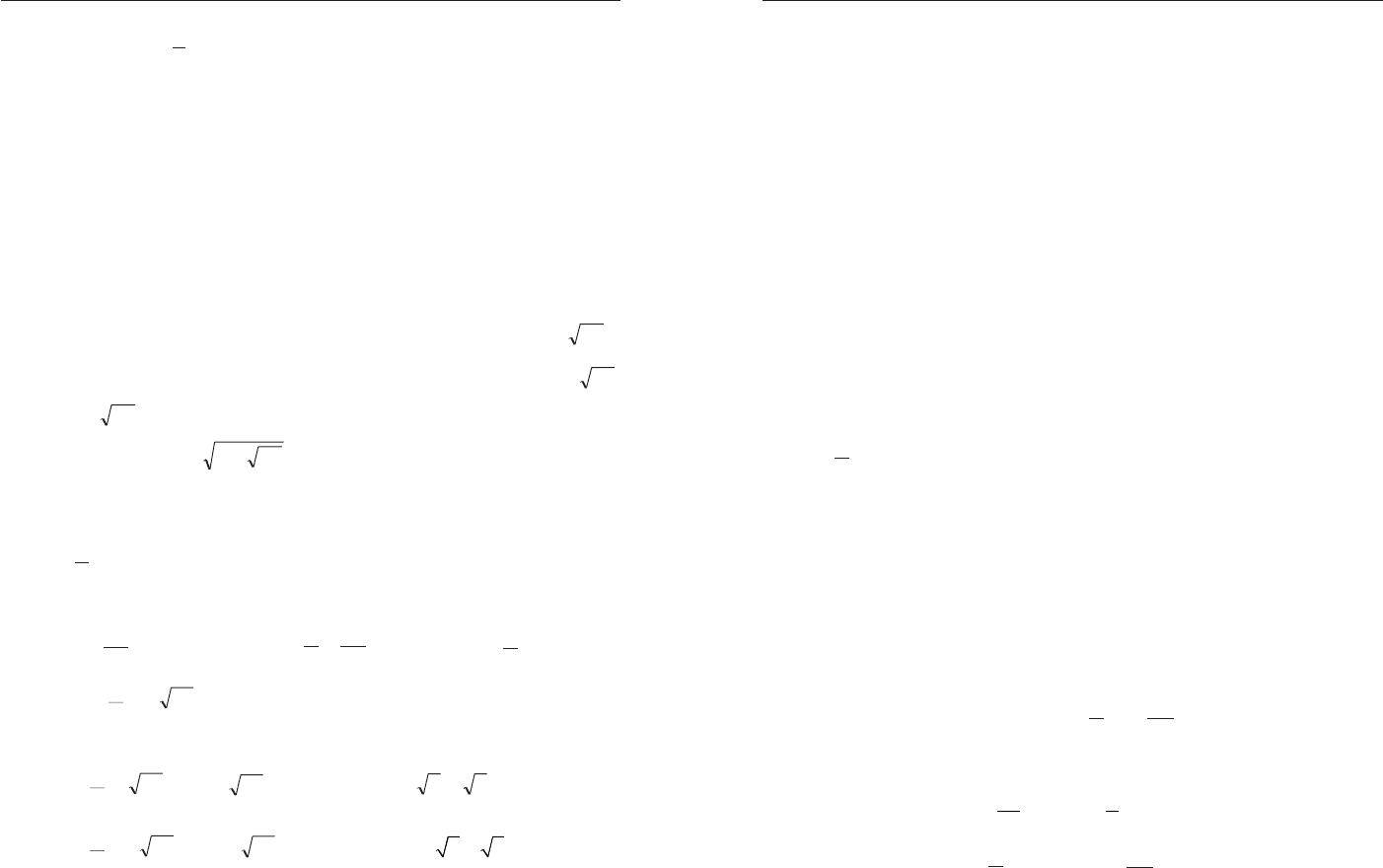
18
19
Îáùèå ñâåäåíèÿ îá óðàâíåíèÿõ, íåðàâåíñòâàõ è èõ ñèñòåìàõ
Ëåêöèÿ 1
Îòâåò:
4±
,
2
1
±
.
Ðàññìîòðèì íåêîòîðûå ñïåöèàëüíûå ñëó÷àè çàìåíû â àëãåáðà-
è÷åñêèõ óðàâíåíèÿõ.
Áèêâàäðàòíûå óðàâíåíèÿ
Óðàâíåíèÿ âèäà
0
24
=++
cbxx
, áóäåì íàçûâàòü áèêâàäðàò-
íûìè óðàâíåíèÿìè.
Ïåðâûé ñïîñîá. Áèêâàäðàòíîå óðàâíåíèå ìîæíî çàìåíîé
2
xy
=
ñâåñòè ê êâàäðàòíîìó óðàâíåíèþ
0
2
=++
cbyy
.
Ïðèìåð 20. Ðåøèòå óðàâíåíèå
0110
24
=+−
xx
.
Ðåøåíèå. Ïóñòü
2
xy
=
,
0110
2
=+−
yy
, òîãäà
245
2,1
±=
y
.
Ðåøèâ ñîâîêóïíîñòü íåïîëíûõ êâàäðàòíûõ óðàâíåíèé
245
2
+=
x
è
245
2
−=
x
, ïîëó÷èì îòâåò.
Îòâåò:
245
4,3,2,1
±±=
x
.
Ìîæíî äåéñòâîâàòü èíà÷å.
Âòîðîé ñïîñîá. Ïðè
0>
c
, ìîæíî âîñïîëüçîâàòüñÿ çàìåíîé
x
xy
1
+=
.
Ðàçäåëèì îáå ÷àñòè óðàâíåíèÿ íà õ
2
. Ïîëó÷èì:
010
1
2
2
=−+
x
x
,
012
11
2
2
2
=−+⋅+
x
x
xx
,
12
1
2
=
+
x
x
,
îòêóäà
12
1
±=+
x
x
.
Ðåøèì ïîëó÷åííûå óðàâíåíèÿ:
1)
12
1
=+
x
x
,
0112
2
=+−
xx
,
23
2,1
±=
x
.
2)
12
1
−=+
x
x
,
0112
2
=++
xx
,
3,4
32
x =− ±
.
Èíòåðåñíî, ÷òî ýòî òå æå ñàìûå êîðíè, ÷òî è â ïðåäûäóùåì
ïðèìåðå.
Ïðèìåð 21. Ðåøèòå óðàâíåíèå
82
)
3
(
)
1
(
44
=++−
xx
.
Ðåøåíèå. Ïóñòü
1+=
xy
, òîãäà èñõîäíîå óðàâíåíèå ïðèíè-
ìàåò âèä
82
)
2
(
)
2
(
44
=++−
yy
, îíî ðàâíîñèëüíî óðàâíåíèþ
02524
24
=−+
yy
, êîòîðîå óæå ìîæíî ðàññìàòðèâàòü êàê áè-
êâàäðàòíîå óðàâíåíèå. Ðåøèòå åãî ñàìîñòîÿòåëüíî.
Îòâåò: 0 è 2.
Ñèììåòðè÷åñêèå óðàâíåíèÿ
Óðàâíåíèÿ âèäà
0
01
1
10
=++++++++
−−
axaxaxaxaxa
k
k
kn
k
nn
KKK
,
ãäå êîýôôèöèåíòû ÷ëåíîâ, ðàâíî îòñòîÿùèõ îò êîíöîâ, ðàâíû
ìåæäó ñîáîé, íàçûâàþò ñèììåòðè÷åñêèìè óðàâíåíèÿìè.
Ñèììåòðè÷åñêèå óðàâíåíèÿ îáëàäàþò ñëåäóþùèìè ñâîéñòâàìè:
1) ñèììåòðè÷åñêîå óðàâíåíèå íå÷åòíîé ñòåïåíè èìååò êîðåíü
1−=
x
, â ÷åì ìîæíî óáåäèòüñÿ íåïîñðåäñòâåííîé ïîäñòàíîâêîé;
2) óðàâíåíèå ÷åòíîé ñòåïåíè 2n ñ ïîìîùüþ ïîäñòàíîâêè
x
xv
1
+=
ñâîäèòñÿ ê óðàâíåíèþ ñòåïåíè n.
Ïðèìåð 22. Ðåøèòå óðàâíåíèå
025131352
2345
=++−−+
xxxxx
.
Ðåøåíèå. Çàìåòèì, ÷òî
1−=
x
êîðåíü èñõîäíîãî óðàâíåíèÿ.
Ïóñòü
1−≠x . Ðàçäåëèì ëåâóþ ÷àñòü óðàâíåíèÿ íà
1+x
è ïîëó-
÷èì ñèììåòðè÷åñêîå óðàâíåíèå ÷åòâåðòîé ñòåïåíè:
0231632
234
=++−+
xxxx
.
Ðàçäåëèì îáå ÷àñòè óðàâíåíèÿ íà õ
2
:
0
1
2
1
31632
2
2
=⋅+⋅+−+
x
x
xx
,
è ñãðóïïèðóåì ÷ëåíû óðàâíåíèÿ:
2
2
11
23160
xx
x
x
+++−=
.
Ïóñòü òåïåðü
x
xt
1
+=
, òîãäà
2
1
2
2
2
−=+
t
x
x
, è ïîñëå ïðåîá-
ðàçîâàíèé ïîëó÷èì êâàäðàòíîå óðàâíåíèå
02032
2
=−+
tt
.
