Cold and Hot Forging: Fundamentals and Applications / Edited by Taylan Altan, Gracious Ngaile, Gangshu Shen

Подождите немного. Документ загружается.

Inverse Analysis for Simultaneous Determination of Flow Stress and Friction / 87

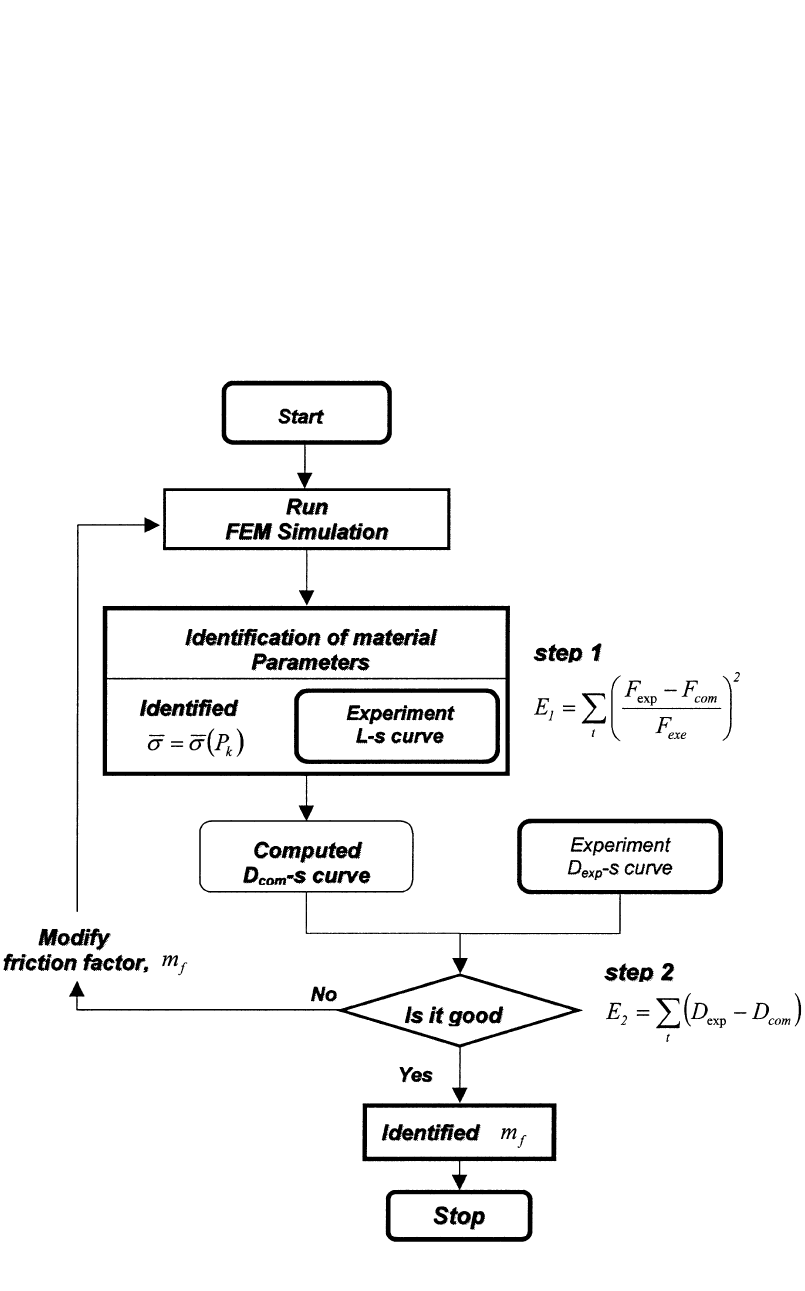
Fig. 8.3

Flow chart of simultaneous determination of ﬂow stress and friction. L-s, load versus stroke; D-s, bulge diameter versus

stroke; m

, friction factor

obtained from the ring compression test. The in-

vestigated material was assumed to follow

strain-hardening behavior and the following

power-law-type ﬂow stress equation was consid-

ered.

¯r ⳱ K¯e (Eq 8.6)

Therefore, a set of material parameters deﬁned

by P

⳱ {K,n} and friction factor m

are the

unknown parameters that have to be identiﬁed.

Two experimental quantities: (1) the measured

load-stroke curve and (2) the maximum diame-

ter of the specimen at the end of stroke were

used as experimental values in the inverse anal-

ysis.

8.5.2 Experiment

Aluminum rings made from Aluminum 6061-

T6 with 2.13 in. OD ⳯ 1.06 in. ID ⳯ 0.71 in.

height (54 mm OD ⳯ 27 mm ID ⳯ 18 mm

height) were compressed to various reductions

88 / Cold and Hot Forging: Fundamentals and Applications

Fig. 8.4 Compressed ring samples

Table 8.2 Percent decrease in ID of ring

Reduction in height, % Decrease in ID of ring, %

7.2 ⳮ1.48

22.2 ⳮ2.96

40.0 ⳮ1.85

Table 8.3 Predicted inverse analysis results

(ring test)

Decrease in ID

K-value, MPa

Friction (m

) of ring, % ksi MPa n-value

0.2 Ⳮ0.5 65 446 0.073

0.15 ⳮ5.9 67 459 0.076

0.175 ⳮ1.7 66 452 0.074

Fig. 8.5

Comparison of computed and experimental load-

stroke curves (ring test)

rized in Table 8.3. Three inverse analyses were

conducted by varying the friction factor from

0.15 to 0.2. As initial guesses of material param-

eters, K ⳱ 430 (MPa) and n ⳱ 0.1 were used

for every case. When the friction factor 0.175

was assumed, the inverse analysis prediction

produced only 8.1% underestimation in ID com-

parison of the ring. Thus, a combination of fric-

tion factor m

⳱ 0.175 and ﬂow stress ⳱¯r

(MPa) gives the best minimum for the

0.074

452¯e

objective function. As can be seen in Fig. 8.5,

after four optimization iterations, computed and

experimental loads are nearly identical.

8.5.4 Veriﬁcation of the

Determined Friction Factor

To verify the accuracy of determined friction

factor, FEM simulations using the determined

ﬂow stress with friction factor of 0.175 were

conducted for various friction factors. Thus, the

ring calibration curves were generated as shown

in Fig. 8.6. It is seen that measurements match

well the curve obtained with the friction factor

of 0.182, which is very close to 0.175.

8.5.5 Veriﬁcation of the

Determined Flow Stress

In order to verify the ﬂow stress determined

with friction factor by the inverse analysis, the

aluminum cylinders with a 30 mm diam ⳯ 30

mm height were upset to 38% reduction in

height. To minimize interface friction, the inter-

face was lubricated with Ecoform lubricant

made by Fuchs. As shown in Fig. 8.7, the lu-

brication nearly eliminated bulging in upsetting

of cylinder. Using the measured load-stroke

curve, ﬂow stress ⳱ (MPa) was ob-

0.067

¯r 437¯e

tained. The difference between the ﬂow stress

in height. The rings were lubricated with Teﬂon

spray on all surfaces of the samples and on the

top and bottom dies. In order to observe the in-

ternal diameter variation the test was stopped at

reductions of 7.2, 22.2, and 40%. Figure 8.4

shows the compressed ring samples, and Table

8.2 shows the decrease in ID of the ring at dif-

ferent reductions.

8.5.3 Determination of

Flow Stress and Friction

The results of identifed parameters (K-value

and n-value) in the ﬂow stress equation and fric-

tion factor by the inverse analysis are summa-

Inverse Analysis for Simultaneous Determination of Flow Stress and Friction / 89

Fig. 8.7 Compressed ring samples

data obtained in ring and cylinder compression

tests is about 3.3% in K-value and 9.5% in n-

value, respectively.

REFERENCES

[Boyer & Massoni, 2001]: Boyer, B., Massoni,

E., “Inverse Analysis for Identiﬁcation of Pa-

rameters During Thermo-Mechanical Tests,”

Simulation of Materials Processing: Theory,

Method and Applications, K.-I. Mori, Ed.,

2001, p 281–284.

[Chenot et al., 1996]: Chenot, J., Massoni, E.,

Fourment, L., “Inverse Problems in Finite

Element Simulation of Metal Forming Pro-

cesses,” Eng. Comput., Vol 13 (No. 2/3/4),

1996, p 190–225.

[Cho et al., 2003]: Cho, H., Ngaile, G., “Si-

multaneous Determination of Flow Stress and

Interface Friction by Finite Element Based In-

verse Analysis Technique,” Ann. CIRP, Vo l

52/1, 2003, p 221–224.

[Dahl et al., 1999]: Dahl, C., Vazquez, V., Al-

tan, T., “Determination of Flow Stress of 1524

Steel at Room Temperature Using the Com-

pression Test,” Engineering Research Center

for Net Shape Manufacturing, ERC/NSM-99-

R-22.

[Pietrzyk et al., 2001]: Pietrzyk, M., Szyndler,

D., Hodgson, P.D., “Identiﬁcation of Param-

eters in the Internal Variable Constitutive

Model and Friction Model for Hot Forming

of Steels,” Simulation of Materials Process-

ing: Theory, Method and Applications, Mori,

Ed., 2001, p 281–284.

[Zhiliang et al., 2002]: Zhiliang, Z., Xinbo, L.,

Fubao, Z., “Determination of Metal Material

Flow Stress by the Method of C-FEM,” J.

Mater. Process. Technol., Vol 120, 2002, p

144–150.

Fig. 8.6

Ring calibration curves obtained with ⳱¯r

(MPa)

0.074

452¯e

CHAPTER 9

Methods of

Analysis for Forging Operations

Manas Shirgaokar

9.1 Introduction

The major process variables involved in forg-

ing can be summarized as: (a) the billet material

properties, (b) the tooling/dies, (c) tool/work-

piece interface conditions, (d) forging equip-

ment, (e) mechanics of the deformation zone,

and (f) the environmental conditions. The major

objectives of analyzing any forging operation

are:

●

Establish the kinematic relationships (shape,

velocities, strain rates, and strain) between

the undeformed part (billet or preform) and

the deformed part (ﬁnal forged product), i.e.,

predict the metal ﬂow during the forming

operation.

●

Establish the limits of formability or produ-

cibility, i.e., determine whether it is possible

to perform the forming operation without

causing any surface or internal failures

(cracks or folds) in the deforming material.

●

Predict the stresses, the forces, and the en-

ergy necessary to carry out the forming

operation. This information is necessary for

tool design and for selecting the appropriate

equipment, with adequate force and energy

capabilities, to perform the forming opera-

tion.

There are several different approximate meth-

ods, both analytical and numerical, for analyzing

forging processes. None of these methods is per-

fect because of the assumptions made in devel-

oping the mathematical approach. In addition,

every method of analysis requires as input:

●

A description of the material behavior under

the process conditions, i.e., the ﬂow stress

data

●

A quantitative value to describe the friction,

i.e., the friction factor, m, or the friction co-

efﬁcient, l.

These two quantities themselves (ﬂow stress and

friction) must be determined by experiment and

are difﬁcult to obtain accurately. Thus, any er-

rors in ﬂow stress measurement or uncertainties

in the value of the friction factor are expected to

inﬂuence the accuracy of the results of the anal-

ysis.

Forging processes can be analyzed by several

methods including the slab method, the slip-line

method, the visioplasticity method, the upper-

bound method, ﬁnite difference method, and the

ﬁnite element method. The capabilities and char-

acteristics of these methods are summarized in

Table 9.1 [Altan et al., 1979].

In the slab method, the workpiece being de-

formed is decomposed into several slabs. For

each slab, simplifying assumptions are made

mainly with respect to stress distributions. The

resulting approximate equilibrium equations are

solved with imposition of stress compatibility

between slabs and boundary tractions. The ﬁnal

result is a reasonable load prediction with an ap-

proximate stress distribution [Kobayashi et al.,

1989].

The slip-line ﬁeld method is used in plane

strain for perfectly plastic materials (constant

Cold and Hot Forging Fundamentals and Applications

Taylan Altan, Gracious Ngaile, Gangshu Shen, editors, p91-105

DOI:10.1361/chff2005p091

www.asminternational.org

92 / Cold and Hot Forging: Fundamentals and Applications

Table 9.1 Characteristics of various methods of analysis

Input

Output

Method Flow stress Friction

Velocity

ﬁeld

Stress

ﬁeld

Temperature

ﬁeld

Stresses

on tools Comments

Slab Average (a)(b) No Yes No Yes Ignores redundant work

Uniform energy Average (b) No No No Average Redundant work can be included approximately

Slip line Average (a)(b) Yes Yes No Yes Valid for plane-strain problems

Upper bound Distribution (b) Yes No No Average Gives upper bound on loads, can determine

free boundaries

Hill’s Distribution (a)(b) Yes No No Average Can treat 3-D problems

Finite difference Distribution (a)(b) Yes Yes Yes Yes Requires considerable computer time

Finite element Distribution (a)(b) Yes Yes Yes Yes Same as above

Matrix Distribution (a)(b) Yes Yes Yes Yes Treats rigid/plastic material

Weighted residuals Distribution (a)(b) Yes Yes Yes Yes Very general approach

(a) s ⳱ lr

.(b)s ⳱ . Source: [Altan et al., 1979]m¯r/3

冪

yield stress) and uses the hyperbolic properties

that the stress equations have in such cases. The

construction of slip-line ﬁelds, although produc-

ing an “exact” stress distribution, is still quite

limited in predicting results that give good cor-

relations with experimental work. From the

stress distributions, velocity ﬁelds can be cal-

culated through plasticity equations [Kobayashi

et al., 1989].

The visioplasticity method [Thomsen et al.,

1954] combines experiment and analysis. A grid

is imprinted on the metal or modeling substance

before deformation starts. Pictures taken at small

intervals during processing enable the investi-

gator to construct a ﬂow pattern. After the ve-

locity vectors have been determined from an ac-

tual test, strain rates are calculated and the stress

distributions are obtained from plasticity equa-

tions. The method can be used to obtain reliable

solutions in detail for processes in which the ex-

perimental determination of the velocity vectors

was possible.

The upper-bound method requires the

“guessing” of admissible velocity ﬁelds (i.e.,

satisfying the boundary conditions), among

which the best one is chosen by minimizing total

potential energy. Information leading to a good

selection of velocity ﬁelds comes from experi-

mental evidence and experience. This method,

with experience, can deliver fast and relatively

accurate prediction of loads and velocity distri-

butions [Kobayashi et al., 1989].

All of the above highlighted methods of anal-

ysis fail to consider temperature gradients,

which are present in the deforming material dur-

ing hot forming operations. As a result, the ef-

fect of temperatures on ﬂow stress and metal

ﬂow during hot forming are often not considered

adequately.

In the ﬁnite difference method, the deriv-

atives in the governing partial differential equa-

tions are written in terms of difference equa-

tions. Therefore, for a two-dimensional domain,

a grid of cells is placed inside the domain and

the differencing approximation applied to each

interior point. This results in a system of linear

algebraic equations (with a banded solution ma-

trix), which yields a unique solution provided

the boundary conditions of the actual problem

are satisﬁed. Though temperature gradients can

be taken into account, this method is limited to

problems with simple boundaries [Becker,

1992].

In the ﬁnite element method, the entire so-

lution domain is divided into small ﬁnite seg-

ments (hence, the name “ﬁnite elements”). Over

each element, the behavior is described by the

differential equations. All these small elements

are assembled together, and the requirements of

continuity and equilibrium are satisﬁed between

neighboring elements. Provided the boundary

conditions of the actual problem are satisﬁed, a

unique solution can be obtained to the overall

system of linear algebraic equations (with a

sparsely populated solution matrix) [Becker,

1992].

In recent years, the ﬁnite element method has

gained wide acceptance in the industry and ac-

ademia. This can be attributed to the rapid ad-

vancement in the computing technology, user-

friendly commercial FE software and the

detailed information FEM can provide as com-

pared to other methods of analysis. The FE

method allows the user to incorporate in the

simulation: (a) the tool and workpiece tempera-

tures, (b) the heat transfer during deformation,

strain hardening characteristics, and (e) capabil-

ities for microstructure analysis. This results in

a more accurate analysis of the forging process.

Commercial FE software packages have been

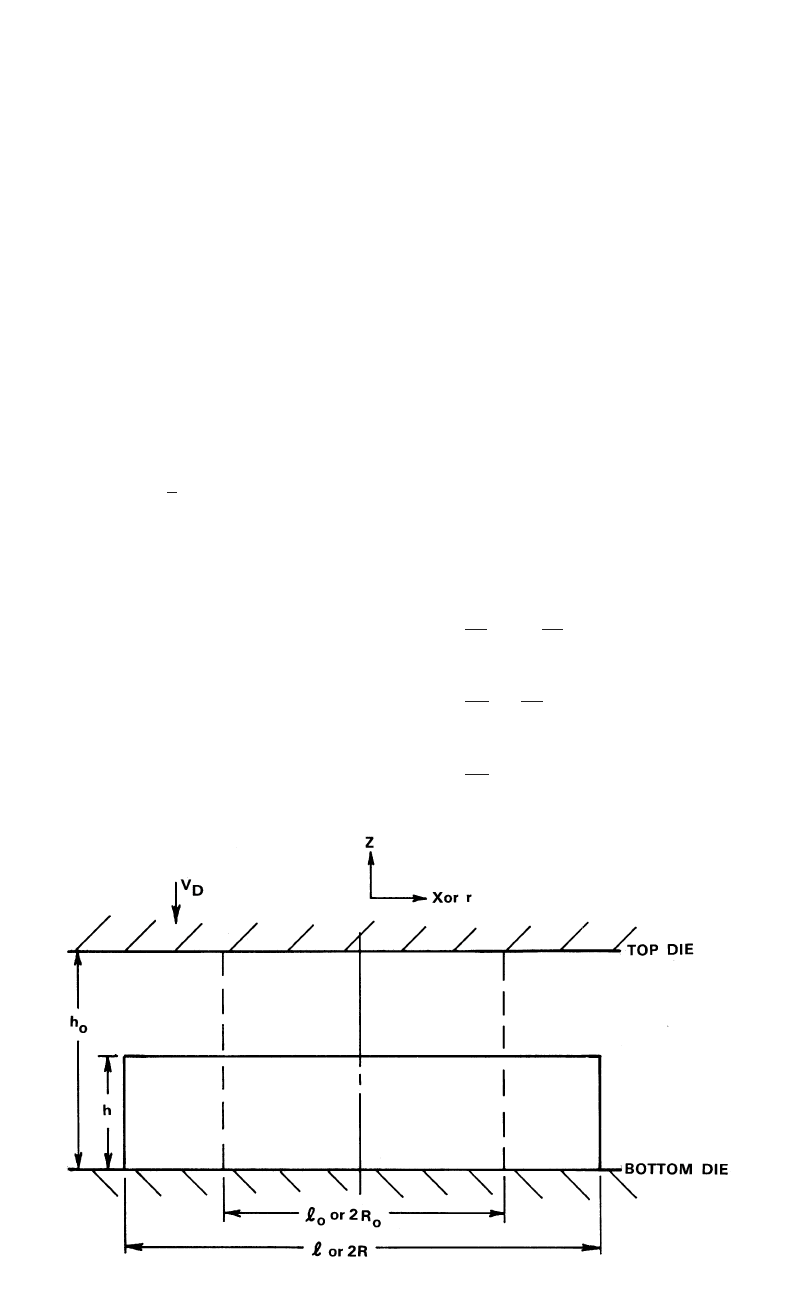
Methods of Analysis for Forging Operations / 93

Fig. 9.1 Changes in shape during upsetting. Plane strain (initial width ᐉ

and initial height h

) and axisymmetric (initial radius R

)

used successfully in simulating complex two-di-

mensional (2-D) and three-dimensional (3-D)

forging operations.

This chapter brieﬂy discusses the slab, upper-

bound, and the ﬁnite element (FE) methods.

9.2 Slab Method of Analysis

The following assumptions are made in using

the slab method of analysis:

●

The deforming material is isotropic and in-

compressible.

●

The elastic deformations of the deforming

material and the tool are neglected.

●

The inertial forces are small and are ne-

glected.

●

The frictional shear stress, s, is constant at

the die/material interface and is deﬁned as

s ⳱

f¯r ⳱ m¯r/3.

冪

●

The material ﬂows according to the von

Mises rule.

●

The ﬂow stress and the temperature are con-

stant within the analyzed portion of the de-

forming material.

The basic approach for the practical use of the

slab method is as follows:

1. Estimate or assume a velocity or metal ﬂow

ﬁeld.

2. For this velocity ﬁeld, estimate the average

strains, strain rates, and temperatures within

each distinct time zone of the velocity ﬁeld.

3. Thus, estimate an average value of the ﬂow

stress, within each distinct zone of de-¯r,

formation.

4. Knowing and friction, derive or apply the¯r

necessary equations for predicting the stress

distribution and the forming load (in the

slab method) or the forming load and the

average forming pressure (in the upper-

bound method).

9.2.1 Application of Slab

Method to Plane-Strain Upsetting

The Velocity Field. In this case, deformation

is homogeneous and takes place in the x-z plane

(Fig. 9.1). The velocity ﬁeld, with the velocities

in the x, y, and z directions, is deﬁned as:

v ⳱ⳮV z/h; v ⳱ V x/h; v ⳱ 0 (Eq 9.1)

zDxDy

where V

is the velocity of the top die.

The strain rates are:

⳵vV

˙e ⳱⳱ⳮ (Eq 9.2a)

⳵zh

⳵vV

˙e ⳱⳱⳱ⳮ˙e (Eq 9.2b)

⳵xh

⳵v

˙e ⳱⳱0 (Eq 9.2c)

⳵y

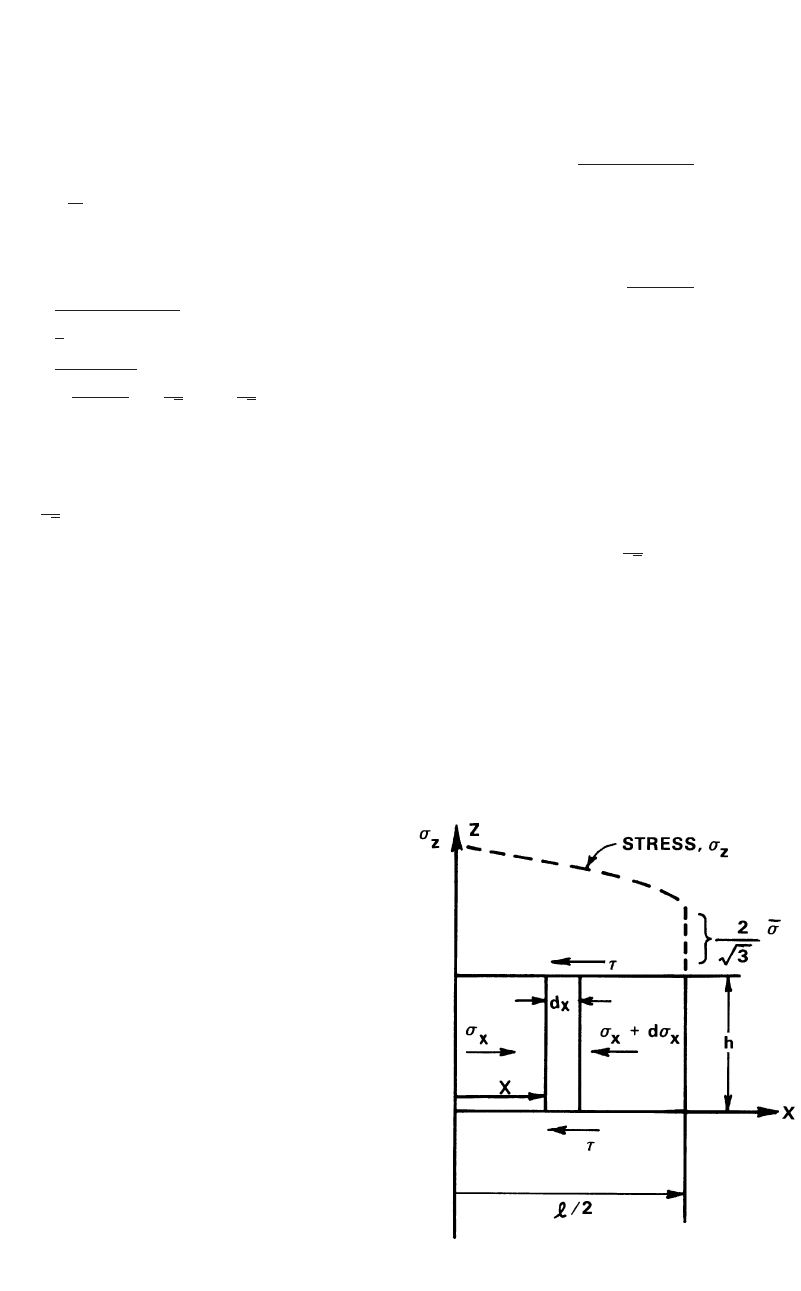
94 / Cold and Hot Forging: Fundamentals and Applications

Fig. 9.2

Equilibrium of forces in plane strain homogeneous

upsetting

It can be shown easily that the shear strain rates

are ⳱ 0.˙c ⳱ ˙c

xz yz

The strains are:

e ⳱ ln ; e ⳱ⳮe ; e ⳱ 0 (Eq 9.3)

zxzy

The effective strain rate is given by the equa-

tion:

222

¯e ⳱ (˙e Ⳮ ˙e Ⳮ ˙e )

xyz

冪

˙e Ⳮ ˙e 22

¯e ⳱ 2 ⳱ |˙e | ⳱ |˙e | (Eq 9.4)

冢冣

冪

冪冪

The effective strain is:

¯e ⳱ |e | (Eq 9.5)

冪

The slab method of analysis assumes that the

stresses in the metal ﬂow direction and in the

directions perpendicular to the metal ﬂow direc-

tion are principal stresses, i.e.:

r ⳱ r , r ⳱ r ; r ⳱ r (Eq 9.6)

z1x3y2

Plastic deformation/plastic ﬂow starts when

the stresses at a given point in the metal reach a

certain level, as speciﬁed by a ﬂow rule such as

the Tresca or von Mises rule discussed in Chap-

ter 5. Analysis of plastic deformation requires a

certain relationship between the applied stresses

and the velocity ﬁeld (kinematics as described

by velocity, strain (e) and strain rate ﬁelds).(˙e)

Such a relation between the stresses (in principal

axes) and strain rates is given as follows:

˙e ⳱ k(r ⳮ r )

11m

˙e ⳱ k(r ⳮ r )

22m

˙e ⳱ k(r ⳮ r )

33m

where k is a constant and r

is the hydrostatic

stress.

These equations are called the plasticity equa-

tions. From these equations, for the plane strain

case one obtains:

˙e ⳱ ˙e ⳱ k(r ⳮ r ) ⳱ 0

2y 2 m

r ⳱ r (Eq 9.7)

Per deﬁnition:

r Ⳮ r Ⳮ r

123

r ⳱

or, with Eq 9.7:

r Ⳮ r

r ⳱ r ⳱

For plane strain, i.e., r

⳱ r

, the von Mises

rule gives:

222

3[(r ⳮ r ) Ⳮ (r ⳮ r ) ⳮ 0] ⳱ 2¯r

1m 3m

(Eq 9.8)

After simpliﬁcation, the ﬂow rule is:

2¯r

r ⳮ r ⳱ r ⳮ r ⳱ (Eq 9.9)

13zx

冷冷

冪

Estimation of Stress Distribution. In apply-

ing slab analysis to plane strain upsetting, a slab

of inﬁnitesimal thickness is selected perpendic-

ular to the direction of metal ﬂow (Fig. 9.2).

Assuming a depth of “1” or unit length, a force

balance is made on this slab. Thus, a simple

equation of static equilibrium is obtained

[Thomsen et al., 1965] [Hoffman et al., 1953].

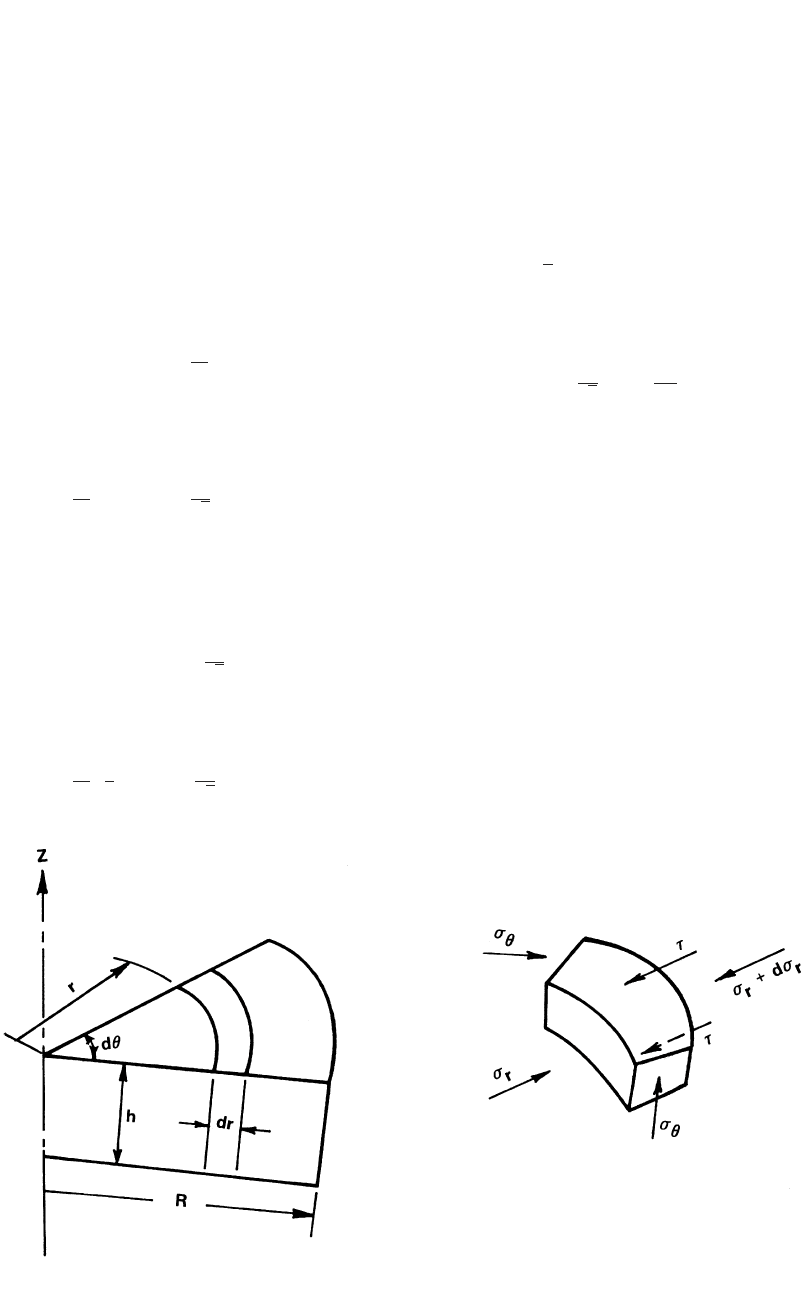
Methods of Analysis for Forging Operations / 95

Fig. 9.3 Equilibrium of forces in axisymmetric homogeneous upsetting

Summation of forces in the X direction is zero

or:

F ⳱ r h ⳮ (r Ⳮ dr )h ⳮ 2sdx ⳱ 0

兺

xx x x

dr ⳱ⳮ2sdx/h

Thus, by integration one gets:

r ⳱ⳮ x Ⳮ C

From the ﬂow rule of plane strain, it follows

that:

2s 2

r ⳱ⳮ x Ⳮ C Ⳮ ¯r (Eq 9.10)

冷冷

冪

The constant C is determined from the boundary

condition at x ⳱ ᐉ/2, where r

⳱ 0, and, from

Eq 9.9:

r ⳱ ¯r

冷冷

冪

Thus:

2s ᐉ 2

r ⳱ⳮ ⳮx ⳮ ¯r (Eq 9.11)

冢冣

冪

Equation 9.11 illustrates that the vertical

stress increases linearly from the edge (x ⳱

ᐉ/2) of Fig. 9.2 toward the center (x ⳱ 0). The

value of r

is negative, because z is considered

to be positive acting upward and the upsetting

stress is acting downward. Integration of Eq

9.11 gives the upsetting load.

In Eq 9.11, the frictional shear stress, s,is

equal to Thus, integration of Eq 9.11

m¯r/3.

冪

over the entire width, ᐉ, of the strip of unit depth

gives the upsetting load per unit depth:

2¯r mᐉ

L ⳱ 1 Ⳮ ᐉ

冢冣

冪

9.2.2 Application of the Slab Analysis

Method to Axisymmetric Upsetting

Figure 9.3 illustrates the notations used in the

homogeneous axisymmetric upsetting. The anal-

ysis procedure is similar to that used in plane

strain upsetting.

Velocity Field. The volume constancy holds;

i.e., the volume of the material moved in the z

direction is equal to that moved in the radial di-

rection, or:

prV ⳱ 2prv h, or v ⳱ V r/2h

DrrD

In the z direction, v

can be considered to vary

linearly while satisfying the boundary condi-

tions at z ⳱ 0 and z ⳱ h. In the tangential di-

96 / Cold and Hot Forging: Fundamentals and Applications

rection, H, there is no metal ﬂow. Thus, the ve-

locities are:

v ⳱ V r/2h; v ⳱ⳮV z/h; v ⳱ 0 (Eq 9.13)

rD z D H

In order to obtain the strain rate in the tan-

gential direction, it is necessary to consider the

actual metal ﬂow since v

⳱ 0 and cannot be

used for taking a partial derivative. Following

Fig. 9.3, the increase in strain in the H direction,

i.e., the length of the arc, is given by:

(r Ⳮ dr)dH ⳮ rdH dr

de ⳱⳱(Eq 9.14)

rdH r

or the strain rate is

de dr 1 v V

H rD

˙e ⳱⳱ ⳱⳱ (Eq 9.14a)

dt dt r r 2h

The other strain rates are:

⳵vV

˙e ⳱⳱ⳮ (Eq 9.14b)

⳵zh

⳵vV

˙e ⳱⳱⳱˙e (Eq 9.14c)

r H

⳵r2h

1 ⳵v ⳵v

˙c ⳱Ⳮ⳱0 (Eq 9.14d)

冢冣

2 ⳵z ⳵r

˙c ⳱ ˙c ⳱ 0 (Eq 9.14e)

HzrH

Thus, the effective strain rate is:

222

¯e ⳱ (˙e Ⳮ ˙e Ⳮ ˙e ) ⳱ |˙e | (Eq 9.15)

H rz z

冪

The strains can be obtained by integrating the

strain rates with respect to time, i.e.:

Vdt

e ⳱ ˙e dt ⳱ⳮ

冮冮

or with ⳮdh ⳱ⳮV

dt:

dh h

e ⳱ⳮ⳱ⳮln (Eq 9.16a)

冮

Similarly, the other strains can be obtained as:

1h e

e ⳱ e ⳱ ln ⳱ⳮ (Eq 9.16b)

H r

2h 2

In analogy with Eq 9.15, the effective strain is:

¯e ⳱ |e | (Eq 9.17)

The ﬂow rule for axisymmetric deformation

is obtained by using a derivation similar to that

used in plane strain deformation. Because

, the plasticity equations give:˙e ⳱ ˙e

r h

r ⳱ r or r ⳱ r

r h 23

Thus, the von Mises ﬂow rule for axisymmetric

upsetting is:

r ⳮ r ⳱ |¯r|orr ⳮ r ⳱ |¯r| (Eq 9.18)

12 zr

Estimation of Stress Distribution. The equi-

librium of forces in the r direction (Fig. 9.3)

gives [Thomsen et al., 1965] [Hoffman et al.,

1953]:

F ⳱ r (dh)rh ⳮ (r Ⳮ dr )

兺

rr r r

(r Ⳮ dr)hdh Ⳮ 2r sin

hdr ⳮ 2srdhdr ⳱ 0 (Eq 9.19)

The angle dh is very small. Thus, with sin dh/2

⳱ dh/2, and after canceling appropriate terms,

Eq 9.19 reduces to:

dr 2s

ⳮr ⳮ r Ⳮ r ⳮ r ⳱ 0 (Eq 9.20)

r h

dr h

Since in axisymmetric deformation, ˙e ⳱ ˙e ,

r h

the plasticity equations give:

dr 2s

r ⳱ r ,or Ⳮ⳱0 (Eq 9.21)

r h

dr h

Integration gives:

r ⳱ⳮ r Ⳮ C

The constant C is determined from the condition

that at the free boundary, r ⳱ R in Fig. 9.3, and

the radial stress r

⳱ 0. Thus, integration of Eq

9.21 gives:

r ⳱ (r ⳮ R) (Eq 9.22)

Methods of Analysis for Forging Operations / 97

With the ﬂow rule, Eq 9.22 is transformed

into:

r ⳱ (r ⳮ R) ⳮ ¯r (Eq 9.23)

Equation 9.23 illustrates that the stress increases

linearly from the edge toward the center. The

upsetting load can now be obtained by integrat-

ing the stress distribution over the circular sur-

face of the cylindrical upset:

L ⳱ r 2prdr

冮

Considering that s ⳱ integration gives:m¯r/3,

冪

2mR

L ⳱ ¯rpR1Ⳮ (Eq 9.24)

冢冣

3h 3

冪

9.3 Upper Bound Method and

Its Application to

Axisymmetric Upsetting

9.3.1 Principles of the Method

This method can be used to estimate the de-

formation load and the average forming pres-

sure. For describing metal ﬂow with the upper-

bound method, it is necessary to make the usual

assumptions, discussed earlier in the slab

method, as well as perform the following steps:

1. Describe a family of admissible velocity

ﬁelds (use parameters to be determined later);

these must satisfy the conditions of: incom-

pressibility, continuity, and velocity bound-

aries.

2. Calculate the energy rates of deformation, in-

ternal shear, and friction shear.

3. Calculate the total energy rate and minimize

it with respect to unknown parameters of ve-

locity ﬁeld formulation.

The load is then obtained by dividing the energy

rate by the relative velocity between the die and

the deforming material.

The total energy rate, E

, is given by E

⳱

load ⳯ die velocity, or [Avitzur, 1968]:

˙˙˙˙

E ⳱ LV ⳱ E Ⳮ E Ⳮ E

TDDSF

E ⳱ ¯r ¯edV Ⳮ s|Dv|ds Ⳮ s vds

Tii

冮冮冮

VSS SF

(Eq 9.25)

where E

, and E

are the energy rates for

deformation, internal shear, and friction, respec-

tively; L is the forming load; V is the volume of

deforming material; v is the relative velocity be-

tween two zones of material, when the velocity

ﬁeld has internal shear surfaces; S indicates sur-

face (internal or at die/material interface); v

the die material interface velocity in the “i” por-

tion of the deforming material; s ⳱ and

¯r/3;

冪

⳱⳱interface shear stress at the “i”m¯r/3

冪

portion of the deforming material.

Based on limit theorems [Avitzur, 1968], the

load calculated with Eq 9.25 is necessarily

higher than the actual load and therefore repre-

sents an upper bound to the actual forming load.

Thus, the lower this upper bound load is, the

better the prediction. Often the velocity ﬁeld

considered includes one or more parameters that

are determined by minimizing the total energy

rate with respect to those parameters. Thus, a

somewhat better upper-bound velocity ﬁeld and

solution are obtained. In general, with an in-

creasing number of parameters in the velocity

ﬁeld, the solution improves while the computa-

tions become more complex. Consequently, in

the practical use of the upper-bound method,

practical compromises are made in selecting an

admissible velocity ﬁeld.

9.3.2 Application to Axisymmetric

Homogeneous Upsetting

The velocity ﬁeld for homogeneous upsetting

is given by Eq 9.13 to 9.15. Thus, all the veloc-

ities and strain rates are known. Assuming a con-

stant ﬂow stress, the deformation energy rate¯r,

is:

E ⳱ ¯r ¯edV ⳱ hpR¯r (Eq 9.26)

冮

(internal shear energy rate) ⳱ 0, because

there are no internal velocity discontinuities in

the present homogeneous velocity ﬁeld.

The friction energy rate is:

E ⳱ 2 s vds

Fii

冮

where v

is the radial velocity, given in Eq 9.13,

and ds ⳱ 2prdr. E

includes the friction energies