Dantzig G., Thapa M. Linear programming. Vol.1. Introduction

Подождите немного. Документ загружается.

82 THE SIMPLEX METHOD

where

≥ 0 and ¯w

= 0, since feasible solutions exist. For feasibility, w must

remain zero in Phase II, which means that every x

corresponding to

> 0

must be zero; hence, all such x

can be set equal to zero and dropped from

further consideration in Phase II. We can also drop any nonbasic artiﬁcials as

no longer of any interest. Our attention is now conﬁned only to variables whose

corresponding

= 0. All feasible solutions involving only these remaining

variables now have w = 0 by (3.40), and therefore the remaining artiﬁcial

variables that sum to w are also zero and will remain zero as we subsequently

pivot. Consequently, the feasible solution to the modiﬁed augmented problem

is also a feasible solution for the original problem.

A variant of this method is to treat the z-equation as just another constraint

with z unrestricted in sign during Phase I. This automatically eliminates the

basic variables x

from the z-equation on each iteration. It does not require

any manipulation of data structures; but it can involve more computations.

2. A second way to maintain the basic artiﬁcial variables at zero values during

Phase II is to try to eliminate (if possible) all artiﬁcial variables still in the

basic set. This can be done by choosing a pivot in a row r corresponding to

such an artiﬁcial variable and in any column s ≤ n such that ¯a

= 0. If all

coeﬃcients in such a row for j =1,...,n are zero, the row may be deleted

because the corresponding equation in the original system is redundant, or

the row may be left in if that is more convenient.

3. A third way is to keep the w equation during Phase II and treat the (−w)

variable as just another variable that is restricted to nonnegative values. The

system is then augmented by introducing the z-equation after eliminating the

basic variables from it. Since w ≥ 0 is always true, the added condition

(−w) ≥ 0 implies w = 0 during Phase II.

 Exercise 3.15 Solve the following problem by all three ways of transitioning from

Phase I to Phase II. Find max z, x ≥ 0 such that

10x

+10x

+20x

+30x

= z

+ x

+2x

+ x

=7.

(3.41)

Replace the last constraint by 3x

+2x

+5x

= 7 and solve the problem again using

all three ways of transitioning from Phase I to Phase II. Explain what properties these

two examples have that make them interesting.

THEOREM 3.8 (Artiﬁcial Variables in Phase II) If artiﬁcial variables

form part of the basic sets of variables in the various iterations of Phase II, their

values will never exceed zero.

Proof. The proof follows from the discussion of the ﬁrst way to maintain artiﬁcial

variables at zero in Phase II.

3.4 BOUNDED VARIABLES 83

 Exercise 3.16 Prove that the second way to maintain artiﬁcial variables at zero values

is valid.

 Exercise 3.17 Suppose Phase I terminates with a feasible solution with k artiﬁcials in

the basis. Show that if we know in advance that there are no degenerate solutions after the

removal of all redundant equations, then k is equal to the number of redundant equations.

 Exercise 3.18 Suppose at the end of Phase I that one or more artiﬁcial variables

remain in the basis at zero level. Assume that we can initiate Phase II by setting the cost

coeﬃcients c

of all the artiﬁcials in the z equation at zero. Show that, as the iterations of

the Simplex Algorithm are performed, we can ensure that the artiﬁcial variables remain

at zero by the following procedure.

1. If for the incoming column s, we have one or more ¯a

≥ 0 for i corresponding to an

artiﬁcial variable, we perform the usual minimum ratio test.

2. On the other hand, if for all i corresponding to artiﬁcial variables we have ¯a

≤ 0,

then instead of performing the minimum ratio test, we pivot on any r = i corre-

sponding to an artiﬁcial variable.

3.4 BOUNDED VARIABLES

We now turn our attention to solving a linear program in bounded variables, that

is,

Minimize c

subject to Ax = b, A : m ×n,

l ≤ x ≤ u.

(3.42)

As earlier, the independent variables will correspond to nonbasic variables, x

, and

the dependent ones to basics, x

. Let the canonical form with respect to x

be as

before:

(−z)+0x

+¯c

= −¯z

(3.43)

where subscript B (or B) is the set of indices of basic variables, and subscript N

(or N) is the set of indices of the nonbasic variables.

Deﬁnition (Basic Solution): Assuming that at least one of the bounds for

each x

is ﬁnite, the special solution obtained by setting each nonbasic equal

to either its lower bound or upper bound and then solving for the values of

the basic variables will now be called a basic solution.

Deﬁnition (Degenerate Solution): A basic solution is degenerate if the values

of one or more of the basic variables in the basic solution are at either their

lower bound or upper bound.

84 THE SIMPLEX METHOD

 Exercise 3.19 Assume that for some j = j

, x

in (3.42) has a lower bound of −∞

and an upper bound of +∞. Further assume that the lower bounds on all other variables

are ﬁnite. Show how to convert such a problem into one where at least one of the bounds

on each variable is ﬁnite by each of the following three ways:

1. By eliminating the variable x

2. By replacing x

by the diﬀerence of two nonnegative variables.

3. By making sure that the variable x

is basic on the ﬁrst iteration of Phase I and

then never making it nonbasic thereafter.

Explain why method 3 is the same as method 1.

 Exercise 3.20 Show that for problem (3.42) if each upper bound and lower bound is

ﬁnite, then the linear program can never have an unbounded solution.

 Exercise 3.21 Let x

=(x

) be a basic solution as deﬁned above. Assume that the

lower and upper bounds for each x

are ﬁnite. Make the following transformation:

1. If x

= u

, replace x

by u

− y

2. If x

= l

, replace x

by l

+ y

3. If l

, replace x

by y

Show that y

is a basic solution as deﬁned earlier on Page 66.

THEOREM 3.9 (Optimality Test for the Bounded Variable LP) Let

x =(x

∗

) be a basic solution to (3.43) according to the above deﬁnition, i.e.,

∗

b −

∗

and each nonbasic component of x

∗

, for j ∈N, must satisfy x

∗

= l

or x

∗

= u

. Then (x

∗

) is a minimal solution with total costs z

∗

=¯z

+¯c

∗

≤ x

∗

b −

∗

≤ u

, (a)

¯c

≥ 0 for j ∈L, (b)

¯c

≤ 0 for j ∈U, (c)

(3.44)

where

L = {j ∈N|x

∗

= l

U = {j ∈N|x

∗

= u

(3.45)

Proof. Clearly, for the basic solution to be feasible (3.44a) must hold. The

objective function value is given by

∗

=¯z

+¯c

∗

=¯z



j∈L

¯c

∗



j∈U

¯c

∗

. (3.46)

For any feasible (x, z), we have

z =¯z



j∈L

¯c



j∈U

¯c

. (3.47)

3.4 BOUNDED VARIABLES 85

Clearly, if ¯c

≥ 0 for j ∈L, then the best we can do is to have the corresponding

be at their lower bounds, x

∗

= l

. Similarly, if ¯c

≤ 0 for j ∈U, then the

best we can do is to have the corresponding x

be at their upper bounds, x

∗

= u

Thus, the right-hand side of (3.46) is a lower bound for z. Since this lower bound

is attained for the basic feasible solution (x

∗

), the minimum value of z in (3.47)

is the minimum value of z attained for all feasible solutions, basic or otherwise.

MODIFYING THE SIMPLEX ALGORITHM TO SOLVE THE

BOUNDED VARIABLE PROBLEM

To see how to modify the Simplex Algorithm to solve the bounded variable LP, note

the following:

1. The optimality conditions for a basic feasible solution x =(x

) are

¯c

≥ 0 for j ∈L,

¯c

≤ 0 for j ∈U.

(We are assuming, to simplify the discussion, that at least one bound on

each x

is ﬁnite.) If the optimality conditions are not satisﬁed, the incoming

variable is selected by ﬁnding the index j = s such that

s = argmin

{

j∈L}

{k∈U}

{¯c

, −¯c

}. (3.48)

2. If not optimal, we try to bring the nonbasic variable with index j = s into the

basis. Clearly if x

= u

, we will try to decrease x

, and if x

= l

, we will try

to increase x

in an attempt to bring it into the basis. Let δ be deﬁned by

δ =



1ifx

= l

−1ifx

= u

(3.49)

The nonbasic variable x

will change as follows:

= x

+ δθ, (3.50)

where θ ≥ 0 will be determined as shown below so that x

and the basic

variables x

, for i =1,...,m, all stay within their bounds.

This implies that we must have l

≤ x

+ δθ ≤ u

and l

≤ x

− δθ¯a

≤ u

for i =1,...,m. The other nonbasic variables are ﬁxed at x

= x

. From this

it follows that θ is the smallest of three ratios

= u

− l

, (3.51)

= min

{i|δ ¯a

>0}



− l

δ ¯a

, ∞



≥ 0, (3.52)

= min

{i|δ ¯a

<0}



− x

−δ ¯a

, ∞



≥ 0, (3.53)

86 THE SIMPLEX METHOD

where δ is deﬁned in equation (3.49). Note that θ

is the maximum amount

that x

can change given its upper and lower bounds; θ

reﬂects the maximum

that x

can change before one of the lower bounds on a basic variable is

violated; and θ

reﬂects the maximum that x

can change before one of the

upper bounds on a basic variable is violated. Let

r = argmin(θ

,θ

It may happen that θ = θ

, in which case there is no change to the basis—the

nonbasic variable x

simply switches bounds and causes a feasible change in

the values of the basic variables. The case r = s occurs often in practice

and requires less work because there is no change to the basis, and hence no

pivoting is required.

3. The current value of x

changes as follows:

= x

− δθ

•s

, (3.54)

where δ is given by (3.49).

 Exercise 3.22 Compare the steps of the algorithm just described for the bounded

variable problem, when the lower bounds l are equal to 0 and upper bounds u are equal to

∞, with the standard Simplex Algorithm 3.1 and show that the steps just discussed are

identical.

 Exercise 3.23 Write down the complete Simplex Algorithm for solving a linear program

with bounded variables.

Example 3.2 (Solving a Linear Program with Bounded Variables) This example

illustrates the use of the Simplex Algorithm as modiﬁed for a bounded variable linear

program.

Minimize −3x

− 2x

= z

subject to 2x

+ x

≤ 10

+3x

≤ 27

0 ≤ x

≤ 4, 0 ≤ x

≤ 5.

(3.55)

We add slacks x

and x

and set each of their lower bounds to 0 and upper bounds to +∞.

In this case we obtain an initial starting solution by setting x

and x

to their lower bounds

of 0 and solving for the slack basic variables x

and x

. In general, we may not be so lucky

and may need to add artiﬁcial variables (and also possibly change signs of the equations).

At the start of iteration 0, the initial tableau is shown under iteration 0 in Table 3-3.

Note that for nonbasic j the last row displays the bound status; if nonbasic j is at its lower

bound the status is l, otherwise the status is u.

Notice that both x

and x

are at their lower bound with ¯c

= −3 and ¯c

= −2

(displayed in the z row). Therefore, by (3.48), s = 1. Thus, we should try to increase

= x

since it is at its lower bound. Applying (3.51)–(3.53), the three ratios are θ

=4,

= 5, and θ

=+∞, implying r = s = 1. Hence by the end of the initial iteration, x

has moved to its upper bound and remains nonbasic; since θ = θ

, the basis is unchanged

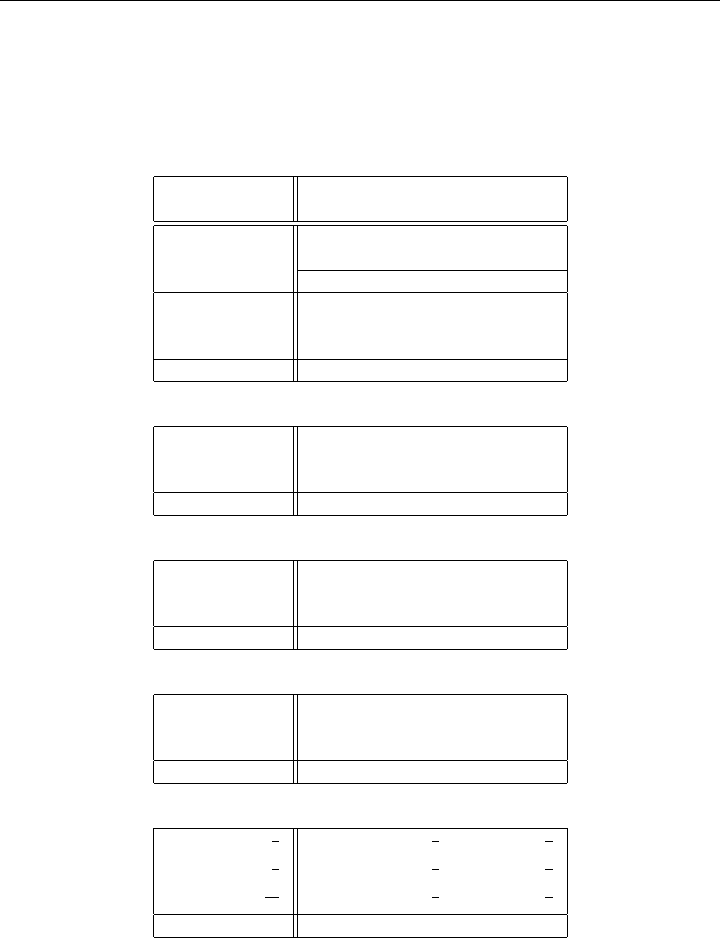
3.4 BOUNDED VARIABLES 87

Iteration 0 (Phase II)

Lower Bound −∞ 0000

Upper Bound +∞ 45+∞ +∞

Basic

Variables Variables

−zx

−z =0 1 −3 −200

=10 2110

=27 5301

Status ll

Iteration 1 (Phase II)

−z =12 1 −3 −200

=2 2 1 10

=7 5301

Status ul

Iteration 2 (Phase II)

−z =16 11020

=2 2110

=1 −1 0 −31

Status ul

Iteration 3 (Phase II)

−z =17 100−11

=4 01−5 2

=3 10 3−1

Status ll

Iteration 4 (Phase II)

−z =17

10−

0 −

1 −

Status ul

Table 3-3: Tableau Form Example of a Bounded Variable LP

88 THE SIMPLEX METHOD

and no pivoting is required. However, the new basic values for the basic variables need to

be computed by (3.54):



−z







− 4 ×



−3







At the start of iteration 1, x

is at its upper bound and x

is at its lower bound, with

¯c

= −3 and ¯c

= −2, and therefore by (3.48), s = 2. Thus, we should try to increase

= x

since it is at its lower bound. Applying (3.51)–(3.53), the three ratios are θ

=5,

= 2, and θ

=+∞, implying r = l = 1, where j

= j

= 3. Hence, x

= x

enters the

basis at value x

= θ = 2, and x

leaves the basis to be at its lower bound. We compute

the change of basic variables x

and x

= x

by (3.54) and (3.50) respectively:



−z







− 2 ×



−2







= l

+ δθ =0+2=2, replacing x

in the basis.

The values of (−z), x

, and x

are posted to the left of the double line at the start of

iteration 2. Next we pivot on the boldface term 1 and record the resulting values in the

tableau for the start of iteration 2.

At the start of iteration 2, x

is at its upper bound and x

is at its lower bound, with

¯c

= 1 and ¯c

= 2. Therefore by (3.48), s = 1. Thus, we should try to decrease x

= x

since it is at its upper bound; in this case δ = −1. Applying (3.51)–(3.53), the three ratios

are θ

=4,θ

= 1, and θ

=3/2, implying r = l = 2, where j

= j

= 4. Hence, x

= x

enters the basis at value x

= u

− θ = 3, and x

leaves the basis at its lower bound. We

compute the change of basic variables x

and x

= x

by (3.54) and (3.50) respectively:



−z







− (−1) × 1 ×



−1







= u

+ δθ =4+(−1) × 1=3, replacing x

in the basis.

The values of (−z), x

, and x

are posted to the left of the double line at the start of

iteration 3. Next we pivot on the boldface term −1 and record the resulting values in the

tableau for the start of iteration 3.

At the start of iteration 3, x

is at its lower bound and x

is also at its lower bound, with

¯c

= −1 and ¯c

= 1. Therefore by (3.48), s = 3. Thus, we should try to increase x

= x

since it is at its lower bound. Applying (3.51)–(3.53), the three ratios are θ

=+∞, θ

=1,

and θ

=1/5, implying r = u = 1, where j

= j

= 2. Hence, x

= x

enters the basis

at value x

= l

+ θ =1/5, and x

leaves the basis at its upper bound. We compute the

change of basic variables x

and x

= x

by (3.54) and (3.50) respectively:



−z







−



−1

−5







= l

+ δθ =0+1/5=1/5, replacing x

in the basis.

3.5 REVISED SIMPLEX METHOD 89

The values of (−z), x

, and x

are posted to the left of the double line at the start of

iteration 4. Next we pivot on the boldface term −5 and record the resulting values in the

tableau for the start of iteration 4.

At the start of iteration 4, the tableau is optimal by Theorem 3.9, since x

is at its

upper bound and ¯c

is negative; and, x

is at its lower bound and ¯c

is positive. The

optimal solution is readily read oﬀ from the tableau: The basic values are z = −17

=1/5, and x

=12/5; the nonbasic values are x

= 5 since x

has status u, and x

since x

has status l.

3.5 REVISED SIMPLEX METHOD

The Revised Simplex Method is not a diﬀerent method but is a diﬀerent way to

carry out each computational step of the Simplex Method. The revised method

oﬀers several advantages over the Simplex Algorithm in tableau form.

1. Considerable savings in computations are possible if the fraction of nonzero

coeﬃcients is less than 1 − (2m/n). This is typically the case in practice.

2. Less data is recorded from one iteration to the next, which permits a larger

problem to be solved when the memory capacity of an electronic computer

is limited. Furthermore, considerable savings in computations are possible

because not all the entries in the tableau need to be updated.

3. A weakness of the simplex algorithm in tableau form is that the inverse of the

basis in explicit form is part of the full tableau. The explicit representation

of the inverse can be numerically unstable. Since the inverse is only needed

to solve certain systems of equations, the need to have an inverse can be

bypassed in the Revised Simplex Algorithm by solving the system of equations

by numerically stable methods.

3.5.1 MOTIVATION

While each iteration of the Simplex Method requires that a whole new tableau be

computed and recorded, it may be observed that only the modiﬁed cost row and

the column corresponding to the variable entering the basic set play any role in the

decision process. That is, in order to carry out the steps of the Simplex Algorithm

(see Algorithm 3.1),

1. we ﬁrst look at the reduced costs (¯c ) to determine whether an improvement

in the solution is possible, and if so, then we determine which column s to

bring into the basis (see Steps 1–3 of the Simplex Algorithm);

2. next we look at the pivot column

•s

and the right hand side

b to determine

the pivot row r and the variable that leaves the basis (see Steps 4–5 of the

Simplex Algorithm).

90 THE SIMPLEX METHOD

Since

b can be easily updated, at each iteration all we need are the reduced costs

and the updated column corresponding to the incoming variable. It turns out that

we can obtain this information directly if we have available a way to solve a system

of equations whose coeﬃcient matrix is the current basis matrix B or its transpose.

Any eﬃcient way to update the solution procedures for the next iteration will do.

For the purpose of illustrating the Revised Simplex Algorithm on small examples,

we will use an explicit representation of B

−1

and a way to update it. In general, as

we have just noted, computing and using an inverse can be a numerically unstable

process and also, for large problems an explicit representation of B

−1

may not be

computationally eﬃcient in terms of speed and storage.

If we have at hand an explicit representation of B

−1

, it is easy to derive the

required quantities ¯c and

•s

from the original data. Assume that an initial feasible

solution is available for a given linear program in standard form (3.1). Suppose, for

convenience of discussion, that the columns of the coeﬃcient matrix A have been

ordered so that the basis columns (represented by the matrix B = B

for iteration

t) are the ﬁrst m columns of A and the nonbasic columns (represented by the matrix

N = N

) are the last (n − m) columns of A. That is,

(−z)+c

+ c

=0 (a)

+ Nx

= b (b).

(3.56)

Algebraically, the canonical form of (3.56) for iteration t is given by

(−z)+(c

− c

−1

N)x

= −c

−1

b (a)

+ B

−1

= B

−1

b. (b)

(3.57)

This can be seen by multiplying (3.56b) by B

−1

on the left to obtain (3.57b). If now

we multiply (3.57b) on the left by c

and subtract from (3.56a), we obtain (3.57a).

But this is not the best way to carry out the computations.

To compute ¯c eﬃciently we ﬁrst compute

= c

−1

, (3.58)

and then

¯c

= c

− π

N, (3.59)

followed by s = argmin

¯c

. Then if ¯c

< 0, we compute

•s

= B

−1

•s

. (3.60)

The value

b = B

−1

b is not explicitly computed; instead it is updated in the Revised

Simplex Tableau when a pivot is performed.

Deﬁnition (Price): The vector π is called the price vector (or simplex multi-

pliers). We will see in Section 7.1 why the economists refer to π as the price

vector.

3.5 REVISED SIMPLEX METHOD 91

THEOREM 3.10 (Uniqueness of π) At any iteration t, the simplex multipliers

π are unique.

 Exercise 3.24 Prove Theorem 3.10.

Deﬁnition (Pricing Out): The operation of multiplying π times the nonbasic

column A

•j

for nonbasic j in the determination of N

π is called pricing out

the columns j.

Deﬁnition (Representation in Terms of the Basis): The linear combination

of the columns in the basis that yields the incoming column A

•s

is called the

representation of the sth activity in terms of the basic set of activities.Itis

easy to see that this representation is the updated column A

•s

, see (3.60),

because in matrix notation (3.60) can be rewritten as:

•s

= A

•s

. (3.61)

See Section A.6 in Appendix A where the notion of a basis in a vector space

is discussed.

Both pricing out a column and representation of an activity in terms of a basis

can be done very eﬃciently for matrices having many zero elements (so called sparse

matrices).

Next we shall show how to easily ﬁnd B

−1

and π in the tableau form. For

convenience of discussion we reorder the variables as before in (3.56) so that the

ﬁrst m columns of A are B = B

. Assume also that now we add m artiﬁcial

variables x

to (3.56b) to obtain (3.62):

(−z)+c

+ c

=0 (a)

+ Nx

+ Ix

= b. (b)

(3.62)

Once again multiplying (3.62b) by B

−1

, we get (3.63b), and subtracting the product

of c

times (3.63b) from (3.62a), we get (3.63a), which together give the canonical

form for iteration t:

(−z)+(c

− c

−1

N)x

− c

−1

= −c

−1

b (a)

+ B

−1

+ B

−1

= B

−1

b. (b)

(3.63)

Thus, π

= c

−1

and B

−1

for any iteration t can be directly read oﬀ from the

tableau by examining the columns corresponding to x

Furthermore, if we were to change the basis by pivoting in a new column from

A = B

−1

N, then the new basis inverse, say

−1

, would still be available in the

columns corresponding to x

 Exercise 3.25 Prove that no matter which column we bring into the basis, the new

basis inverse will be available in the columns corresponding to x